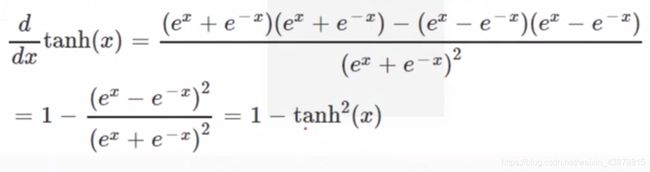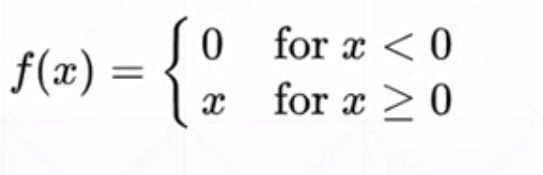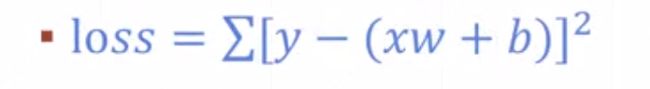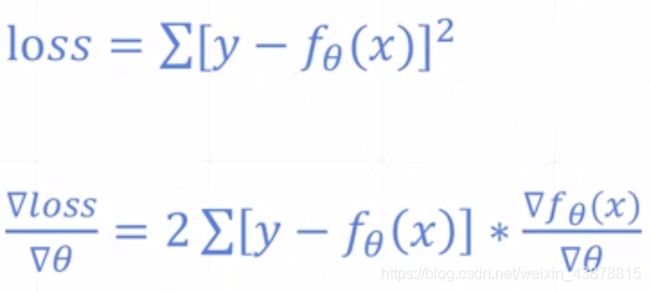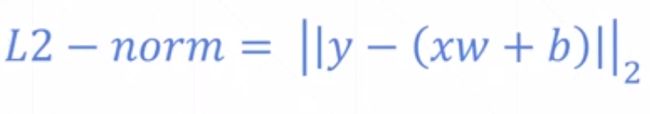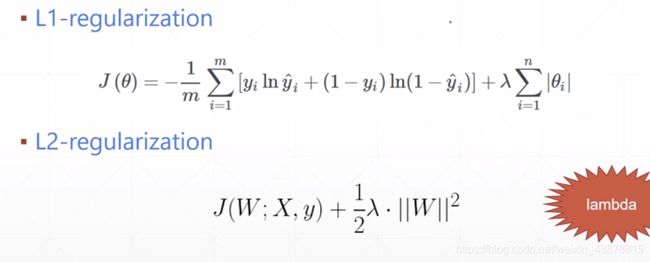深度学习记录
一、 Pytorch学习
1.Pytorch的安装
2.Pytorch的基本操作
3.Pytorch与其他框架的基本对比与优势
4.Pytorch的第一个小例子
5.回归问题
一、线性回归
提出问题:y = wx+b
如何根据不同的x和y的值不断的拟合数据集,找到一个比较合适的w和b参数,由此w和b构成的函数能够代表此数据集。为什么是拟合而不是直接求出精确解,是因为给定的数据有噪声。
y = w ∗ x + b + ϵ y = w*x+b+ \epsilon y=w∗x+b+ϵ
所以消元法不能够解决这个问题。
建立模型:给定自变量x,y求解w和b的值。wx+b-y=0 只要给定不同的x,y值就能解出次方程。但是存在噪声,只能求出一个近似值。所以构造loss函数,当loss最小时对应的w和b的值就更有代表性。
损失函数:用来判断拟合的好坏。当损失函数为零时证明找到w和b。但是实际应用中损失函数达不到零。括号内是预计值与实际值的差。
l o s s = ∑ ( w x i + b − y i ) 2 loss = ∑ (w x_{i}+b- y_{i}) ^{2} loss=∑(wxi+b−yi)2
解决问题:将问题转换为求loss函数最小值的问题。
二、分类问题
提出问题:如何解决手写数字的识别问题
建立模型:
训练集:
p r e d = f ( W 3 ∗ [ σ ( W 2 ∗ [ σ ( W 1 X + b 1 ) ] + b 2 ) ] + b 3 ) pred =f ( W_{3}*[\sigma (W_{2} *[\sigma ( W_{1}X+ b_{1})]+b_{2})]+b_{3}) pred=f(W3∗[σ(W2∗[σ(W1X+b1)]+b2)]+b3)
o b j e c t i v e = ∑ ( p r e d − Y ) 2 objective = ∑ (pred-Y )^{2} objective=∑(pred−Y)2
其中sigma为函数ReLU
真实值函数:Y:[0/1/2…/9]采用one-hot编码
解决问题:objective越小就说明越仅仅值,所以最小化objective函数。求出W和b的值。
测试集:
三、torch中的数据类型张量
1.dim=1
常用于Bias,linear input
in: torch.tensor([1.1])#.tensor接收的数据内容
Out: tensor([1.1000]) #默认补零小数点后4位
in: torch.FloatTensor(1)#.FloatTensor接收的是数据类型 初始化数据时是随机的
out:tensor([2.5715e-37])
in :torch.FloatTensor(2) #生成一个dim=1,size=2的张量 初始化时是随机的
out:tensor([3.4640e-37, 0.0000e+00])
in:data = np.ones(2)#numpy创建数据vector
in:data
out:array([1., 1.])
in:torch.from_numpy(data)#numpy类型转化为Tensor类型
out:tensor([1., 1.], dtype=torch.float64)
dim =2
用于linear input batch
in:a=torch.randn(2,3)#和FloatTensor方法是一样的 随机正态分布
in:a
out:tensor([[-1.5959, 1.0698, 1.2034],
[ 0.3786, 0.4144, 0.0969]])
in:torch.FloatTensor(2,3)
out:tensor([[-4.7295e+03, 4.5726e-41, -4.7295e+03],
[ 4.5726e-41, 4.1312e-05, 1.4073e+19]])
in:a.shape[1]#要和size方法区分开
out:3
in:a.size(1)#结果是一样的,输入格式不同
out:3
#shape和size的不同 shape是属性,size是内置方法
in: a.shape
out:torch.Size([2, 3])
in:a.size()
out:torch.Size([2, 3])
dim=3
可以用于 RNN input batch 文字处理
in: b = torch.rand(1,2,3)#随机生成
in:b
out:tensor([[[0.6951, 0.8383, 0.7816],
[0.8623, 0.4354, 0.2093]]])
in:b.shape
out:torch.Size([1, 2, 3])
in:b[0] #返回第一个维度的第0个元素
out:tensor([[0.6951, 0.8383, 0.7816],
[0.8623, 0.4354, 0.2093]])
in:list(b.shape)#直接可以把shape类型转化为list类型
out:[1,2,3]
dim = 4
用于CNN [b,c,h,w]处理图片 b:batch c:channel h:height w:weigh
>>> c = torch.rand(2,2,3,3)
>>> c
tensor([[[[0.9752, 0.0019, 0.0788],
[0.1772, 0.4936, 0.2588],
[0.1061, 0.1911, 0.4890]],
[[0.6045, 0.0807, 0.6464],
[0.7833, 0.2233, 0.4505],
[0.5051, 0.4134, 0.0460]]],
[[[0.7354, 0.2664, 0.1774],
[0.7644, 0.9831, 0.1664],
[0.5349, 0.3107, 0.9049]],
[[0.8138, 0.7909, 0.5750],
[0.9740, 0.7114, 0.6084],
[0.2874, 0.0907, 0.5350]]]])
Mixed
>>> c.numel()#numel 是指tensor占用的内存的数量
36
>>> c.dim()#返回dim大小 dim方法更直观
4
>>>len(c.shape)#返回dim大小
4
四、tensor创建
1、from import numpy
>>> a = np.array([2,3.3])
>>> a
array([2. , 3.3])
>>> torch.from_numpy(a)
tensor([2.0000, 3.3000], dtype=torch.float64)
##数据类型发生改变为torch
>>> data = np.ones([2,3])
>>> type(data)
<class 'numpy.ndarray'>
>>> torch.from_numpy(data)
tensor([[1., 1., 1.],
[1., 1., 1.]], dtype=torch.float64)
2、from import List
>>>torch.tensor([2,3,3])#接收的是数据
tensor([2.0000,3.3000])
>>>torch.Tensor()#接收的是shape 区别与tensor 默认类型为float
>>> torch.set_default_tensor_type(torch.DoubleTensor)#修改默认的类型
>>> torch.tensor([1.2,3]).type()
'torch.DoubleTensor' #默认类型为double
>>>torch.FloatTensor()#接收的是shape 区别于tensor
3、uninitialized
未初始化的tendor一定要跟写入数据的后续步骤,否则可能出现错误
例如 torch.nan 或 torch.infinite 等错误
4、rand/rand_like,randint,randn
rand 会随机产生0~1之间的数值,不包括1
>>> data = torch.rand(3,3)
>>> data
tensor([[0.6656, 0.5422, 0.6965],
[0.8993, 0.1829, 0.7037],
[0.0094, 0.4426, 0.7736]])
#均匀采样0~10的tensor用如下方式
>>> data = 10*torch.rand(3,3)
>>> data
tensor([[8.0830, 4.6255, 9.0585],
[9.6908, 7.3549, 2.7631],
[4.3715, 0.4799, 0.6520]])
rand_like 会生成一个和传入的tensor的shape一样的随机tensor
>>> torch.rand_like(data)
tensor([[0.6300, 0.3401, 0.3261],
[0.8253, 0.5994, 0.4969],
[0.4212, 0.0686, 0.9734]])
randint 参数(min,max,[shape])
其中取值范围[min,max) 前毕后开
>>> data = torch.randint(1,5,[3,3])
>>> data
tensor([[4, 1, 4],
[4, 2, 4],
[3, 2, 1]])
randn 正太分布 N(0,1) 如何自定义mean 和std 这个问题还没解决
>>> data = torch.randn(3,3)
>>> data
tensor([[-0.8080, -0.5170, 0.7041],
[ 0.2044, -0.5794, -0.0975],
[ 0.0389, -1.4845, 1.7123]])
#自定一mean 和std
>>> torch.normal(mean=torch.full([10],0),std=torch.arange(1,0,-0.1))
tensor([-0.4855, -0.1608, 0.1095, 0.4609, 0.3829, 0.5428, -0.0233, 0.4518,
0.0232, 0.1374])
5、full 将数据全部赋值为一个数值 第一个参数是shape
>>> torch.full([2,3],7)
tensor([[7., 7., 7.],
[7., 7., 7.]])
>>> torch.full(data.shape,7)
tensor([[7., 7., 7.],
[7., 7., 7.],
[7., 7., 7.]])
6、arange/range 参数范围也是前闭后开 第三个参数是 步长 torch中不建议用range
>>> torch.arange(0,5,0.5)
tensor([0.0000, 0.5000, 1.0000, 1.5000, 2.0000, 2.5000, 3.0000, 3.5000, 4.0000,
4.5000])
7、linspace/logspace
#linspace 取值范围是前后都是闭集[min,max] 第三个参数是数值的个数
>>> torch.linspace(0,10,4)
tensor([ 0.0000, 3.3333, 6.6667, 10.0000])
#logspace 表示为base^min ~ base^max 之间均匀的steps个数
>>> torch.logspace(0,-1,base = 2,steps=2)
tensor([1.0000, 0.5000])
8、ones/zeros/eye 只用给出shape生成对应的矩阵
ones_like()参数是一个tensor 根据tensor的shape生成一个全1的tensor
eye:单位矩阵
#特别的如果eye给的不是一个方阵会生成如下形式
>>> torch.eye(3,4)
tensor([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.]])
9、randperm() 返回一个随机打散的种子
比如两组数据
data1 (2,3) 的tensor
张三 80 90 90
李四 75 99 98
data2(2,1)
张三 100
李四 99
如果将数据随机打散需要两组数据每个人对应的成绩始终是自己的成绩需要一个种子randperm即返回的是一个种子
#1表示张三,2代表李四
>>> data1 = torch.tensor([[1,80,90,90],[2,75,99,98]])
>>> data1
tensor([[ 1, 80, 90, 90],
[ 2, 75, 99, 98]])
>>> data2 = torch.tensor([[1,100],[2,99]])
>>> data2
tensor([[ 1, 100],
[ 2, 99]])
>>> idx = torch.randperm(2)
#打散后张三始终对应的是自己的成绩,李四也是这样
>>> data1[idx]
tensor([[ 2, 75, 99, 98],
[ 1, 80, 90, 90]])
>>> data2[idx]
tensor([[ 2, 99],
[ 1, 100]])
五、tensor切片
1、dim 0 first
#数据类型
>>> data=torch.rand(4,3,28,28)
>>>> data.shape
torch.Size([4, 3, 28, 28])
>>> data[0,0].shape
torch.Size([28, 28])
>>> data[0,0,2,4]
tensor(0.1039)
2、select first/last N
#[0,1]=2,[0]=1,[0~28)=28,[0~28)=28
>>> data[:2,:1,:,:].shape
torch.Size([2, 1, 28, 28])
#[0,1]=2,[1,2]=2,[0~28)=28,[0~28)=28
>>> data[:2,1:,:,:].shape
torch.Size([2, 2, 28, 28])
#[0,1]=2,[-1]=1,[0~28)=28,[0~28))28
>>> data[:2,-1:,:,:].shape
torch.Size([2, 1, 28, 28])
3、select by steps
#设置步长为2 步长默认为0
>>> data[:,:,0:28:2,0:28:2].shape
torch.Size([4, 3, 14, 14])
4、select by specific index
#注意:第二个参数要声明是tensor即用torch.tensor([]) 说明要取的下标
#dim=0 b=[0,2] 所以取dim=0的0,2两个图
>>>data.index_select(0,torch.tensor([0,2])).shape
torch.Size([2, 3, 28, 28])
#dim=1 c=[1,2] 所以取dim=1的1,2两个通道
>>> data.index_select(1,torch.tensor([1,2])).shape
torch.Size([4, 2, 28, 28])
#dim=2 取[0,1,2,3,4,5,6,7]=8
>>> data.index_select(2,torch.arange(8)).shape
torch.Size([4, 3, 8, 28])
5、 …
主要作用是代替 “::,::,”
更多用来装逼
>>> data[0,...].shape
torch.Size([3, 28, 28])
>>> data[1,...,::2].shape
torch.Size([3, 28, 14])
6、select by mask
masked_select()
>>> data = torch.randn(3,4)
>>> data
tensor([[ 0.3182, 0.6776, 1.8765, 0.2469],
[-0.1910, -0.3214, 0.5434, -0.9586],
[-1.8620, -0.6305, 0.5447, 0.5097]])
>>> mask = data.ge(0.5) #选择大于0.5的下表 mask为'torch.BoolTensor'类型
>>> mask
tensor([[False, True, True, False],
[False, False, True, False],
[False, False, True, True]])
>>> torch.masked_select(data,mask)#得到的是一个vector
tensor([0.6776, 1.8765, 0.5434, 0.5447, 0.5097])
>>> torch.masked_select(data,mask).shape #注意shape改变了
torch.Size([5])
7、select by flatten index
>>> src = torch.tensor([[1,2,3],[8,7,6]])
>>> src
tensor([[1, 2, 3],
[8, 7, 6]])
>>> torch.take(src,torch.tensor([0,2,5]))#先将tensor打平然后在切片
tensor([1, 3, 6])
六、维度变换
1、View/reshape
#变换前后数据量不变理论上可以随意变换 但是有物理意义的变换才有意义
#造成 Loss dim information
>>> data.view(4,3*28*28).shape
torch.Size([4, 2352])
>>> data.reshape(4,3*28*28).shape
torch.Size([4, 2352])
>>> 784*3
2352
2、Squeeze/unsqueeze
#理解方式发生改变
#一个List的范围 [-a.index()-1,a.index()+1)
#比如[0,1,2] 可取范围[-3~0 ~3)可取
#最好不用负数,容易混淆
>>> b
tensor([0, 1, 2])
>>> b[-3]
tensor(0)
>>> b[-2]
tensor(1)
>>> b[-1]
tensor(2)
>>> b = torch.randn(1,32,1,1)
>>> b.shape
torch.Size([1, 32, 1, 1])
>>> b.squeeze().shape
torch.Size([32])
>>> b.squeeze(0).shape#将dim=0挤压掉
torch.Size([32, 1, 1])
**#注意:当挤压的shape 对应size不是1时不会报错,也不会改变**
>>> b.squeeze(1).shape
torch.Size([1, 32, 1, 1])
>>> data.shape
torch.Size([4, 3, 28, 28])
>>> data.unsqueeze(0).shape#在前面增加dim 可以理解为增加一个组的概念
torch.Size([1, 4, 3, 28, 28])
>>> data.unsqueeze(-1).shape#在后面增加dim
torch.Size([4, 3, 28, 28, 1])
3、Transpose/t/permute
#矩阵转置 t()只能用在矩阵中
>>> c = torch.randn(3,4)
>>> c
tensor([[-0.4113, 0.9222, 0.5007, 1.2305],
[-0.4973, -0.0965, 0.3321, -0.6471],
[-1.1971, 0.6471, 0.1007, -0.4319]])
>>> c.t()
tensor([[-0.4113, -0.4973, -1.1971],
[ 0.9222, -0.0965, 0.6471],
[ 0.5007, 0.3321, 0.1007],
[ 1.2305, -0.6471, -0.4319]])
>>> c.t().shape
torch.Size([4, 3])
#transpose
#数据的维度顺序必须与存储顺序一致
#view会导致维度顺序关系变模糊,所以需要人为跟踪
#contiguous函数将数据连续
>>> data.shape
torch.Size([4, 3, 28, 28])
>>>a1 = data.transpose(1,3).contiguous().view(4,3*28*28).view(4,3,28,28)#
>>>a2 = data.transpose(1,3).contiguous().view(4,3*28*28).view(4,28,28,3).transpose(1,3)
>>>a1.shape
torch.Size([4, 3, 28, 28])
>>> a2.shape
torch.Size([4, 3, 28, 28])
>>> torch.all(torch.eq(data,a1))#虽然shape一样但是改变了存储顺序
tensor(False)
>>> torch.all(torch.eq(data,a2))#a2的方式才是正确的方式
tensor(True)
#下边这种情况就会报错,修改了存储的维度顺序
>>> a = data.transpose(1,3).view(4,3*28*28).view(4,3,28,28)
# permute
#推荐使用
>>> data = torch.randn(4,3,28,32)
>>> data.shape
torch.Size([4, 3, 28, 32])
#permute传入一个新的顺序就能完成复杂的变换
>>> data.permute(0,2,3,1).shape
torch.Size([4, 28, 32, 3])
4、Expand/repeat
#expand:broadcasting 先扩展后需要时复制数据 推荐使用
#repeat :memory copied 主动复制内存数据
#expand
>>> b.shape
torch.Size([1, 32, 1, 1])
>>> data.shape
torch.Size([4, 3, 28, 28])
#只有原来相应维度是1 才能扩展为其他 -1代表相应维度不扩展
>>> b.expand(4,-1,28,28).shape
torch.Size([4, 32, 28, 28])
#如果是 data.expand(-1,32,-1,-1)#会报错The expanded size of the tensor (32) must match the existing size (3) at non-singleton dimension 1
#repeat
>>> b.shape
torch.Size([1, 32, 1, 1])
#参数代表相应位置要重复的次数
>>> b.repeat(4,32,1,1).shape
torch.Size([4, 1024, 1, 1]) #(4*1,32*32,1*1,1*1)
进阶七、BroadCast
功能:1、Expand
2、without copying data
broadcast步骤:1、Insert 1 dim ahead
2、Expand dims with size 1 to same size
如果维度不相同会需要扩展的维度会先从小维度与要扩展到的目标维度对齐,然后在insert
小维度:[2,3,32,28] # 28就是最小的维度,往左依次增大
例如:bias向feature扩展
BroatCast过程
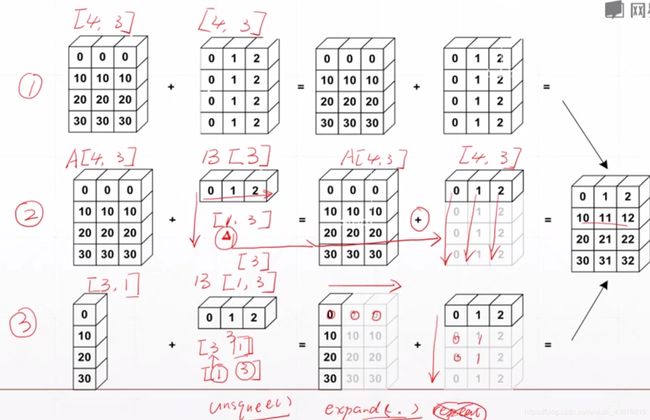
#一个实际的例子:
#data代表4个班级每个班级32个人,每人有8门课程成绩
>>> data = torch.randn(4,32,8)
#shape【4,32,8】
>>> data.shape
torch.Size([4, 32, 8])
#要为每个学生每门课加0.5分
>>> score = torch.tensor([0.5])
#每个学生只对第三门课加0.5分
#>>> score = torch.tensor([0,0,0.5,0,0,0,0,0])
>#shape【1】
>>> score.shape
torch.Size([1])
1.#手动扩展扩展score 为【4,32,8】
>>> score = score.unsqueeze(0).unsqueeze(0).expand_as(data)
>>> score.shape
torch.Size([4, 32, 8])
2.#用BroadCast方法
3.用full方法
>>> value = torch.full([4,32,8],0.5)
>>> value.shape
torch.Size([4, 32, 8])
以上三种方法都可完成任务,但是手动扩展比较麻烦而且这里用的是expand方法如果用repeat方法会占用大量内存(例如[0.5]一个浮点数4byte,用expand方法只是扩展没有复制数据直到需要用到数据时才会复制 ,而repeat方法会直接复制数据造成4328*4byte内存占用)BroadCast采用的是expand方式扩展。第三种方法也是会占用大量内存。
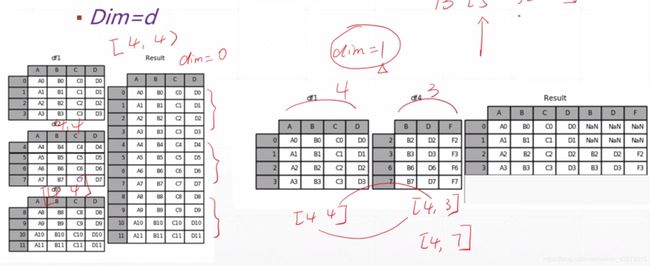
八、拆分与拼接
1、Cat
#cat时要求非cat维度必须保持一直 cat的维度可以不一直
#dataA代表4个班级的成绩,dataB代表5个班级的成绩
#将这9个班级的成绩合并到一起成为一个大表,这里不同于stack后边说明
>>> dataA = torch.rand(4,32,8)
>>> dataB = torch.rand(5,32,8)
>>> dataA.shape
torch.Size([4, 32, 8])
>>> dataB.shape
torch.Size([5, 32, 8])
>>> torch.cat([dataA,dataB],dim=0).shape
torch.Size([9, 32, 8])
#说明一下上图右边那种情况,是经过特殊方法实现行号对其
#正常情况是如下列子
>>> a = torch.zeros(4,4)
>>> b = torch.ones(4,3)
>>> torch.cat([a,b],dim=1).shape
torch.Size([4, 7])
>>> torch.cat([a,b],dim=1)
tensor([[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]])
2、Stack
区别与cat的方面:1.creat new dim
2.两个tensor所有维度的size必须相同
#两个班级的成绩表dataA ,dataB
#要将两个成绩表合并做如下操作
>>> dataA = torch.rand(32,8)
>>> dataB = torch.rand(32,8)
>>> dataA.shape
torch.Size([32, 8])
>>> dataB.shape
torch.Size([32, 8])
>>> torch.stack([dataA,dataB],dim=0).shape
torch.Size([2, 32, 8])
#如果两tensor的一个维度不相同进行stack会出错
>>> dataB = torch.rand(32,4)
>>> torch.stack([dataA,dataB],dim=0).shape
#invalid argument 0: Sizes of tensors must match except in dimension 0. Got 8 and 4 in dimension 2 at /pytorch/aten/src/TH/generic/THTensor.cpp:689
3、Split 根据len拆分
注意:split返回的类型是tuple 是将拆分后的tensor放到一个tuple中
#第一种 拆分的长度相同
>>> dataA.shape
torch.Size([4, 32, 8])
#这一点需要注意,如果是用多个变量接收拆分的tensor结果是每个变量指向一个tensor
>>> aa,bb = dataA.split(2,dim=0)
>>> aa.shape
torch.Size([2, 32, 8])
>>> type(aa)
<class 'torch.Tensor'>
>>> bb.shape
torch.Size([2, 32, 8])
#实际上split返回的是一个tuple类型
>>> cc = dataA.split(2,dim=0)
>>> type(cc)
<class 'tuple'>
>>> type(cc[0])
<class 'torch.Tensor'>
#第二种 拆分的长度不同
>>> dataB.shape
torch.Size([5, 32, 8])
>>> dd,ee = dataB.split([2,3],dim=0)
>>> dd.shape
torch.Size([2, 32, 8])
>>> ee.shape
torch.Size([3, 32, 8])
4、Chunk 根据num拆分
#这里是根据拆分后的数量 比如四个拆成两个就是长度4/2 五个拆成两个默认拆成长度为3和2的两个
>>> dataA.shape
torch.Size([4, 32, 8])
>>> aa,bb = dataA.chunk(2,dim=0)
>>> aa.shape
torch.Size([2, 32, 8])
>>> bb.shape
torch.Size([2, 32, 8])
>>> cc = dataB.chunk(2,dim=0)
>>> cc[0].shape
torch.Size([3, 32, 8])
>>> cc[1].shape
torch.Size([2, 32, 8])
九、基本数学运算
数学符号:+ - × /
函数形式:add sub mul div
乘法是基于element-wise计算的,矩阵乘法会在下边说明
用数学符号和函数方法结果是一样的
>>> a = torch.zeros(3,4)
>>> a
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
>>> b = torch.ones(4)
>>> b
tensor([1., 1., 1., 1.])
#用到了BroadCast机制
>>> a+b
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
#用数学符号和函数的方法结果相同
>>> dataA = torch.rand(3,4)
>>> dataB = torch.rand(4)
#两种方式结果相等
>>> torch.all(torch.eq(dataA*dataB,torch.mul(dataA,dataB)))
tensor(True)
matmul矩阵乘法
>>> dataA = torch.full([2,2],3)
>>> dataA
tensor([[3., 3.],
[3., 3.]])
>>> dataB = torch.ones(2,2)
#特别说明这里的mm方法只适用于2D
>>> torch.mm(dataA,dataB)
tensor([[6., 6.],
[6., 6.]])
>>> torch.matmul(dataA,dataB)
tensor([[6., 6.],
[6., 6.]])
>>> dataA@dataB
tensor([[6., 6.],
[6., 6.]])
#高纬的矩阵相乘
>>> dataA = torch.rand(4,3,28,64)
>>> dataB = torch.rand(4,3,64,32)
>>> dataA.shape,dataB.shape
(torch.Size([4, 3, 28, 64]), torch.Size([4, 3, 64, 32]))
#将后边两个维度矩阵相乘
>>> torch.matmul(dataA,dataB).shape
torch.Size([4, 3, 28, 32]
#用了BroadCast机制
>>> temp = torch.rand(3,64,32)
>>> torch.matmul(dataA,temp).shape
torch.Size([4, 3, 28, 32])
举个例子:
#将(4,784)降到(4,512)
>>> x = torch.rand(4,784)
#pytorch默认w的写法 第一个参数是out 第二个是in
>>> w = torch.rand(512,784)
#所以这里需要转置t函数(如果是高维需要用transpose)
>>> (x@w.t()).shape
torch.Size([4, 512])
#实际上[email protected]()+b
power
平方:pow **2
开方:sqrt **0.5
>>> a = torch.full([2,2],3)
>>> a**2
tensor([[9., 9.],
[9., 9.]])
#pow函数有两种方法
>>> a.pow(2)
tensor([[9., 9.],
[9., 9.]])
>>> pow(a,2)
tensor([[9., 9.],
[9., 9.]])
>>> aa = a**2
#square root
>>> aa.sqrt()
tensor([[3., 3.],
[3., 3.]])
#先开平方根然后倒数
>>> aa.rsqrt()
tensor([[0.3333, 0.3333],
[0.3333, 0.3333]])
#也是平方根
>>> aa**(0.5)
tensor([[3., 3.],
[3., 3.]])
Exp log
log :log(以e为底) log2(以2为底) log10(以10为底)
exp:基数为e ≈ 2.7183
>>> a = torch.exp(torch.ones(2,2))
>>> a
tensor([[2.7183, 2.7183],
[2.7183, 2.7183]])
>>> torch.log(a)
tensor([[1., 1.],
[1., 1.]])
Approximation
.floor() :向下取整
.ceil() :向上取整
.round() :四舍五入
.trunc() :只取整数部分
.frac() : 只取小数部分
>>> data = torch.tensor(3.14)
>>> data
tensor(3.1400)
>>> data.floor(),data.ceil(),data.trunc(),data.frac()
(tensor(3.), tensor(4.), tensor(3.), tensor(0.1400))
Clamp
clamp(min,max)
>>> grad = torch.rand(2,3)*15
>>> grad
tensor([[13.3316, 11.0164, 2.2534],
[11.8352, 13.8210, 1.2795]])
#将数限制在(0~10)之间,大于10的赋值为10 小于0的赋值为零
>>> grad.clamp(0,10)
tensor([[10.0000, 10.0000, 2.2534],
[10.0000, 10.0000, 1.2795]])
>>> grad[0][2] = -0.11
>>> grad
tensor([[13.3316, 11.0164, -0.1100],
[11.8352, 13.8210, 1.2795]])
>>> grad.clamp(0,10)
tensor([[10.0000, 10.0000, 0.0000],
[10.0000, 10.0000, 1.2795]])
十、属性统计
1、norm :仅指范数 区别与normalize
norm(p,dim)
>>> a = torch.full([8],1)
>>> b = a.view(2,4)
>>> c = a.view(2,2,2)
>>> b
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]])
>>> c
tensor([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]])
#1范式
>>> a.norm(1),b.norm(1),c.norm(1)
(tensor(8.), tensor(8.), tensor(8.))
>>> a.norm(2),b.norm(2),c.norm(2)
(tensor(2.8284), tensor(2.8284), tensor(2.8284))
#加入维度求范数
>>> b.norm(1,dim=1)
tensor([4., 4.])
>>> b.norm(2,dim=1)
tensor([2., 2.])
>>> c.norm(1,dim=0)
tensor([[2., 2.],
[2., 2.]])
>>> c.norm(2,dim=1)
tensor([[1.4142, 1.4142],
[1.4142, 1.4142]])
2、mean sum
3、prod
4、max,min,argmin,argmax
5、keepdim
#默认情况会将多维打平为一维后在进行统计计算,如果需要仅在一个维度进行操作要给dim参数
>>> data = torch.arange(8).view(2,4).float()
>>> data
tensor([[0., 1., 2., 3.],
[4., 5., 6., 7.]], dtype=torch.float32)
#prod 累乘
>>> data.min(),data.max(),data.mean(),data.prod()
(tensor(0., dtype=torch.float32), tensor(7., dtype=torch.float32), tensor(3.5000, dtype=torch.float32), tensor(0., dtype=torch.float32))
>>> data.sum()
tensor(28., dtype=torch.float32)
#返回最大值和最小值的索引
#默认情况会将多维打平后再做统计计算
>>> data.argmax(),data.argmin()
(tensor(7), tensor(0))
#添加维度
>>> data = torch.rand(4,10)
>>> data[0]
tensor([0.5849, 0.9449, 0.0877, 0.1710, 0.9037, 0.4782, 0.4373, 0.7225, 0.2574,
0.5914])
#要统计的dim会消去 比如dim=1,则对应的data.shape中dim=1的维度就消去了
>>> data.argmax(dim=1)
tensor([1, 5, 8, 4])
>>> data.argmax(dim=0)
tensor([2, 0, 3, 1, 3, 1, 1, 2, 2, 0])
#keepdimm 设置keepdim=True 则结果仍然和数据原维度一样
>>> data.argmax(dim=0,keepdim=True)
tensor([[2, 0, 3, 1, 3, 1, 1, 2, 2, 0]])
6、kthvalue,topk
kthvalue与topk的区别:1.kthvalue只能取第k小,topk可以取k个大和k个小 (根据largest设置的值)
2.kthvalue只返回第k个,topk返回k个
#最大的前k个
>>> data.topk(3,dim=1)
torch.return_types.topk(
values=tensor([[0.9449, 0.9037, 0.7225],
[0.9424, 0.8019, 0.7210],
[0.9558, 0.8424, 0.7916],
[0.9601, 0.8015, 0.7144]]),
indices=tensor([[1, 4, 7],
[5, 3, 1],
[8, 7, 2],
[4, 2, 0]]))
#largest设置为False 表式返回最小的k个
>>> data.topk(2,dim=1,largest=False)
torch.return_types.topk(
values=tensor([[0.0877, 0.1710],
[0.1684, 0.3603],
[0.1289, 0.2839],
[0.1078, 0.1396]]),
indices=tensor([[2, 3],
[9, 8],
[9, 4],
[1, 6]]))
#kthvalue
#返回第k小的值和索引
>>> data.kthvalue(8,dim=1)
torch.return_types.kthvalue(
values=tensor([0.7225, 0.7210, 0.7916, 0.7144]),
indices=tensor([7, 1, 2, 0]))
7、compare
#> < >= <= != ==
#eq 和 equal 返回的结果的类型不同
>>> temp = torch.ones(2,3)
>>> temp1 = torch.ones(2,3)
>>> torch.eq(temp,temp1)
tensor([[True, True, True],
[True, True, True]])
>>> torch.equal(temp,temp1)
True
十一、where&gather
where
torch.wheee(condition,x,y)->Tensor
Reeturn a tensor of elements selected from either x or y, depending on condition.
The operation is defined as:
>>> cond = torch.tensor([[0.6769,0.7271],[0.8884,0.4163]])
>>> cond
tensor([[0.6769, 0.7271],
[0.8884, 0.4163]])
>>> cond>0.5
tensor([[ True, True],
[ True, False]])
>>> a = torch.zeros(2,2)
>>> a
tensor([[0., 0.],
[0., 0.]])
>>> b = torch.ones(2,2)
>>> b
tensor([[1., 1.],
[1., 1.]])
>>> torch.where(cond>0.5,a,b)
tensor([[0., 0.],
[0., 1.]])
gather
torch.gather(input,dim,index,out=None) ->Tensor
Gathers values along an axis specified by dim.
For a 3-D tensor the output is specified by:
out[i][j][k] = input[index[i][j][k][j][k] #if dim=0
out[i][j][k] = input[i][index[i][j][k][k]#if dim=0
out[i][j][k] = input [i][j] [index[i][j][k]]#if dim=0
>>> prob = torch.randn(4,10)
>>> idx = prob.topk(3,dim=1)
>>> idx[1]
tensor([[2, 3, 7],
[2, 1, 0],
[2, 5, 7],
[3, 1, 4]])
>>> label = torch.arange(10)+100
>>>torch.gather(label.expand(4,10),dim=1,index = idx[1].long())
tensor([[102, 103, 107],
[102, 101, 100],
[102, 105, 107],
[103, 101, 104]])
>>> idx[1]
tensor([[2, 3, 7],
[2, 1, 0],
[2, 5, 7],
[3, 1, 4]])
十二、梯度和激活函数
1、initialization
2、learning rate
3、movement :escape minima
激活函数
模型:
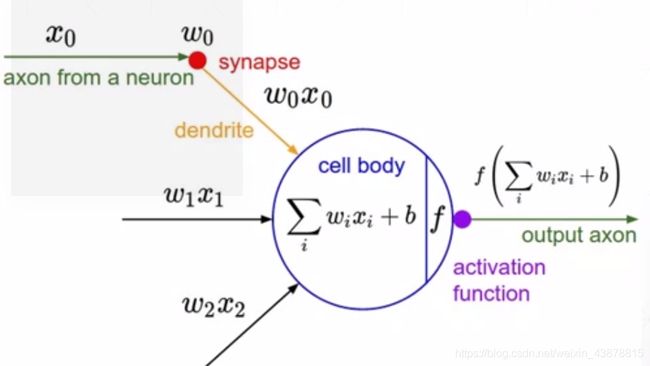 数学模型
数学模型 函数图
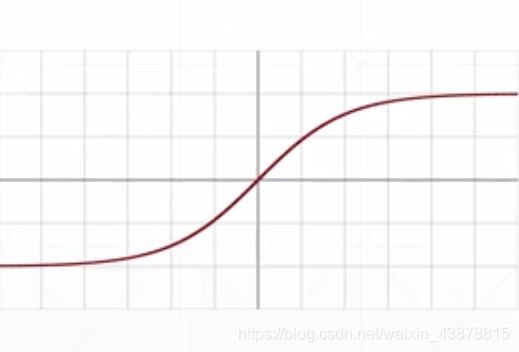
函数图 sigmoid/logistic
sigmoid/logistic
f ( x ) = δ ( x ) = 1 1 + e − x f( x )= \delta ( x )={{1} \over { {1}+ e^{-x} }} f(x)=δ(x)=1+e−x1
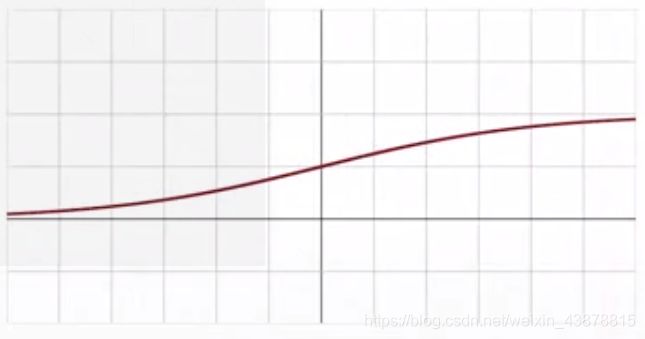
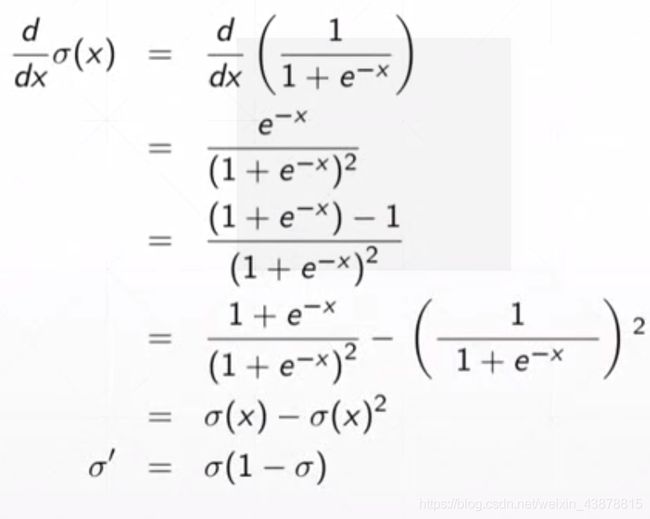
>>> data = torch.linspace(-100,100,10)
>>> data
tensor([-100.0000, -77.7778, -55.5556, -33.3333, -11.1111, 11.1111,
33.3333, 55.5556, 77.7778, 100.0000])
>>> torch.sigmoid(data)
tensor([3.7201e-44, 1.6655e-34, 7.4564e-25, 3.3382e-15, 1.4945e-05, 9.9999e-01,
1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00])
梯度弥散:梯度等于零长时间导致参数没有改变的情况。
1.learning rate 过大
2.gradient xxx
3.初始化
>>> data = torch.linspace(-1,1,10)
>>> data
tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000])
>>> torch.tanh(a)
tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107, 0.1107, 0.3215, 0.5047,
0.6514, 0.7616])
>>> from torch.nn import functional as F
>>> a = torch.linspace(-1,1,10)
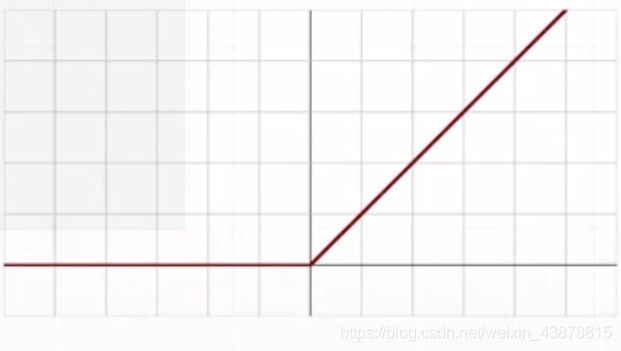
>>> torch.relu(a)
tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])
>>> F.relu(a)
tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])
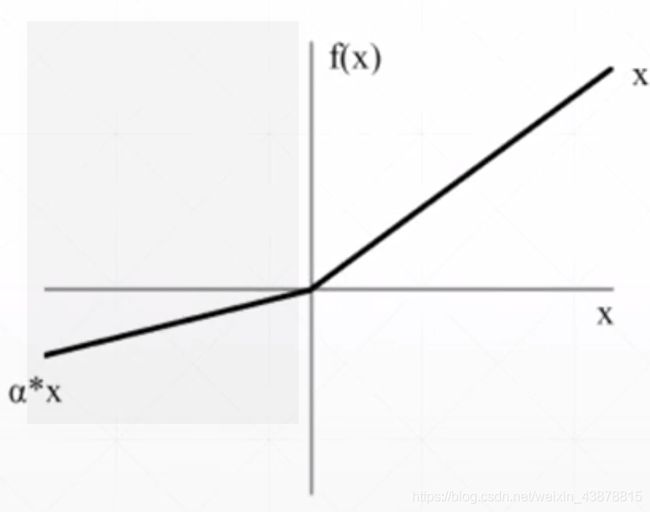
torch.nn.LeakyReLU(negative_slope,inplace)#negative_slope 默认为1e-2,inplace默认为False
SELU
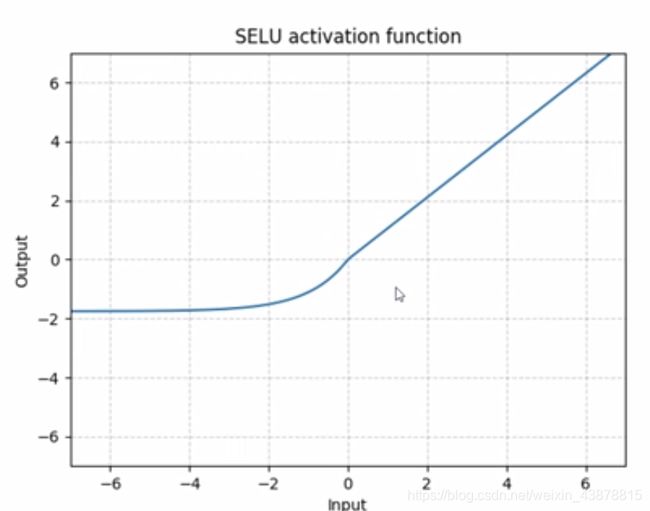
S E L U ( x ) = s c a l e ∗ ( m a x ( 0 , x ) + m i n ( 0 , α ∗ ( e x p ( x ) − 1 ) ) ) w i t h α = 1.6732632423543772848170429916717 a n d s c a l e = 1.0507009873554804934193349852946 SELU( x )= scale*( max(0,x ) +min( 0, \alpha *(exp(x)-1))) with \alpha =1.6 732632423543772848170429916717 and scale = 1.0507009873554804934193349852946 SELU(x)=scale∗(max(0,x)+min(0,α∗(exp(x)−1)))withα=1.6732632423543772848170429916717andscale=1.0507009873554804934193349852946
Softplus
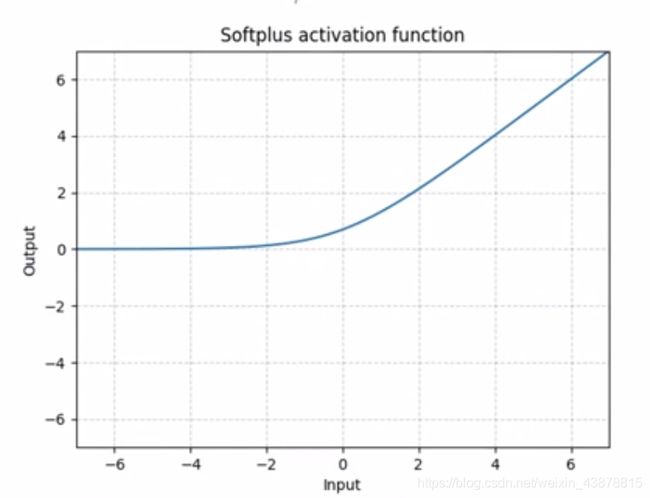
S o f t p l u s ( x ) = 1 o v e r β ∗ l o g ( 1 + e x p ( β ∗ x ) ) Softplus( x ) = {1} over { \beta } * log( 1+exp(\beta * x) ) Softplus(x)=1overβ∗log(1+exp(β∗x))
Mean Squared Error
#pred = xw+b
>>> x = torch.ones(1)
>>> w = torch.full([1],2)
>>> mse = torch.mse_loss(torch.ones(1),x*w)
>>> mse = F.mse_loss(torch.ones(1),x*w)#动态图建图
>>> mse
tensor(1.)
>>> torch.autograd.grad(mse,[w])#由于一开始w没有设置为需要grad信息所以这里报错
#RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
>>> w.requires_grad_()#给w添加grad信息
tensor([2.], requires_grad=True)#显示设置成功
#然而再次自动求导扔会出错,这里就体现出pytorch是动态图的机制,
#做一步计算一步图,w更新了然而图还没有更新所以导致这里使用的还是原始的图结果仍然报错。
>>> torch.autograd.grad(mse,[w])
#RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
>>> mse = F.mse_loss(torch.ones(1),x*w)
>>> torch.autograd.grad(mse,[w])
(tensor([2.]),)#这里最好自己手算一下加深理解
###############################
#第二种方式
>>> mse = F.mse_loss(torch.ones(1),x*w)
#backward向后传播,自动计算这条图路径上所有tensor需要grad的计算。计算结果直接保存到每个tensor的成员变量中。通过x.grad的方法调用
>>> mse.backward()
>>> w.grad
tensor([2.])
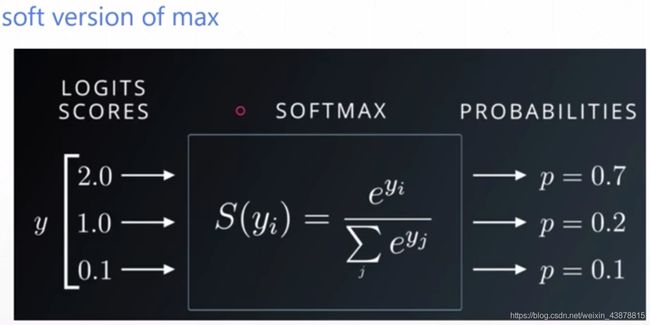
softmax
会将原始数据差距较小的增大它们的区分度,而且最后结果的概率加起来为1(这是区别取sigmoid)

>>> a = torch.rand(3)
>>> a.requires_grad_()
tensor([0.5942, 0.2339, 0.1157], requires_grad=True)
>>> p = F.softmax(a,dim=0)
>>> p[1]
tensor(0.3010, grad_fn=<SelectBackward>)
#这里也应证了上边公式,当i=j时gradient>0 i!=j时gradient<0
>>> torch.autograd.grad(p[1],[a],retain_graph=True)
(tensor([-0.1299, 0.2104, -0.0805]),)
>>> torch.autograd.grad(p[2],[a],retain_graph=True)
(tensor([-0.1154, -0.0805, 0.1959]),)
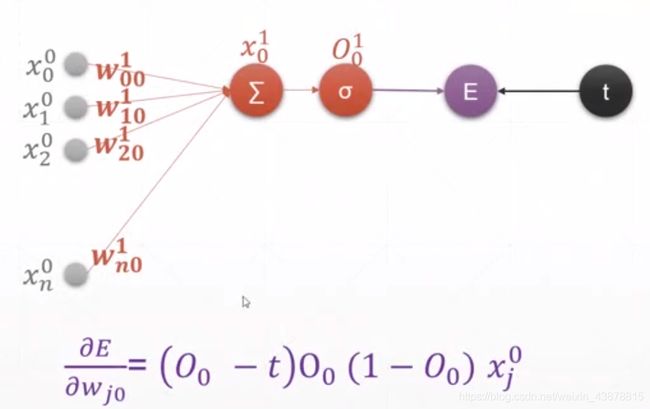
十三、感知机的梯度推导
#单层感知机
>>> x = torch.randn(1,10)
>>> w = torch.randn(1,10,requires_grad=True)#设置w可导
>>> o = torch.sigmoid(x@w.t())#激活函数作用
>>> o.shape
torch.Size([1, 1])
>>> loss = F.mse_loss(torch.ones(1,1),o)#计算loss
>>> loss
tensor(0.4645, grad_fn=<MeanBackward0>)
>>> loss.shape
torch.Size([])
>>> loss.backward #求导
<bound method Tensor.backward of tensor(0.4645, grad_fn=<MeanBackward0>)>
>>> loss.backward()
>>> w.grad #梯度的作用是更新w值 找到一个优化的w值
tensor([[-0.3271, 0.1460, -0.0213, -0.3426, -0.3098, -0.1252, -0.2221, 0.1417,
-0.0587, -0.1922]])
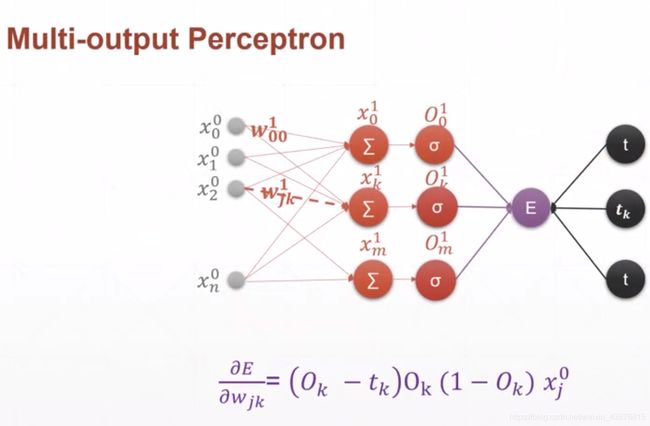
#多输出
>>> x = torch.randn(1,10)
>>> w = torch.randn(2,10,requires_grad=True)
>>> o = torch.sigmoid(x@w.t())
>>> o.shape
torch.Size([1, 2])
>>> loss = F.mse_loss(torch.ones(1,2),o)
>>> loss
tensor(0.3536, grad_fn=<MeanBackward0>)
>>> loss.backward()
>>> w.grad
tensor([[ 0.0138, 0.0062, 0.0026, 0.0023, -0.0091, -0.0411, 0.0024, 0.0065,
-0.0455, 0.0396],
[ 0.0847, 0.0377, 0.0157, 0.0141, -0.0554, -0.2517, 0.0149, 0.0400,
-0.2786, 0.2421]])
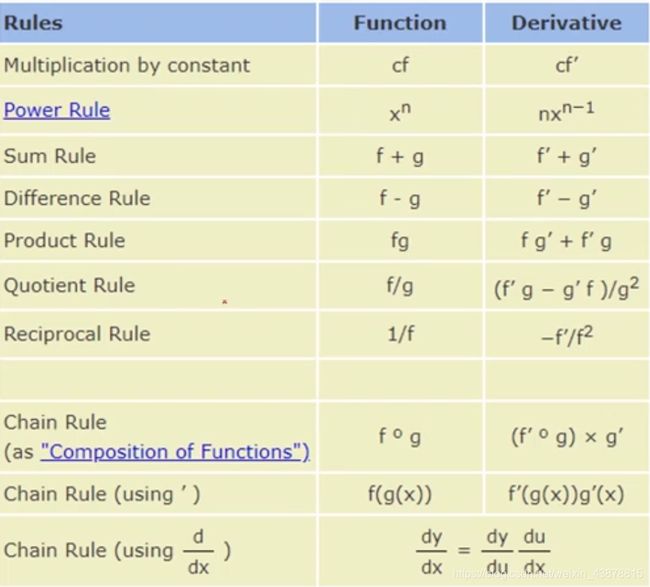
#链式法则
>>> x = torch.tensor(1.)
>>> w1 = torch.tensor(2.,requires_grad=True)
>>> b1 = torch.tensor(1.)
>>> w2 = torch.tensor(2.,requires_grad=True)
>>> b2 = torch.tensor(1.)
>>> y1 = x*w1+b1
>>> y2 = y1*w2+b2
>>> dy2_dy1 = torch.autograd.grad(y2,[y1],retain_graph=True)[0]
>>> dy1_dw1 = torch.autograd.grad(y1,[w1],retain_graph=True)[0]
>>> dy2_dw1 = torch.autograd.grad(y2,[w1],retain_graph=True)[0]
>>> dy2_dy1*dy1_dw1
tensor(2.)
>>> dy2_dw1
tensor(2.)
反向传播
推导过程在本子上。
一个实例 :/root/PycharmProjects/pytorch
十四、交叉熵
Entropy
1.Uncertainty
2.measure of surprise
3.higher entropy = less info.
E n t r o p y = − ∑ P ( i ) l o g P ( i ) Entropy = -∑P(i)logP(i) Entropy=−∑P(i)logP(i)
Cross Entropy
H ( p , q ) = − ∑ p ( x ) l o g q ( x ) ; H ( p , q ) = H ( p ) + D K L ( p ∣ q ) H(p,q) = -∑p(x)log q(x); H(p,q) = H(p)+D_{KL}(p|q) H(p,q)=−∑p(x)logq(x);H(p,q)=H(p)+DKL(p∣q)
当P=Q时
Cross Entropy = Entropy
此时Divergence =0
for one-hot encoding
entroy = 1log1 = 0
根据Cross Entropy 公式得H§=0
所以:
H ( p , q ) = 0 + D K L ( p ∣ q ) H(p,q) = 0 +D_{KL}(p|q) H(p,q)=0+DKL(p∣q)
优化Cross Entropy时就是在优化p和q的K-L Divergence 当K-L Divergence接近于零时证明p与q越接近.
==这个K-L 与工程优化上的K-L是否一致? ==
Binary classification 推导
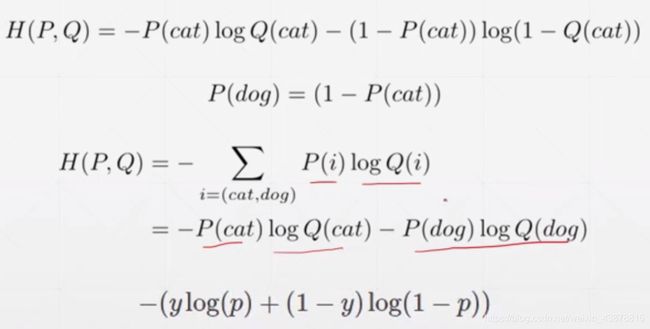
 一个主流神经网络结构
一个主流神经网络结构

注意:
>> w.shape
torch.Size([10, 784])
>>> x.shape
torch.Size([1, 784])
>>> logits = x@w.t()
>>> logits.shape
torch.Size([1, 10])
>>> pred= F.softmax(logits,dim=1)
>>> pred.shape
torch.Size([1, 10])
>>> pred_log = torch.log(pred)
>>> F.cross_entropy(logits,torch.tensor([3]))#这里一定是logits不是pred ,因为在pytorch中已经将softmax和log打包到cross_entropy中
tensor(53.3119)
>>> F.nll_loss(pred_log,torch.tensor([3]))
tensor(53.3119)
#结论是 cross_entropy函数=softmax+log+nll_loss
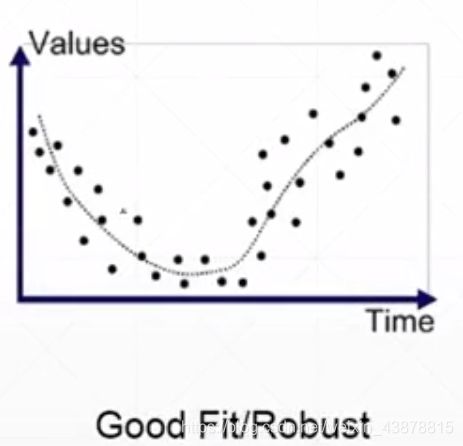
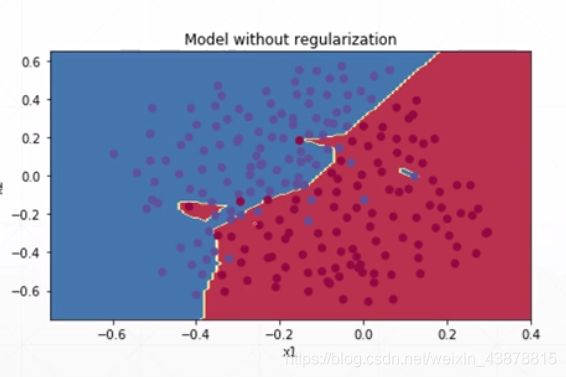
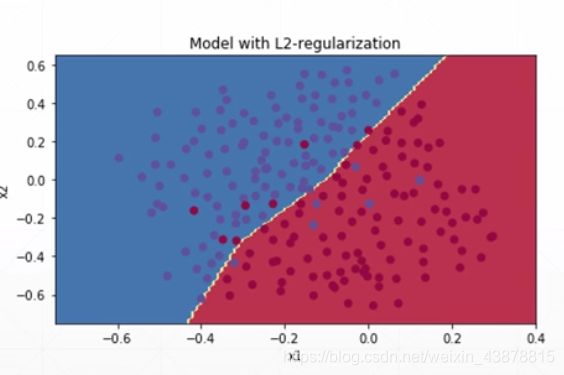
十五、过拟合和欠拟合
underfitted:train acc. is bad
test acc. is bad as well
overfitted:train loss and acc. is much better
test acc. is worse
other way :generalizetion performance is worse

通过Train -Validation -Test划分避免overftteed
Train Set 训练模型,更新参数
Validation Set 挑选参数,保留训练模型表现最好的参数
Test Set 测试模型
如果用Test Set 去挑选参数会导致数据污染,是一种作弊行为。
K-fold cross validation
1.merge train/validation sets
2.randomly sample 1/k as validation set
动量衰减