【数据结构第五章】- 二叉树（万字详解）
目录
一、二叉树
1.1 - 二叉树的定义
1.2 - 二叉树的性质
1.3 - 特殊的二叉树
二、二叉树的顺序存储结构
2.1 - 堆的定义
2.2 - 堆的实现
2.2.1 - Heap.h
2.2.2 - Heap.c
2.2.3 - test.c
2.3 - 堆的应用
2.3.1 - 堆排序
2.3.2 - Top-K 问题
三、二叉树的链式存储结构
3.1 - 遍历二叉树
3.1.1 - 递归算法
3.1.2 - 非递归算法
3.1.3 - 层序遍历
3.2 - 二叉树遍历算法的应用
3.2.1 - #号法创建二叉树
3.2.2 - 复制二叉树
3.2.3 - 计算二叉树的深度
3.2.4 - 统计二叉树中结点个数
3.2.5 - 查找二叉树中的结点
3.2.6 - 销毁二叉树
一、二叉树
1.1 - 二叉树的定义
二叉树（Binary Tree）是 n（n >= 0）个结点所构成的集合，它或为空树（n = 0）；或为非空树，对于非空树 T：
-
有且仅有一个称之为根的结点；
-
除根结点以外的其余结点分为两个互不相交的子集 T1 和 T2，分别称为 T 的左子树和右子树，且 T1 和 T2 本身又都是二叉树。
二叉树与树一样具有递归性质，二叉树与树的区别主要有以下两点：
-
二叉树每个结点至多有两棵子树（即二叉树中不存在度大于 2 的结点）；
-
二叉树的子树有左右之分，其次序不能颠倒。
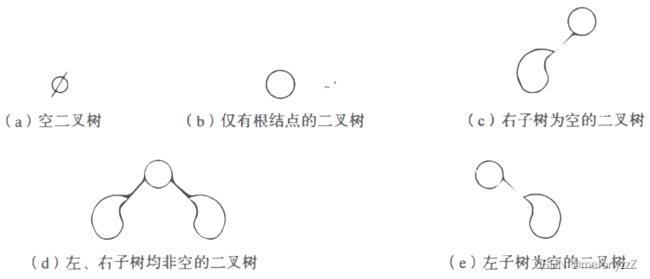
二叉树有以下 5 种基本形态：
1.2 - 二叉树的性质
-
在二叉树的第
i层上至多有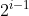 
个结点（i >= 1）。 -
深度为 k 的二叉树至多有
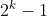个结点（k >= 1）。 -
对任何一棵二叉树 T，如果其终端结点数为
，度为 2 的结点数为 
，则 
。
1.3 - 特殊的二叉树
-
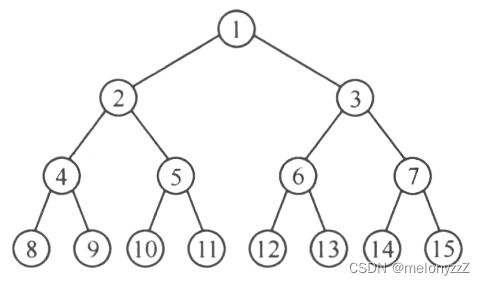
满二叉树：深度为 k 且含有
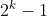个结点的二叉树。下图所示是一棵深度为 4 的满二叉树。
满二叉树的特点是：每一层上的结点数都是最大的结点数，即每一层
i的结点数都具有最大值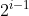。满二叉树的叶子结点都集中在二叉树的最下一层，并且除叶子结点之外的每个结点度数均为 2。可以对满二叉树的结点按层序编号：约定编号从根结点（根结点编号为 1）起，自上而下，自左而右。这样每个结点对应一个编号，对于编号为
i的结点，其左孩子为2i，右孩子为2i + 1，双亲为⌊i / 2⌋（前提是存在的话）。 -
完全二叉树：深度为 k 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时，称之为完全二叉树。下图所示为一棵深度为 4 的完全二叉树。
完全二叉树的特点是：
-
叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点，都依次排列在该层最左边的位置上。
-
若
i <= ⌊n / 2⌋，则结点i为分支结点，否则为叶子结点。 -
若有度为 1 的结点，则只可能有一个，且该结点只有一个左孩子而无右孩子（重要特征）。
-
具有 n 个结点的完全二叉树的深度为 ⌈
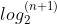⌉ 或者 ⌊
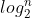⌋ + 1。
-
二、二叉树的顺序存储结构
顺序存储结构使用一组地址连续的存储单元来存储数据元素，为了能够在存储结构中反映结点之间的逻辑关系，必须将二叉树中的结点依照一定的规律安排在这组单元中。
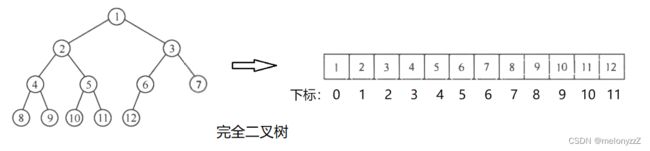
对于完全二叉树，只要从根起按层序存储即可，依次自上而下，自左而右存储结点元素，即将完全二叉树上编号为 i 的结点元素存储在一维数组中下标为 i - 1 的分量中。
下标为
i的结点左孩子为2i + 1，右孩子为2i + 2，双亲为⌊(i - 1) / 2⌋（前提是存在的话）。
对于一般二叉树，则应将其每个结点与完全二叉树上的结点相对照，存储在一维数组的相应分量中。
图中以 "0" 表示不存在此结点。
由此可见，这种顺序存储结构仅适用于完全二叉树。因为，在最坏情况下，一个深度为 k 且只有 k 个结点的单支数（树中不存在度为 2 的结点）却需要长度为 
的一维数组。这造成了存储空间的极大浪费，所以对于一般二叉树，更适合采用链式存储结构。
2.1 - 堆的定义
n 个元素的序列 
称之为堆，当且仅当满足以下条件时：(1) 
且 
（或 (2) 
且 
）。
若将和此序列对应的一维数组（即以一维数组做此序列的存储结构）看成是一个完全二叉树，则堆实质上是满足如下性质的完全二叉树：树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。
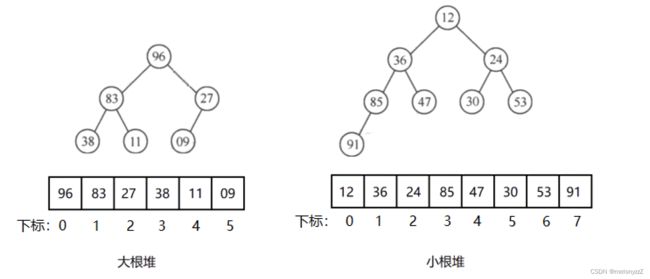
例如，关键字序列 { 96, 83, 27, 38, 11, 09 } 和 { 12, 36, 24, 85, 47, 30, 53, 91 } 分别满足条件 (1) 和条件 (2)，故它们均为堆，对应的完全二叉树如下图所示。
显然，在这两种堆中，堆顶元素（或完全二叉树的根）必为序列中 n 个元素的最大值（或最小值），分别称之为大根堆和小根堆。
2.2 - 堆的实现
2.2.1 - Heap.h
#pragma once
#include
#include
// 堆
#define DEFAULT_CAPACITY 5
typedef int DataType;
typedef struct Heap
{
DataType* data;
int size;
int capacity;
}Heap;
// 基本操作
void HeapInit(Heap* php); // 初始化
bool HeapEmpty(Heap* php); // 判断堆是否为空
void HeapAdjustUp(DataType* data, int child); // 向上调整
void HeapPush(Heap* php, DataType e); // 插入
void HeapAdjustDown(DataType* data, int n, int parent); // 向下调整
void HeapPop(Heap* php); // 删除堆顶元素
DataType HeapTop(Heap* php); // 返回堆顶元素
int HeapSize(Heap* php); // 获取堆中有效元素个数
void HeapDestroy(Heap* php); // 销毁 2.2.2 - Heap.c
-
初始化：
void HeapInit(Heap* php) { assert(php); php->data = (DataType*)malloc(sizeof(DataType) * DEFAULT_CAPACITY); if (NULL == php->data) { perror("initialization failed!"); exit(-1); } php->size = 0; php->capacity = DEFAULT_CAPACITY; } -
判断堆是否为空：
bool HeapEmpty(Heap* php) { assert(php); return php->size == 0; } -
交换两个数据元素：
void Swap(DataType* e1, DataType* e2) { DataType tmp = *e1; *e1 = *e2; *e2 = tmp; } -
插入：
// 向上调整（前提是 data[0] ~ data[child - 1] 均满足大根堆的性质） void HeapAdjustUp(DataType* data, int child) { int parent = (child - 1) / 2; while (child > 0) { if (data[parent] < data[child]) { Swap(&data[parent], &data[child]); child = parent; parent = (child - 1) / 2; } else { break; } } } // 插入 void HeapPush(Heap* php, DataType e) { assert(php); // 判断是否需要扩容 if (php->size == php->capacity) { DataType* tmp = (DataType*)realloc(php->data, sizeof(DataType) * 2 * php->capacity); if (NULL == tmp) { perror("realloc failed!"); return; } php->data = tmp; php->capacity *= 2; } // 将元素插到堆的末尾 php->data[php->size++] = e; // 新插入的元素可能不满足堆（假设为大根堆）的性质，所以需要向上调整 HeapAdjustUp(php->data, php->size - 1); }
如果是小根堆，向上调整的判断条件则应该是
data[parent] > data[child]。 -
删除堆顶元素：
// 向下调整（前提是 data[parent] 左右子树均满足大根堆的性质） void HeapAdjustDown(DataType* data, int n, int parent) { int child = 2 * parent + 1; // 假设左孩子较大 while (child < n) { if (child + 1 < n && data[child + 1] > data[child]) { ++child; } if (data[parent] < data[child]) { Swap(&data[parent], &data[child]); parent = child; child = 2 * parent + 1; } else { break; } } } // 删除堆顶元素 void HeapPop(Heap* php) { assert(php); assert(!HeapEmpty(php)); // 前提是堆非空 // 交换堆顶元素和堆中最后一个元素 Swap(&php->data[0], &php->data[php->size - 1]); // 删除堆顶元素 --php->size; // 此时除了根结点外，其余结点均满足大根堆的性质，所以需要向下调整 HeapAdjustDown(php->data, php->size, 0); }
如果是小根堆，向下调整的判断条件则应该是
data[parent] > data[child]。 -
返回栈顶元素：
DataType HeapTop(Heap* php) { assert(php); assert(!HeapEmpty(php)); // 前提是堆非空 return php->data[0]; } -
获取堆中有效元素个数：
int HeapSize(Heap* php) { assert(php); return php->size; } -
销毁：
void HeapDestroy(Heap* php) { assert(php); free(php->data); php->data = NULL; php->size = 0; php->capacity = DEFAULT_CAPACITY; }
2.2.3 - test.c
void test()
{
Heap hp;
// 初始化
HeapInit(&hp);
// 插入：9 27 11 38 96 83 100
HeapPush(&hp, 9);
HeapPush(&hp, 27);
HeapPush(&hp, 11);
HeapPush(&hp, 38);
HeapPush(&hp, 96);
HeapPush(&hp, 83);
HeapPush(&hp, 100);
printf("当前堆中有效元素个数为：%d\n", HeapSize(&hp)); // 7
// 删除：100 96 83 38 27 11 9
while (!HeapEmpty(&hp))
{
printf("%d ", HeapTop(&hp));
HeapPop(&hp);
}
printf("\n");
// 销毁
HeapDestroy(&hp);
}2.3 - 堆的应用
2.3.1 - 堆排序
堆排序（Heap Sort）是一种树形选择排序。堆排序利用了大根堆（或小根堆）堆顶记录的关键字最大（或最小）这一特征，使得当前无序的序列中选择关键字最大（或最小）的记录变得简单。下面讨论用大根堆进行排序，堆排序的步骤如下：
-
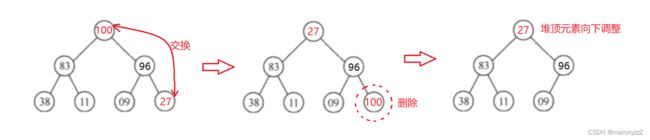
按堆的定义将排序序列 r[0...n-1] 调整为大根堆（这个过程称为建初堆），交换 r[0] 和 r[n - 1]，则 r[n - 1] 为关键字最大的记录。
-
将 r[0...n-2] 重新调整为堆，交换 r[0] 和 r[n - 2]，则 r[n - 2] 为关键字次大的记录。
-
循环 n - 1 次，直到交换了 r[0] 和 r[1] 为止，得到了一个非递减的有序序列 r[0...n-1]。
同样可以通过构造小根堆得到一个非递增的有序序列。
void HeapSort(DataType* data, int n)
{
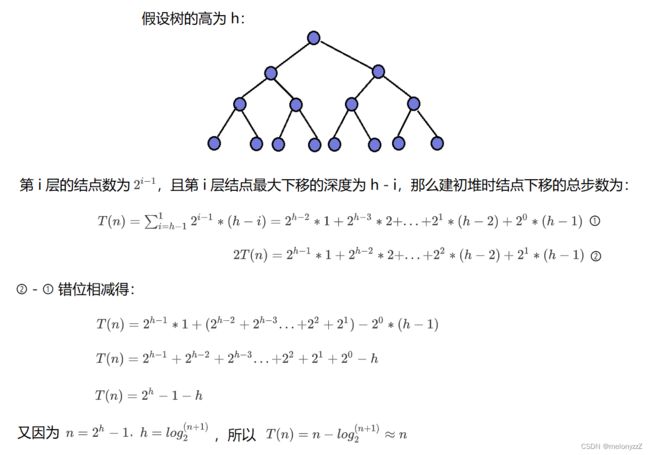
// 建初堆 - 最后一个结点的下标为 n - 1
for (int i = (n - 2) / 2; i >= 0; --i) // (n - 2) / 2 即 [(n - 1) - 1] / 2
{
HeapAdjustDown(data, n, i);
}
// 交换和堆调整
for (int i = n - 1; i > 0; --i)
{
Swap(&data[0], &data[i]);
HeapAdjustDown(data, i, 0);
}
}
建初堆：
要将一个无序序列调整为堆，就必须将其所对应的完全二叉树中以每一个结点为根的子树都调整为堆。显然只有一个结点的树必是堆，而在完全二叉树中，所有下标大于
⌊(n - 2) / 2⌋的结点都是叶子，因此以这些结点为根的子树均已是堆。这样，只需要利用向下调整函数，从最后一个分支结点⌊(n - 2) / 2⌋开始，依次将下标为⌊(n - 2) / 2⌋、⌊(n - 2) / 2⌋ - 1、... ...、0的结点作为根的子树都调整为堆即可。建初堆的时间复杂度：
因为堆是满足一定性质的完全二叉树，为了简化处理，使用满二叉树进行分析。
堆排序的时间复杂度为
O(nlogn)。
2.3.2 - Top-K 问题
问题描述：
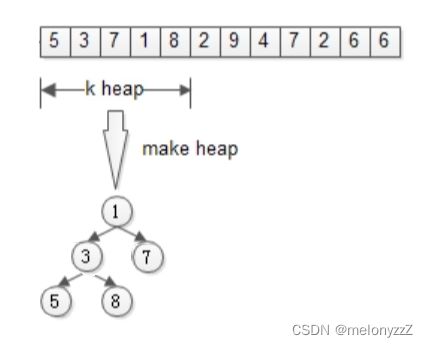
从含有 n 个元素的数组 arr 中，找出最大的 k 个数。
示例：
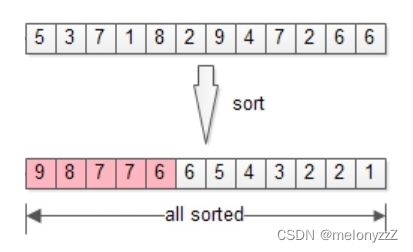
从 arr[12] = { 5, 3, 7, 1, 8, 2, 9, 4, 7, 2, 6, 6 } 这 12 个数中，找出最大的 5 个数。
思路：
-
排序：
最简单直接的办法就是排序，即将 n 个数排好序后，取出前 k 个数。
时间复杂度为
O(nlogn)。 -
局部排序：
由于只需要 Top-K，因此不需要将全局都排序，而只需要排好前 k 个数。
时间复杂度为
O(n*k)。 -
堆：
将全局排序优化为局部排序，是因为非 Top-K 的元素是不需要排序的。实际上最大的 k 个元素也不需要排序，即只要找 Top-K，而不需要排序。
首先用前 k 个元素生成一个小根堆：
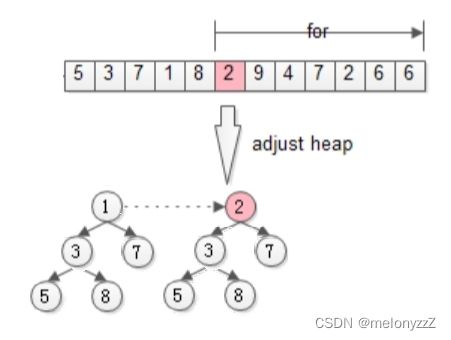
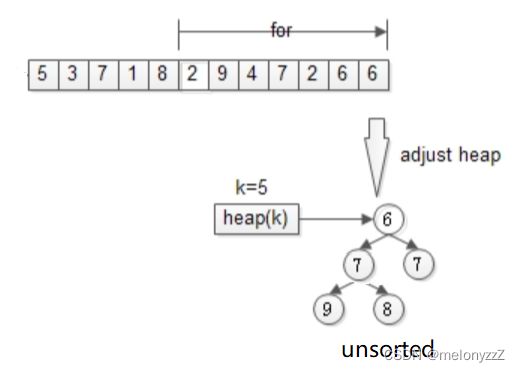
接着，从第 k + 1 个元素开始扫描，和堆顶元素（堆中最小的元素）比较，如果被扫描的元素大于堆顶元素，则替换堆顶元素，并调整堆，以保证堆内的 k 个元素总是当前最大的 k 个元素：
直到扫描完 n - k 个元素，最终堆中的 k 个元素，就是所求的 Top-K：
时间复杂度为
O(nlogk)。如果数据量比较大，不能都加载到内存中，此时最佳的解决方式就是使用堆。
若要找出最小的 k 个数，则应该建大根堆。
int* TopK(int* arr, int n, int k) { // 用 arr 的前 k 个元素建小根堆 int* topk = (int*)malloc(sizeof(int) * k); if (NULL == topk) { perror("malloc failed!"); return NULL; } for (int i = 0; i < k; ++i) { topk[i] = arr[i]; } for (int i = (k - 2) / 2; i >= 0; --i) { HeapAdjustDown(topk, k, i); } // 扫描完剩余的 n - k 个元素 for (int i = k; i < n; ++i) { if (arr[i] > topk[0]) { topk[0] = arr[i]; HeapAdjustDown(topk, k, 0); } } return topk; }
三、二叉树的链式存储结构
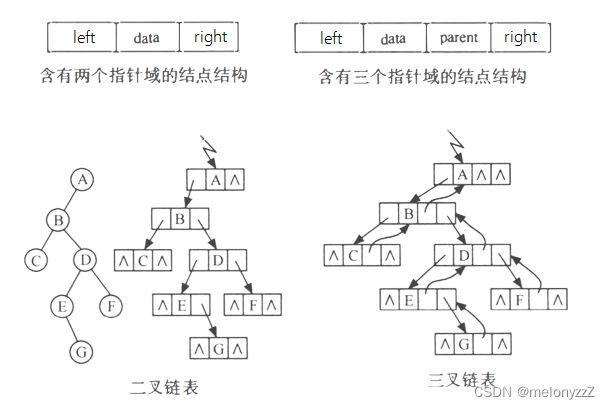
设计不同的结点结构可以构成不同形式的链式存储结构。根据二叉树的定义，二叉树的链表中的结点至少包含 3 个域：数据域和左、右指针域。有时，为了便于找到结点的双亲，还在结点结构中增加一个指向其双亲结点的指针域。利用这两种结点结构所得二叉树的存储结构分别称之为二叉链表和三叉链表。
// 二叉树的二叉链表存储表示
typedef struct BiTNode
{
DataType data; // 结点数据域
struct BiTNode* left; // 左孩子指针
struct BiTNode* right; // 右孩子指针
}BiTNode;
// 二叉树的三叉链表存储表示
typedef struct BiTNode
{
DataType data; // 结点数据域
struct BiTNode* left; // 左孩子指针
struct BiTNode* right; // 右孩子指针
struct BiTNode* parent; // 双亲结点指针
}BiTNode;以下的二叉树遍历及其应用的算法均采用二叉链表形式实现，而在更后面的学习中，例如红黑树，则会用到三叉链表。
3.1 - 遍历二叉树
遍历二叉树（traversing binary tree）是指按某条搜索路径巡访树中每个结点，使得每个结点均被访问一次，而且仅被访问一次。
访问的含义很广，可以是对结点做各种处理，包括输出结点的信息，对结点进行运算和修改等。
遍历二叉树是二叉树最基本的操作，也是二叉树其他各种操作的基础，遍历的实质是对二叉树进行线性化的过程，即遍历的结果是将非线性结构的树中结点排成一个线性序列。
根据根结点的访问顺序，有以下三种遍历。
-
先序（根）遍历：
若二叉树为空，则空操作；否则
(1) 访问根结点；
(2) 先序遍历左子树；
(3) 先序遍历右子树。
-
中序（根）遍历：
若二叉树为空，则空操作；否则
(1) 中序遍历左子树；
(2) 访问根结点；
(3) 中序遍历右子树；
-
后序（根）遍历：
若二叉树为空，则空操作；否则
(1) 后序遍历左子树；
(2) 后序遍历右子树；
(3) 访问根结点。
3.1.1 - 递归算法
先序遍历的递归算法：
void PreOrder(BiTNode* root)
{
if (root == NULL)
{
return;
}
visit(root);
PreOrder(root->left);
PreOrder(root->right);
}中序遍历的递归算法：
void InOrder(BiTNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
visit(root);
InOrder(root->right);
}后序遍历的递归算法：
void PostOrder(BiTNode* root)
{
if (root == NULL)
{
return;
}
PostOrder(root->left);
PostOrder(root->right);
visit(root);
}3.1.2 - 非递归算法
可以借助栈将递归算法改写成非递归算法。
先序遍历的非递归算法：
void PreOrder(BiTNode* root)
{
Stack st;
StackInit(&st); // 初始化一个空栈
BiTNode* cur = root;
while (cur || !StackEmpty(&st))
{
while (cur)
{
visit(cur);
StackPush(&st, cur);
cur = cur->left;
}
BiTNode* top = StackTop(&st);
StackPop(&st);
cur = top->right;
}
StackDestroy(&st);
}中序遍历的非递归算法：
void InOrder(BiTNode* root)
{
Stack st;
StackInit(&st); // 初始化一个空栈
BiTNode* cur = root;
while (cur || !StackEmpty(&st))
{
while (cur)
{
StackPush(&st, cur);
cur = cur->left;
}
BiTNode* top = StackTop(&st);
StackPop(&st);
visit(top);
cur = top->right;
}
StackDestroy(&st);
}后序遍历的非递归算法：
void PostOrder(BiTNode* root)
{
Stack st;
StackInit(&st); // 初始化一个空栈
BiTNode* cur = root;
BiTNode* prev = NULL;
while (cur || !StackEmpty(&st))
{
while (cur)
{
StackPush(&st, cur);
cur = cur->left;
}
BiTNode* top = StackTop(&st);
if (top->right && top->right != prev)
{
cur = top->right;
}
else
{
StackPop(&st);
visit(top);
prev = top;
}
}
StackDestroy(&st);
}3.1.3 - 层序遍历
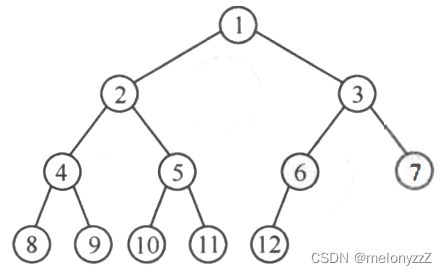
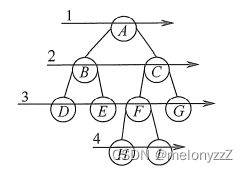
下图为二叉树的层序遍历，即按照箭头所指方向，按照 1, 2, 3, 4 的层次顺序，对二叉树的各个结点进行访问。
算法步骤：
-
初始化一个空队列。
-
若根结点非空，则根结点入队。
-
若队列非空，则队头结点出队，并访问该结点。若它有左子树，则将左子树根结点入队；若它有右子树，则将右子树根结点入队。
-
重复步骤 3，直至队列为空。
void LevelOrder(BiTNode* root)
{
Queue q;
QueueInit(&q); // 初始化一个空队列
if (root)
{
QueuePush(&q, root); // 若根结点非空，则根结点入队
}
while (!QueueEmpty(&q))
{
BiTNode* front = QueueFront(&q);
QueuePop(&q); // 队头结点出队
visit(front); // 访问队头结点
if (front->left != NULL)
{
QueuePush(&q, front->left); // 左子树不为空，则左子树的根结点入队
}
if (front->right != NULL)
{
QueuePush(&q, front->right); // 右子树不为空，则右子树的根结点入队
}
}
QueueDestroy(&q);
}判断一棵二叉树是否为完全二叉树：
bool IsCompleteBiTree(BiTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BiTNode* front = QueueFront(&q);
QueuePop(&q); // 队头结点出队
if (front == NULL)
{
break;
}
else
{
// 出队结点的左右孩子（可能为空）入队
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
while (!QueueEmpty(&q))
{
// 如果是完全二叉树，遇到空则表明最后一个叶子结点已经出队，队列中只剩下空指针
BiTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}3.2 - 二叉树遍历算法的应用
遍历" 是二叉树各种操作的基础，假设访问结点的具体操作不仅仅局限于输出结点的数据域的值，而把 "访问" 延伸到对结点的判别、计数等其他操作，可以解决一些关于二叉树的其他实际问题。
3.2.1 - #号法创建二叉树
方法一：
void BiTreeCreate(BiTNode** prt)
{
char ch = 0;
scanf("%c", &ch);
if (ch == '#') // 表明是空树
{
*prt = NULL;
}
else
{
*prt = (BiTNode*)malloc(sizeof(BiTNode));
(*prt)->data = ch;
BiTreeCreate(&(*prt)->left); // 递归创建左子树
BiTreeCreate(&(*prt)->right); // 递归创建右子树
}
}方法二：
BiTNode* BiTreeCreate(char* pre, int* pi)
{
if (pre[*pi] == '#')
{
(*pi)++;
return NULL;
}
BiTNode* root = (BiTNode*)malloc(sizeof(BiTNode));
root->data = pre[(*pi)++];
root->left = BiTreeCreate(pre, pi);
root->right = BiTreeCreate(pre, pi);
return root;
}3.2.2 - 复制二叉树
void BiTreeCopy(BiTNode* root, BiTNode** prt)
{
if (root == NULL)
{
*prt = NULL;
}
else
{
*prt = (BiTNode*)malloc(sizeof(BiTNode));
(*prt)->data = root->data; // 复制根结点
BiTreeCopy(root->left, &(*prt)->left); // 递归复制左子树
BiTreeCopy(root->right, &(*prt)->right); // 递归复制右子树
}
}3.2.3 - 计算二叉树的深度
int BiTreeDepth(BiTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftDepth = BiTreeDepth(root->left); // 递归计算左子树的深度
int rightDepth = BiTreeDepth(root->right); // 递归计算右子树的深度
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}切不可直接写成
return BiTreeDepth(root->left) > BiTreeDepth(root->right) ? BiTreeDepth(root->left) + 1 ? BiTreeDepth(root->right) + 1;。
3.2.4 - 统计二叉树中结点个数
统计二叉树中的结点个数：
int BiTNodeCount(BiTNode* root)
{
if (root == NULL)
{
return 0;
}
return 1 + BiTNodeCount(root->left) + BiTNodeCount(root->right);
}统计二叉树中叶子结点的个数：
int BiTLeafCount(BiTNode* root)
{
if (root == NULL)
return 0;
else if (root->left == NULL && root->right == NULL)
return 1;
else
return BiTLeafCount(root->left) + BiTLeafCount(root->right);
}统计二叉树中度为 1 的结点个数：
int BiTNodeOneCount(BiTNode* root)
{
if (root == NULL)
return 0;
else if ((root->left == NULL && root->right) || (root->left && root->right == NULL))
return 1 + BiTNodeOneCount(root->left) + BiTNodeOneCount(root->right);
else
return BiTNodeOneCount(root->left) + BiTNodeOneCount(root->right);
}统计二叉树中度为 2 的结点个数：
int BiTNodeTwoCount(BiTNode* root)
{
if (root == NULL)
return 0;
else if (root->left && root->right)
return 1 + BiTNodeTwoCount(root->left) + BiTNodeTwoCount(root->right);
else
return BiTNodeTwoCount(root->left) + BiTNodeTwoCount(root->right);
}统计二叉树中第 k 层的结点个数：
int BiTLevelKCount(BiTNode* root, int k)
{
if (root == NULL)
return 0;
else if (k == 1)
return 1;
else
return BiTLevelKCount(root->left, k - 1) + BiTLevelKCount(root->right, k - 1);
}3.2.5 - 查找二叉树中的结点
BiTNode* BiTreeFind(BiTNode* root, TDataType x)
{
if (root == NULL || root->data == x)
{
return root;
}
BiTNode* leftRet = BiTreeFind(root->left, x);
if (leftRet != NULL)
{
return leftRet;
}
return BiTreeFind(root->right, x);
}3.2.6 - 销毁二叉树
void BiTreeDestroy(BiTNode* root)
{
if (root == NULL)
return;
BiTreeDestroy(root->left);
BiTreeDestroy(root->right);
free(root);
}因为是传值调用，修改形参不会影响实参，所以需要在函数外部手动将根结点指针置为空，即
BiTreeDestroy(root); root = NULL。还需要注意的是，不能先销毁根结点，然后再销毁根结点的左、右子树，除非提前记录左、右子树根结点的指针。