5047. 多边形三角剖分的最低得分

5047. 多边形三角剖分的最低得分

转载请注明出处
附上我的博客链接 四元君
题目难度 Medium

题目描述

给定 N，想象一个凸 N 边多边形，其顶点按顺时针顺序依次标记为 A[0], A[i], …, A[N-1]。

假设您将多边形剖分为 N-2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

示例 1：

输入：[1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

输入：[3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

输入：[1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

3 <= A.length <= 50
1 <= A[i] <= 100

解法

基本的思路是动态规划。

假设我们现在有一个六边形，我们用cost[i][j]存储由第i号顶点到第j号顶点所划定的三角形的值之和。如下图：

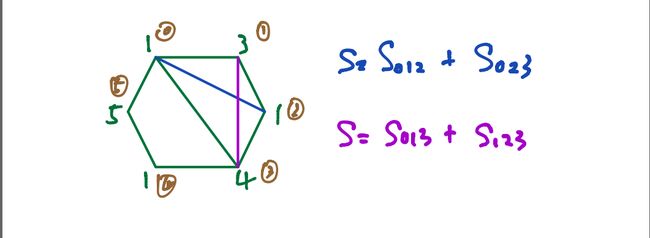
比如说我们选定cost[0][3]，他表示从0号顶点到3号顶点的所有右侧的三角形值的和（右侧是我们的顺时针方向）。这个值的和可以有两种算法，一种是蓝色的S012+S023;一种是紫色的S013+S123。我们将所有的计算的值存储在一张表中，如下图：

将cost[i][i+1]的对角线初始化为0，意义为两个重合点无法构成三角形；cost[i][i+2]对角线初始化为由i，i+1，i+2三点构成的三角形的值。

此后更新步长step，美更新一次意味着划定的区域多加入一个三角形，新的值由新的三角形面积和老的三角形面积共同决定，核心公式为：

cost[当前目标] = min (cost[当前目标], cost[细分后三角形A] + cost[细分后三角形B]+ A[i] * A[j] * A[k]);

即

cost[i][j] = min (cost[i][j], cost[i][k] + cost[k][j]+ A[i] * A[j] * A[k]);

完整代码如下：

class Solution {
public:
    int cost[100][100];
    int minScoreTriangulation(vector& A) {
        int n = A.size();
        for (int i = 0;i < n; ++ i) {
            for (int j = 0;j < n; ++ j) {
                cost[i][j] = INT_MAX;
            }
        }
        for (int i = 0;i < n - 1; ++ i) {
            cost[i][i + 1] = 0;
        }
        
        for (int step = 2; step < n; ++ step) {
            for (int i = 0;i + step < n; ++ i) {
                int j = i + step;
                for (int k = i + 1;k <= j - 1; ++ k) {
                    cost[i][j] = min (cost[i][j], cost[i][k] + cost[k][j]+ A[i] * A[j] * A[k]);
                }
            }
        }
        return cost[0][n-1];
    }
};