CRC（循环冗余校验）

在数据传输过程中，无论传输系统的设计再怎么完美，差错总会存在，这种差错可能会导致在链路上传输的一个或者多个帧被破坏(出现比特差错，0变为1，或者1变为0)，从而接受方接收到错误的数据。为尽量提高接受方收到数据的正确率，在接收方接收数据之前需要对数据进行差错检测，当且仅当检测的结果为正确时接收方才真正收下数据。检测的方式有多种，常见的有奇偶校验、因特网校验和循环冗余校验等。循环冗余校验是一种用于校验通信链路上数字传输准确性的计算方法（通过某种数学运算来建立数据位和校验位的约定关系的 [1]  ）。发送方计算机使用某公式计算出被传送数据所含信息的一个值，并将此值 附在被传送数据后，接收方计算机则对同一数据进行 相同的计算，应该得到相同的结果。如果这两个 CRC结果不一致，则说明发送中出现了差错，接收方计算机可要求发送方计算机重新发送该数据。

在计算机网络通信中运用CRC校验时相对于其他校验方法就有一定的优势。CRC可以高比例的纠正信息传输过程中的错误，可以在极短的时间内完成数据校验码的计算，并迅速完成纠错过程，通过数据包自动重发的方式使得计算机的通信速度大幅提高，对通信效率和安全提供了保障。由于 CRC 算法检验的检错能力极强，且检测成本较低，因此在对于编码器和电路的检测中使用较为广泛。从检错的正确率与速度、成本等方面，都比奇偶校验等校验方式具有优势。因而，CRC 成为计算机信息通信领域最为普遍的校验方式。

工作原理

 1. CRC校验原理

      CRC校验原理看起来比较复杂，好难懂，因为大多数书上基本上是以二进制的多项式形式来说明的。其实很简单的问题，其根本思想就是先在要发送的帧后面附加一个数（这个就是用来校验的校验码，但要注意，这里的数也是二进制序列的，下同），生成一个新帧发送给接收端。当然，这个附加的数不是随意的，它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除（注意，这里不是直接采用二进制除法，而是采用一种称之为“模2除法”）。到达接收端后，再把接收到的新帧除以（同样采用“模2除法”）这个选定的除数。因为在发送端发送数据帧之前就已通过附加一个数，做了“去余”处理（也就已经能整除了），所以结果应该是没有余数。如果有余数，则表明该帧在传输过程中出现了差错。

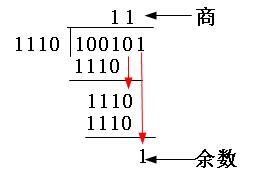
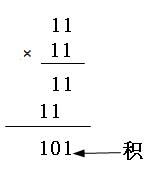
      【说明】“模2除法”与“算术除法”类似，但它既不向上位借位，也不比较除数和被除数的相同位数值的大小，只要以相同位数进行相除即可。模2加法运算为：1+1=0，0+1=1，0+0=0，无进位，也无借位；模2减法运算为：1-1=0，0-1=1，1-0=1，0-0=0，也无进位，无借位。相当于二进制中的逻辑异或运算。也就是比较后，两者对应位相同则结果为“0”，不同则结果为“1”。如100101除以1110，结果得到商为11，余数为1，如图5-9左图所示。如11×11=101，如图5-9右图所示。

 

 　　　　　　　　　　图5-9 “模2除法”和“模2乘法”示例

     具体来说，CRC校验原理就是以下几个步骤：

   （1）先选择（可以随机选择，也可按标准选择，具体在后面介绍）一个用于在接收端进行校验时，对接收的帧进行除法运算的除数（是二进制比较特串，通常是以多项方式表示，所以CRC又称多项式编码方法，这个多项式也称之为“生成多项式”）。

   （2）看所选定的除数二进制位数（假设为k位），然后在要发送的数据帧（假设为m位）后面加上k-1位“0”，然后以这个加了k-1个“0“的新帧（一共是m+k-1位）以“模2除法”方式除以上面这个除数，所得到的余数（也是二进制的比特串）就是该帧的CRC校验码，也称之为FCS（帧校验序列）。但要注意的是，余数的位数一定要是比除数位数只能少一位，哪怕前面位是0，甚至是全为0（附带好整除时）也都不能省略。

   （3）再把这个校验码附加在原数据帧（就是m位的帧，注意不是在后面形成的m+k-1位的帧）后面，构建一个新帧发送到接收端，最后在接收端再把这个新帧以“模2除法”方式除以前面选择的除数，如果没有余数，则表明该帧在传输过程中没出错，否则出现了差错。

    通过以上介绍，大家一定可以理解CRC校验的原理，并且不再认为很复杂吧。

    从上面可以看出，CRC校验中有两个关键点：一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串（或多项式）；二是把原始帧与上面选定的除进行二进制除法运算，计算出FCS。前者可以随机选择，也可按国际上通行的标准选择，但最高位和最低位必须均为“1”，如在IBM的SDLC（同步数据链路控制）规程中使用的CRC-16（也就是这个除数一共是17位）生成多项式g（x）= x16 + x15 + x2 +1（对应二进制比特串为：11000000000000101）；而在ISO HDLC（高级数据链路控制）规程、ITU的SDLC、X.25、V.34、V.41、V.42等中使用CCITT-16生成多项式g（x）=x16 + x15 + x5 +1（对应二进制比特串为：11000000000100001）。

       2.    CRC校验码的计算示例

      由以上分析可知，既然除数是随机，或者按标准选定的，所以CRC校验的关键是如何求出余数，也就是CRC校验码。

    下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G（X） = X4 + X3 + 1，要求出二进制序列10110011的CRC校验码。下面是具体的计算过程：

   （1）首先把生成多项式转换成二进制数，由G（X） = X4 + X3 + 1可以知道（，它一共是5位（总位数等于最高位的幂次加1，即4+1=5），然后根据多项式各项的含义（多项式只列出二进制值为1的位，也就是这个二进制的第4位、第3位、第0位的二进制均为1，其它位均为0）很快就可得到它的二进制比特串为11001。

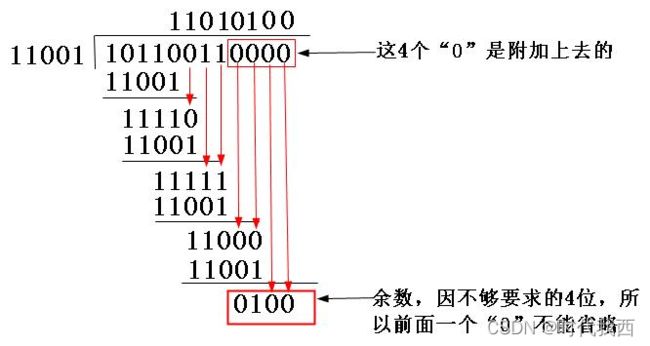
   （2）因为生成多项式的位数为5，根据前面的介绍，得知CRC校验码的位数为4（校验码的位数比生成多项式的位数少1）。因为原数据帧10110011，在它后面再加4个0，得到101100110000，然后把这个数以“模2除法”方式除以生成多项式，得到的余数，即CRC校验码为0100，如图5-10所示。注意参考前面介绍的“模2除法”运算法则。

 

                                      图5-10 CRC校验码计算示例

    （3）把上步计算得到的CRC校验码0100替换原始帧101100110000后面的四个“0”，得到新帧101100110100。再把这个新帧发送到接收端。

    （4）当以上新帧到达接收端后，接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除，验证余数是否为0，如果为0，则证明该帧数据在传输过程中没有出现差错，否则出现了差错。

    通过以上CRC校验原理的剖析和CRC校验码的计算示例的介绍，大家应该对这种看似很复杂的CRC校验原理和计算方法应该比较清楚了。