数据结构与算法学习笔记——二叉树遍历（一）（递归、迭代）

最近学习二叉树相关的内容，个人认为其中最重要的应该就是二叉树的遍历了，包括先序，中序，后续。通常二叉树的遍历有三种方法：递归、迭代和Morris遍历。递归应该是最容易理解了， Morris遍历最难理解。关于Morris遍历后面会单独再整理。

节点的定义

struct Node{
    int data;
    Node *parent, *left, *right;
    Node(int v = 0,Node *p = NULL, Node* l = NULL, Node* r = NULL ): data(v), parent(p), left(l), right(r){}
    Node* insertAsLC( const int &e){//insert left child
        return left = new Node(e, this) ;
    }
    Node* insertAsRC(const int &e){//insert right child
        return right = new Node(e, this);
    }
};

用struct定义一个Node类，类中成员都为public,包括了构造函数和插入左右节点的成员函数。

二叉树的定义

class Tree{
    private:
        Node *root;
        int _size;

        void RecursionInorder(Node *root);
	void RecursionPreorder(Node *root);
	void RecursionPostorder(Node *root);

	void StackInorder(Node *root);
	void StackPreorder(Node *root);
	void StackPostorder(Node *root);

	void MorrisReverse(Node *from, Node *to);
	void MorrisPrintReverse(Node *from, Node *to);
     public:
        Tree(Node *r = NULL, int s = 0): root(r), _size(s){}
        void buildTree(const vector &L);
        void printTree();
	void printTree_level();
	//recursion traversal		
	void RecursionInorder();
	void RecursionPreorder();
	void RecursionPostorder();
	//stack iteration traversal
	void StackInorder();
	void StackPreorder();
	void StackPostorder();
	//Morris traversal
	void MorrisInorder();
	void MorrisPreorder();
	void MorrisPostorder();
};

Tree类中定义了树根 root，树的规模 _size, 私有成员中包含了一些私有成员函数，他们的作用是被相应的public成员函数调用，目的是为了统一接口。首先是通过vector中的数据随意构造了一个树，并打印出来。随后就是一系列的遍历操作。包括了递归遍历，迭代遍历，Morris遍历。下面分别解释。

构造二叉树，并打印：

void Tree::buildTree(const std::vector &L){
    if(L.empty())
        return ;
    std::queue parentQueue;
    std::queue childQueue;

    root = new Node(L[0]);
	++_size;
    parentQueue.push(root);

    std::size_t times = 1;
    while(times < L.size()){
        Node *parent = parentQueue.front();
        parentQueue.pop();
        
        parent->insertAsLC(L[times++]);
		++_size;
        childQueue.push(parent->left);
        
        if(times == L.size())
            break;

        parent->insertAsRC(L[times++]);
		++_size;
        childQueue.push(parent->right);
        
        if(parentQueue.empty()){
            parentQueue = childQueue;
            std::queue empty;
            std::swap(childQueue, empty);
        }
       
    }    
}

void Tree::printTree(){

    Node *node = root;
    std::queue temp1;
    std::queue temp2;

    temp1.push(node);

    while(!temp1.empty()){
        node = temp1.front();
        if(node->left != NULL)
            temp2.push(node->left);
        if(node->right != NULL)
            temp2.push(node->right);

        temp1.pop();

        std::cout << node->data << " ";
        if(temp1.empty()){
            std::cout << std::endl;
            temp1 = temp2;
            std::queue empty;
            std::swap(temp2, empty);
        }
    }

}

在树的构造函数中用了两个队列，一层一层从左到右构造二叉树，同理打印树的个节点。

递归遍历二叉树

先序遍历的顺序是：根->左子树->右子树；

中序遍历的顺序是：左子树->根->右子树；

后续遍历的顺序是：左子树->右子树->根；

//recursion traversal
void Tree::RecursionInorder(Node *root){
	if(root == NULL)
		return;
	RecursionInorder(root->left);
	cout << root->data << " ";
	RecursionInorder(root->right);
}
void Tree::RecursionPreorder(Node *root){
	if(root == NULL)
		return;
	cout << root->data << " ";
	RecursionPreorder(root->left);	
	RecursionPreorder(root->right);
}
void Tree::RecursionPostorder(Node *root){
	if(root == NULL)
		return;	
	RecursionPostorder(root->left);	
	RecursionPostorder(root->right);
	cout << root->data << " ";
}
void Tree::RecursionInorder(){
	RecursionInorder(root);
}
void Tree::RecursionPreorder(){
	RecursionPreorder(root);
}
void Tree::RecursionPostorder(){
	RecursionPostorder(root);
}

以上代码应该很好理解。

迭代遍历二叉树

递归的本质是利用函数调用栈进行的，以下的迭代法是用自己构造的栈来存储节点并使之能按照我们想要的顺序访问节点。

先序遍历是首先把根节点入栈，然后在每次循环中执行：

1，此时的栈顶元素是当前的根节点，访问并弹出栈顶节点；

2，把当前节点的右左孩子节点分别入栈（右孩子先入栈，左孩子后入栈，为了以后左孩子能先弹出栈）；

反复执行 1 和 2 操作，直到栈变空。

代码如下：

void Tree::StackPreorder(Node *root){
	stack childStack;
	if(root == NULL)
		return;
	Node* cur = root;
	childStack.push(cur);
	while(!childStack.empty()){
		cur = childStack.top();
		childStack.pop();
		cout << cur->data << " ";
		if(cur->right != NULL)
			childStack.push(cur->right);
		if(cur->left != NULL)
			childStack.push(cur->left);
	}
}

中序遍历是先要找到第一个访问的节点（应该是整个树最左边的节点），同时将所有祖先节点入栈。因此当前节点的祖先节点都存储在了栈中，当前节点访问完以后就弹出栈顶节点（为已访问节点的父节点），访问完以后就进入右子树，在右子树中同样需要找到访问入口，原理同上描述。具体操作如下：

首先定义一个临时变量存储根节点，并将根节点入栈，在每次循环中执行：

1，从根节点一直向左下寻找，并将经过的节点入栈，直到某节点的左孩子为空，则该点就是访问入口；

2，从栈顶访问并弹出该节点，然后访问该节点的右子树，将右孩子节点赋值给临时节点，返回上一步操作；

直到栈变空。

代码如下：

void Tree::StackInorder(Node *root){
	stack parentStack;
	if(root == NULL)
		return;
	Node* cur = root;
	while(cur != NULL || !parentStack.empty()){
		if(cur != NULL){
			parentStack.push(cur);
			cur = cur->left;
		}else{
			cur = parentStack.top();
			parentStack.pop();
			cout << cur->data << " ";
			cur = cur->right;
		}
	}	
}

后序遍历，通常有两种做法，一种是常规的借用一个栈来存储节点控制访问顺序；另一种的借助先序遍历，借助两个栈来实现后续遍历，这里介绍的就是这个方法。

后序遍历的顺序的：左->右->根，而之前先序遍历的顺序是：根->左->右，并且我们在先序遍历中强调的左右孩子节点入栈的顺序（先右入后左入），倘若我们先把左子树入栈再把右子树入栈，那么我们得到的遍历顺序就变成了：根->右->左，这个顺序敲好和后续遍历的顺序相反，于是我们在借助一个栈就可以实现 左->右->根 的后续遍历顺序了。

代码如下：

void Tree::StackPostorder(Node *root){
	stack inStack, outStack;	
	if(root == NULL)
		return;
	Node *cur = root;
	inStack.push(cur);
	while(!inStack.empty()){
		cur = inStack.top();
		inStack.pop();
		outStack.push(cur);
		if(cur->left != NULL)
			inStack.push(cur->left);
		if(cur->right != NULL)
			inStack.push(cur->right);
	}
	while(!outStack.empty()){
		cout << outStack.top()->data << " ";
		outStack.pop();
	}

}

以下代码用于同一接口：

void Tree::StackInorder(){
	StackInorder(root);
}
void Tree::StackPreorder(){
	StackPreorder(root);
}
void Tree::StackPostorder(){
	StackPostorder(root);
}

主函数

以下是主函数：

#include
#include
#include"BinTree.h"
using namespace std;
int main(){

    vector v;
    for(int i = 0; i < 21; ++i)
        v.push_back(i + 1);
     
    Tree tree;
    tree.buildTree(v);
    tree.printTree();
    tree.printTree_level();
    std::cout << "\n";
    std::cout << "\n-------------Recursion Traversal-----------------";
    std::cout << "\nRecursion Inorder: " << endl;
    tree.RecursionInorder();
    std::cout << "\nRecursion Preorder: " << endl;
    tree.RecursionPreorder();
    std::cout << "\nRecursion Postorder: " << endl;
    tree.RecursionPostorder();
    std::cout << "\n-------------Stack Iteration Traversal------------";
    std::cout << "\nIteration Inorder: " << endl;
    tree.StackInorder();
    std::cout << "\nIteration Preorder: " << endl;
    tree.StackPreorder();
    std::cout << "\nIteration Postorder: " << endl;
    tree.StackPostorder();
    std::cout << endl;
    return 0;  
}

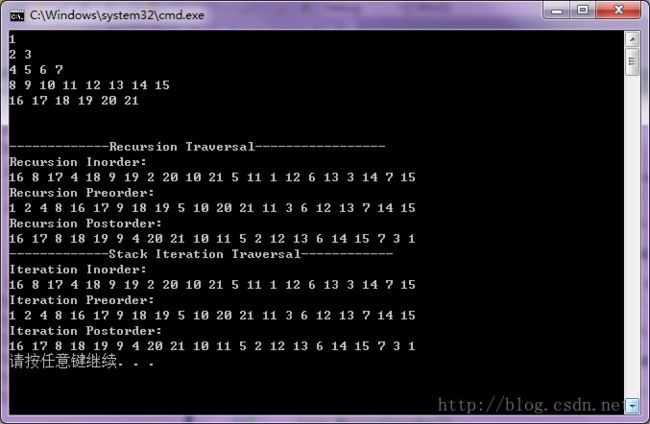
运行结果：