pytroch搭建自编码模型对MNIST数据进行降维和重构

自编码网络模型，也称自动编码器(AutoEncoder),是一种基于无监督学习的数据维度压缩和特征表示方法,目的是对一组数据学习出一种表示。1986年Rumelhart提出自编码模型用于高维复杂数据的降维。由于自动编码器通常应用于无监督学习,所以不需要对训练样本进行标记。自动编码器在图像重构、聚类、降维、自然语言翻译等方面应用广泛

目录

一、自编码模型简介

二、基于线性层的自编码模型

2.1 自编码网络数据准备

 2.2 自编码网络的构建

2.3 自编码网络的训练

2.4 自编码网络的数据重构

2.5 SVM用于编码特征

---

一、自编码模型简介

自编码器是深度学习的研究热点之一，在很多领域都有应用。其应用主要有两个方面，第一是对数据降维，或者降维后对数据进行可视化;第二是对数据进行去噪，尤其是图像数据去噪。
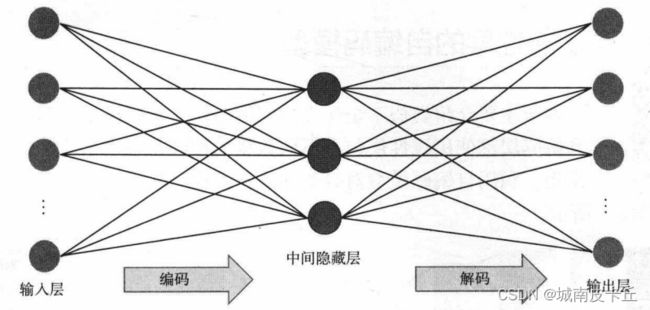
最初的自编码器是一个三层网络结构，即输入层、中间隐藏层和输出层，其中输入层和输出层的神经元个数相同，且中间隐藏层的神经元个数会较少，从而达到降维的目的。其网络结构如下图所示。

自编码模型（三层结构）

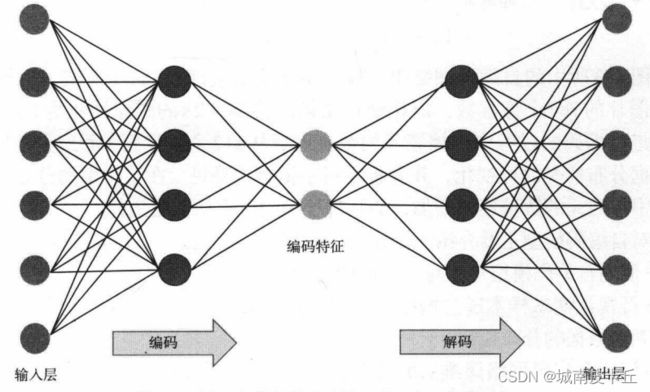
 深度自编码器是将自编码器堆积起来，可以包含多个中间隐藏层。由于其可以有更多的中间隐藏层，所以对数据的表示和编码能力更强，而且在实际应用中也更加常用。其网络结构如下图所示。

深度自编码模型

 稀疏自编码器，是在原有自编码器的基础上，对隐层单元施加稀疏性约束，这样会得到对输人数据更加紧凑的表示，在网络中仅有小部分神经元会被激活。常用的稀疏约束是使用范数约束，目的是让不重要的神经元的权重为0。
卷积自编码器是使用卷积层搭建获得的自编码网络。当输入数据为图像时，由于卷积操作可以从图像数据中获取更丰富的信息，所以使用卷积层作为自编码器隐藏层，通常可以对图像数据进行更好的表示。在实际应用中，用于处理图像的自动编码器的隐藏层几乎都是基于卷积的自动编码器。在卷积自编码器的编码器部分,通常可以通过池化层负责对数据进行下采样，卷积层负责对数据进行表示，而解码器则通常使用可以对特征映射进行上采样的操作来完成。

二、基于线性层的自编码模型

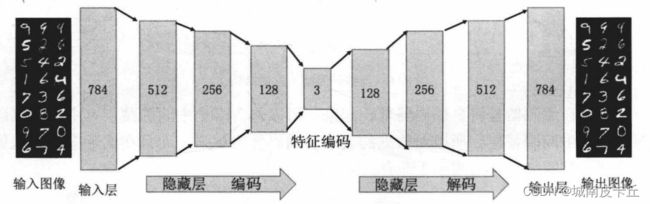
接下来介绍类似于全连接神经网络的自编码模型，即网络中编码层和解码层都使用线性层包含不同数量的神经元来表示。针对手写字体数据集，利用自编码模型对数据降维和重构。基于线性层的自编码模型结构如下图所示：

基于线性层的自编码模型

在上图所示的自编码网络中，输入层和输出层都有784个神经元，对应着一张手写图片的784个像素数，即在使用图像时将28×28的图像转化为1×784的向量。在进行编码的过程中，神经元的数量逐渐从512个减少到3个，主要是便于降维后数据分布情况的可视化，并分析手写字体经过编码后在空间中的分布规律。在解码器中神经元的数量逐渐增加，会从特征编码中重构原始图像。

2.1 自编码网络数据准备

接下来使用自编码模型对手写字体图像进行重构，通过torchvision库中的MNIST（）函数导入训练和测试所需要的数据集——手写字体数据集，并对数据进行预处理,程序如下:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D#用于三维数据可视化
import hiddenlayer as hl
from sklearn.manifold import TSNE
from sklearn.svm import SVC#用于建立支持向量机分类器
from sklearn.decomposition import PCA#对数据进行主成分分析
from sklearn.metrics import classification_report,accuracy_score
import torch
from torch import  nn
import torch.functional as F
import torch.utils.data as Data
import torch.optim  as optim
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid


#使用手写字体，准备训练数据集
train_data=MNIST(
    root="../Dataset",#数据的路径
    train=True,
    transform=transforms.ToTensor(),
    download=False
)
#将图像数据转化为向量数据
train_data_x=train_data.data.type(torch.FloatTensor) / 255.0
train_data_x=train_data_x.reshape(train_data_x.shape[0],-1)
train_data_y=train_data.targets
#定义一个数据加载器
train_laoder=Data.DataLoader(
    dataset=train_data_x,#使用的数据集
    batch_size=64,#批处理样本大小
    shuffle=True,#迭代前打乱数据
    num_workers=0
)
#读测试数据集进行导入
test_data=MNIST(
    root="../Dataset",
    train=False,#只使用训练集数据集
    transform=transforms.ToTensor(),
    download=False
)
#为测试数据添加一个通道维度
test_data_x=test_data.data.type(torch.FloatTensor) /255.0
test_data_x=test_data_x.reshape(test_data_x.shape[0],-1)
test_data_y=test_data.targets

上述程序导人训练数据集后，将训练数据集中的图像数据和标签数据分别保存为train_data_x和train_data_y变量，并且针对训练数据集中的图像将像素值处理在0~1之间，并且将每个图像处理为长784的向量,最后通过Data.DataLoader()函数将训练数据train_data_x处理为数据加载器，此处并没有包含对应的类别标签，这是因为上述自编码网络训练时不需要图像的类别标签数据，在数据加载器中每个batch包含64个样本。针对测试集将其图像和经过预处理后的图像分别保存为test_data_x和test_data_y变量。

可视化训练数据集中一个batch的图像内容，以观察手写体图像的情况，程序如下:

#可视化一个batch的图像内容
for step,b_x in enumerate(train_laoder):
    if step>0:
        break
    im=make_grid(b_x.reshape((-1,1,28,28)))
    im=im.data.numpy().transpose((1,2,0))
    plt.figure()
    plt.imshow(im)
    plt.axis("off")
    plt.show()

上面的程序在获取一个batch数据后，通过make.grid()转换数据，方便对图像数据进行可视。该函数是PyTorch库中的函数，可以直接将数据结构[batch,channel,height, width]形式的batch图像转化为图像矩阵，便于将多张图像进行可视化。上述程序可视化结果如下图所示： 

 2.2 自编码网络的构建

为了搭建一个自编码器网络，需要构建一个EnDecoder()类,程序如下:

class EnDecoder(nn.Module):
    def __init__(self):
        super(EnDecoder, self).__init__()
        #定义Encoder
        self.Encoder=nn.Sequential(
            nn.Linear(784,512),
            nn.Tanh(),
            nn.Linear(512,256),
            nn.Tanh(),
            nn.Linear(256,128),
            nn.Tanh(),
            nn.Linear(128,3),
            nn.Tanh()
        )
        #定义Deconder
        self.Decoder=nn.Sequential(
            nn.Linear(3,128),
            nn.Tanh(),
            nn.Linear(128,256),
            nn.Tanh(),
            nn.Linear(256,512),
            nn.Tanh(),
            nn.Linear(512,784),
            nn.Sigmoid()
        )
    #定义网路的前向传播路径
    def forward(self,x):
        encoder=self.Encoder(x),
        decoder=self.Encoder(x),
        return encoder,decoder
model=EnDecoder()

在上面的程序中，搭建自编码网络时，将网络分为编码器部分Encoder和解码器部分Decoder。编码器部分将数据的维度从784维逐步减少到三维，每个隐藏层使用的激活函数为Tanh激活函数。解码器部分将特征编码从三维逐步增加到784维,除输出层使用Sigmoid激活函数外，其他隐藏层使用Tanh激活函数。在网络的前向传播函数forward()中，输出编码后的结果encoder和解码后的结果decoder.

2.3 自编码网络的训练

使用训练数据对网络中的参数进行训练时，使用torch.optim.Adam()优化器对网络中的参数进行优化，并使用nn.MSELoss()函数定义损失函数，即使用均方根误差损失(因为自编码网络需要重构出原始的手写体数据，所以看作回归问题，即与原始图像的误差越小越好，使用均方根误差作为损失函数较合适，也可以使用绝对值误差作为损失函数)。为了观察网络的训练过程，通过HiddenLayer库将网络在训练数据过程中的损失函数的大小进行动态可视化。网络的训练及可视化程序如下所示:

optimizer=torch.optim.Adam(model.parameters(),lr=0.003)
loss_func=nn.MSELoss()
history=hl.History()
canvas=hl.Canvas()
train_num=0
val_num=0
#对模型进行迭代训练,对所有数据训练epoch轮
for epoch in range(10):
    train_loss_epoch=0
    #对训练数据的加载器进行迭代训练
    for step,b_x in enumerate(train_laoder):
        # 使用每个batch训练模型
        _,output=model(b_x)#在训练batch上的输出
        loss=loss_func(output,b_x)#均方根误差
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        train_loss_epoch+=loss.item() * b_x.size(0)
        train_num=train_num+b_x.size(0)
    #计算一个batch的损失
    train_loss=train_loss_epoch/train_num
    #保存每一个epoch上的输出loss
    history.log(epoch,train_loss=train_loss)
    with canvas:
        canvas.draw_plot(history["train_loss"])

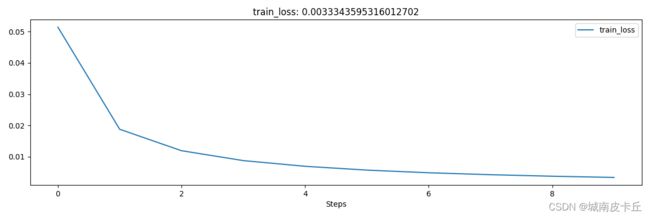
在上面的程序中，计算每个batch的损失函数时，使用loss = loss_func(output,b_x)，其中b_x表示每次网络的输入数据，output表示经过自编码网络的输出内容,即自编码网络的损失是网络重构的图像与输入图像之间的差异，计算两者之间的均方根误差损失。网络在训练过程中损失函数的大小变化情况如图8-5所示，损失函数先迅速减小，然后在一个很小的值上趋于稳定。网络训练结束后，最终的均方根损失约为0.00365。

2.4 自编码网络的数据重构

为了展示自编码网络的效果，可视化一部分测试集经过编码前后的图像，此处使用测试集的前100张图像，程序如下所示:

model.eval()
_,test_decoder=model(test_data_x[0:100,:])
#可视化原始图像
plt.figure(figsize=(6,6))
for i in range(test_decoder.shape[0]):
    plt.subplot(10,10,i+1)
    im=test_data_x[i,:]
    im=im.data.numpy().reshape(28,28)
    plt.imshow(im,cmap=plt.cm.gray)
    plt.axis("off")
plt.show()
#可视化编码后的图像
plt.figure(figsize=(6,6))
for i in range(test_decoder.shape[0]):
    plt.subplot(10,10,i+1)
    im=test_decoder[i,:]
    im=im.data.numpy().reshape(28,28)
    plt.imshow(im,cmap=plt.cm.gray)
    plt.axis("off")
plt.show()

在上面的程序首先使用edmodel.eval（）进入验证模式，通过“_,test_decoder = model(test_data_x[0:100,:])”获取测试集前100张图像在经过网络后的解码器输出结果test_decoder。在可视化时分别先可视化原始的图像，再可视化经过自编码网络后的图像，得到如下图所示的图像。

 对比上图，自编码网络很好地重构了原始图像的结构,但不足的是自编码网络得到的图像有些模糊，而且针对原始图像中的某些细节并不能很好地重构，如某些手写体不规范的4会重构为9等。这是因为在网络中,自编码器部分最后一层只有3个神经元，将784维的数据压缩到三维，会损失大量的信息,故重构的效果会有一些模糊和错误。这里降到三维主要为了方便数据可视化,在实际情况中，可以使用较多的神经元，保留更丰富的信息。

2.5 SVM用于编码特征

自编码网络的另一个作用就是对数据进行降维，保留数据中主要信息的同时,减少数据的维度。当使用其他机器学习方法对特征编码进行分类时，自编码网络的作用是特征提取和变换的模型。下面使用自编码降维，将得到的特征与SVM分类器结合，或者使用主成分分析(PCA)降维到相同的维度与SVM分类器结合，将这两种不同的数据降维方式的效果进行对比，以确定哪种降维对数据分类更有效。

#对训练集和测试集通过自编码网络提取对应特征编码，并且将数据从张量转化为数组。
trained_x,_=model(train_data_x)
trained_x=trained_x.data.numpy()
train_y=train_data_y.data.numpy()
tested_x,_=model(test_data_x)
tested_x=tested_x.data.numpy()
test_y=test_data_y.data.numpy()
#针对主成分降维，用sklearn库中的PCA()函数，只保留3个主成分
pcamodel=PCA(n_components=3,random_state=10)
train_pca_x=pcamodel.fit_transform(train_data_x.data.numpy())
test_pca_x=pcamodel.transform(test_data_x.data.numpy())

在数据准备好后，分别针对两种类型的数据使用相同的参数,建立支持向量机分类器。先对自编码网络降维的数据建立分类器，使用训练集trained_x和train_y对SVM分类器进行训练，然后利用测试集测试SVM分类器的分类精度，并使用accuracy_score()函数和classification_report()函数输出分类器在测试集上的预测效果，程序和结果如下所示:

#使用自编码数据建立分类器，训练和预测
encodersvc=SVC(kernel="rbf",random_state=123)
encodersvc.fit(trained_x,train_y)
edsvc_pre=encodersvc.predict(tested_x)
print(classification_report(test_y,edsvc_pre))
print("模型精度(自编码+SVM):",accuracy_score(test_y,edsvc_pre))

#使用PCA建立分类器
pcasvc=SVC(kernel="rbf",random_state=123)
pcasvc.fit(train_pca_x,train_y)
pcasvc_pre=pcasvc.predict(test_pca_x)
print(classification_report(test_y,pcasvc_pre))
print("模型精度(PCA+SVM):",accuracy_score(test_y,pcasvc_pre))

                precision    recall  f1-score   support
           0       0.93      0.96      0.94       980
           1       0.96      0.98      0.97      1135
           2       0.96      0.88      0.92      1032
           3       0.83      0.90      0.86      1010
           4       0.87      0.81      0.84       982
           5       0.87      0.81      0.84       892
           6       0.93      0.94      0.94       958
           7       0.94      0.91      0.92      1028
           8       0.83      0.84      0.83       974
           9       0.79      0.84      0.81      1009
    accuracy                           0.89     10000
   macro avg       0.89      0.89      0.89     10000
weighted avg       0.89      0.89      0.89     10000
模型精度(自编码+SVM): 0.8901

上面结果显示，用自编码特征建立的SVM分类器在测试集上的预测精度为89.01%。而且每类数据的识别精度都很高，只有数字9、数字4和数字3的识别精度较低。 

                 precision    recall  f1-score   support
           0       0.68      0.74      0.71       980
           1       0.93      0.95      0.94      1135
           2       0.51      0.49      0.50      1032
           3       0.65      0.64      0.64      1010
           4       0.41      0.55      0.47       982
           5       0.42      0.31      0.36       892
           6       0.38      0.60      0.47       958
           7       0.52      0.51      0.52      1028
           8       0.41      0.26      0.32       974
           9       0.44      0.30      0.36      1009
    accuracy                           0.54     10000
   macro avg       0.54      0.53      0.53     10000
weighted avg       0.54      0.54      0.54     10000
模型精度(PCA+SVM): 0.5426 

 从输出结果中可以发现，使用PCA降维后训练得到的SVM分类器，预测精度只有54.26%，其精度比使用自编码网络得到的特征而训练的分类器精度低很多。而且.每类数据的识别精度都不高，只有数字1的识别精度较高，超过了90%。