新视角合成 (Novel View Synthesis)

0.引言

• 辅助理解Nerf

• 摘抄自这里，抄一遍读一遍吧。这个讲的是真浅显易懂。

1.任务定义

1.1.任务定义

新视角合成任务 (Novel View Synthesis) 指的是给定源图像 (Source Image) 及源姿态 (Source Pose)，以及目标姿态 (Target Pose)，渲染生成目标姿态对应的的图片 (Target Image)。新视角合成在 3D 重建、AR/VR 等领域有着广泛的应用。

1.2.坐标变换

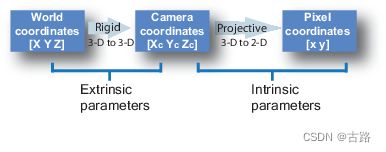
源图像 (Source Image) 好理解，但是源姿态 (Source Pose)指的是什么呢？答案是从相机坐标转换为世界坐标的变换矩阵。这就涉及到 2D 和 3D 之间的坐标转换。下面介绍一下对应的概念：

如上图所示，一共有三个坐标系：

世界坐标系（world coordinate）：表示物理上的三维世界
相机坐标系（camera coordinate）：表示虚拟的三维相机坐标
图像坐标系（pixel coordinate）：表示二维的图片坐标

相机坐标系中的坐标 ${\left[X_c,Y_c,Z_c\right]}^T$ 和三维世界的坐标 $[X,Y,Z{]}^T$ 和之间存在这如下的转换关 系：
[ X c Y c Z c 1 ] = [ r 11 r 12 p 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z 0 0 0 1 ] [ X Y Z 1 ] \left[\begin{array}{l} X_c \\ Y_c \\ Z_c \\ 1 \end{array}\right]=\left[\begin{array}{llll} r_{11} & r_{12} & p_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}\right] ​Xc​Yc​Zc​1​ ​= ​r11​r21​r31​0​r12​r22​r32​0​p13​r23​r33​0​tx​ty​tz​1​ ​ ​XYZ1​ ​
右边的矩阵 C e x = [ r 11 r 12 p 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z 0 0 0 1 ] C_{e x}=\left[\begin{array}{llll}r_{11} & r_{12} & p_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1\end{array}\right] Cex​= ​r11​r21​r31​0​r12​r22​r32​0​p13​r23​r33​0​tx​ty​tz​1​ ​ 是一个仿射变换矩阵, 也叫相机的外参矩阵 (camera extrinsic)。 [ r 11 r 12 p 13 r 21 r 22 r 23 r 31 r 32 r 33 ] \left[\begin{array}{lll}r_{11} & r_{12} & p_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33}\end{array}\right] ​r11​r21​r31​​r12​r22​r32​​p13​r23​r33​​ ​ 包含旋转信息， [ t x t y t z ] \left[\begin{array}{c}t_x \\ t_y \\ t_z\end{array}\right] ​tx​ty​tz​​ ​ 包含平移信息。一般使用
“OpenCV” 风格的相机坐标系, 其中 $Y$ 轴指向下方（向上矢量指向负 $Y$ 方向）, X轴指向右侧, $Z$ 轴指向图像平面。

$C_{ex}$ 是用于从世界坐标转到相机坐标的。对于 NeRF 这些算法来说, 会提供 $C_{ex}$ 的逆矩阵 $C_{ex}^{\prime }$, 用于从相机坐标转涣到世界坐标，也就是源姿态 (source pose)。

而二维图片的坐标 $[x,y{]}^T$ 和相机坐标系中的坐标 $[U,V,W{]}^T$ 存在下面的转换关系:
[ x y 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X c Y c Z c ] \left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X_c \\ Y_c \\ Z_c \end{array}\right] ​xy1​ ​= ​fx​00​0fy​0​cx​cy​1​ ​ ​Xc​Yc​Zc​​ ​
其中, 矩阵 [ f x 0 c x 0 f y c y 0 0 1 ] \left[\begin{array}{ccc}f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{array}\right] ​fx​00​0fy​0​cx​cy​1​ ​ 指的是相机的内参, 包含焦距 (focal length) $\left(f_x,f_y\right)$ 以及图像中 心点的坐标 $\left(c_x,c_y\right)$ 。对于相同的数据集, 相机的内参矩阵一般是固定的, 一般会在一个叫 intrinsics.txt 的文件里面给出。

在介绍了数据集的组成后，新视角合成的任务也可以从机器学习的角度理解为：从一些<图片，相机矩阵>构成的训练集中训练模型，测试时给一个训练集中没有的相机矩阵，模型能预测出对应的图片。

Novel View Synthesis 流程图

1.3.训练流程

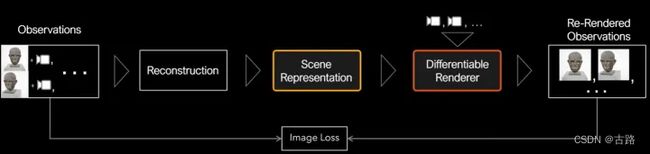
常见的新视角生成的方法的训练步骤可以看由两大步组成：

1）重建: 从源图像 (Source Image) 及源姿态 (Source Pose)中学到场景的先验知识 Scene Representation。这个 Scene Representation 可以是点云 (Point Cloud)，体素 (Voxel) 或者神经网络函数（Implicit Function）。

2）渲染：使用可微分渲染器（Differentiable Renderer），根据 Scene Representation 渲染得到预测的 2D image，且要和源图像 (Source Image) 尽可能地接近。

NeRF 框架图

发表在 ECCV 2020 的 NeRF 这篇论文在新视角合成任务上取得了很大的突破。以 NeRF 为例, 上面 的步骤可以具体化为:

• 1. 重建：用 MLP 网络学 Scene Representation。 输入源图像对应的三维空间坐标和视角 $(x,y,z,\theta ,\varphi );$ 输出 $(R,G,B,\sigma )$, 分别表示RGB 颜色值和体素密度。

• 2）渲染: 由 Volume Rendering 生成预测的 $2D$ image。 预测的 $2D$ image 和 ground truth image 之间算 L2 loss。

我会在后续的文章中介绍 Scene Representation 和 可微分渲染器（Differentiable Renderer）以 及一些新视角生成任务的典型方法。

2.Scene Representation

不同的Scene Representation

计算机图形学有很多不同的方式来建模物体，如图1所示，可以是基于平面的点云 (point cloud)、多边形网络 (polygonal mesh)，也可以是基于体素的占用（occupancy ），密度（density）等。每一种建模方式都对应一个函数解析式。如何求函数解析式的参数呢？在知道一些物体中采样点的坐标的情况下，我们可以用多项式泰勒展开、混合高斯模型等方法求解。

多层感知机（MLP）作为一个机器学习模型可以通用地拟合各种函数。用 MLP 这种神经网络模型来求解基于平面或体素的 scene representation 的函数解析式，就叫做 neural scene representation。MLP 的输入是空间的坐标，输出是这个坐标对应的属性。

以 NeRF 为例，NeRF 采用的是基于体素 (Voxel) 的表征方式，用 MLP 来拟合。MLP 的输入是源图像对应的三维空间坐标和视角$(x,y,z,\theta ,\varphi )$；输出是$(R,G,B,\sigma )$，分别表示RGB 颜色值和体素密度 。在得到了 $(R,G,B,\sigma )$ 这种表征之后，后面可以渲染出对应的图片。

位置编码（positional encoding）最早在 NLP 中采用，可以理解为给不同位置的坐标加一个不同的值作为先验。NeRF 及其后续的方法发现 MLP 的输入中加入位置编码能提高性能，更容易拟合高频域的函数。

2.1.NeRF 的 Scene Representation

3D Scene

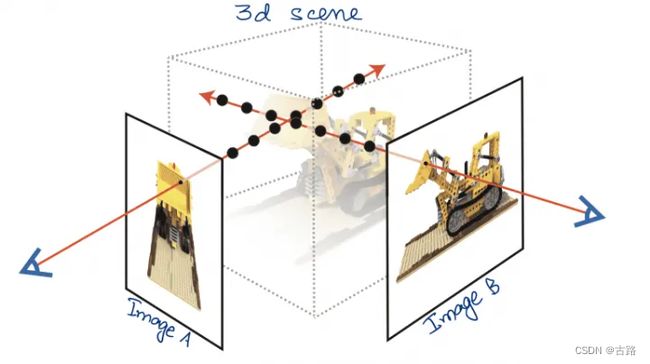
下面我们详细介绍 NeRF 的 scene representation。在上一节中已经提到，训练集包含来自不同视角的 2D 图片（例如图2中的黑色实线表示 Image A, Image B）以及对应的相机姿态矩阵。那么我们如何表示 3D scene 呢（即图2灰色虚线框表示的实体）？

这里涉及到光线追踪 (ray casting) 的基本知识。一条射线可以用公式 $r(t)=o+td$ 表示。其中符号 $o$ 表示原点的坐标， $d$ 是方向向量，$t$ 是参数。如下图3给出了 $t=3$ 时一条射线的可视化例子。

图3：光线追踪公式

我们可以从射线中随机采样一些点，例如图4中的 t1, t2, t3 三个点。图4 中蓝色的点表示均匀采样的位置，而 t1, t2, t3 的采样位置加入了噪声。

图4：射线采样

如图5所示，射线上每个点都可以由$(x,y,z,\theta ,\varphi )$ 表示，即三维空间坐标和视角。

图5：射线上的点可以用 $(x,y,z,\theta ,\varphi )$ 来表示

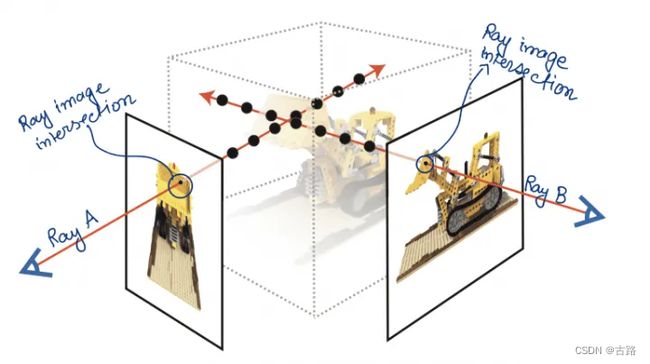
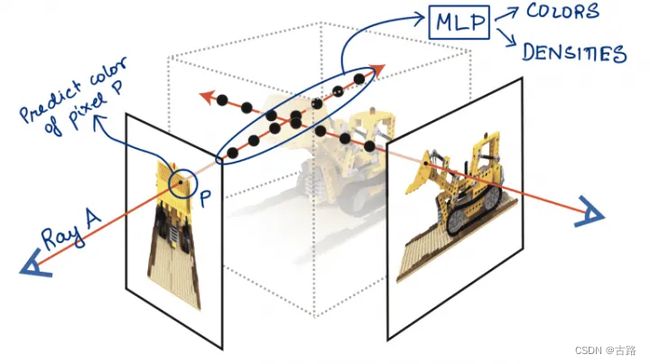
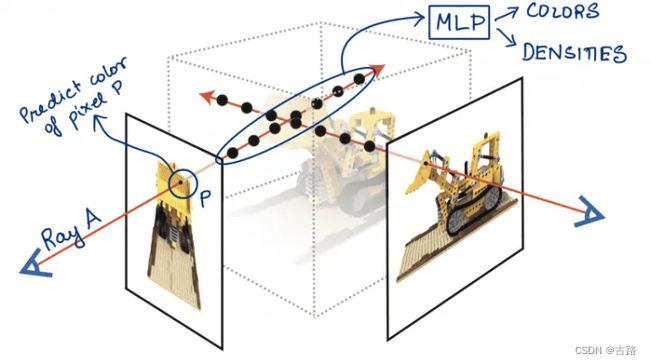
回到 NeRF，如图6所示，射线 A 上的每个像素都可以看作是射线和图片 A 的交点。射线 B 同理。

图6：射线 A, B 和图像的交点

根据之前图4的知识，我们可以在射线 A 上采样得到很多点 $(a_1,a_2,...)$ ，每个点都对应着 $(x,y,z,\theta ,\varphi )$ 的坐标。这些点就是 NeRF 的输入。

图7：在射线上采样点

NeRF 用 MLP 网络预测 $(a_1,a_2,...)$ 这些采样点的颜色和密度属性 $(R,G,B,\sigma )$，如图8所示。当我们知道了采样点的颜色和密度属性后，也可以反过来求图片 A 中像素 P 的 RGB 值，这一过程叫做 Volume rendering，会在下一篇文章中介绍。

图8：NeRF 的预测

此外，采样点的颜色和密度 $(a_1,a_2,...)$ 是没有 ground truth 的，怎么算损失函数呢？如图 9 所示，NeRF 通过 Volume rendering 这一步反过来求图片 A 中的每个像素的 RGB 值，得到了一个预测的渲染图像。渲染的图像通过 L2 loss 来保证和原图尽可能地接近。

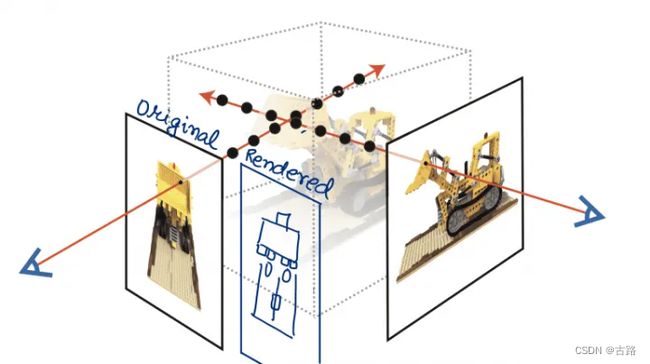
图9：NeRF 的重建函数

2.2.总结

本节介绍了3维视觉的一些几何表征方法，如点云，体素，以及射线的定义。 NeRF 用射线将三维空间中的采样点和二维图片中的像素点相结合， 来做3D scene representation 。

3.可微分渲染器 (Differentiable Renderer)

新视角合成关键有两步：Scene Representation 和 Differentiable Renderer。在第一步获得了 scene representation 之后，可微分渲染器 (Differentiable Renderer) 负责把 scene representation 转换成 2D 图像。根据 scene representation 的不同，渲染方法也可以分为平面渲染 (Surface Rendering) 和立体渲染 (Volumetric Rendering)。

3.1.立体渲染（volume rendering）

立体渲染 (volume rendering) 基于光线投射（ray casting），在新视角合成任务中被广泛使用。NeRF 就是用立体渲染的方法把 scene representation 转成 2D 图像。

图1 回顾了 上一节文章 中的内容。NeRF 用一条射线 $\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$ 连接了图片中的像素点 $P$ 和射线中的采样点。

图1：立体渲染

我们把希望求解的图片像素点 P 的RGB颜色值用符号 $C(\mathbf{r})$ 表示， $C(\mathbf{r})$ 可以看作是射线从近端的采样点 $t_n$到远端的采样点 $t_f$ 的积分：

$$C(\mathbf{r})={\int }_{t_n}^{t_f}T(t)\sigma (\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt$$

这个公式看起来很复杂，让我们拆解其中的每一项：

• $\mathbf{r}(t)$ : 射线的公式，$t$ 的取值范围是从近端 (near) 点 $t_n$ 到远端 (far) 点 $t_f$ ，也就是积分的上下限
• $\sigma (\mathbf{r}(t))$: 射线在点 $t$ 的体素密度 (density) 值，由 MLP 的预测结果得到
• $\mathbf{c}(\mathbf{r}(t),\mathbf{d})$ : 射线在点 $t$ 的 RGB 颜色 (color) 值，由 MLP 的预测结果得到；注意符号 $\mathbf{d}$ 是射线公式 $\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$ 里面的方向向量
• $T(t)$ 射线在点 $t$ 的透光率 (transmittance)，由体素密度 $\sigma (\mathbf{r}(t))$ 积分得到的，具体的公式是： $T(t)=\exp \left(-{\int }_{t_n}^t\sigma (\mathbf{r}(s))ds\right)$

总结一下，立体渲染就是求图片中像素点的 RGB 值 $C(\mathbf{r})$ 。 $C(\mathbf{r})$ 等于从近端到远端的采样点的透光率 (transmittance)，体素密度 (density) 和 RGB 颜色 (color) 的积分。这样我们就把 NeRF MLP 的预测结果利用了起来。

立体渲染的缺点：立体渲染需要沿着一条光线处理许多采样的点，每个采样点都需要送进神经网络前向传播一次得到对应的颜色和密度属性，因此渲染的速度比较慢。

3.2.总结

本文介绍了 NeRF 是怎样从 3D scene representation 重建出 2D 图像的。下一节会介绍更多 NeRF 的实现细节。

4.NeRF 实现细节

NeRF 是在静态（static）新视角合成任务上具有里程碑意义的方法。在前序的文章 (1) (2) (3) 中，我们已经介绍了 NeRF 的理论知识，包括数据格式，scene representation，volume rendering 以及损失函数。本文我们讨论更多 NeRF 的实现细节，包括 NeRF 的数据集，训练代码和测试代码。所有提到到的代码是源自 NeRF 官方开源的代码。

4.1.数据集

NeRF 的作者在 google drive 中开源了训练时用到的数据，包括生成的乐高数据 (nerf_synthetic) 和场景数据 (nerf_llff_data) 两个文件夹。以生成数据中的"hot dog"这一类为例，会包括

• “train / val / test” 三个包含图片的文件夹，以及
• “transforms_train.json”/“transforms_val.json”/“transforms_test.json” 三个包含每个图片的相机姿态的 json 文件

以 “transforms_train.json” 为例，其格式是这样的:

{
    "camera_angle_x": 0.6911112070083618,
    "frames": [
        {"file_path": "./train/r_0", "rotation": 0.012566370614359171,
         "transform_matrix": [[-0.9938939213752747,-0.10829982906579971,0.021122142672538757,0.08514608442783356],
                             [0.11034037917852402,-0.9755136370658875,0.19025827944278717,0.7669557332992554],
                             [0.0,0.19142703711986542,0.9815067052841187,3.956580400466919],
                             [0.0,0.0,0.0,1.0]]},
         ...
   ]
}

其中，camera_angle_x 是相机的水平视场 (horizontal field of view)，可以用于算焦距 (focal):

focal = 0.5 * image_width / np.tan(0.5 * camera_angle_x)

frames 是一个长度和 “train” 文件夹中图片数量相同的列表，这里只显示列表第一个元素的内容，包括对应的图片文件名 file_path ，和形状为 4x4 的 transform_matrix, 这个 transform_matrix 就是在第一节中介绍的用于从相机坐标到世界坐标转换的姿态矩阵（camera-to-world） C e x − 1 = [ r 11 ′ r 12 ′ r 13 ′ t x ′ r 21 ′ r 22 ′ r 23 ′ t y ′ r 31 ′ r 32 ′ r 33 ′ t z ′ 0 0 0 1 ] C_{e x}^{-1}=\left[\begin{array}{cccc} r_{11}^{\prime} & r_{12}^{\prime} & r_{13}^{\prime} & t_{x}^{\prime} \\ r_{21}^{\prime} & r_{22}^{\prime} & r_{23}^{\prime} & t_{y}^{\prime} \\ r_{31}^{\prime} & r_{32}^{\prime} & r_{33}^{\prime} & t_{z}^{\prime} \\ 0 & 0 & 0 & 1 \end{array}\right] Cex−1​= ​r11′​r21′​r31′​0​r12′​r22′​r32′​0​r13′​r23′​r33′​0​tx′​ty′​tz′​1​ ​ 。还有一个叫 rotation 的没有在代码中用到，可以忽略。

NeRF 的代码中，由一个叫 load_blender_data 的函数根据上述的 json 文件读入 image，transform_matrix 等信息。

4.2.训练代码

在第二节中，我们已经介绍了 NeRF 是如何用射线来建模整个 3D 场景的，下面我们来看看具体的代码实现，主要包括两部分：生成射线和渲染。

首先我们介绍如何生成射线。回顾第一二节，一条射线可以用公式 $r(t)=o+td$ 来表示。首先我们通过下面的 get_rays 函数得到射线的原点 $o$ 和方向单位向量 $d$。

def get_rays(H, W, focal, c2w):
    """Get ray origins, directions from a pinhole camera."""
    i, j = tf.meshgrid(tf.range(W, dtype=tf.float32),
                       tf.range(H, dtype=tf.float32), indexing='xy')
    dirs = tf.stack([(i-W*.5)/focal, -(j-H*.5)/focal, -tf.ones_like(i)], -1)
    rays_d = tf.reduce_sum(dirs[..., np.newaxis, :] * c2w[:3, :3], -1)
    rays_o = tf.broadcast_to(c2w[:3, -1], tf.shape(rays_d))
    return rays_o, rays_d

这个函数的

• 输入是图片的高度 H，宽度 W，相机的焦距 focal （由上述 json 文件的 camera_angle_x 得到）和相机的姿态矩阵 c2w（由上述 json 文件的 transform_matrix 得到）。这个函数的
• 输出就是射线的原点 o 和方向单位向量 d ，也就是 rays_o, rays_d 这两个变量。在 NeRF 中，一张图片的每个像素都对应一条指向相机光圈的射线。

因此我们首先计算图片中每个像素在图片坐标系中的坐标，和图片高度/宽度有关:

# 创建一个meshgrid ，含义就是图片中的每个像素的坐标
i, j = tf.meshgrid(tf.range(W, dtype=tf.float32),
                   tf.range(H, dtype=tf.float32), indexing='xy')

i, j 都是形状为 (H, W) 的数组，比如说 (i[0], j[0]) 就可以表示图片坐标系中 (0, 0) 这一点的坐标。

假设图片坐标系中有一点 (u, v) ，如何找到其对应的相机坐标系中的坐标 (x_{c}, y_{c}, z_{c}) 呢？根据针孔相机的成像原理（如下图1所示），存在下面的转换关系：

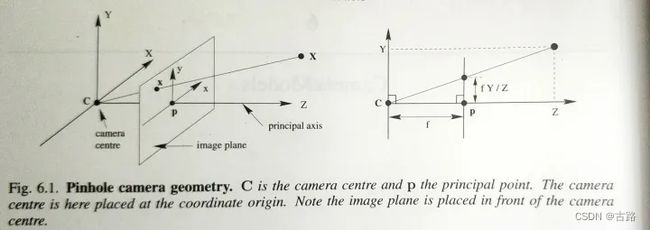
图1：对于针孔相机模型，从图片坐标系到相机坐标系的坐标转换

$$x_c=z_c\frac{u-o_x}{f}$$$$y_c=z_c\frac{v-o_y}{f}$$

其中 $o_x,o_y$ 指的是图片的中心点 $(H/2,W/2)$。根据这个公式，从图片坐标系到相机坐标系就是下面的代码，tf.ones_like(i) 是为了齐次坐标：

# 从图片坐标系转换到相机坐标系
dirs = tf.stack([(i-W*.5)/focal, -(j-H*.5)/focal, -tf.ones_like(i)], -1)

下面从相机坐标系转换到射线所在的世界坐标系。在从相机坐标到世界坐标转换的姿态矩阵矩阵 C e x − 1 = [ r 11 ′ r 12 ′ r 13 ′ t x ′ r 21 ′ r 22 ′ r 23 ′ t y ′ r 31 ′ r 32 ′ r 33 ′ t z ′ 0 0 0 1 ] C_{e x}^{-1}=\left[\begin{array}{cccc} r_{11}^{\prime} & r_{12}^{\prime} & r_{13}^{\prime} & t_{x}^{\prime} \\ r_{21}^{\prime} & r_{22}^{\prime} & r_{23}^{\prime} & t_{y}^{\prime} \\ r_{31}^{\prime} & r_{32}^{\prime} & r_{33}^{\prime} & t_{z}^{\prime} \\ 0 & 0 & 0 & 1 \end{array}\right] Cex−1​= ​r11′​r21′​r31′​0​r12′​r22′​r32′​0​r13′​r23′​r33′​0​tx′​ty′​tz′​1​ ​ 中，上三角的 [ r 11 ′ r 12 ′ r 13 ′ r 21 ′ r 22 ′ r 23 ′ r 31 ′ r 32 ′ r 33 ′ ] \left[\begin{array}{cccc} r_{11}^{\prime} & r_{12}^{\prime} & r_{13}^{\prime} & \\ r_{21}^{\prime} & r_{22}^{\prime} & r_{23}^{\prime} & \\ r_{31}^{\prime} & r_{32}^{\prime} & r_{33}^{\prime} & \\ \end{array}\right] ​r11′​r21′​r31′​​r12′​r22′​r32′​​r13′​r23′​r33′​​​ ​ 定义了相机的旋转，可以得到射线的方向向量 $d$ 。而 [ t x ′ t y ′ t z ′ ] \left[\begin{array}{ccc} t_{x}^{\prime} \\ t_{y}^{\prime} \\ t_{z}^{\prime} \\ \end{array}\right] ​tx′​ty′​tz′​​ ​ 定义了相机的平移，可以得到射线的原点 $o$ ，也就是对应了 get_rays 函数代码的最后两行:

# 射线的方向向量，c2w[:3, :3] 对应 [r11', ... ,r33']
rays_d = tf.reduce_sum(dirs[..., np.newaxis, :] * c2w[:3, :3], -1)
# 射线的原点，c2w[:3, -1] 对应 [tx', ty', tz']
rays_o = tf.broadcast_to(c2w[:3, -1], tf.shape(rays_d))

介绍完了函数 get_rays 之后，回到射线的公式 $r(t)=o+td$ 下面我们介绍如何从射线中出采样点。回顾第二节，我们在近端点 $t_n$ 和远端点 $t_f$ 之间随机均匀采样 N 个点，其对应的公式如下：

$$t_i\sim \mathcal{U}\left[t_n+\frac{i-1}{N}\left(t_f-t_n\right),t_n+\frac{i}{N}\left(t_f-t_n\right)\right]$$

代码如下，变量 pts 就是从射线中采样得到的点：

 # Compute 3D query points
 z_vals = tf.linspace(near, far, N_samples) 
 if rand:
   z_vals += tf.random.uniform(list(rays_o.shape[:-1]) + [N_samples]) 
   				* (far-near)/N_samples
 pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None]

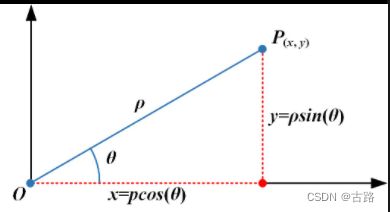
随后我们把 pts 由极坐标转换到平面坐标系，也就是图2中高中数学里的三角函数内容：

def posenc(x):
  rets = [x]
  for i in range(L_embed):
    for fn in [tf.sin, tf.cos]:
      rets.append(fn(2.**i * x))
  return tf.concat(rets, -1)

pts_flat = tf.reshape(pts, [-1,3])
pts_flat = posenc(pts_flat)

图2：极坐标到平面坐标转换
随后把射线上的点送进 MLP 网络，得到预测的值：

raw = model(pts_flat)
raw = tf.reshape(raw, list(pts.shape[:-1]) + [4])
sigma_a = tf.nn.relu(raw[...,3])
rgb = tf.math.sigmoid(raw[...,:3]) 

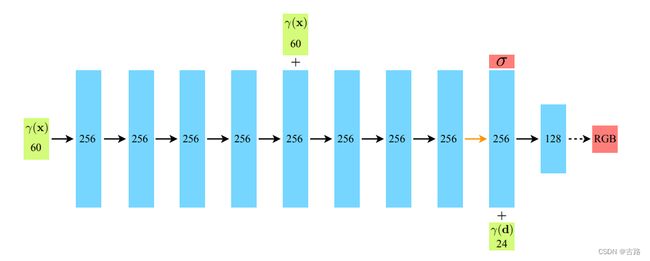
这里变量 model 就是下图3中的 NeRF 的 MLP 的结构。图中 \gamma(\mathbf{x}) 指的就是射线上采样的点， $\gamma (\mathbf{d})$ 指的是位置编码（positional encoding）。网络的输出是颜色 RGB 以及 密度 $\sigma$ 。

图3：MLP 的结构

下面我们介绍最后一个部分，也就是第三节中提到的立体渲染的代码，其对应的公式为：

$$\hat{C}(\mathbf{r})=\sum _{i=1}^N{T}_i\left(1-\exp \left(-{\sigma }_i{\delta }_i\right)\right){\mathbf{c}}_i,\text{ where }{T}_i=\exp \left(-\sum _{j=1}^{i-1}{\sigma }_j{\delta }_j\right)$$

和第三节中的公式稍微有点区别，因为是要在计算机上实现积分的过程，所以要离散化。对应的代码如下：

dists = tf.concat([z_vals[..., 1:] - z_vals[..., :-1], 
			tf.broadcast_to([1e10], z_vals[...,:1].shape)], -1) 
alpha = 1.-tf.exp(-sigma_a * dists)
weights = alpha * tf.math.cumprod(1.-alpha + 1e-10, -1, exclusive=True)
    
rgb_map = tf.reduce_sum(weights[...,None] * rgb, -2) 
depth_map = tf.reduce_sum(weights * z_vals, -1) 
acc_map = tf.reduce_sum(weights, -1) 

变量 dists 指的是射线上采样点之间的 delta 值 ${\delta }_i=t_{i+1}-t_i$ ，给积分用。变量 alpha 指的是 ${\alpha }_i=1-\exp \left(-{\sigma }_i{\delta }_i\right)$ ，计算透光率 $T_i$ 用的。变量 weights 就是 $T_i\left(1-\exp \left(-{\sigma }_i{\delta }_i\right)\right)$ 积分的值，变量 rgb_map 就是积分后得到的 $\hat{C}(\mathbf{r})$ ，也就是立体渲染的输出，预测的像素 pixel 值。

前面已经介绍了如何生成射线，以及如何做立体渲染。把两者结合，NeRF 训练的代码非常的简洁，主干就三行，相信你已经很容易看懂了：

# 生成射线
rays_o, rays_d = get_rays(H, W, focal, pose)
# 立体渲染
rgb, depth, acc = render_rays(model, rays_o, rays_d, near=2., far=6., N_samples=64)
# 计算 mse loss
loss = tf.reduce_mean(tf.square(rgb - gt_img))

这三行代码也就对应了 NeRF 的框架图，如图4所示：

图4：NeRF 框架图: (a)，(b)表示生成射线，©表示立体渲染，(d)表示算 mse loss。

4.3.测试阶段

成功训练好了 NeRF 之后，我们用 MLP 对整个 3D 场景进行了建模。测试的时候，我们可以绕着 $\theta$ 轴旋转相机，得到 360度的新视角的合成结果（训练集没有的视角），其代码如下：

frames = []
# 绕着 theta 轴 360 度旋转
for th in tqdm(np.linspace(0., 360., 120, endpoint=False)):
    # 得到当前 theta 值对应的姿态矩阵
    c2w = pose_spherical(th, -30., 4.)
    # 生成射线
    rays_o, rays_d = get_rays(H, W, focal, c2w[:3,:4])
    # 渲染
    rgb, depth, acc = render_rays(model, rays_o, rays_d, near=2., far=6., N_samples=N_samples)
    # 保存当前帧的结果
    frames.append((255*np.clip(rgb,0,1)).astype(np.uint8))

# 把所有帧的结果输出成 video
import imageio
f = 'video.mp4'
imageio.mimwrite(f, frames, fps=30, quality=7)

根据当前的 $\theta$ 得到姿态矩阵的函数 pose_spherical 代码如下所示：

trans_t = lambda t : tf.convert_to_tensor([
    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,t],
    [0,0,0,1],
], dtype=tf.float32)

rot_phi = lambda phi : tf.convert_to_tensor([
    [1,0,0,0],
    [0,tf.cos(phi),-tf.sin(phi),0],
    [0,tf.sin(phi), tf.cos(phi),0],
    [0,0,0,1],
], dtype=tf.float32)

rot_theta = lambda th : tf.convert_to_tensor([
    [tf.cos(th),0,-tf.sin(th),0],
    [0,1,0,0],
    [tf.sin(th),0, tf.cos(th),0],
    [0,0,0,1],
], dtype=tf.float32)


def pose_spherical(theta, phi, radius):
    c2w = trans_t(radius)
    c2w = rot_phi(phi/180.*np.pi) @ c2w
    c2w = rot_theta(theta/180.*np.pi) @ c2w
    c2w = np.array([[-1,0,0,0],[0,0,1,0],[0,1,0,0],[0,0,0,1]]) @ c2w
    return c2w

4.4.总结

本节介绍了 NeRF 的数据集格式以及训练和测试的代码细节。NeRF 只是建模静态的场景，在后面的文章中，我们会介绍一些基于 NeRF 建模动态场景（例如视频）的改进工作。

兄弟，看了你写的，有些地方不对。这个i,j的形状是(W,H)吧。所以中心点坐标也肯定不对，dirs的推算也不是这样的。 后面这个posenc是位置编码吧，不是将极坐标转换为直角坐标。有个小问题,posenc应该是positional encoding而不是极坐标转换吧?

5.动态场景的表征和渲染

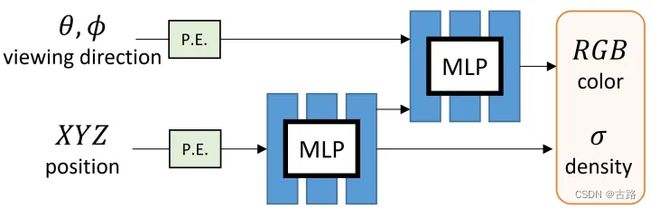
在前面几节 中，我们介绍了对于静态场景的新视角合成方法，对于相同的物体，输入的图片来自同一时刻不同的角度。例如图1表示的是 NeRF 的框架图，输入是静态的空间坐标 $(x, y, z, \theta, \phi) $，输出是 $(C,\sigma )$ ，表示RGB 颜色值 $C$ 和 密度 $\sigma$ 。

图1：NeRF 框架图。作用于静态场景：输入坐标+视角(x, y, z, theta, phi)，输出颜色 RGB 和密度 sigma

那么如果输入是来自不同时刻呢？当输入从二维的静态图片扩张到三维的动态视频，如何把时间的信息加入进来呢？

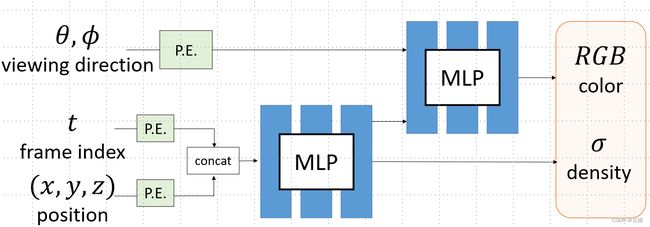
一个直观的想法就是把时间 $T$ 也加到输入中，相当于输入除了由 $(x,y,z,\theta ,\varphi )$ 这些空间坐标，还额外加入了一个表示时间坐标轴 $T$ 。对应论文 $NSFF[1]，Video-NeRF[2]，NeRFlow[3]$，如图2所示。下面我们以 NSFF 为例来介绍。

图2：从静态到动态：把帧的时间坐标 t 也加入到输入中

5.1.NSFF (Neural Scene Flow Fields), CVPR 2021

相比NeRF，NSFF 的输入是 $(x,y,z,\theta ,\varphi ,t)$ ，多了一个时间坐标 $t$ ；输出是 $(C,\sigma ,\mathcal{F},\mathcal{W})$ ，多了 3D 场景流 (3D scene flow) $\mathcal{F}$ 和 运动遮挡权重(disocclusion weight) $\mathcal{W}$ 。

对于第 $i$ 帧，其3D场景流的定义为 ${\mathcal{F}}_i=\left({\mathbf{f}}_{i\to i+1},{\mathbf{f}}_{i\to i-1}\right)$ ，表示从第 $t$ 帧到第 $i+1$ 帧和从第 $t$ 帧到第 $t-1$ 帧的位置偏置向量 (offset vectors)。回顾第二节，我们用符号 $r_i$ 表示第 $i$ 帧的一条射线，那么加上从第 $i$ 帧到第 $i+1$ 帧的位置偏置向量就可以表示第 $i+1$ 帧的射线，如下面的公式所示：

$${\mathbf{r}}_{i\to i+1}={\mathbf{r}}_i+{\mathbf{f}}_{i\to i+1}$$

为什么要考虑每一帧前后的信息呢？这是为了视频帧之间的时序一致性(Temporal consistency)。假设我们用符号 $j$ 表示第 $i$ 帧的相邻帧，即 $j\in \mathcal{N}(i)$ 。作者在实现中取的是相邻两帧 $\mathcal{N}(i)=\{i,i\pm 1,i\pm 2\}$ 。NSFF 算法的立体渲染过程可以理解为输入第 $j$ 帧的位置坐标，以及从第 $i$ 帧到第 $j$ 帧之间的位置偏置向量，预测第 $i$ 帧的颜色值 ${\hat{\mathbf{C}}}_{j\to i}$ ，如下面的积分公式：

$${\hat{\mathbf{C}}}_{j\to i}\left({\mathbf{r}}_i\right)={\int }_{t_n}^{t_f}{T}_j(t){\sigma }_j\left({\mathbf{r}}_{i\to j}(t)\right){\mathbf{c}}_j\left({\mathbf{r}}_{i\to j}(t),{\mathbf{d}}_i\right)dt$$

注意这里积分的 $t$ 表示的是射线的参数。和第三节中 NeRF 在静态场景下的公式对比，可以看出其实就是多了 ${\mathcal{F}}_i$ 定义的 $i$ 和 $j$ 之间的偏置转换。

预测的颜色值 ${\hat{\mathbf{C}}}_{j\to i}$ 和第 $i$ 帧的标注 ${\mathbf{C}}_i\left({\mathbf{r}}_i\right)$ 之间可以算用于重建的损失函数 ${\mathcal{L}}_{\text{pho }}$ ：

L pho  = ∑ r i ∑ j ∈ N ( i ) ∥ C ^ j → i ( r i ) − C i ( r i ) ∥ 2 2 \mathcal{L}_{\text {pho }}=\sum_{\mathbf{r}_{i}} \sum_{j \in \mathcal{N}(i)}\left\|\hat{\mathbf{C}}_{j \rightarrow i}\left(\mathbf{r}_{i}\right)-\mathbf{C}_{i}\left(\mathbf{r}_{i}\right)\right\|_{2}^{2} Lpho ​=ri​∑​j∈N(i)∑​ ​C^j→i​(ri​)−Ci​(ri​) ​22​

但是只用3D场景流可能会带来帧之间遮挡&歧义的问题，因此作者又加入了运动遮挡权重，定义也包括从第 $t$ 帧向前/向后一帧的结果${\mathcal{W}}_i=\left(w_{i\to i+1},w_{i\to i-1}\right)$ 。而 $w$ 的取值是0或者1，可以看作是一个无监督的置信度。这样立体渲染的公式和用于重建的损失函数 ${\mathcal{L}}_{\text{pho }}$就变成了：

$${\hat{W}}_{j\to i}\left({\mathbf{r}}_i\right)={\int }_{t_n}^{t_f}{T}_j(t){\sigma }_j\left({\mathbf{r}}_{i\to j}(t)\right)w_{i\to j}\left({\mathbf{r}}_i(t)\right)dt$$

L pho  = ∑ r i ∑ j ∈ N ( i ) W ^ j → i ( r i ) ∥ C ^ j → i ( r i ) − C i ( r i ) ∥ 2 2 + β w ∑ x i ∥ w i → j ( x i ) − 1 ∥ ∥ 1 \begin{array}{r} \mathcal{L}_{\text {pho }}=\sum_{\mathbf{r}_{i}} \sum_{j \in \mathcal{N}(i)} \hat{W}_{j \rightarrow i}\left(\mathbf{r}_{i}\right)\left\|\hat{\mathbf{C}}_{j \rightarrow i}\left(\mathbf{r}_{i}\right)-\mathbf{C}_{i}\left(\mathbf{r}_{i}\right)\right\|_{2}^{2} +\beta_{w} \sum_{\mathbf{x}_{i}}\left\|w_{i \rightarrow j}\left(\mathbf{x}_{i}\right)-1\right\| \|_{1} \end{array} Lpho ​=∑ri​​∑j∈N(i)​W^j→i​(ri​) ​C^j→i​(ri​)−Ci​(ri​) ​22​+βw​∑xi​​∥wi→j​(xi​)−1∥∥1​​

后面的正则项 ${\sum }_{{\mathbf{x}}_i}\Vert w_{i\to j}\left({\mathbf{x}}_i\right)-1\Vert {\Vert }_1$ 是为了鼓励 $w_{i\to j}$ 的值取1。

5.2.辅助训练的损失函数

此外，之前的方法~[1, 2, 3] 还针对视频任务的特性，加入各种辅助训练的损失函数，例如：

一致性：NFSS 加入cycle-consistency loss ${\mathcal{L}}_{\mathrm{cyc}}$让从 $i\to j$ 和 $j\to i$ 之间的3D场景流保持一致性。NeRFlow~[3] 添加了三个额外的损失函数来保证外观 (Appearance)，密度 (Density) 和运动 (Motion) 之间的一致性。
深度信息：Video-NeRF~[2] 从射线的透光率中积分得到深度信息 $\hat{D}(\mathbf{r},t)={\int }_{s_{\mathrm{n}}}^{s_{\mathrm{f}}}T(s,t)\sigma (\mathbf{r}(s),t)s\mathrm{d}s$ ，并加入重建深度信息的损失函数 $\hat{D}(\mathbf{r},t)={\int }_{s_{\mathrm{n}}}^{s_{\mathrm{f}}}T(s,t)\sigma (\mathbf{r}(s),t)s\mathrm{d}s$

5.3.总结

本节介绍了新视角生成任务从二维的静态图片扩张到三维的动态视频的一些基于 NeRF 改进的方法。可以看出比静态场景要复杂很多，基本上每篇工作都要加上各种损失函数来保证建模出 3D 场景。

此外对于动态场景，我们还要考虑物体运动中的形变 (deformation) 的问题，会在下一篇文章中介绍。

6.基于形变模型的动态场景重建

关于动态场景的视角合成，上一节介绍了一类把时间帧加入到 NeRF 输入的方法，可以称作是动态 NeRF。本文介绍另外一类方法，如下图1所示，由静态的 NeRF 加上一个额外的形变模型 (deformation model) 组成。这一类方法的代表工作有 D-NeRF (CVPR 2021), Nerfies (ICCV 2021) 和 NR-NeRF (ICCV 2021)。

图1：基于静态 NeRF + 形变模型重建动态场景

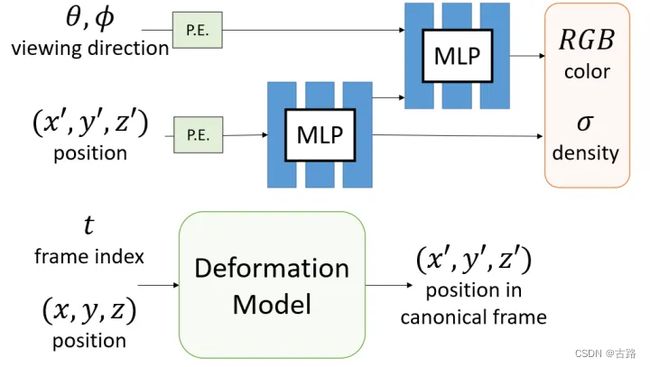
这三篇文章是同期的工作，细节上很相似，我们选取 D-NeRF~[1] 为例子来介绍，其对应的流程图如图2所示：

图2：D-NeRF 流程图

整个流程是这样的：作者先定义了 $t=0$ 时的场景为起点（canonical space）。给定输入位置坐 标 $(x,y,z)$, 作者先用一个 deformation model ${\Psi }_t$ 预测从起点到输入指定时间之间的位置偏置 $(\Delta x,\Delta y,\Delta z)$ 。
这个形变模型 ${\Psi }_t$ 也是一个简单的 MLP 网络, 就是预测偏置值, 公式如下所示:
$${\Psi }_t(\mathbf{x},t)=\{\begin{array}{ll}\Delta \mathbf{x},& \text{ if }t\ne 0\\ 0,& \text{ if }t=0\end{array}$$
然后把新的位置坐标 $(x+\Delta x,y+\Delta y,z+\Delta z,\theta ,\varphi )$ 送入 NeRF, 得到重建的颜色和密度结 果 $(R,G,B,\sigma )$ 就可以和 NeRF 一样算重建的损失函数。
引用

• [1] D-NeRF: Neural Radiance Fields for Dynamic Scenes, CVPR 2021
• [2] Nerfies: Deformable Neural Radiance Fields, ICCV 2021
• [3] Non-Rigid Neural Radiance Fields: Reconstruction and Novel View Synthesis of a Dynamic Scene From Monocular Video, ICCV 2021