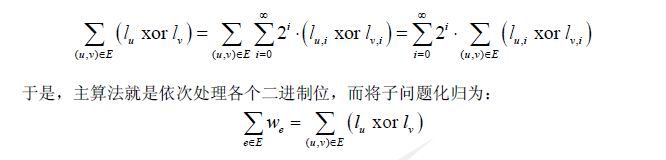spoj839 Optimal Marks 最小割模型
考虑到是异或运算求最小cost之和,由于对于二进制,各个位之间是互不影响的,所以可以将问题转会为每个二进制位的求解,然后求和即可。对于每个二进制位,要么为0,要么为1, 就想到将整个图切割成两个点集,即对于每个点,都只有两种取值,可以看成是要将点集划分成两类。在这种分类思想的指导下,重新考察操作的意义:对于边的两个端点,若它们同类则边权无值;若它们异类则边权有值1。
建图方式:
建一源点S,汇点T
对于已经标号过的点:
1. 对于位为1的点建边<S, V, INF, 0>
2. 对于位为0的点建边<V, T, INF, 0>
对于所有的原边
建成流量为1的双向边<u, v, 1, 1>
这样求得最小割,即为当前位的最优解。
这样建边,求最小割时,保证了割边都是原边,求完后,所有与S相连的点可以标号为1, 所有与T相连的边标号为0, 那么这些割边即为相邻点异类的边,同时保证了他们的和最小。
刚开始一直没明白一句话,如果有多组解,输出顶点标号和最小的解,从上面的求解过程可以看出,如果只求到最大标号的最高位,那么解顶点标号和事唯一的,也就是说,只要求到最大标号的最高位即可。
1 #include < stdio.h >
2 #include < string .h >
3 #define INF 0x3fffffff
4 #define NN 504
5 #define MM 8010
6
7 typedef struct node{
8 int v, w;
9 struct node * nxt, * op;
10 }NODE;
11 NODE edg[MM];
12 NODE * Link[NN];
13 int h[NN];
14 int num[NN]; // gap优化,标号为i的顶点个数
15 int cnt[NN];
16 int vis[NN];
17 int mark[NN];
18 int x[ 3004 ], y[ 3004 ];
19
20 int M, N, idx, S, T, n; // S 表示源点,T表示汇点,n表示节点个数
21
22 void Add( int u, int v, int c1, int c2){
23 idx ++ ; // idx记得初始化,不然很容易栈溢出
24 edg[idx].v = v;
25 edg[idx].w = c1;
26 edg[idx].nxt = Link[u];
27 edg[idx].op = edg + idx + 1 ;
28 Link[u] = edg + idx;
29 idx ++ ;
30 edg[idx].v = u;
31 edg[idx].w = c2; // 有向边为0,无向边为c
32 edg[idx].nxt = Link[v];
33 edg[idx].op = edg + idx - 1 ;
34 Link[v] = edg + idx;
35 }
36
37 int Min( int a, int b){
38 return a < b ? a : b;
39 }
40
41 int aug( int u, int flow){
42 if (u == T) return flow;
43 int l = flow; // l表示剩余容量
44 int tmp = n - 1 ;
45 for (NODE * p = Link[u]; p; p = p -> nxt){
46 if (h[u] == h[p -> v] + 1 && p -> w){
47 int f = aug(p -> v, Min(l, p -> w));
48 l -= f;
49 p -> w -= f;
50 p -> op -> w += f;
51 if (l == 0 || h[S] == n) return flow - l; // gap
52 }
53 if (p -> w > 0 && h[p -> v] < tmp){
54 tmp = h[p -> v];
55 }
56 }
57 if (l == flow){
58 num[h[u]] -- ; // gap
59 if (num[h[u]] == 0 ) h[S] = n; // gap,每个点的距离值最多为n - 1,这里设为n 表示断层了
60 else {
61 h[u] = tmp + 1 ;
62 num[h[u]] ++ ; // gap
63 }
64 }
65 return flow - l;
66 }
67
68 void Init(){
69 idx = 0 ;
70 S = 0 ;
71 T = N + 1 ;
72 n = T + 1 ;
73 memset(Link, 0 , sizeof (Link));
74 }
75 /* n表示总点的个数,包括源点和汇点 */
76 int sap(){
77 int ans = 0 ;
78 memset(h, 0 , sizeof (h));
79 memset(num, 0 , sizeof (num));
80 num[ 0 ] = n;
81 while (h[S] < n){
82 ans += aug(S, INF);
83 }
84 return ans;
85 }
86
87
88 void dfs( int u, int base ){ // 所有能搜到的点,都是当前位为1的点
89 cnt[u] += base ;
90 for (NODE * p = Link[u]; p; p = p -> nxt){
91 if (p -> w && ! vis[p -> v]){
92 vis[p -> v] = 1 ;
93 dfs(p -> v, base );
94 }
95 }
96 }
97 void Solve(){
98 int flag, base , i;
99 flag = 1 ;
100 base = 1 ;
101 memset(cnt, 0 , sizeof (cnt)); // 记录每个点的最后标号
102 while (flag){ // 对每一位作处理,一直到最高位为0为止
103 flag = 0 ;
104 Init();
105 for (i = 1 ; i <= M; i ++ ){
106 Add(x[i], y[i], 1 , 1 );
107 }
108
109 for (i = 1 ; i <= N; i ++ ){
110 if (mark[i] != - 1 ){
111 if (mark[i] >= 1 ){
112 flag = 1 ;
113 }
114 if (mark[i] % 2 ){
115 Add(S, i, INF, 0 );
116 } else {
117 Add(i, T, INF, 0 );
118 }
119 mark[i] /= 2 ;
120 }
121 }
122 sap();
123 memset(vis, 0 , sizeof (vis));
124 vis[S] = 1 ;
125 dfs(S, base );
126 base *= 2 ;
127 }
128 for (i = 1 ; i <= N; i ++ ){
129 printf( " %d\n " , cnt[i]);
130 }
131 }
132 int main()
133 {
134 int iT, i, K, u, p;
135 scanf( " %d " , & iT);
136 while (iT -- ){
137 scanf( " %d%d " , & N, & M);
138 for (i = 1 ; i <= M; i ++ ){
139 scanf( " %d%d " , & x[i], & y[i]);
140 }
141 scanf( " %d " , & K);
142 memset(mark, - 1 , sizeof (mark));
143 for (i = 1 ; i <= K; i ++ ){
144 scanf( " %d%d " , & u, & p);
145 mark[u] = p;
146 }
147 Solve();
148 }
149 return 0 ;
150 }
151