第八届蓝桥杯Java B组题解
A.购物单
题目描述
小明刚刚找到工作,老板人很好,只是老板夫人很爱购物。老板忙的时候经常让小明帮忙到商场代为购物。小明很厌烦,但又不好推辞。
这不,XX大促销又来了!老板夫人开出了长长的购物单,都是有打折优惠的。
小明也有个怪癖,不到万不得已,从不刷卡,直接现金搞定。
现在小明很心烦,请你帮他计算一下,需要从取款机上取多少现金,才能搞定这次购物。
取款机只能提供100元面额的纸币。小明想尽可能少取些现金,够用就行了。
你的任务是计算出,小明最少需要取多少现金。
以下是让人头疼的购物单,为了保护隐私,物品名称被隐藏了。
**** 180.90 88折
**** 10.25 65折
**** 56.14 9折
**** 104.65 9折
**** 100.30 88折
**** 297.15 半价
**** 26.75 65折
**** 130.62 半价
**** 240.28 58折
**** 270.62 8折
**** 115.87 88折
**** 247.34 95折
**** 73.21 9折
**** 101.00 半价
**** 79.54 半价
**** 278.44 7折
**** 199.26 半价
**** 12.97 9折
**** 166.30 78折
**** 125.50 58折
**** 84.98 9折
**** 113.35 68折
**** 166.57 半价
**** 42.56 9折
**** 81.90 95折
**** 131.78 8折
**** 255.89 78折
**** 109.17 9折
**** 146.69 68折
**** 139.33 65折
**** 141.16 78折
**** 154.74 8折
**** 59.42 8折
**** 85.44 68折
**** 293.70 88折
**** 261.79 65折
**** 11.30 88折
**** 268.27 58折
**** 128.29 88折
**** 251.03 8折
**** 208.39 75折
**** 128.88 75折
**** 62.06 9折
**** 225.87 75折
**** 12.89 75折
**** 34.28 75折
**** 62.16 58折
**** 129.12 半价
**** 218.37 半价
**** 289.69 8折
需要说明的是,88折指的是按标价的88%计算,而8折是按80%计算,余者类推。
特别地,半价是按50%计算。
请提交小明要从取款机上提取的金额,单位是元。
答案是一个整数,类似4300的样子,结尾必然是00,不要填写任何多余的内容。
题目分析
只要将数据用文本工具修改一下,***转化为"+",数字之间的空格转换为""即可。
题解
答案 5200
public class Main {
public static void main(String[] args) {
double sum = 0 + 180.90 * 88
+ 10.25 * 65
+ 56.14 * 90
+ 104.65 * 90
+ 100.30 * 88
+ 297.15 * 50
+ 26.75 * 65
+ 130.62 * 50
+ 240.28 * 58
+ 270.62 * 80
+ 115.87 * 88
+ 247.34 * 95
+ 73.21 * 90
+ 101.00 * 50
+ 79.54 * 50
+ 278.44 * 70
+ 199.26 * 50
+ 12.97 * 90
+ 166.30 * 78
+ 125.50 * 58
+ 84.98 * 90
+ 113.35 * 68
+ 166.57 * 50
+ 42.56 * 90
+ 81.90 * 95
+ 131.78 * 80
+ 255.89 * 78
+ 109.17 * 90
+ 146.69 * 68
+ 139.33 * 65
+ 141.16 * 78
+ 154.74 * 80
+ 59.42 * 80
+ 85.44 * 68
+ 293.70 * 88
+ 261.79 * 65
+ 11.30 * 88
+ 268.27 * 58
+ 128.29 * 88
+ 251.03 * 80
+ 208.39 * 75
+ 128.88 * 75
+ 62.06 * 90
+ 225.87 * 75
+ 12.89 * 75
+ 34.28 * 75
+ 62.16 * 58
+ 129.12 * 50
+ 218.37 * 50
+ 289.69 * 80;
sum = Math.ceil(sum / 100 / 100) * 100;
System.out.println(sum);
}
}
B.纸牌三角形
题目描述
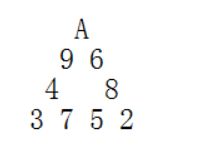
A,2,3,4,5,6,7,8,9 共9张纸牌排成一个正三角形(A按1计算)。要求每个边的和相等。
下图就是一种排法
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
注意:需要提交的是一个整数,不要提交任何多余内容。
题目分析
归根结底这是一道全排列的问题,可以用深搜来解决。考虑到旋转以及镜像的影响,最后结果要除以6。
题解
144
public class Main {
static int[] map = new int[10];
static boolean[] vis = new boolean[10];
static int ans;
static void dfs(int step, int n) {
if (step == 10) {
int n1 = map[1] + map[2] + map[3] + map[4];
int n2 = map[4] + map[5] + map[6] + map[7];
int n3 = map[7] + map[8] + map[9] + map[1];
if (n1 == n2 && n2 == n3) ans++;
return;
} else {
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
map[step] = i;
vis[i] = true;
dfs(step + 1, n);
vis[i] = false;
}
}
}
}
public static void main(String[] args) {
dfs(1, 9);
System.out.println(ans / 6);
}
}
C.承压计算
题目描述
X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。
每块金属原料的外形、尺寸完全一致,但重量不同。
金属材料被严格地堆放成金字塔形。
7
5 8
7 8 8
9 2 7 2
8 1 4 9 1
8 1 8 8 4 1
7 9 6 1 4 5 4
5 6 5 5 6 9 5 6
5 5 4 7 9 3 5 5 1
7 5 7 9 7 4 7 3 3 1
4 6 4 5 5 8 8 3 2 4 3
1 1 3 3 1 6 6 5 5 4 4 2
9 9 9 2 1 9 1 9 2 9 5 7 9
4 3 3 7 7 9 3 6 1 3 8 8 3 7
3 6 8 1 5 3 9 5 8 3 8 1 8 3 3
8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9
8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4
2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9
7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6
9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3
5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9
6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4
2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4
7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6
1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3
2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8
7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9
7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6
5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1
X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X
其中的数字代表金属块的重量(计量单位较大)。
最下一层的X代表30台极高精度的电子秤。
假设每块原料的重量都十分精确地平均落在下方的两个金属块上,
最后,所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小,所以显示的数字很大。
工作人员发现,其中读数最小的电子秤的示数为:2086458231
请你推算出:读数最大的电子秤的示数为多少?
注意:需要提交的是一个整数,不要填写任何多余的内容。
题目分析
如果我们单纯地将输入的数据除以2分别加到下方的两个数上面,一个很大的问题就是再最后计算的时候需要考虑到小数和精确度的问题,这会严重影响我们的计算结果。因为这个金字塔有30层,可以对没一个输入的数据乘以2^30,最后就不用考虑小数的影响了。
72665192664
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/24 10:31
*/
public class C {
static long[][] weight = new long[31][31];//数值较大用long来存
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
long fac = 1;
fac <<= 30;
for (int i = 1; i <= 29; i++) {
for (int j = 1; j <= i; j++) {
weight[i][j] = scanner.nextLong();
weight[i][j] *= fac;
}
}
// scanner.nextLine();
for (int i = 1; i <= 30; i++) {
for (int j = 1; j <= i; j++) {
weight[i][j] += weight[i - 1][j - 1] / 2 + weight[i - 1][j] / 2;
}
}
long min = weight[30][1], max = weight[30][1];
for (int j = 1; j <= 30; j++) {
if (max < weight[30][j]) max = weight[30][j];
if (min > weight[30][j]) min = weight[30][j];
}
long ans = max / (min / 2086458231);
System.out.println(min);
System.out.println(max);
System.out.println(ans);
}
}
E.取数位
题目描述
求1个整数的第k位数字有很多种方法。
以下的方法就是一种。
public class Main {
static int len(int x) {
if (x < 10) return 1;
return len(x / 10) + 1;
}
// 取x的第k位数字
static int f(int x, int k) {
if (len(x) - k == 0) return x % 10;
return ______________________;
}
public static void main(String[] args) {
int x = 23513;
//System.out.println(len(x));
System.out.println(f(x, 3));
}
}
对于题目中的测试数据,应该打印5。
请仔细分析源码,并补充划线部分所缺少的代码。
注意:只提交缺失的代码,不要填写任何已有内容或说明性的文字。
题目分析
注意数字首位为第一位。
// 取x的第k位数字
static int f(int x, int k) {
if (len(x) - k == 0) return x % 10;
return f(x / 10, k);
}
F.最大公共子串
题目描述
最大公共子串长度问题就是:
求两个串的所有子串中能够匹配上的最大长度是多少。
比如:“abcdkkk” 和 “baabcdadabc”,
可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
下面的程序是采用矩阵法进行求解的,这对串的规模不大的情况还是比较有效的解法。
请分析该解法的思路,并补全划线部分缺失的代码。
public class Main {
static int f(String s1, String s2) {
char[] c1 = s1.toCharArray();
char[] c2 = s2.toCharArray();
int[][] a = new int[c1.length + 1][c2.length + 1];
int max = 0;
for (int i = 1; i < a.length; i++) {
for (int j = 1; j < a[i].length; j++) {
if (c1[i - 1] == c2[j - 1]) {
a[i][j] = __________________; //填空
if (a[i][j] > max) max = a[i][j];
}
}
}
return max;
}
public static void main(String[] args) {
int n = f("abcdkkk", "baabcdadabc");
System.out.println(n);
}
}
题目分析
一个DP问题,关键在于找到转换方程。下面用表格来演示。
| a | b | a | b | c | |
|---|---|---|---|---|---|
| a | 1 | 0 | 1 | 0 | 0 |
| b | 0 | 2 | 0 | 2 | 0 |
| c | 0 | 0 | 0 | 0 | 3 |
黄色表示第一个公共子串,蓝色表示第二个公共子串,分别为"ab",“abc”,长度为2,3。数字表示公共子串的长度。
由表格知,公共子串长度增加一定建立在对应位置元素相同的情况下,且数值为左上单元格数值加1。转换方程为
dp[i][j] = dp[i - 1][j - 1] + 1;
题解
public class Main {
static int f(String s1, String s2) {
char[] c1 = s1.toCharArray();
char[] c2 = s2.toCharArray();
int[][] a = new int[c1.length + 1][c2.length + 1];
int max = 0;
for (int i = 1; i < a.length; i++) {
for (int j = 1; j < a[i].length; j++) {
if (c1[i - 1] == c2[j - 1]) {
a[i][j] = a[i - 1][j - 1] + 1; //填空
if (a[i][j] > max) max = a[i][j];
}
}
}
return max;
}
public static void main(String[] args) {
int n = f("abcdkkk", "baabcdadabc");
System.out.println(n);
}
}
G.日期问题
题目描述
小明正在整理一批历史文献。这些历史文献中出现了很多日期。
小明知道这些日期都在1960年1月1日至2059年12月31日。
令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,
有采用月/日/年的,还有采用日/月/年的。更加麻烦的是,年份也都省略了前两位,
使得文献上的一个日期,存在很多可能的日期与其对应。
比如02/03/04,可能是2002年03月04日、2004年02月03日或2004年03月02日。
给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗
输入
一个日期,格式是"AA/BB/CC"。 (0 <= A, B, C <= 9)
输出
输出若干个不相同的日期,每个日期一行,格式是"yyyy-MM-dd"。多个日期按从早到晚排列。
输入样例
02/03/04
输出样例
2002-03-04
2004-02-03
2004-03-02
题目分析
一道日期计算问题,需要考虑闰年以及二月份天数问题,可以将每个日期看作字符串,去重,从早到晚排列,可以用TreeSet处理。
题解
import java.util.Scanner;
import java.util.TreeSet;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/27 10:36
*/
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
TreeSet<String> ans = new TreeSet<>();
String str = scanner.next();
int a = (str.charAt(0) - '0') * 10 + str.charAt(1) - '0';
int b = (str.charAt(3) - '0') * 10 + str.charAt(4) - '0';
int c = (str.charAt(6) - '0') * 10 + str.charAt(7) - '0';
String ans1 = myDate(a, b, c);//最多有三种日期
String ans2 = myDate(c, a, b);
String ans3 = myDate(c, b, a);
if (!ans1.equals("")) ans.add(ans1);
if (!ans2.equals("")) ans.add(ans2);
if (!ans3.equals("")) ans.add(ans3);
for (String s : ans) {
System.out.println(s);
}
}
public static boolean isyear(int year) {
return (year % 4 == 0 && year % 100 != 0) || year % 400 == 0;
}
public static String myDate(int a, int b, int c) {
int[] month = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};//补0使下标与月份对应上
if (0 <= a && a <= 59) a += 2000;
if (60 <= a && a <= 99) a += 1900;
if (isyear(a)) month[2] = 29;
if (b > 12 || b <= 0) return "";//不满足则返回空串
if (c > month[b] || c <= 0) return "";
String aa = "" + a;
String bb = "" + b;
String cc = "" + c;
if (bb.length() == 1) bb = "0" + bb;
if (cc.length() == 1) cc = "0" + cc;
return aa + "-" + bb + "-" + cc;
}
}
H.包子凑数
题目描述
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,
其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,
使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。
当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,
分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
输入样例1
2
4
5
输出样例1
6
输入样例2
2
4
6
输出样例2
INF
题目分析
有若干种数量不同的包子,每一种数量的包子有无限笼,这是一个完全背包问题,只是题目让求哪些数量没有办法凑出来。这是一道多个数的组合问题。在数论中,裴蜀定理给了解题的突破口。
裴蜀定理
在数论中,裴蜀定理是一个关于最大公约数(或最大公约式)的定理,裴蜀定理得名于法国数学家艾蒂安·裴蜀。
对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性不定方程(称为裴蜀等式):若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立,如果d不是1,那么必然有无限个数无法被组合出来。例如2 和 4,d = 2,所有的组合都是2的倍数,则所有的奇数都不能被表示出来。
当a,b互质时,即gcd(a,b) = 1,不能被表示出来的数有一个上界,上界为ab - a - b。
相关证明:a,b组合数不能表示的上界
题解
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/27 13:25
*/
public class Main {
static final int N = 105;
static int[] a = new int[N];
static boolean[] f = new boolean[10000];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
f[0] = true;//数量为0可以凑出来
int ans = 0, g = 0;//g为最大公因数
int n = scanner.nextInt();
for (int i = 1; i <= n; i++) {
a[i] = scanner.nextInt();
if (i == 1) g = a[i];//初始化最大公因数
else g = gcd(a[i], g);
for (int j = 0; j + a[i] < 10000; j++) {
if (f[j]) f[j + a[i]] = true;//如果数量j可以凑出来,加上一个增量也能凑出来
}
}
//无限个答案,打印"INF"并终止程序
if (g != 1) {
System.out.println("INF");
System.exit(0);
}
for (int i = 0; i < 10000; i++) {
if (!f[i]) ans++;
}
System.out.println(ans);
}
public static int gcd(int m, int n) {
if (m % n == 0) return n;
else return gcd(n, m % n);
}
}
H.买不到的数目【第四届】【省赛】【A组】(相关题目)
题目描述
小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入
两个正整数,表示每种包装中糖的颗数(都不多于1000)
输出
一个正整数,表示最大不能买到的糖数
输入样例1
4 7
输出样例1
17
输入样例2
3 5
输出样例2
7
题解
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/27 16:09
*/
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int a = scanner.nextInt();
int b = scanner.nextInt();
boolean[] f = new boolean[a * b + 1];
f[0] = true;
for (int i = 0; i + a < a * b; i++) {
if (f[i]) f[i + a] = true;
}
for (int i = 0; i + b < a * b; i++) {
if (f[i]) f[i + b] = true;
}
int max = -1;
for (int i = 0; i < a * b; i++) {
if (!f[i]) max = i;
}
System.out.println(max);
}
}
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/27 16:09
*/
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int a = scanner.nextInt();
int b = scanner.nextInt();
System.out.println(a * b - a - b);
}
}
I.分巧克力
题目描述
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:
- 形状是正方形,边长是整数
- 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力和2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。
输出
输出切出的正方形巧克力最大可能的边长。
输入样例
2 10
6 5
5 6
输出样例
2
题目分析
这道题网上有很多题都表示要用到二分,但是我没用二分也过了,可能有数据不强的原因。非二分解法:首先算得N个巧克力面积的总面积,对K作商得到可能的面积的最大值,则最大边长的平方小于等于单个面积的最大值。接着在依次遍历每一个可能的边长,如果可以分割的巧克力块数大于等于K,则更新最大值,而一旦小于K,则跳出循环。
题解
二分解法
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/28 10:39
*/
public class Main {
static class Chocolate {
int l, w;
Chocolate(int l, int w) {
this.l = l;
this.w = w;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
int sum = 0;
Chocolate[] cho = new Chocolate[n];
for (int i = 0; i < n; i++) {
int l, w;
l = scanner.nextInt();
w = scanner.nextInt();
cho[i] = new Chocolate(l, w);
}
int max = 0;
int l = 1, r = 100001;
while (l <= r) {
int mid = (l + r) / 2;
sum = 0;
for (int i = 0; i < n; i++) {
sum += (cho[i].l / mid) * (cho[i].w / mid);
}
if (sum >= k) {
l = mid + 1;
max = mid;
} else r = mid - 1;
}
System.out.println(max);
}
}
非二分解法
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/28 09:27
*/
public class Main {
static class Chocolate {
int l, w;
Chocolate(int l, int w) {
this.l = l;
this.w = w;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
int s = 0;
Chocolate[] cho = new Chocolate[n];
for (int i = 0; i < n; i++) {
int l, w;
l = scanner.nextInt();
w = scanner.nextInt();
cho[i] = new Chocolate(l, w);
s += l * w;
}
int max = 0;
for (int len = 1; len * len <= s / k; len++) {
int num = 0;
for (int i = 0; i < n; i++) {
num += (cho[i].l / len) * (cho[i].w / len);
if (num >= k) {
max = Math.max(max, len);
break;
}
}
if (num < k) break;
}
System.out.println(max);
}
}
J.K倍区间
题目描述
给定一个长度为N的数列,A1, A2, … AN,
如果其中一段连续的子序列Ai, Ai+1, … Aj(i <= j)之和是K的倍数,
我们就称这个区间[i, j]是K倍区间。
你能求出数列中总共有多少个K倍区间吗?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100000)
输出
输出一个整数,代表K倍区间的数目。
输入样例
5 2
1
2
3
4
5
输出样例
6
题目分析
解决一个问题需要先找到一个可行解,再逐步优化。一开始先暴力枚举,之后再进行优化。枚举起点i和终点j,再对[i,j]之间的数字求和,判断是否为K的倍数。这样就是三重for循环,时间复杂度为O(N^3),在本题下会超时。接着进行第一步优化,算区间和可以引入前缀和,例如s[i]表示i前的元素之和,s[j]表示j前的元素之和,s[j] - s[i-1]表示[i,j]之间的数字和,这样可以用O(1)的复杂度算出区间和,时间复杂度优化O(N^2),但这依然会超时,继续进行优化。不难想到,如果两个数对另一个数取模同余,那么这两个数的差必然是这个模数的整数倍。请看下列表格:
| index | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| a | 0 | 1 | 2 | 3 | 4 | 5 |
| s | 0 | 1 | 3 | 6 | 10 | 15 |
| s%k | 0 | 1 | 1 | 0 | 0 | 1 |
在这里引入一个mod数组,保存每一种余数的值,在余数相同的数里面选择两个,则这两个数的差便是K的倍数。在上面的表格中,s[1]、s[2]和s[5]的余数相同,余数都为1,即mod[1] = 3,3个里面选两个,有C32种情况,有3种情况,余数为2有两种情况,s[3],s[4],C22 = 1,这样加起来答案是4,而不是6。出这种问题主要是边界0是否考虑到,我们算余数相同的情况有几种,然后作差,但是余数为0的时候缺了一种情况,s[3] s[4] s[4]-s[3] 可以看作是
s[3] - s[0] 、s[4] - s[0] 、s[4]-s[3] ,这样加上s[0]的话,mod[0] = 3 ,2 * C32 = 6,结果正确,所以一开始要将mod[0] = 1。这样就将时间复杂度降为了O(N),同时在计算过程中要考虑运算结果超限制的情况。
题解
import java.util.Scanner;
/**
* @Description
* @Author:PrinceHan
* @CreateTime:2022/1/28 10:48
*/
public class Main {
static final int N = 100005;
static int[] s = new int[N];
static long[] mod = new long[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
long ans = 0;
mod[0] = 1;
for (int i = 1; i <= n; i++) {
s[i] = scanner.nextInt();
s[i] += s[i - 1];
s[i] %= k;
mod[s[i]]++;
}
for (int i = 0; i < n; i++) {
ans += mod[i] * (mod[i] - 1) / 2;
}
System.out.println(ans);
}
}