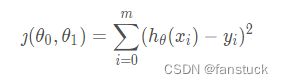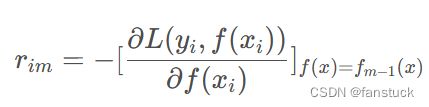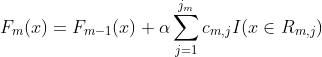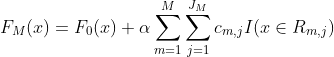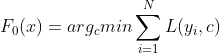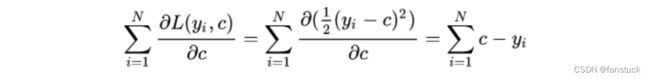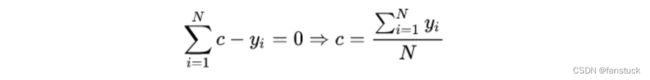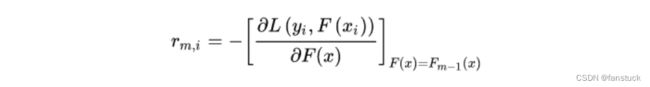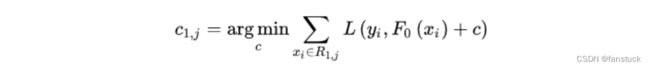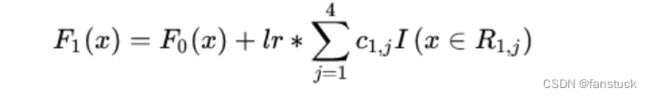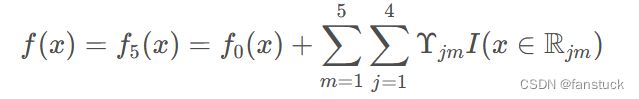一文速学-GBDT模型算法原理以及实现+Python项目实战
目录
前言
一、GBDT算法概述
1.决策树
2.Boosting
3.梯度提升
使用梯度上升找到最佳参数
二、GBDT算法原理
1.计算原理
2.预测原理
三、实例算法实现
1.模型训练阶段
1）初始化弱学习器
2）对于建立M棵分类回归树：
四、Python实现
1.原始决策树累积
2.sklearn
前言
上篇文章内容已经将Adaboost模型算法原理以及实现详细讲述实践了一遍，但是只是将了Adaboost模型分类功能，还有回归模型没有展示，下一篇我将展示如何使用Adaboost模型进行回归算法训练。首先还是先回到梯度提升决策树GBDT算法模型上面来，GBDT模型衍生的模型在其他论文研究以及数学建模比赛中十分常见，例如XGBoost，LighGBM，catboost。其实将这些算法重要的点拿出来就更容易理解了，主要是五个方向的变动改进:
| 算法差异点 | GBDT | XGBoost | LightGBM | CatBoost |
| 弱学习器 | CART回归树 | 1.CART回归树 2.线性学习器 3.Dart树 |
Leaf-wise树 | 对称树 |
| 寻找分裂点 | 贪心算法 | 近似算法 | 直方图算法 | 预排序算法 |
| 稀疏值处理 | 无 | 稀疏感知算法 | EFB(互斥特征捆绑) | 无 |
| 类别特征 | 不直接支持，可自行编码后输入模型 | 同GBDT | 直接支持，GS编码 | 直接支持，Ordered TS编码 |
| 并行支持 | 不可以 | 可以 | 可以 | 可以 |
本篇主讲GBDT算法模型以及应用，先把大体框架熟悉，之后的算法只需要填补功能就好了。本篇并不会提及太多专业公式以及推论公式，数学基础薄弱的不用担心，大家可以放心学习，我会尽可能简单易懂的讲明白算法原理，主要是实战以及运用和相关代码的使用。
一、GBDT算法概述
在开篇Boosting算法中有过讲到，回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。
GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。
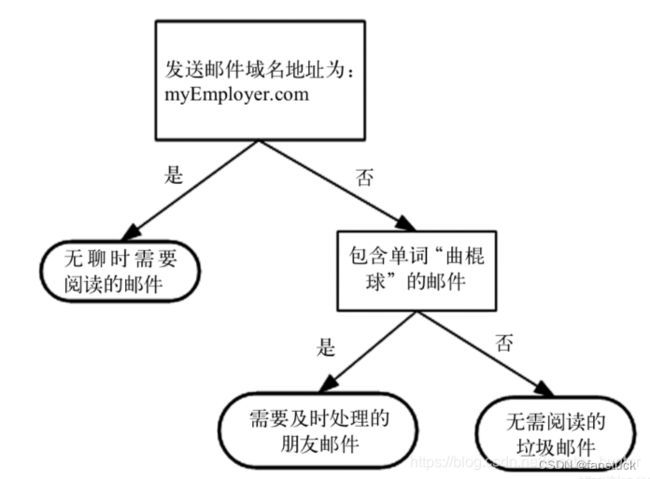
1.决策树
那么GBDT算法肯定有其对应的弱学习器，也就是CART回归树。
这里如果大家之前并没有了解过决策树的概念，可以去看我的这篇文章：
一文速学数模-分类模型(二)决策树(Decision Tree）算法详解及python实现
那么这个CART指的是（Classification and Regression Tree）的意思， 这里我大体讲述一下该决策树算法：，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。
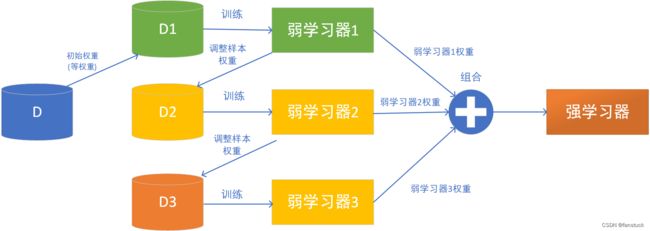
2.Boosting
Boosting的思路则是串行的，每一次训练一个模型都是建立在前一个模型的学习基础上，不断去通过新模型去减少之前的错误。
这点思路在讲AdaBoosting算法模型时候已经讲的很明确了，一图就可了解：
3.梯度提升
在梯度提升中，每个弱学习器的训练都是基于前一个弱学习器的预测误差，通过梯度下降的方式来最小化误差。具体来说，对于回归问题，我们可以选择平方损失函数作为损失函数。
关于梯度提升算法我之前在Logistic原理详解和遗传算法里面也有详解讲过，此类最优算法最核心的一点就是对于残差的使用。而损失函数就是衡量调整每一次迭代模型算法的权重的参考功能。
损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于样本
,采用线性回归，损失函数为：
对于分类问题，则可以选择交叉熵损失函数。在每次迭代中，我们都会训练一个新的弱学习器，使得它能够最大程度地减少当前模型的误差。然后将这个新的学习器加入到当前的模型中，从而不断提升整个模型的预测能力。
使用梯度上升找到最佳参数
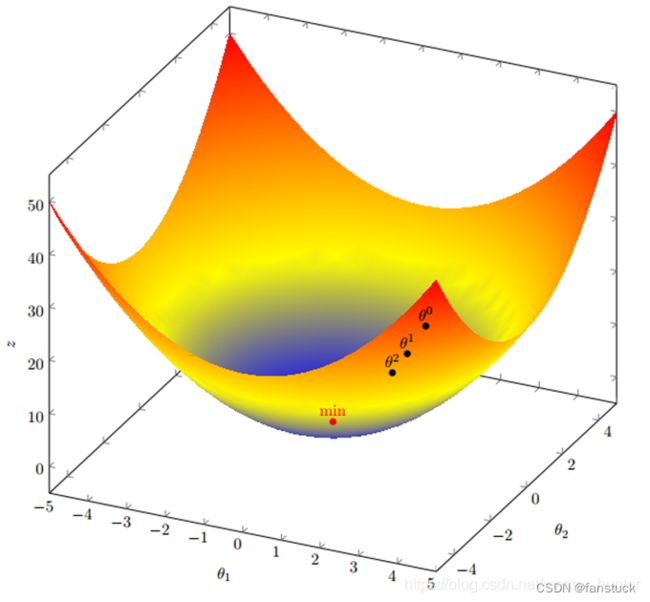
使用梯度上升找到最佳参数可以假设为爬山运动，我们总是往向着山顶的方向攀爬，当爬到一定角度以后也会驻足停留下观察自身角度是否是朝着山顶的角度上攀爬。并且我们需要总是指向攀爬速度最快的方向爬。
要找到某函数的最大值，最好的方法就是沿着该函数的梯度方向搜寻。我们假设步长为
，用向量来表示的话，梯度上升算法的迭代公式如下：
。该公式停止的条件是迭代次数达到某个指定值或者算法达到某个允许的误差范围。
梯度提升的一个重要特点是它可以应用于各种类型的弱学习器，例如决策树、线性模型、神经网络等。然而，决策树是梯度提升中最常用的弱学习器之一，因为它们可以很好地处理非线性特征和交互作用，同时也可以通过剪枝等技术来避免过拟合。
二、GBDT算法原理
1.计算原理
GBDT算法的原理如下：
-
初始化。将所有样本的权重设置为相等的值，建立一个初始模型作为基准模型，可以设置为简单的平均值或者是中位数。例如建立一个弱分类器
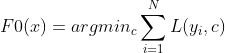,c即为平均值。 -
迭代训练。在每一轮迭代中，GBDT算法会先根据当前模型的预测结果计算每个样本的残差。对于回归问题，残差就是实际输出值与模型预测值之间的差异，对于分类问题，残差就是样本的实际类别与模型预测类别之间的差异。然后，GBDT会训练一个新的决策树模型，来学习如何预测这些残差。对于建立M棵CART树m=1,2,...M:
-
对i=1,2,...,N, 计算第m棵树对应的响应值(损失函数的负梯度)：
-
对于i = 1,2,...N,利用CART回归树拟合数据，得到第m棵回归树，其对应的叶子节点区域为
，其中j=1,2,...,
，且为第m棵回归叶子节点的个数。 -
对于
个叶子节点区域j=1,2,...,,计算最佳拟合值
-
更新强学习器
:
-
-
添加新模型。新模型的预测结果会被加入到当前模型的输出中，使得模型的预测结果逐步趋近于真实值。可以将每个模型的输出进行加权求和，得到最终模型的输出。
-
终止条件。当模型的准确率达到一定阈值，或者迭代次数达到预设的最大值时，算法停止迭代。最后得到强学习器表达式:
GBDT算法通过不断训练新的决策树模型，并将它们的预测结果累加到当前模型的输出中，来逐步提升整个模型的预测能力。与传统的决策树算法相比，GBDT算法可以减少过拟合的风险，并且具有较强的鲁棒性。
2.预测原理
上述模型生成原理的数学推论和公式是绕不开的，其他算法模型也是一样，在所有的机器学习以及其他算法模型中来说，没有不存在数学公式的模型。但是预测原理我们可以尽可能简化，这里参考GBDT的原理和应用的举例比较形象：
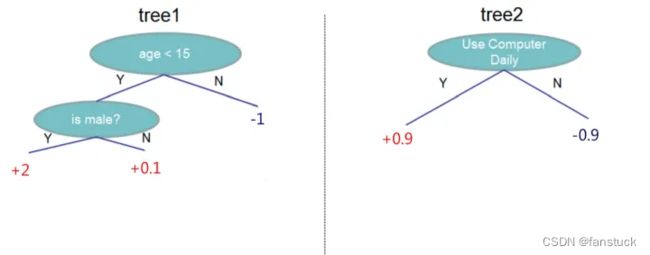
假设我们要预测一个人是否会喜欢电脑游戏，特征包括年龄，性别是否为男，是否每天使用电脑。标记（label）为是否喜欢电脑游戏，假设训练出如下模型：
该模型又两棵树组成， tree1使用 age < 15 和 is male 作为内节点，叶子节点是输出的分数。 tree2使用是否每日使用电脑作为根节点。假设测试样本如下：
最后对某样本累加它所在的叶子节点的输出值，例如：
单独的使用GBDT模型，容易出现过拟合，在实际应用中往往使用 GBDT＋LR的方式做模型训练。
三、实例算法实现
首先我们以一组数据作为训练集：
| 编号 | 车辆速度 | 道路等级 | 拥堵状态 |
| 0 | 20 | 1 | 5 |
| 1 | 30 | 2 | 4 |
| 2 | 60 | 3 | 2 |
| 3 | 70 | 4 | 2 |
测试数据如下表所示：
| 编号 | 车辆速度 | 道路等级 | 拥堵状态 |
| 0 | 50 | 3 | ？ |
1.模型训练阶段
参数设置：
-
学习率：learning_rate = 0.3
-
迭代次数：n_trees = 6
-
树的深度：max_depth = 3
1）初始化弱学习器
损失函数为平方损失，因为平方损失函数是一个凸函数，可以直接求导，令导数等于零，得到
:
令导数等于0：
所以初始化时，
取值为所有训练样本标签值的均值。
,此时得到的初始化学习器为
2）对于建立M棵分类回归树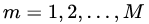
：
由于我们设置了迭代次数：n_trees=6，这就是设置了M=6。
首先计算负梯度，根据上文损失函数为平方损失时，负梯度就是残差，也就是
与上一轮得到的学习器
的差值：
现将残差的计算结果列表如下：
| 编号 | 真实值 |  |
残差 |
| 0 | 5 | 3.25 | 1.75 |
| 1 | 4 | 3.25 | 0.75 |
| 2 | 2 | 3.25 | -1.25 |
| 3 | 2 | 3.25 | -1.25 |
此时将残差作为样本的真实值来训练弱学习器
，即下表数据：
| 编号 | 车辆速度 | 道路等级 | 拥堵状态 |
| 0 | 20 | 1 | 1.75 |
| 1 | 30 | 2 | 0.75 |
| 2 | 60 | 3 | -0.25 |
| 3 | 70 | 4 | -1.25 |
遍历每个特征的每个可能取值。从车辆速度为20开始，到道路等级特征为4结束，分别计算分裂后两组数据的平方损失（Square Error）， 
为左节点的平方损失，
为右节点的平方损失，找到使平方损失和 
最小的那个划分节点，即为最佳划分节点。
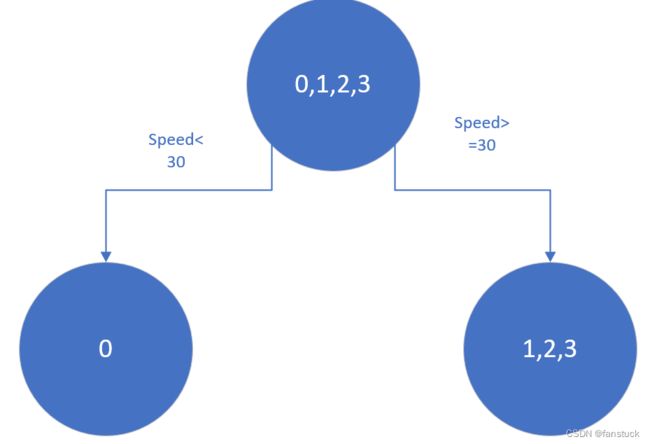
例如：以车辆速度为30划分节点，将小于30的样本划分为左节点，大于等于30的样本划分为右节点。
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 |  |
 |
 |
| 车辆速度20 | / | 0,1,2,3 | 0 | 5.25 | 5.25 |
| 车辆速度30 | 0 | 1,2,3 | 0 | 2.1875 | 2.1875 |
| 车辆速度60 | 0,1 | 2,3 | ... | ||
| 车辆速度70 | 0,1,2 | 3 | |||
| 道路等级1 | / | 0,1,2,3 | |||
| 道路等级2 | 0 | 1,2,3 | |||
| 道路等级3 | 0,1 | 2,3 | |||
| 道路等级4 | 0,1,2 | 3 | 3.675625 | 0 | 3.675625 |
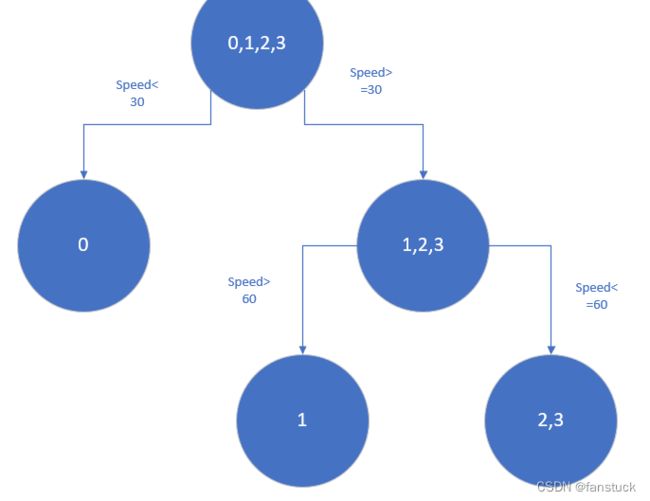
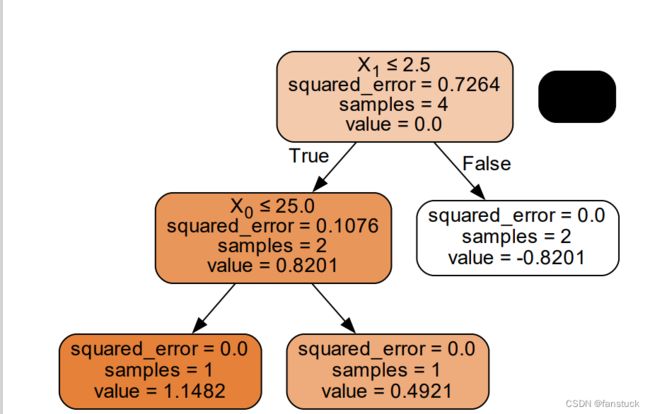
以上划分点的总平方损失最小有两个划分点：车辆速度30和道路等级3.所以随机选一个作为划分点，这里我们选车辆速度30：
我们设置的参数中树的深度max_depth=3，现在树的深度只有2，需要再进行一次划分，这次划分要对左右两个节点分别进行划分：
此时我们的树深度满足了设置，还需要做一件事情，给这每个叶子节点分别赋一个参数
，来拟合残差。
这里其实和上面初始化弱学习器是一样的，对平方损失函数求导，令导数等于零，化简之后得到每个叶子节点的参数
，其实就是标签值的均值。这个地方的标签值不是原始的
，而是本轮要拟合的标残差
。
此时可更新强学习器，需要用到参数学习率：learning_rate=0.1，用
表示。更新公式为：
为什么要用学习率呢？这是Shrinkage的思想,如果每次都全部加上拟合值 
，即学习率为1，很容易一步学到位导致GBDT过拟合。
重复此步骤，最后生成5棵树。
得到最后的强学习器：
四、Python实现
1.原始决策树累积
如果安装我们上一步这样原生计算推论的话，那么代码应该这样写：
from sklearn.tree import DecisionTreeRegressor
import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
import pandas as pd
import pydotplus
from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz
import os
os.environ["Path"] += os.pathsep + 'D:/Graphviz/bin'
data_1=[[20,1,5],[30,2,4],[60,3,2],[70,4,2]]
data=pd.DataFrame(data_1,columns=['speed','kind','state'])
X=np.array(data.iloc[:,:-1]).reshape((-1,2))
y=np.array(data.iloc[:,-1]).reshape((-1,1))
tree_reg1 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg1.fit(X, y)
y2 = y - np.array([3.25]*4).reshape((-1,1))
tree_reg2 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg2.fit(X, y2)
y3 = y2 - 0.1*np.array(tree_reg2.predict(X)).reshape((-1,1))
tree_reg3 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg3.fit(X, y3)
y4 = y3 - 0.1*np.array(tree_reg3.predict(X)).reshape((-1,1))
tree_reg4 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg4.fit(X, y4)
y5 = y4 - 0.1*np.array(tree_reg4.predict(X)).reshape((-1,1))
tree_reg5 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg5.fit(X, y5)
y6 = y5 - 0.1*np.array(tree_reg5.predict(X)).reshape((-1,1))
tree_reg6 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg6.fit(X, y6)
2.sklearn
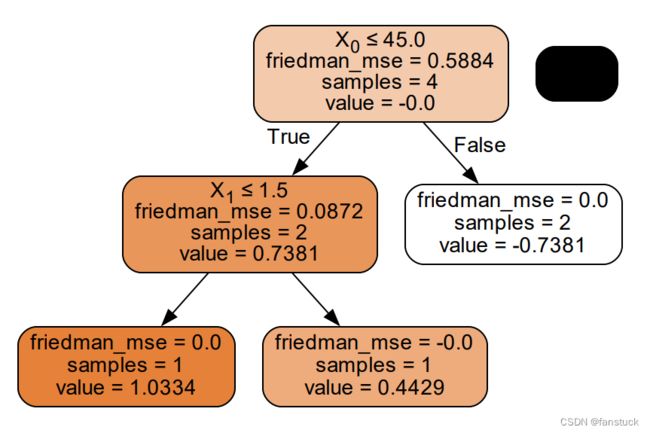
使用sklearn的话：
estimator=GradientBoostingRegressor(random_state=10)
estimator.fit(data.iloc[:,:-1],data.iloc[:,-1])
dot_data = export_graphviz(estimator.estimators_[5,0], out_file=None, filled=True, rounded=True, special_characters=True, precision=4)
graph = pydotplus.graph_from_dot_data(dot_data)
二者树不同是因为参数学习率以及树的深度，迭代次数不一致导致，无碍。
那么我们现在拿预测样本来使用：
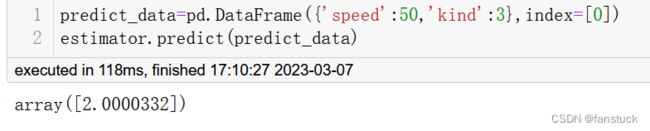
predict_data=pd.DataFrame({'speed':50,'kind':3},index=[0])
estimator.predict(predict_data)
至此模型建立完毕，那么让我们总结一下GBDT模型特性：
AdaBoost和GBDT都是重复选择一个表现一般的模型并且每次基于先前模型的表现进行调整。不同的是，AdaBoost是通过调整错分数据点的权重来改进模型，GBDT是通过计算负梯度来改进模型。因此，相比AdaBoost, GBDT可以使用更多种类的目标函数，而当目标函数是均方误差时，计算损失函数的负梯度值在当前模型的值即为残差。
GBDT的求解过程就是梯度下降在函数空间中的优化过程。在函数空间中优化，每次得到增量函数，这个函数就是GBDT中一个个决策树，负梯度会拟合这个函数。要得到最终的GBDT模型，只需要把初始值或者初始的函数加上每次的增量即可。