0203优先级下的调度问题_环_拓扑排序-有向图-数据结构和算法(Java)
1 概述
在和有向图相关的实际应用中,有向环特别的重要。在实际应用中,一般只会重点关注其中的一小部分,或者只想知道它们是否存在。
2 调度问题
一种应用广泛的模型是给定一组任务并安排它们的执行顺序,限制条件是这些任务的执行方法和起始时间,也可能是任务的时耗即消耗的其他资源。最重要的一种限制条件叫做优先级限制。
优先级限制下的调度。 给定一组需要完成的任务,以及一组关于任务完成的先后次序的优先级限制。在满足限制条件的前提下如何安排并完成所有的任务?
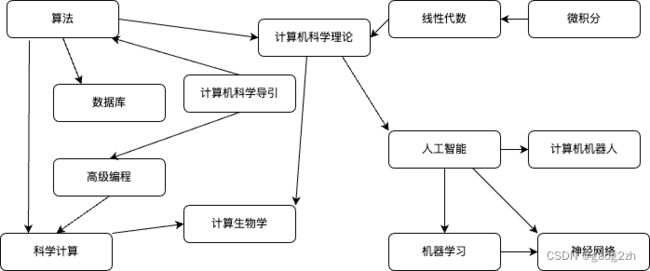
以一个正在安排课程的大学生为例,有些课程是其他课程的先导课程,如下图2-1所示:
顶点对应任务,有向边对应优先级顺序,使用整数位顶点的编号的标准模型来表示这个示例,如下图2-2所示:
在有向图中,优先级限制下的调度问题等价于下面这个基本问题。
拓扑排序。给定一幅有向图,将所有的顶点排序,使得所有的有向边均从排在前面的元素指向排在后面的元素。(或者说明无法做到这一点)
上面大学生课程示例对应的拓扑排序,如下图2-3所示:
2 有向图中的环
2.1 概念
如果一个有优先级限制的问题中存在有向环,那么这个问题肯定是无解的。
有向环检测。给定的有向图中包含有向环吗?如果有,按照路径的方向从某个顶点返回自己来找到环上的的所有顶点。
2.2 算法
- 基于深度优先搜索由我们维护的栈表示正式“当前”正在遍历的所有有向路径;
- 一旦我们找到一条有向边v->w且w已存在于栈中,就找到一个环;
- 因为栈表示的是一条由w到v的有向路径,而v->w正好补全了这个环。
- 如果没有找到这样的边,说明这幅有向图上无环的。
2.3 实现
- API 如下表2.3-1所示:
| public class | DirectedCycle | |
|---|---|---|
| DirectedCycle(Digraph digraph) | 选择有向环的构造函数 | |
| public boolean | hascycle() | 是否含有有向环 |
| public Iterable |
cycle() | 有向环中所有顶点;没有返回null |
非递归实现如下代码2.3-1所示:
package com.gaogzhen.datastructure.graph.directed;
import com.gaogzhen.datastructure.graph.undirected.Entry;
import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Digraph;
import java.util.Iterator;
/**
* 检测有向环
* @author gaogzhen
*/
public class DirectedCycle {
/**
* 标记
*/
private boolean[] marked;
/**
* 指向起点的有向路径
*/
private int[] edgeTo;
/**
* 当前栈上顶点
*/
private boolean[] onStack;
/**
* 有向环
*/
private Stack<Integer> cycle;
/**
* 检测有向环
* @param digraph 有向图
*/
public DirectedCycle(Digraph digraph) {
marked = new boolean[digraph.V()];
onStack = new boolean[digraph.V()];
edgeTo = new int[digraph.V()];
for (int v = 0; v < digraph.V(); v++) {
if (!marked[v] && cycle == null) {
dfs(digraph, v);
}
}
}
/**
* 深度优先检测有向环
* @param digraph 有向图
* @param s 起点
*/
private void dfs(Digraph digraph, int s) {
Stack<Entry<Integer, Iterator<Integer>>> path = new Stack<>();
// marked[v] = true;
if (!marked[s]) {
// 键值对起点-起点对应邻接表迭代器压入栈中
marked[s] = true;
onStack[s] = true;
Iterable<Integer> iterable = digraph.adj(s);
Iterator<Integer> it;
if (iterable != null && (it = iterable.iterator()) != null){
path.push(new Entry<>(s, it));
}
}
deepLevel:
while (!path.isEmpty()) {
Entry<Integer, Iterator<Integer>> entry = path.pop();
int x;
Iterator<Integer> it = entry.getValue();
Integer f = entry.getKey();
while (it.hasNext()) {
// 当前顶点对应的邻接表迭代器还有元素,获取下一个元素
x = it.next();
if (cycle != null) {
return;
} else if (!marked[x]) {
// 顶点未被标记,标记顶点且标记路径x->f
// f是x所在邻接表对应的顶点
marked[x] = true;
onStack[x] = true;
edgeTo[x] = f;
// if (it.hasNext()) {
// 邻接表迭代器还有元素,重新压入栈
path.push(entry);
// }
// 按照深度优先原则,把新标记顶点对应的键值对压入栈中,在下次循环时优先访问
Iterable<Integer> iterable = digraph.adj(x);
if (iterable != null && (it = iterable.iterator()) != null){
path.push(new Entry<>(x, it));
}
continue deepLevel;
} else if (onStack[x]) {
// 存在有向环
// 遍历有向路径,构建有向环
cycle = new Stack<>();
for (int i = f; i != x ; i = edgeTo[i]) {
cycle.push(i);
}
cycle.push(x);
cycle.push(f);
}
}
onStack[f] = false;
}
}
/**
* 是否存在有向环
* @return {@code true} 存在有向环, {@code false} 否则
*/
public boolean hasCycle() {
return cycle != null;
}
/**
* 返回有向环
*/
public Iterable<Integer> cycle() {
return cycle;
}
/**
* 证明确实有有向环
* @return {@code true} 确实存在一个有向环, {@code false}否则
*/
private boolean check() {
if (hasCycle()) {
// verify cycle
int first = -1, last = -1;
for (int v : cycle()) {
if (first == -1) {
first = v;
}
last = v;
}
if (first != last) {
System.err.printf("cycle begins with %d and ends with %d\n", first, last);
return false;
}
}
return true;
}
}
说明:
- onStack[]表示当前在栈上的顶点,首次访问设置true;当顶点对应的邻接表访问完毕,该结点会退出当前栈,设置为false。
- continue deepLevel;我们是实用非递归的深度优先搜索算法,当邻接表有未访问的顶点时,表示我们需要优先访问下一层的顶点,但是当前顶点不退出当前栈。
- // if (it.hasNext()) { 在之前的代码中我们这里放开,表示当前邻接表没有元素,不在放入栈中;但是这里注释掉,因为我们需要外围的while循环判断是否邻接表已经遍历完毕,设置onStack[]对应顶点为false。按照逻辑,不能出现有下层结点在栈中而父结点退出栈的情况。
2.4 测试
测试代码2.4-1如下所示:
public static void testDirectedCycle() {
String path = System.getProperty("user.dir") + File.separator + "asserts/tinyDAG.txt";
In in = new In(path);
Digraph digraph = new Digraph(in);
System.out.println(digraph.adj(10));
DirectedCycle cycle = new DirectedCycle(digraph);
System.out.println(cycle);
int v = 0;
System.out.println(cycle.hasCycle());
System.out.println(cycle.cycle());
}
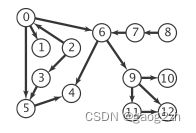
测试用有向图2数据在代码仓库中有,结构如下2.4-1所示
测试结果如下2.4-1所示:
com.gaogzhen.datastructure.graph.directed.DirectedCycle@3764951d
true
[7, 6, 9, 10, 7]
命题E。当且仅当一幅有向图时无环图时它才能进行拓扑排序。
证明。当一幅有向图含有一个环时,它就不可能时拓扑排序的。
3 顶点的深度优先次序
基于深度优先的顶点排序。它的思想时深度优先搜索正好只会访问每个顶点一次。如果将遍历的顶点参数保存在一个数据结构中,遍历这个数据结构就可以访问图中的所有顶点,遍历的顺序取决于数据结构的性质以及在递归(非递归栈)调用之前还是之后进行保存。
典型的应用中,顶点有3种排列顺序:
- 前序:在递归调用(加入非递归栈)之前将顶点加入队列。
- 后序:在递归调用(加入非递归栈)之后将顶点加入队列。
- 逆后序:在递归调用(加入非递归栈)之后将顶点加入栈。
顶点深度优先次序类DepthFirstOrder类,API如下表3-1所示:
| public class | DepthFirstOrder | |
|---|---|---|
| DepthFirstOrder(Digraph digraph) | 深度优先顶点排序构造函数 | |
| public Iterable |
pre() | 深度优先的前序排列 |
| public int | pre(int v) | 顶点v前序排列索引 |
| public Iterable |
post() | 深度优先的后序排列 |
| public int | post(int v) | 顶点v后序排列索引 |
| public Iterable |
reversePost() | 深度优先的逆后序排列 |
非递归实现代码3-1如下所示:
package com.gaogzhen.datastructure.graph.directed;
import com.gaogzhen.datastructure.graph.undirected.Entry;
import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.*;
import java.util.Iterator;
/**
* 基于深度优先的顶点排序
* @author gaogzhen
*/
public class DepthFirstOrder {
/**
* 顶点已访问标记
*/
private boolean[] marked;
/**
* 基于深度优先的顶点前序排列索引
*/
private int[] pre;
/**
* 基于深度优先的顶点后序排序索引
*/
private int[] post;
/**
* 基于深度优先的顶点前序排列
*/
private Queue<Integer> preOrder;
/**
* 基于深度优先的后序排列
*/
private Queue<Integer> postOrder;
/**
* 当前前序顶点计数
*/
private int preCounter;
/**
* 当前后序顶点计数
*/
private int postCounter;
/**
* 深度优先的顶点排序
* @param digraph 有向图
*/
public DepthFirstOrder(Digraph digraph) {
pre = new int[digraph.V()];
post = new int[digraph.V()];
postOrder = new Queue<Integer>();
preOrder = new Queue<Integer>();
marked = new boolean[digraph.V()];
for (int v = 0; v < digraph.V(); v++) {
if (!marked[v]) {
dfs(digraph, v);
}
}
assert check();
}
/**
* 有向图的深度优先顶点排序
* @param digraph 有向图digraph
* @param v 起点
*/
private void dfs(Digraph digraph, int v) {
Stack<Entry<Integer, Iterator<Integer>>> path = new Stack<>();
// marked[v] = true;
if (!marked[v]) {
// 键值对起点-起点对应邻接表迭代器压入栈中
marked[v] = true;
pre[v] = preCounter++;
preOrder.enqueue(v);
Iterable<Integer> iterable = digraph.adj(v);
Iterator<Integer> it;
if (iterable != null && (it = iterable.iterator()) != null){
path.push(new Entry<>(v, it));
}
}
// 保证深度优先跳转标记
nextLevel:
while (!path.isEmpty()) {
Entry<Integer, Iterator<Integer>> entry = path.pop();
int x;
Iterator<Integer> it = entry.getValue();
Integer f = entry.getKey();
while (it.hasNext()) {
// 当前顶点对应的邻接表迭代器还有元素,获取下一个元素
x = it.next();
if (!marked[x]) {
// 顶点未被标记,标记顶点且标记路径x->f
// f是x所在邻接表对应的顶点
marked[x] = true;
pre[x] = preCounter++;
preOrder.enqueue(x);
// if (it.hasNext()) {
// 邻接表迭代器还有元素,重新压入栈
path.push(entry);
// }
// 按照深度优先原则,把新标记顶点对应的键值对压入栈中,在下次循环时优先访问
Iterable<Integer> iterable = digraph.adj(x);
if (iterable != null && (it = iterable.iterator()) != null){
path.push(new Entry<>(x, it));
}
// 保证深度优先:下一层有未访问结点,优先访问下层结点
continue nextLevel;
}
}
// 顶点f对应的邻接表访问完毕,后序排列开始记录
postOrder.enqueue(f);
post[f] = postCounter++;
}
}
/**
* 返回指定顶点v在前序排列中的索引
* @param v 指定顶点v
* @return 指定顶点v在前序排列中的索引
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int pre(int v) {
validateVertex(v);
return pre[v];
}
/**
* 返回顶点v在后序排列中的索引
* @param v 顶点v
* @return 顶点v在后序排列中的索引
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int post(int v) {
validateVertex(v);
return post[v];
}
/**
* 返回顶点的后序排列
*/
public Iterable<Integer> post() {
return postOrder;
}
/**
* 返回顶点的前序排列
*/
public Iterable<Integer> pre() {
return preOrder;
}
/**
* 返回顶点的逆后序排列
*/
public Iterable<Integer> reversePost() {
Stack<Integer> reverse = new Stack<Integer>();
for (int v : postOrder) {
reverse.push(v);
}
return reverse;
}
/**
* 校验前序和后序排列结果是否和pre(v)与post(v)相等
* @return {@code true}结果一致;{@code false}有一个不相等
*/
private boolean check() {
// check that post(v) is consistent with post()
int r = 0;
for (int v : post()) {
if (post(v) != r) {
StdOut.println("post(v) and post() inconsistent");
return false;
}
r++;
}
// check that pre(v) is consistent with pre()
r = 0;
for (int v : pre()) {
if (pre(v) != r) {
StdOut.println("pre(v) and pre() inconsistent");
return false;
}
r++;
}
return true;
}
/**
* 校验顶点v
* @param v 顶点v
*/
private void validateVertex(int v) {
int V = marked.length;
if (v < 0 || v >= V) {
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
}
}
测试用有向图数据3-1同之前一样,如下所示:
13
15
2 3
0 6
0 1
2 0
11 12
9 12
9 10
9 11
3 5
8 7
5 4
0 5
6 4
6 9
7 6
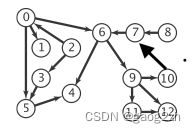
测试用有向图如下图3-1所示:
测试代码如下3-2所示:
public static void testDepthFirstOrder() {
String path = System.getProperty("user.dir") + File.separator + "asserts/tinyDGO.txt";
In in = new In(path);
Digraph digraph = new Digraph(in);
DepthFirstOrder depthFirstOrder = new DepthFirstOrder(digraph);
System.out.println(depthFirstOrder);
System.out.println("前序排列:" + depthFirstOrder.pre());
System.out.println("后序排列:" + depthFirstOrder.post());
System.out.println("逆后序排列:" + depthFirstOrder.reversePost());
int v = 4;
System.out.println("顶点:" + v + " 前序排列索引 " + depthFirstOrder.pre(v));
System.out.println("顶点:" + v + " 后序排列索引 " + depthFirstOrder.post(v));
}
测试结果:
后序排列:4 5 1 12 11 10 9 6 0 3 2 7 8
逆后序排列:[8, 7, 2, 3, 0, 6, 9, 10, 11, 12, 1, 5, 4]
顶点:4 前序排列索引 2
顶点:4 后序排列索引 0
4 拓扑排序
拓扑排序API如下表4-1所示:
| public class | Topological | |
|---|---|---|
| Topological(Digraph digraph) | 拓扑排序的构造函数 | |
| public boolean | hasOrder() | digraph可拓扑排序吗 |
| public Iterable |
order() | 顶点的拓扑排序 |
| public int | rank(int v) | 顶点v在拓扑排序中的索引 |
非递归实现代码如下4-1所示:
package com.gaogzhen.datastructure.graph.directed;
import edu.princeton.cs.algs4.Digraph;
/**
* 拓扑排序
* @author gaogzhen
*/
public class Topological {
/**
* 顶点的拓扑排序
*/
private Iterable<Integer> order;
/**
* 顶点在拓扑排序中索引
*/
private int[] rank;
/**
* 构建有向图digraph拓扑排序
*/
public Topological(Digraph digraph) {
DirectedCycle finder = new DirectedCycle(digraph);
if (!finder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(digraph);
order = dfs.reversePost();
rank = new int[digraph.V()];
int i = 0;
for (int v : order) {
rank[v] = i++;
}
}
}
/**
* 返回顶点的拓扑排序,没有返回null
* @return 顶点的拓扑排序,没有返回null
*/
public Iterable<Integer> order() {
return order;
}
/**
* 是否可拓扑排序
* @return {@code true} 可以拓扑排序,同时说明是有向无环图;{@code false}否则
*/
public boolean hasOrder() {
return order != null;
}
/**
* 指定顶点v在拓扑排序中索引
* @param v 指定顶点v
* @return 顶点v在拓扑排序中索引
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int rank(int v) {
validateVertex(v);
if (hasOrder()) {
return rank[v];
} else {
return -1;
}
}
/**
* 校验顶点v是否索引越界
* @param v 指定顶点
*/
private void validateVertex(int v) {
int V = rank.length;
if (v < 0 || v >= V) {
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
}
}
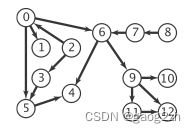
以#4中的有向图为例,测试代码如下;
public static void testTopological() {
String path = System.getProperty("user.dir") + File.separator + "asserts/tinyDGO.txt";
In in = new In(path);
Digraph digraph = new Digraph(in);
Topological topological = new Topological(digraph);
System.out.println(topological);
System.out.println("是否可拓扑排序(是否是有向无环图):" + topological.hasOrder());
System.out.println("拓扑排序:" + topological.order());
int v = 4;
System.out.println("顶点:" + v + " 拓扑排列索引 " + topological.rank(v));
}
测试结果:
是否可拓扑排序(是否是有向无环图):true
拓扑排序:[8, 7, 2, 3, 0, 6, 9, 10, 11, 12, 1, 5, 4]
顶点:4 拓扑排列索引 12
命题F。一幅有向无环图的拓扑顺序即为所有顶点的逆后序排列。
证明。对于任意边v->w,在访问v(递归dfs(v))时,下面三种情况比有其一成立。
- w已经被访问过且已放入队列(w已经被标记)
- w还没有被访问(未标记),因此v->w会直接或者间接访问w且加入队列,w会在v之前加入队列。
- w已经被访问但未加入队列。
证明的关键在于,在有向无环图中这种情况时不可能出现的。这是由于栈访问顺序 意味着存在从w到v的路径,但存在v->w则表示存在一个环。
在两种可能的情况中,w都会在v之前加入队列,因此在后序排列中w排在v之前而逆后序中w排在v之后。因此任意一条边v->w都如我们所愿地从排名较前顶点指向排名较后的顶点。
命题G。使用深度优先搜索对有向无环图进行拓扑排序所需的时间和V+E成正比。
证明。由代码可知,第一遍深度优先搜索保证了不存在有向环,第二遍深度优先搜索产生了顶点的逆后序排列。两次搜索都访问了所有的顶点和所有的边。因此所需时间和V+E成正比。
5 任务调度方案
在实际应用中 ,拓扑排序和有向环检测总会一起出现,因为有向环检测是拓扑排序的前提。因此,解决任务调度类应用通常需要以下3步:
- 指明任务和优先级;
- 不断检测和去除有向图中的所有环,以确保存在可行方案;
- 使用拓扑排序解决任务调度问题。
类似地,调度方案的任何变动之后都需要再次检测是否存在环,然后再计算新的调度安排。
结语
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p369-377.