力扣刷题

861. 翻转矩阵后的得分

“”"
有一个二维矩阵 A 其中每个元素的值为 0 或 1 。

移动是指选择任一行或列，并转换该行或列中的每一个值：将所有 0 都更改为 1，将所有 1 都更改为 0。

在做出任意次数的移动后，将该矩阵的每一行都按照二进制数来解释，矩阵的得分就是这些数字的总和。

返回尽可能高的分数。

示例：

输入：[[0,0,1,1],[1,0,1,0],[1,1,0,0]]
输出：39
解释：
转换为 [[1,1,1,1],[1,0,0,1],[1,1,1,1]]
0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

提示：

1 <= A.length <= 20
1 <= A[0].length <= 20
A[i][j] 是 0 或 1
思路：
可以这样看，n*m的每个格子都具有一个权重，其中每一行权重都自左向右递减，
为使总和最大则尽可能使权重大的格子填“1”。最左边一列权重最大，所以总可以通过
行翻转使左边第一列全都置“1”，后面就不能再使用行翻转了，以免破环当前的结构，
所以考虑列翻转。对于除最左边第一列外的每一列，总可以通过列翻转使得该列“1”
的个数不小于“0”的个数。最后所有填“1”的格子的权重和即为答案。

“”"
源码

def matrix(A) -> int:
    m, n = len(A), len(A[0])
    for i in range(m):
        if A[i][0] == 0:
            for j in range(n):
                A[i][j] = 1 ^ A[i][j]
    mySum = 0
    #zip(*A)对数组A里的数组进行操作
    for i in zip(*A):
        n -= 1
        mySum += 2** n * max(i.count(1),i.count(0))
    return mySum

1. 两数之和

“”"
给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

“”"
代码

def twoSum(Sums, target):
    hashmap = {}
    for index, num in enumerate(Sums):
        other_num = target - num
        if other_num in hashmap:
            return [hashmap[other_num], index]
        hashmap[num] = index
    
nums = [2, 7, 11, 15]
target = 9
print(twoSum(nums,target))

3. 无重复字符的最长子串

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:

输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:

输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。
示例 4:

输入: s = “”
输出: 0

思路
滑动窗口
代码

i代表最近的字符重复位置 i = max(i, st[S[j]])
ans表示最长的非重复字符串： ans = max(ans, j-i+1)
        j-i+1 ：从当前到最近重复字符的长度
        ans： 记录的最长字符串长度
st[S[j]] = j+1
        ：更新st{}中的字符串

def lengthOfLongest(S: str):
    st = {}
    i, ans = 0, 0
    for j in range(len(S)):
        if S[j] in st:
            i = max(i, st[S[j]])
        ans = max(ans, j-i+1)
        st[S[j]] = j+1
    return ans

s = "abbaffdddftrree"
print(lengthOfLongest(s))

4. 寻找两个正序数组的中位数

题目
给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

def findMed(nums1, nums2):
    nums = nums1 + nums2
    nums.sort()
    Len = len(nums)
    if Len%2 == 0:
        Mode = int(Len/2)
        value = (nums[Mode]+nums[Mode-1])/2.0
    else:
        print(int((Len+1)/2))
        print(nums)
        value = nums[int((Len-1)/2)]
    return value
nums1 = [1,3]
nums2 = [3,4]
print(findMed(nums1, nums2))

7. 整数反转

题目
7. 整数反转

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例 1:

输入: 123
输出: 321
示例 2:

输入: -123
输出: -321
示例 3:

输入: 120
输出: 21

思路：
利用： str.lstrip() 字符串左剔除函数
string = string[::-1] 字符串反转

代码：

def myreverse(x):
    flag = 1
    if x > 2147483647 or x == 0 or x < -2147483647:
        return 0
    elif x < 0:
        flag = -1
        x = -x
    str1 = str(x)
    str1 = str1[::-1]
    str1 = str1.lstrip('0')
    if flag == 0:
        str1 = "-" + str1
    s = int(str1) * flag
    if s > 2147483647 or s < -2147483647:
        return 0
    return s
print(myreverse(334330))

12. 整数转罗马数字

题目
罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。

示例 1:

输入: 3
输出: “III”
示例 2:

输入: 4
输出: “IV”
示例 3:

输入: 9
输出: “IX”
示例 4:

输入: 58
输出: “LVIII”
解释: L = 50, V = 5, III = 3.
示例 5:

输入: 1994
输出: “MCMXCIV”
解释: M = 1000, CM = 900, XC = 90, IV = 4.

代码

# 方法一
def myintToRoman(num):
    list1 = [1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
    list2 = ['M', 'CM', 'D', 'CD', 'C', 'XC', 'L', 'XL', 'X', 'IX', 'V', 'IV', 'I']
    result = ""
    for i in range(len(list1)):
        while num >= list1[i]:
            result += list2[i]
            num -= list1[i]
    return result

print(myintToRoman(800))

# 方法二
def myinToRoman2(num):
    list1 = [1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
    list2 = ['M', 'CM', 'D', 'CD', 'C', 'XC', 'L', 'XL', 'X', 'IX', 'V', 'IV', 'I']
    result = ""
    for i in range(len(list1)):
        if num >=list1[i]:
            result += num//list1[i]*list2[i]
            num = num%list1[i]
    return result

print(myinToRoman2(800))

14. 最长公共前缀

题目

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1:

输入: [“flower”,“flow”,“flight”]
输出: “fl”
示例 2:

输入: [“dog”,“racecar”,“car”]
输出: “”
解释: 输入不存在公共前缀。
说明:

所有输入只包含小写字母 a-z 。

思路：
1、利用python的max()和min()，在Python里字符串是可以比较的，
按照ascII值排，举例abb， aba，abac，最大为abb，最小为aba。
所以只需要比较最大最小的公共前缀就是整个数组的公共前缀

def longestCommonPrefix(strs):
    if not strs: return ""
    s1 = max(strs)
    s2 = min(strs)
    for i,x in enumerate(s1):
        if x != s2[i]:
            return s2[:i]
    return s1
strs = ["flower","flow","flight"]

common = longestCommonPrefix(strs)
print(common)

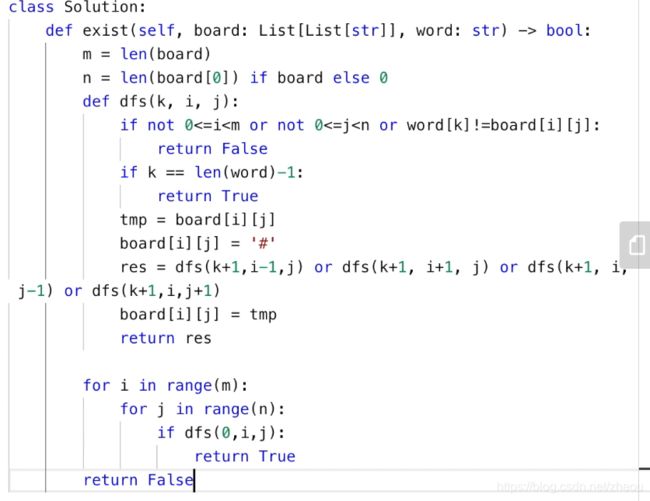
矩阵中的路径

def exist(board, word):
    m = len(board)
    n = len(board[0])
    def dfs(k, i, j):
        if not 0 <= i <m or not 0<=j<n or word[k] != board[i][j]:
            return False
        if k == len(word) -1:
            # print(True)
            return True
        tmp = board[i][j]
        board[i][j] = "#"
        res = dfs(k+1,i,j-1) or dfs(k+1,i+1,j) or dfs(k+1,i,j+1) or dfs(k+1,i-1,j)
        board[i][j] = tmp
        return res
    for i in range(m):
        for j in range(n):
            if dfs(0, i, j):
                return True
    return False




if __name__ == "__main__":
    board = [["A", "B", "C", "C"],
             ["C", "C", "E", "E"],
             ["A", "D", "E", "D"]]
    word = "ABCCED"
    print(exist(board, word))