论文笔记：BPR-Bayesian Personalized Ranking from Implicit Feedback | 推荐系统BPR算法分析

BPR:Bayesian Personalized Ranking from Implicit Feedback

论文链接：BPR:Bayesian Personalized Ranking from Implicit Feedback
会议：UAI2009

转载请声明出处： https://blog.csdn.net/angus_huang_xu/article/details/114499030

1. 背景

物品推荐主要任务是为每个用户创建特定的商品排序，用户对于物品的偏好是根据用户以往的购买记录等信息学习到的。根据获得的用户数据来分类可以将推荐任务分为两类，基于显式反馈的推荐和基于隐式反馈的推荐。

显式反馈一般指的是用户对商品的喜好程度被量化表示，比如豆瓣上用户对电影的打分，分数越高就代表越喜欢。
隐式反馈则是无法量化表示用户对物品喜好程度的数据，比如用户浏览或者点击某商品。

在商品推荐领域常用的方法有矩阵分解（Matrix Factorization）和最近邻搜索（kNN）等。但是这两种方法都没有针对推荐排序问题的优化方法，因此本文提出一个关于针对个性化推荐排序问题的优化方法——BPR-OPT，并将其应用到MF和kNN方法之中。

本文的主要贡献有：

1. 提出了一种基于最大后验估计的优化指标BPR-OPT；
2. 为了最大化BPR-OPT，提出了一种通用的基于带有bootstrap采样的随机梯度下降学习算法LearnBPR；
3. 将LearnBPR算法应用到MF和kNN两种模型中；

2. 问题建模

$U,I$ 分别表示为所有的user和item的集合，隐式反馈 $S\subseteq U\times I$（一般表现为0-1矩阵，即user和item有交互对应位置为1，否则为0）。用 ${>}_u\subset I^2$ 表示用户 $u$ 对物品直接的偏好关系。若 $i{>}_{u}j$ 表示用户 $u$ 更喜欢物品 $i$。
为了方便表示，我们记：

$$\begin{gathered} I_u^{+}=\{i\in I:(u,i)\in S\} \\ {U}_i^{+}=\{u\in U:(u,i)\in S\} \end{gathered}$$

值得一提的是，这种序关系满足三条性质：
$$\begin{array}{lr}\forall i,j\in I:i\ne j\Rightarrow i{>}_{u}j\vee j{>}_{u}i& \text{ (totality) }\\ \forall i,j\in I:i{>}_{u}j\wedge j{>}_{u}i\Rightarrow i=j& \text{ (antisymmetry) }\\ \forall i,j,k\in I:i{>}_{u}j\wedge j{>}_{u}k\Rightarrow i{>}_{u}k& \text{ (transitivity) }\end{array}$$

实际上我们的问题转换成下图所示：已知左侧的矩阵信息，预测出矩阵中未知的信息。

当然，实际情况并不是像图中表示的只需要预测出0-1，一般算出user对item的rating，一般情况分数越高表示偏好程度越高，而后根据此分数来进行排序。

在本文中，解决问题的一个方式是每次优化一个item对，优化的并不是用户对单个item的评分，而是用户对两个item的
偏好关系。有：
$$D_S:=\{(u,i,j)|i\in I_U^{+}\wedge j\in I\backslash I_u^{+}\}$$
那么，$(u,i,j)\in D_S$ 就表示 $u$ 在 $i,j$ 中更喜欢 $i$，此为正样本，那么反过来 $(u,j,i)$ 即为负样本。

这种建模方法有两个优点：

1. 这样处理后data既包含正样本也包含负样本以及缺失信息的样本。比如两个都没有交互的物品之间的序关系就是未知的，是我们要学的；
2. 这样构造的数据是直接为了学习排序的，体现了一种序关系。

3. BPR基本思想

1. BPR-OPT优化指标

   首先根据贝叶斯公式有：
   $$p(\Theta |{>}_u)\propto p({>}_u|\Theta )p(\Theta )$$

   这里，我们有两个基本假设：

    1. 所有user之间的偏好关系是相互独立的
    2. 同一用户对不同物品的偏序相互独立，即我们假设用户对 (i,j) 的偏好是不受其他商品影响的。 
   

   这里我们需要最大化的有两项，第一项跟数据有关，第二项跟模型参数有关。首先我们来看第一项，那么有：

   $$\prod _{u\in U}p({>}_u|\Theta )=\prod _{(u,i,j)\in U\times I\times I}p(i{>}_{u}j|\Theta {)}^{\delta ((u,i,j)\in D_S)}\cdot (1-p(i{>}_{u}j|\Theta ){)}^{\delta ((u,i,j)\notin D_S)}$$
   (注意，原论文中第二个概率上角标有误)
   现在让我们来化简该项，对于每个user，给定商品对 (i,j) ，其关系有四种：

   $\delta ((u,i,j)\in D_S)$	i是正样本	i是未观测的样本
   j是正样本	0	0
   j是未观测的样本	1	0

   根据以上关系，上式可以化简为:
   $$\prod _{u\in U}p({>}_u|\Theta )=\prod _{(u,i,j)\in D_S}p(i{>}_{u}j|\Theta {)}^2$$
   根据概率的非负性，上面式子将平方去掉和原式等价，那么就有论文中的形式：
   $$\prod _{u\in U}p({>}_u|\Theta )=\prod _{(u,i,j)\in D_S}p(i{>}_{u}j|\Theta )$$
   为了最大化上面的式子，我们需要找到一个用来合理表示 $p(i{>}_{u}j|\Theta )$的函数，它需要具有上面讲到的三个性质，论文中选择 sigmoid 函数。即：
   $$p(i{>}_{u}j|\Theta )=\sigma ({\hat{x}}_{uij}(\Theta ))$$
   其中，$\sigma (x)=\frac{1}{1+e^{-x}}$.

   为什么要选择sigmoid函数呢？
   这里个人的理解是因为在这种偏序关系的体现中，用户在正样本和未观测样本之间偏向一个正样本的概率应该很接近1，所以sigmoid作为一个很接近阶跃函数的可导函数很适用。

   ${\hat{x}}_{uij(\Theta )}$为模型对用户u对 i 和 j 相对的打分，视模型而定

   看完贝叶斯公式中对似然函数项的分析后，我们接下来看看对第二项先验分布的优化：

   采用的方法是先假定 $\Theta$ 服从高斯分布，均值为0，方差为协方差矩阵 ${\sum }_{\Theta }$
   $$p(\Theta )\sim N(0,{\sum }_{\Theta })$$

   为了减少参数的数量，令 ${\sum }_{\Theta }={\lambda }_{\Theta }I$，那么原先的优化问题就转换为：
   $$\begin{array}{rl}\text{ BPR-OPT }& :=\ln p\left(\Theta \mid {>}_u\right)\\ & =\ln p\left({>}_u\mid \Theta \right)p(\Theta )\\ & =\ln \prod _{(u,i,j)\in D_S}\sigma \left({\hat{x}}_{uij}\right)p(\Theta )\\ & =\sum _{(u,i,j)\in D_S}\ln \sigma \left({\hat{x}}_{uij}\right)+\ln p(\Theta )\\ & =\sum _{(u,i,j)\in D_S}\ln \sigma \left({\hat{x}}_{uij}\right)-{\lambda }_{\Theta }\Vert \Theta {\Vert }^2\end{array}$$
   其中，${\lambda }_{\Theta }\Vert \Theta {\Vert }^2$ 就是正则化项。

   为什么BPR-OPT和AUC指标类似？

   首先来看些AUC指标：

   通常定义AUC是ROC曲线下的面积，用来衡量模型能不能将用户喜欢的和不喜欢的分辨出来。但是在推荐系统中ROC曲线绘制比较繁琐，一般采用如下近似：
   $$AUC(u):=\frac{1}{|I_u^{+}||I\backslash I_u^{+}|}\sum _{i\in I_u^{+}}\sum _{j\in I\backslash I_u^{+}}\delta ({\hat{x}}_{ij}>0)$$(该公式论文中也写错了，在第二个求和号下标多加了一个集合的势的符号)

   AUC指标对所有用户平均有：
   $$AUC=\frac{1}{|U|}\sum _{u\in U}AUC(u)$$

   利用前面提出的 $D_S$ 的定义，可以改写成：
   $$AUC(u)=\sum _{(u,i,j)\in D_S}{z}_u\delta ({\hat{x}}_{ij}>0),z_u=\frac{1}{|U||I_u^{+}||I\backslash I_u^{+}|}$$

   BPR-OPT和AUC的相似性显然可以看出来，区别在于AUC指标里面用的 $\delta$ 函数通常是阶跃函数，不可导；而在BPR-OPT中改用 $\sigma$ 函数，是通常用来代替阶跃函数的一种可导的函数。

2. BPR算法
   根据上面提出的BPR-OPT指标，我们采用梯度下降的算法。对BPR-OPT指标求导：
   $$\begin{array}{rl}\frac{\partial \mathrm{B}\mathrm{P}\mathrm{R}-\mathrm{O}\mathrm{P}\mathrm{T}}{\partial \Theta }& =\sum _{(u,i,j)\in D_S}\frac{\partial }{\partial \Theta }\ln \sigma \left({\hat{x}}_{uij}\right)-{\lambda }_{\Theta }\frac{\partial }{\partial \Theta }\Vert \Theta {\Vert }^2\\ & \propto \sum _{(u,i,j)\in D_S}\frac{-e^{-{\hat{x}}_{uij}}}{1+e^{-{\hat{x}}_{uij}}}\cdot \frac{\partial }{\partial \Theta }{\hat{x}}_{uij}-{\lambda }_{\Theta }\Theta \end{array}$$
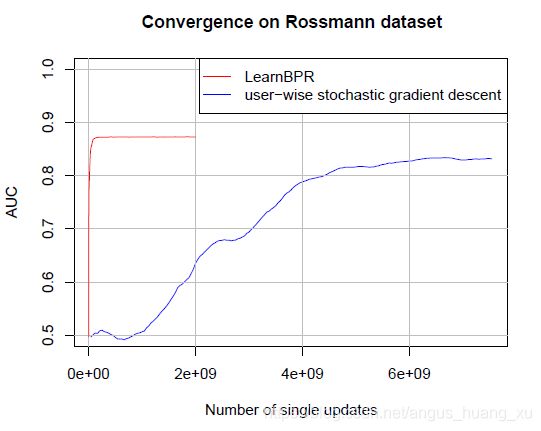
   算法流程如下：

   1: LearnBPR 算法
   2: 	初始化 Θ
   3: 	循环直至收敛：
   4: 		从 Ds 中取出 （u,i,j）
   5: 		利用梯度下降更新 Θ
   6: 	返回模型参数 Θ
   

   针对该算法还需要考虑的一个问题是使用哪种梯度下降算法，完全梯度下降还是随机梯度下降。

   1. 完全梯度下降
      完全梯度下降每次需要对所有的(u,i,j)三元组进行计算梯度，带来的问题其一是每次计算量太大，在推荐任务中用户数和商品数望望都是十分大的，一次性计算所有三元组的梯度不太现实；其二是对于每一个用户，通常只有少部分交互过的商品，大部分商品都是没有交互的，因此对于每一个i，会有很多j 来组成pair，商品 i 在梯度中就占了主导地位，这种倾斜也会带来收敛速度慢。
   2. 随机梯度下降
      随机梯度下降是每次计算梯度只选择一个（u,i,j）三元组进行计算，但是需要考虑的问题是以什么顺序遍历所有的三元组，如何选择。常见的顺序都是 item-wise或者 user-wise，但是由于推荐中数据的稀疏性，都会带来倾斜，和上面完全梯度下降有同样的问题。在本文中，提出了的解决方法也很简单，使用随机选择的策略选择用于计算的三元组。

   文中给出了user-wise的随机梯度下降和本文随机选择策略的随机梯度下降算法收敛性的差别：
   

4. 算法中的应用

本文给出了LearnBPR算法在两个常见的推荐的模型MF（Matrix Factorization）和kNN（k Nearest Neighbor）中的应用。由于在这两种模型中，输出的都是用户u对商品i的打分 ${\hat{x}}_{ui}$，和BPR算法需要的item pair不一样，所以定义：
$${\hat{x}}_{uij}={\hat{x}}_{ui}-{\hat{x}}_{uj}$$

1. MF(Matrix Factorization)
   矩阵分解的思想就是将数据中得到的 rating矩阵 $X\in \{0,1{\}}^{|U|\times |I|}$ 拆解成两个矩阵 $W:|U|\times k$和$H:|I|\times k$，分别代表user矩阵和item矩阵，将模型的预测定义为：
   $$\begin{gathered} \hat{X}:=W{H}^T \\ {\hat{x}}_{ui}=⟨w_u,h_i⟩=\sum _{f=1}^k{w}_{uf}\cdot h_{if} \end{gathered}$$
   那么目标就变成了优化 $X$ 和 $\hat{X}$ 之间的距离，常用的MF方法有 SVD-MF, WR-MF.

   • SVD-MF:
     基本思想是利用奇异值分解将X矩阵分解为W和H矩阵，详见博客 【SVD在推荐系统中的应用详解以及算法推导】
   • WR-MF(Weighted Regularized Matrix Factorization):
     本质上也是基于SVD，但是对loss函数进行优化，形式为：
     $$\sum _{u\in U}\sum _{i\in I}{c}_{ui}{\left(⟨w_u,h_i⟩-1\right)}^2+\lambda \Vert W{\Vert }_f^2+\lambda \Vert H{\Vert }_f^2$$
     其中， $c_{ui}$ 不是模型参数，是相关权重，基于人为预先设定的。

   在BPR-OPT指标中，我们需要的导数关系：
   $$\frac{\partial }{\partial \theta }{\hat{x}}_{uij}=\{\begin{array}{ll}\left(h_{if}-h_{jf}\right)& \text{ if }\theta =w_{uf},\\ w_{uf}& \text{ if }\theta =h_{if}\\ -w_{uf}& \text{ if }\theta =h_{jf}\\ 0& \text{ else }\end{array}$$
   对于正则化系数，设置有3个：${\lambda }_W,{\lambda }_{H^{+}},{\lambda }_{H^{-}}$，分别用于对W和正负样本的H做正则。

2. Adaptive k-Nearest-Neighbor
   k近邻搜索是传统协同过滤算法中最常用的一种，它是一种基于用户相似度或者物品相似度度量后选择k个最近邻的物品进行推荐的。简单的以基于物品的来说，对于一个用户，以他的历史记录作为参考，选择k个距离其历史记录中的商品最近的商品作为其推荐。

   其中，有：
   $${\hat{x}}_{ui}=\sum _{l\in I_u^{+}\wedge l\ne i}{c}_{il}$$
   其中，$c_{il}$是商品与商品之间的距离度量矩阵，也就是模型的参数。导数关系如下：
   $$\frac{\partial }{\partial \theta }{\hat{x}}_{uij}=\{\begin{array}{ll}+1& \text{ if }\theta \in \left\{c_{il},c_{li}\right\}\wedge l\in I_u^{+}\wedge l\ne i\\ -1& \text{ if }\theta \in \left\{c_{jl},c_{lj}\right\}\wedge l\in I_u^{+}\wedge l\ne j\\ 0& \text{ else }\end{array}$$

5. 实验结果

文章在两个数据集上进行AUC指标的评估，结果如下图：