贝叶斯自举法(BayesianBootstrap)简介
本文有目录
- 自举法Bootstrap分类
- 频率派自举法
- 贝叶斯自举法
-
- 为什么贝叶斯自举法
- 贝叶斯自举法的工作原理
- 参考文献
自举法Bootstrap分类
在对数据的统计分析时,一般首先假设参数形式的概率密度分布。但是如果我们的统计模型对这个预先假设很敏感,那么如何决定假设的内容就很重要了。避免对数据特征的事先假设似乎可以解决上述问题,事实上它也一直是一个重要课题。
确定模型的不确定区间可以很好地评价我们模型的可靠度,同时也可以告诉我们模型不知道的范围。自举法概念清晰,执行简单,是一种很好地非参数方法。
按照频率派和贝叶斯派的范畴,自举法Bootstrap可分为频率派自举法(经典自举法)和贝叶斯自举法。
频率派自举法
频率派自举法的一些介绍可参照我的博文。但为了与贝叶斯自举法比较,在此仍罗列一些概念。
假设:将Bootstrap采样得到的数据等价为未知总体分布的合理近似。
记 y = ( y 1 , … , y n ) y= (y_1,\ldots,y_n) y=(y1,…,yn)为样本容量为n的观测值,那么随机抽样(可放回)可以得到一组抽样序列 y b = ( y 1 b , … , y n b ) y^b = (y_1^b, \ldots, y_n^b) yb=(y1b,…,ynb)。则抽样序列的均值 m b m_b mb为
m b = 1 n ∑ i = 1 n y i b (1) m_b = \frac{1}{n} \sum_{i=1}^n y_i^b\tag{1} mb=n1i=1∑nyib(1)
当重复抽样,我们可以得到足够多的 m b m_b mb,并假设其分布为 m b m_b mb的总体分布。
注意 y b y^b yb中的元素是 y y y元素的子集,也就是说,可放回抽样的操作使得 y b y^b yb中的元素频率不一(相对 y y y)。
贝叶斯自举法
为什么贝叶斯自举法
在频率派自举法中,如果数据样本很稀缺,那么我们采样得到的概率密度分布就会不够光滑,如下图a所示,而贝叶斯自举法可以得到图b的效果。
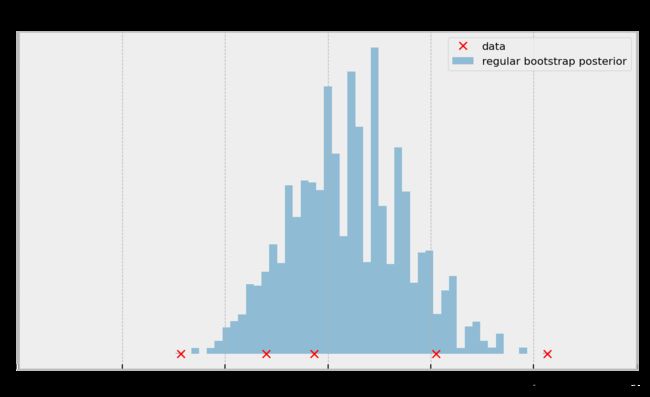 (a) 频率派自举法 (a) 频率派自举法
|
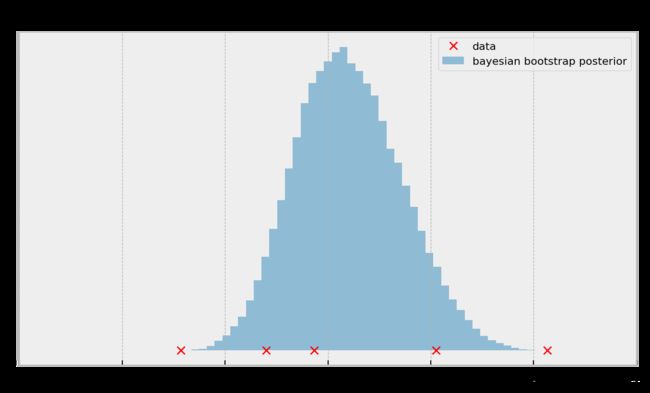 (b) 贝叶斯自举法 (b) 贝叶斯自举法
|
贝叶斯自举法的工作原理
接公式(1),在 y b = ( y 1 , … , y b ) y^b= (y^1,\ldots,y^b) yb=(y1,…,yb)中重复元素 y i y_i yi的频数为 h b = ( h 1 b , … , h n b ) h^b = (h_1^b, \ldots, h_n^b) hb=(h1b,…,hnb),那么 h b h^b hb满足 h i b ∈ { 0 , 1 , … , n − 1 , n } h_i^b \in \{0, 1, \ldots, n-1,n\} hib∈{0,1,…,n−1,n}且 ∑ i = 1 n h i b = n \sum\limits_{i=1}^n h_i^b = n i=1∑nhib=n。对 h b h^b hb所有元素除以 n n n可以得到权重序列 w i b = h i b / n = ( h 1 b , … , h n b ) / n w_i^b = h_i^b/n= (h_1^b, \ldots, h_n^b)/n wib=hib/n=(h1b,…,hnb)/n。公式(1)就可以替换为下式,
m b = ∑ i = 1 n w i b y i (2) m_b = \sum_{i=1}^n w_i^b\, y_i\tag{2} mb=i=1∑nwibyi(2)
对于频率派来说,如何抽样 y i y_i yi(都对应一组 w b w^b wb和 y i y_i yi)决定了 m b m_b mb;对于贝叶斯派来说,我们理解为 y y y固定不变,而是其权重为概率分布。
具体来说,对于频率派 h b h^b hb满足多项式分布,也就是公式(3)所示,
h b = ( n w b ) ∼ Multinomial ( n , ( 1 / n ) i = 1 n ) (3) h^b=(n\,w^b) \sim \textsf{Multinomial}(n,(1/n)_{i=1}^n)\tag{3} hb=(nwb)∼Multinomial(n,(1/n)i=1n)(3)
对于贝叶斯派来说,我们认为 y y y固定不变,它的参数 w i w_i wi符合某一种参数分布(公式(4))。而每次采样都产生一个后验分布,在此过程中未被采样到的 y i y_i yi概率密度设为0。
μ = ∑ i = 1 n w i y i (4) \mu = \sum_{i=1}^n w_i\, y_i\tag{4} μ=i=1∑nwiyi(4)
其中后验分布 w i w_i wi满足Dirichlet distribution(公式(5))【1,8】,这也是为什么图(a-b)中光滑程度不一致的原因,狄利克雷分布要比多项式分布更平滑。
w ∼ Dirichlet ( 1 , … , 1 ) (5) w \sim \textsf{Dirichlet}(1,\ldots,1) \tag{5} w∼Dirichlet(1,…,1)(5)
令人好奇的是先验分布在哪里呢? 答案是数据是离散的Dirichlet分布,在数据中不存在取不到的值。
自举法,包括频率派自举法和贝叶斯自举法并不是完美的,它们的一些适用范围仍然是有待验证的,他们可能非常合理也可能非常不合理,感兴趣的读者可参照【7】,本文不再赘述。但要记住的是两种方法的结果理论上都是等效的。
【9】
且用工而后已者,必用工而后已。
参考文献
【1】Rubin, & Donald, B. . (1981). The bayesian bootstrap. Annals of Statistics, 9(1), 130-134.
【2】Python实现
【3】R语言实现
【4】https://stats.stackexchange.com/questions/181350/bootstrapping-vs-bayesian-bootstrapping-conceptually
【5】https://gdmarmerola.github.io/the-bayesian-bootstrap/
【6】http://www.sumsar.net/blog/2015/04/the-non-parametric-bootstrap-as-a-bayesian-model/
【7】https://rgiordan.github.io/bayesian_bootstrap/2019/08/11/bayesian_bootstrap.html
【8】Dirichlet distribution简介–张天蓉老师
【9】 Cirillo, P. , & Muliere, P. . (2013). An urn-based bayesian block bootstrap. Metrika, 76(1), 93-106.