PyTorch|自动求导系统AutoGrad
01 | PyTorch的自动求导系统AutoGrad
从前述课程中,我们已经知道:PyTorch训练机器学习或深度学习模型时,依赖于计算优化目标函数(如Loss函数)时的反向传播梯度,并以此层层求导更新每个计算图中结点的数值(权重)。
然而,深度学习架构中经常面临成百上千的待确定参数,而这意味着需要对几百个参数进行导数运算,对于人工而言无疑是困难且低效的。
PyTorch为此提供了自动求导系统AutoGrad,只需要我们根据模型动态搭建好正向计算图,继而调用AutoGrad系统提供“backward”方法以实现模型训练过程。
AutoGrad中最常用的方法是**“torch.autograd.backward()**”,其作用就是自动求取计算图中各个结点的梯度,主要参数有四个:
-
tensors:表示用于求导的张量,如常用的目标Loss函数
-
retain_graph:标记是否要保留计算图,默认情况下一次反向传播结束后,即销毁计算图以节省内存空间
-
create_graph:创建导数的计算图,尤其用于高阶求导(如二阶偏导数)
-
grad_tensors:多梯度权重,用于在多维目标训练时指定,以计算最终的梯度
02 | Backward()使用介绍
为了进一步说明AutoGrad机制,这里我们再次使用之前课程中的示例:
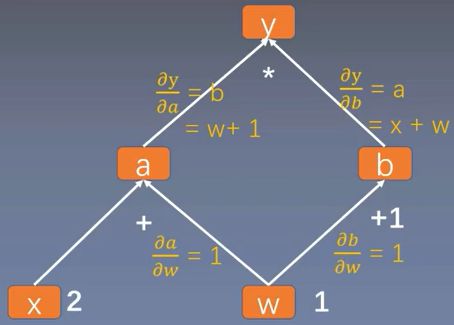
y = ( x + w ) × ( w + 1 ) y = (x + w) \times (w + 1) y=(x+w)×(w+1)
其针对w的求导公式为:
∂ y ∂ w = ∂ y ∂ a ∂ a ∂ x + ∂ y ∂ b ∂ b ∂ w \frac{\partial y}{\partial w}=\frac{\partial y}{\partial a}\frac{\partial a}{\partial x} + \frac{\partial y}{\partial b}\frac{\partial b}{\partial w} ∂w∂y=∂a∂y∂x∂a+∂b∂y∂w∂b
类似地,可以绘制出其正向传播的计算图:
021 | retain_graph参数
我们先来看一个规范的AutoGrad应用,具体代码如下。其中backward()实质上调用了**torch.autograd()**方法。
import torch
torch.manual_seed(10)
# retain_graph
flag = True if flag:
# 创建叶子结点
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# 设置正向计算公式
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
# 执行反向传播算法计算梯度
y.backward(retain_graph=True) # retain_graph默认为False
print(w.grad)
y.backward(retain_graph=True)
print(w.grad)
y.backward(retain_graph=True)
print(w.grad)
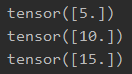
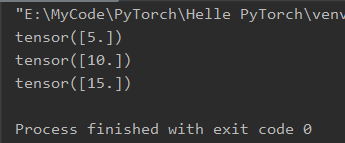
其中求解目标函数y相对于自变量w的梯度值,可以看到其结果为“5”;随后我们执行了第二次梯度运算,发现其结果为“10”,这里有两点需要注意:1)若想连续对某个张量求梯度,则必须设置“retain_graph=True”,否则一旦计算图随着第一次求解梯度后动态消失,则无法基于该图执行第二次计算;2)若不对梯度进行特殊处理,连续多次求解梯度,可以发现其值是多次结果的叠加(5→10→15)。
022 | grad_tensors参数
我们在PyCharm中设置y0=a×b和y1=a+b两个目标函数,并将二者的拼接作为新的目标函数,即Loss=[y0, y1]。此时计算Loss相对于w的梯度时,就可以根据设定的grad_tensors中的权重参数,分别加权求得最终的梯度。
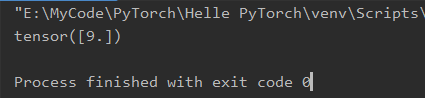
在运行代码前,我们可以试着分析下,对于y0而言,其在w处梯度为5;而y1在w处的偏导数为常数2,因而其梯度值也为2;但是由于grad_sensors中指定的权重张量为[1., 2.],因此实际求解的loss在w处的梯度值为(5 + 2×2 = 9),运行代码可以验证上述分析。
flag = True
if flag:
# 创建叶子结点
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# 设置正向计算公式
a = torch.add(w, x)
b = torch.add(w, 1)
# 设置两个目标函数
y0 = torch.mul(a, b)
y1 = torch.add(a, b)
# 新的损失函数
loss = torch.cat([y0, y1], dim=0)
grad_tensors = torch.tensor([1., 2.])
# 设定不同张量对应的权重
# 针对loss函数求解梯度时需要考虑权重
loss.backward(gradient=grad_tensors)
print(w.grad)
03 | torch.autograd.grad
上面所讲的torch.autograd.backward()默认仅计算了叶子结点的梯度,如果想知道任意结点的梯度该怎么办呢?我们可以使用“torch.autograd.grad()”。
该方法的功能就是求取梯度,其主要参数有五个:
-
outputs:表示用于求导的张量,如loss函数
-
inputs:表示需要梯度的张量
-
create_graph:创建导数的计算图,用于高阶求导
-
retain_graph:保存计算图
-
grad_outputs:多梯度权重
按照惯例,我们采用PyCharm进行代码演示如何借助该方法求解二阶导数。
flag = True
if flag:
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)
# 计算打印1阶导数
grad_1 = torch.autograd.grad(y, x, create_graph=True)
print(grad_1)
# 计算打印2阶导数
grad_2 = torch.autograd.grad(grad_1[0], x)
print(grad_2)
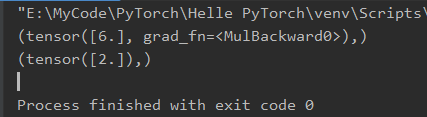
上述代码执行过程中,“grad_1”表示函数y=x^2的一阶导数,其必须设置参数“create_graph=True”创建导数的计算图,才可以对导数进行进一步求导。
在求解“grad_2”时,需要注意其输入参数“outputs”应该是上步所求得的一阶导数,而由于其为一个张量,因此需要采用索引[0]选择出该元素,后续类似。
若想继续求解导数的导数,则上一次求导过程务必创建导数的计算图。
最终结果中,y=x^2的一阶导数是2x,二阶导数是常数2,代入x=3,可知结果正确。
04 | AutoGrad需要注意的问题
总体而言,AutoGrad的使用并不复杂,但是有几点需要注意:
-
AutoGrad计算中梯度不会自动清零
-
依赖于叶子结点的结点,requires_grad默认都为True;这点从计算图上看是显然的,如本例中结点a依赖于叶子节点w和x,反之w和x的梯度计算依赖于a的梯度,因而结点a的必须设定为要求计算梯度,即requires_grad=True。
-
叶子节点不可执行in-place操作
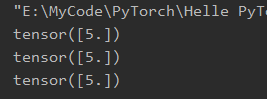
在*[021]*小节中,我们已经看到了连续多次计算某个结点梯度时,出现梯度值叠加的情况,因为在一次迭代中,对该结点的梯度计算使用相同的计算图,因而其梯度值是相同值的叠加。这个时候我们只需要在计算求解梯度w.grad()后,运行**w.grad.zero_()**主动清零即可。
不信请看下述修改后的代码,修改添加前期结果为正常叠加,修改后可以正确计算梯度。
flag = True
if flag:
# 创建叶子结点
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
for i in range(3):
# 设置正向计算公式
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
# 执行反向传播算法计算梯度
y.backward()
print(w.grad)
# 每次计算后对w的梯度人工清零
w.grad.zero_()
in-place可以理解为“原位操作”或“原地址操作”,即在原始内存位置直接修改数据。如在PyCharm中执行下述代码,可以看出,当执行“a = a + Tensor”的时候,左右变量a的内存地址发生了变化,即创建了新变量;而当采用“a += Tensor”时,可以看出前后变量a的内存地址一致,即在原始内存位置进行了数据改变,称之为“in-place”。
之所以叶子结点不允许执行“in-place”操作,其原因依旧可从计算图上略窥一斑。即前向传播时,PyTorch记录了叶子结点的内存地址,以便于后向传播时随时调用叶子结点的数值计算出相应的偏导数。若在此过程中允许叶子结点“in-place”操作,势必导致其出现数值计算错误。
flag = True
if flag:
a = torch.ones((1,))
print(id(a), a)
a = a + torch.ones((1, ))
print(id(a), a)
a += torch.ones((1, ))
print(id(a), a)