计算机组成原理机器码怎么求,计算机组成原理--数据格式与机器码
数据格式
计算机中使用的数据可分成两大类:
符号数据:非数字符号的表示(ASCII、汉字、图形等)
数值数据:数字数据的表示方式(定点、浮点)
计算机数字和字符的表示方法应有利于数据的存储、加工(处理)、传送;
编码:用少量、简单的基本符号,选择合适的规则表示尽量多的信息,同时利于信息处理(速度、方便)
进制转换
这个一般都不是问题,但二进制小数转十进制我忘了,所以在这复习一下
例如将0.11101转为十进制那么应该这样做:0*2^(0)+ 1*2^(-1)+1*2^(-2)+1*2^(-3)+ 0*2^(-4)+1*2^(-5)
计算机在数据、文字的表示方式时,应该考虑一下几个因素:
表示的数据类型(符号、小数点、数值)
数值的范围
数值精度
存储、处理、传送的硬件代价
是否有利于软件的移植等...
定点表示
所有数据的小数点位置固定不变,理论上位置可以任意,但实际上将数据表示有两种方法(小数点位置固定-定点表示法/定点格式):纯小数和纯整数,然后又分带符号不带符号
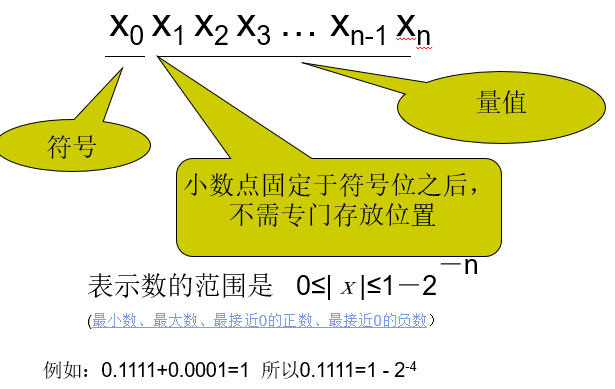
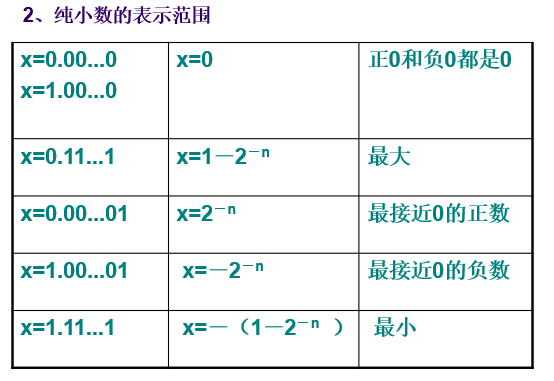
定点纯小数
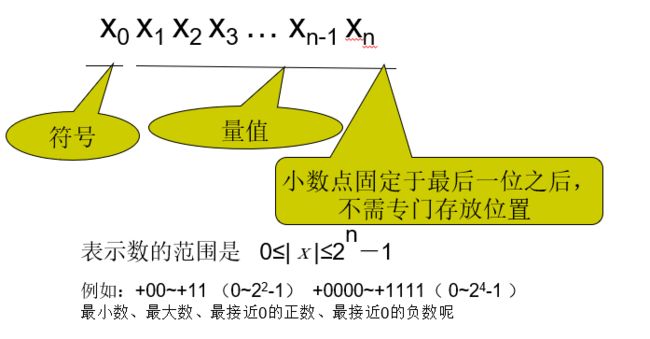
定点纯整数
定点表示法的特点:
定点数表示数的范围受字长限制,表示数的范围有限;
定点表示的精度有限
机器中,常用定点纯整数表示;
因为要表示实数(包括小数和整数),所以引入浮点数
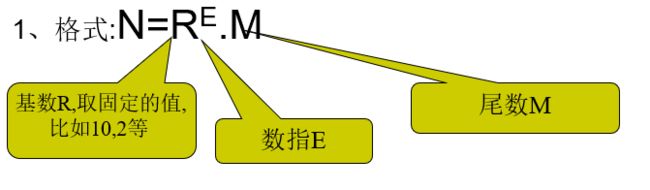
浮点表示:小数点位置随阶码不同而浮动
机器中表示
IEEE754标准(规定了浮点数的表示格式,运算规则等)规则规定了单精度(32)和双精度(64)的基本格式,规则中,尾数用原码,指数用移码(便于对阶和比较)
IEEE754标准
基数R=2,基数固定,采用隐含方式来表示它。
32位的浮点数:
S数的符号位,1位,在最高位,“0”表示正数,“1”表示负数。
M是尾数, 23位,在低位部分,采用纯小数表示
E是阶码,8位,采用移码表示。移码比较大小方便。
规格化: 若不对浮点数的表示作出明确规定,同一个浮点数的表示就不是惟一的。
尾数域最左位(最高有效位)总是1, 故这一位经常不予存储,而认为隐藏在小数点的左边
采用这种方式时,将浮点数的指数真值e变成阶码E时,应将指数e加上一个固定的偏移值127(01111111),即E=e+127
E: 阶码位数,决定数据的范围,M: 尾数位数,决定数的精度
真值x为零表示:当阶码E为全0且尾数M也为全0时的值,结合符号位S为0或1,有正零和负零之分
真值x为无穷大表示:当阶码E为全1且尾数M为全0时,结合符号位S为0或1,也有+∞和-∞之分。
这样在32位浮点数表示中,要除去E用全0和全1(255)表示零和无穷大的特殊情况,指数的偏移值不选128(10000000),而选127(01111111)。对于规格化浮点数,E的范围变为1到254,真正的指数值e则为-126到+127。因此32位浮点数表示的绝对值的范围是10-38~1038(以10的幂表示)。
浮点数所表示的范围远比定点数大。一台计算机中究竟采用定点表示还是浮点表示,要根据计算机的使用条件来确定。一般在高档微机以上的计算机中同时采用定点、浮点表示,由使用者进行选择。而单片机中多采用定点表示
指数采用偏移值,其中单精度偏移值为127,双精度为1023,将浮点数的阶码值变成非负整数,便于浮点数的比较和排序
机器数的特点
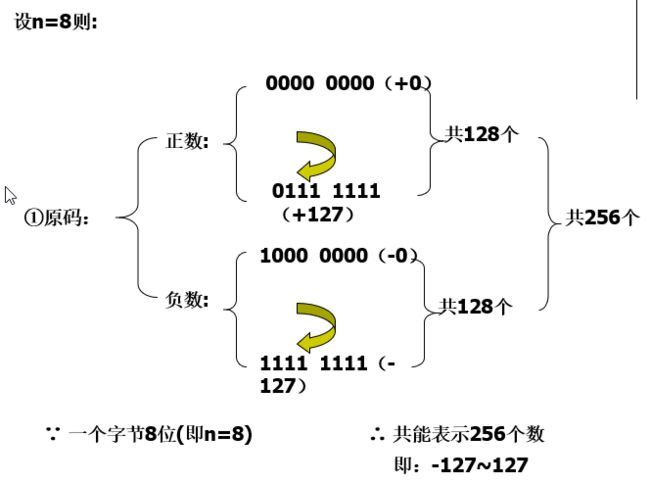
原码:表示简单,运算复杂:符号位不参加运算,要设置加法、减法器,0的表示不唯一,不能直接判定是执行加法还是减法运算,分同号和异号
反码:表示相对原码复杂,运算相对原码简单:符号位参加运算, 只需要设置加法器,但符号位的进位位需要加到最低位,0的表示不唯一
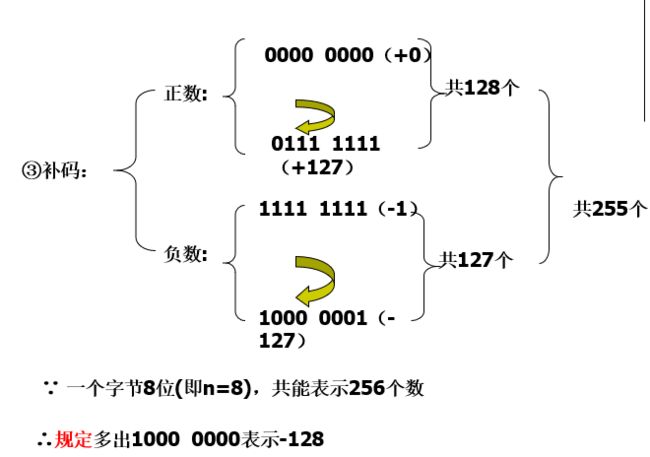
补码:表示相对原码复杂,运算简单:只需设置加法器,0的表示唯一
移码(增码):
BCD码
表示一位十进制数的二进制码的每一位有确定的权。一般用8421码,其4个二进制码的权从高到低分别为8、4、2和1。用0000,0001,…,1001分别表示0,1,…,9,每个数位内部满足二进制规则,而数位之间满足十进制规则,故称这种编码为“以二进制编码的十进制(binary coded decimal,简称BCD)码”
在计算机内部实现BCD码算术运算,要对运算结果进行修正,对加法运算的修正规则是:
如果两个一位BCD码相加之和小于或等于(1001),即(9),不需要修正;如相加之和大于或等于(10),要进行加6修正,并向高位进位,进位可以在首次相加(例3.10③)或修正时产生
码值转换
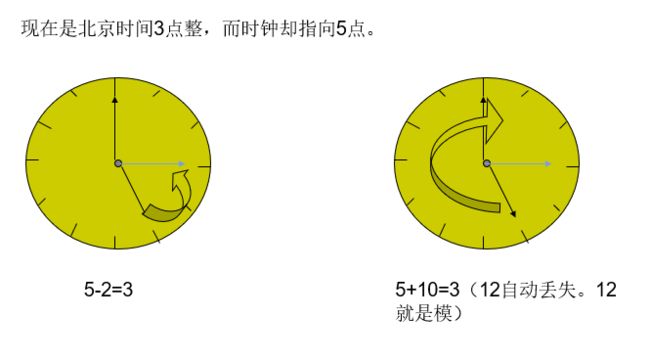
补码是在“模”和“同余”的概念下导出的。
“模”是指一个计量系统的计量范围,即产生“溢出”的量。
5-2=5+10 (MOD 12)
5+(-2)=5+10 (MOD 12)
-2=10 (MOD 12)
可以说:在模为12的情况下,-2的补码 就是10。 一个负数用其补码代替,同样可以得到正确的运算结果。
1、一个负数可用它的正补数来代替,而这个正数可以用模加上负数本身求得。
2、一个正数和一个负数互为补数时,它们绝对值之和即为模数。
进一步结论:
在计算机中,机器能表示的数据位数是一定的,其运算都是有模运算。如果是n位整数(不含符号位),其模为2n+1。如果是n位小数,其模为2。
若运算结果超出了计算机所能表示的数值范围,则只保留它的小于模的低n位的数值,超过n位的高位部分就自动舍弃了。
补码性质:高位表明正负,正数补码,尾数与原码相同,范围-2n~2n-1(定点整数)
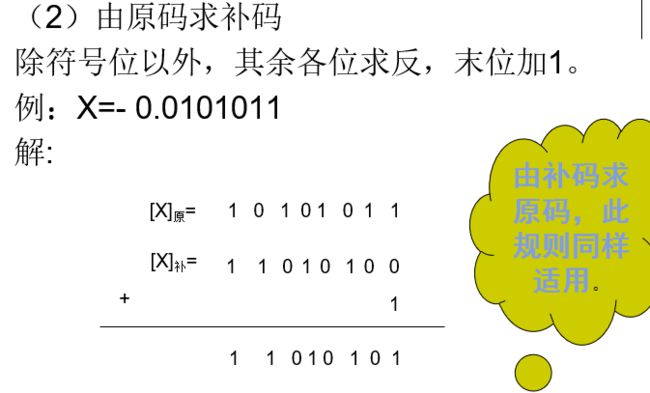
由原码求补码的简便原则:除符号位以外,其余各位按位取反,从最低位开始遇到的第一个1及右边的各位保持不变
由[X]补求[-X]补:连符号位一起各位求反,末位加1。
由[X]补求[X/2]补:将[X]补的符号位和数值位一起向右移动一次.符号位移走后保持原来的值不变.这称为“算术移位”,[X/4]补和[X/8]补同理
n+1位补码所能表示的数
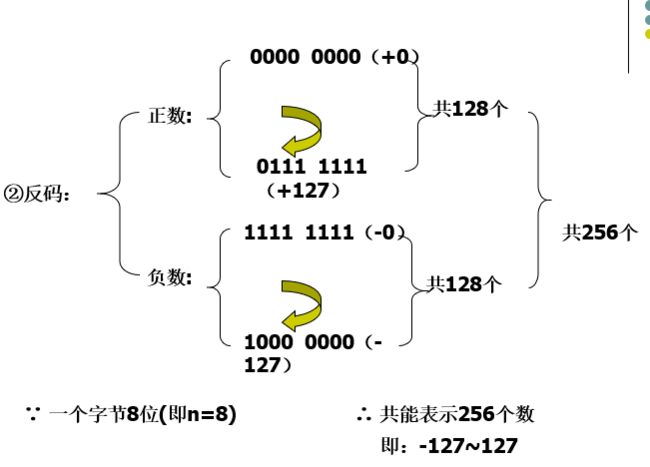
反码表示法
定义:正数的表示与原、补码相同,负数的反码符号位为1,数值位是将原码的数值按位取反,就得到该数的反码表示,电路容易实现,触发器的输出有正负之分
[x ]补=[x ]反+2^-n,反码表示有正0和负0之分
移码
特点:移码和补码尾数相同,符号位相反,范围:-2n~2n-1
性质: 若[X1]移>[X2]移,则有 X1>X2.
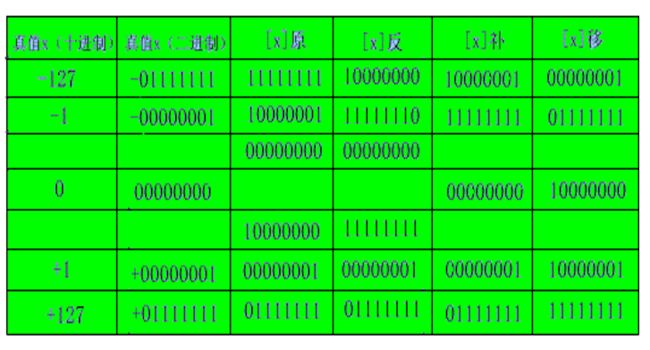
原码、补码、反码和移码的区别,可分三个区域: