hdu 3360 National Treasures
Problem Description
The great hall of the national museum has been robbed few times recently. Everyone is now worried about the security of the treasures on display. To help secure the hall, the museum contracted with a private security company to provide additional guards to stay in the great hall and keep an eye on the ancient artifacts. The museum would like to hire the minimum number of additional guards so that the great hall is secured.
The great hall is represented as a two dimensional grid of R × C cells. Some cells are already occupied with the museum’s guards. All remaining cells are occupied by artifacts of different types (statues, sculptures, . . . etc.) which can be replaced by new hired guards. For each artifact, few other cells in the hall are identified as critical points of the artifact depending on the artifact value, type of vault it is kept inside, and few other factors. In other words, if this artifact is going to stay in the hall then all of its critical points must have guards standing on them. A guard standing in a critical position of multiple artifacts can keep an eye on them all. A guard, however,
can not stand in a cell which contains an artifact (instead, you may remove the artifact to allow the guard to stay there). Also you can not remove an artifact and leave the space free (you can only replace an artifact with a new hired guard).
Surveying all the artifacts in the great hall you figured out that the critical points of any artifact (marked by a ) are always a subset of the 12 neighboring cells as shown in the grid below.
) are always a subset of the 12 neighboring cells as shown in the grid below.
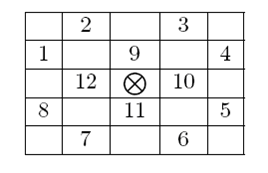
Accordingly, the type of an artifact can be specified as a non-negative integer where the i-th bit is 1 only if critical point number i from the picture above is a critical point of that artifact. For example an artifact of type 595 (in binary 1001010011) can be pictured as shown in the figure below. Note that bits are numbered from right to left (the right-most bit is bit number 1.) If a critical point of an artifact lies outside the hall grid then it is considered secure.

You are given the layout of the great hall and are asked to find the minimum number of additional guards to hire such that all remaining artifacts are secured.
The great hall is represented as a two dimensional grid of R × C cells. Some cells are already occupied with the museum’s guards. All remaining cells are occupied by artifacts of different types (statues, sculptures, . . . etc.) which can be replaced by new hired guards. For each artifact, few other cells in the hall are identified as critical points of the artifact depending on the artifact value, type of vault it is kept inside, and few other factors. In other words, if this artifact is going to stay in the hall then all of its critical points must have guards standing on them. A guard standing in a critical position of multiple artifacts can keep an eye on them all. A guard, however,
can not stand in a cell which contains an artifact (instead, you may remove the artifact to allow the guard to stay there). Also you can not remove an artifact and leave the space free (you can only replace an artifact with a new hired guard).
Surveying all the artifacts in the great hall you figured out that the critical points of any artifact (marked by a
 ) are always a subset of the 12 neighboring cells as shown in the grid below.
) are always a subset of the 12 neighboring cells as shown in the grid below.

Accordingly, the type of an artifact can be specified as a non-negative integer where the i-th bit is 1 only if critical point number i from the picture above is a critical point of that artifact. For example an artifact of type 595 (in binary 1001010011) can be pictured as shown in the figure below. Note that bits are numbered from right to left (the right-most bit is bit number 1.) If a critical point of an artifact lies outside the hall grid then it is considered secure.

You are given the layout of the great hall and are asked to find the minimum number of additional guards to hire such that all remaining artifacts are secured.
Input
Your program will be tested on one or more test cases. Each test case is specified using R+1 lines.
The first line specifies two integers (1<= R,C <= 50) which are the dimensions of the museum hall. The next R lines contain C integers separated by one or more spaces. The j-th integer of the i-th row is -1 if cell (i, j) already contains one of the museum’s guards, otherwise it contains an integer (0 <= T <= 2 12) representing the type of the artifact in that cell.
The last line of the input file has two zeros.
The first line specifies two integers (1<= R,C <= 50) which are the dimensions of the museum hall. The next R lines contain C integers separated by one or more spaces. The j-th integer of the i-th row is -1 if cell (i, j) already contains one of the museum’s guards, otherwise it contains an integer (0 <= T <= 2 12) representing the type of the artifact in that cell.
The last line of the input file has two zeros.
Output
For each test case, print the following line:
k. G
Where k is the test case number (starting at one,) and G is the minimum number of additional guards to hire such that all remaining artifacts are secured.
//二维平面可以分为 坐标和 为奇数和偶数的点 ,而且只有奇偶点才有可能连边 -----以上思路来自百度上他人博客
//这样思路就比较清晰了、 根据输入数据在两个部分连接边 由于每条边都必须必覆盖,而且选的点尽可能下、、于是该题就是求二分图最小点覆盖 ( = 最大匹配 )
// 由于 求点的编号时 (i-1)*C+j 错写成了 (i-1)*R+j Wa了好多次、、纠结一晚上、、郁闷了、、、
//一些细节优化没写了、、刘老师说应该把精力放在问题求解上、、感觉很对
#include <iostream> #include <stdio.h> #include <algorithm> #include <vector> #include <queue> #include <stack> #include <string.h> using namespace std; const int N=2510; bool visit[N]; int match[N]; vector <int> G[N]; int dx[12]={-1,-2,-2,-1,1,2, 2, 1,-1,0,1, 0}; int dy[12]={-2,-1, 1, 2,2,1,-1,-2, 0,1,0,-1}; int R,C; int map[60][60]; bool place(int x,int y) { if(x>=1&&y>=1&&x<=R&&y<=C) return true; return false; } bool dfs(int u) { int i,v; for(i=0;i<G[u].size();i++) { v=G[u][i]; if(!visit[v]) { visit[v]=true; if(!match[v]||dfs(match[v])) { match[v]=u; return true; } } } return false; } int main() { int k=1; while(scanf("%d %d",&R,&C),R|C) { int i,j; int s,t; for(i=1;i<=R;i++) for(j=1;j<=C;j++) scanf("%d",&map[i][j]); for(i=1;i<=R;i++) for(j=1;j<=C;j++) { int w=0,temp=map[i][j]; while(temp>0) { if(temp&1) { s=i+dx[w]; t=j+dy[w]; if(place(s,t)&&map[s][t]>=0) { if((i+j)%2) G[(i-1)*C+j].push_back((s-1)*C+t); else G[(s-1)*C+t].push_back((i-1)*C+j); } } temp=temp>>1; w++; } } memset(match,0,sizeof(match)); int ans=0; for(i=1;i<=R;i++) for(j=1;j<=C;j++) { if((i+j)%2) { memset(visit,0,sizeof(visit)); if(dfs( (i-1)*C+j )) ans++; } } printf("%d. %d\n",k++,ans); for(i=1;i<=R;i++) for(j=1;j<=C;j++) { if((i+j)%2) G[(i-1)*C+j].clear(); } } return 0; }