dfs与逆序对结合（概率向）+树的直径的应用

题目1：L3-032 关于深度优先搜索和逆序对的题应该不会很难吧这件事
题目大意：题当中给了一个树，树上有节点编号（无权值），问在所有的可能dfs排序当中，有多少个逆序对。多个dfs排序的产生是因为在遍历节点的时候是以等概率遍历的。
解题思路：
先来看这个图，这个图里面3是4和5的祖先节点，因此在dfs排序当中，3一定在4和5前面（在所有dfs排序当中），这样的话是不会产生逆序对的。而再看同一层的4和5或者不具有直接父子关系的4和1，对于这样的节点对，他们在dfs排序当中是等概率出现的，也就是一半的dfs排序中，4在1前面，而另一半是1在4前面。

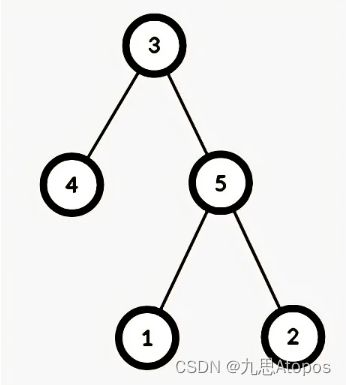
所以说，只要求出祖先节点一定在子节点前面的对数、祖先节点一定不在子节点前面的对数、祖先节点不一定在子节点前面的对数即可。
在求祖先节点在子节点前面的对数的时候只需要用树状数组维护即可。还有就是全部dfs排序的数量为一层子节点的数量阶乘相乘。
代码：

#include
#include
#include
using namespace std;
typedef long long ll;
const int length = 3e5 + 5;
int mod = 1e9 + 7;
vector<vector<int>> edge(length);
int sz[length];
int tree[length];
int kl[length];
int init;
int lowbit(int x)
{
	return x & (-x);
}
void update(int x, int v)
{
	while (x)
	{
		tree[x] += v;
		x = x - lowbit(x);
	}
}
int query(int x)
{
	int ans = 0;
	while (x < length)
	{
		ans =((ll) ans + tree[x])%mod;
		x = x + lowbit(x);
	}
	return ans;
}
int ksm(int base, int t)
{
	int ans = 1;
	while (t)
	{
		if (t % 2 == 1)
		{
			ans = (ll)ans*base%mod;
		}
		base = (ll)base*base%mod;
		t = t >> 1;
	}
	return ans;
}
int dfs(int cur, int fa,int depth)
{
	update(cur, 1);
	int ans = 0;
	for (int j : edge[cur])
	{
		if (j != fa)
		{
			sz[cur]++;
			int a = query(j + 1);
			init = ((ll)init + (depth - a)) % mod;
			ans = ((ll)ans + a) % mod;
			int tmp=dfs(j, cur, depth+1);
			ans = ((ll)ans + tmp) % mod;
		}
	}
	update(cur, -1);
	return ans;
}
int main(void)
{
	int n, r;
	scanf_s("%d%d", &n, &r);
	for (int i = 0; i < n - 1; i++)
	{
		int a, b;
		scanf_s("%d%d", &a, &b);
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	int yh=dfs(r, -1, 1);
	kl[0] = 1;
	for (int i = 1; i <= n; i++)
	{
		kl[i] = (ll)kl[i - 1] * i%mod;
	}
	int sum = 1;
	for (int i = 1; i <= n; i++)
	{
		sum = (ll)sum*kl[sz[i]] % mod;
	}
	int pp = (ll)((ll)n*(n - 1)%mod)*ksm(2, mod - 2)%mod;
	int yh_ = (pp - yh - init + mod) % mod;
	int ans1 = (ll)yh * sum%mod;
	int ans2 = (ll)((ll)yh_*sum)%mod*ksm(2, mod - 2) % mod;
	ans1 = ((ll)ans1 + ans2) % mod;
	printf("%d", ans1);
}

题目2：D. A Wide, Wide Graph
题目大意：给定一棵树，在两个节点间距离至少为k条件下，两点之间有边。在每一个取值k下（1<=k<=n)，求树上有边的节点形成的连通分量数。这个题只要求出树上最远的两个点间的距离，并记录下这两个点，然后求每一个点到这两个点的最大距离，如果这个距离小于k，那么这个点是孤立的。否则可以与两个端点中的一个组成连通分量。也就是求出每一个小于k的距离点数，然后+1(连通分量）使用前缀数组来维护。

#include
#include
#include
#include
using namespace std;
const int length = 1e5 + 5;
vector<vector<int>> edge(length);
int p;
int q;
int dis[length];
int dis1[length];
int cnt[length];
int qianzhui[length];
int ans=-1; 
void dfs(int cur, int fa,int *p,int *dis)
{
	if (dis[cur] > ans)
	{
		ans = dis[cur];
		*p = cur;
	}
	for (int j : edge[cur])
	{
		if (j != fa)
		{
			dis[j] = max(dis[j], dis[cur] + 1);
			dfs(j, cur,p,dis);
		}
	}
}
int main(void)
{
	int n;
	scanf_s("%d", &n);
	for (int i = 0; i < n - 1; i++)
	{
		int a, b;
		scanf_s("%d%d", &a, &b);
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	dfs(1, -1,&p,dis);
	memset(dis, 0, sizeof(dis));
	ans = -1;
	dfs(p, -1,&q,dis);
	dfs(q, -1, &p, dis1);
	for (int i = 1; i <= n; i++)
	{
		int tmp = max(dis[i], dis1[i]);
		cnt[tmp]++;
	}
	for (int i = 1; i <= n; i++)
	{
		qianzhui[i] = qianzhui[i - 1] + cnt[i];
		printf("%d ", min(n,qianzhui[i - 1] + 1));
	}
}