平衡二叉树(AVL树)C++代码实现
目录
-
- 平衡二叉树定义
- A V L AVL AVL树类的封装
- A V L AVL AVL树的插入操作与平衡化
-
- L L LL LL型调整
- R R RR RR型调整
- L R LR LR型调整
- R L RL RL型调整
- A V L AVL AVL树查找操作
- A V L AVL AVL树删除结点操作
- 总源代码
平衡二叉树定义
为了使二叉排序树的平均查找长度更小,需要适当控制树高,显然,控制树高的一个有效措施就是尽量保持树的左右子树高度大致平衡,由此产生了平衡二叉树的概念。
G . M . A d e l s o n − V e l s k i i G.M.Adelson-Velskii G.M.Adelson−Velskii和 E . M . L a n d i s E.M.Landis E.M.Landis在1962年提出了一种平衡二叉树模型,故称为 A V L AVL AVL树。在未声明的情况下,平衡二叉树默认指 A V L 树 AVL树 AVL树。
A V L AVL AVL树是一棵二叉排序树,其或者为空,或者满足以下性质:
1)左右子树高度差的绝对值不大于1
2)左右子树都是平衡二叉树
定义平衡因子来研究AVL树:
结点的平衡因子 B F BF BF=结点的左子树高度-结点右子树高度
A V L AVL AVL树类的封装
struct BBTNode
{
BBTNode*leftson;
BBTNode*rightson;
BBTNode*parent;
int data;
BBTNode(BBTNode*node1,BBTNode*node2,BBTNode*node3)
{
leftson = node1;
rightson = node2;
parent = node3;
}
};
class BBT
{
public:
BBT(int num);
~BBT();
void preorder();
void insert(int element);
bool find(int elemnet);
void del(int element);
void delall();
protected:
void insert(int element, BBTNode*&node, BBTNode*&parent);
int getB_factor(BBTNode*node);
int getheight(BBTNode*node);
void LL(BBTNode*&node);
void LR(BBTNode*&node);
void RR(BBTNode*&node);
void RL(BBTNode*&node);
void preorder(BBTNode*node);
bool find(int element, BBTNode* node);
void del(int element, BBTNode*&node);
void del_directly(BBTNode*&node);
void del_repalce(BBTNode*&node, BBTNode*&son);
void del_reconnect(BBTNode*&node);
void adjust(BBTNode*&node);
void delall(BBTNode*&node);
private:
BBTNode* root;
int num;
};
A V L AVL AVL树的插入操作与平衡化
A V L AVL AVL树的平衡因子为-1,0或1,设计平衡二叉树操作算法的关键在于如何使得平衡二叉树保持平衡。以下四种情况下的插入操作可能会导致原有 A V L AVL AVL树发生不平衡:
- (1) L L LL LL:若某一结点的平衡因子为1,当在其左子树的左子树上插入一个新结点时会导致该结点的平衡因子由1变为2
- (2) R R RR RR:若某一节点的平衡因子为-1,当在其右子树的右子树上插入一个新结点会导致该结点的平衡因子由-1变为-2
- (3) L R LR LR:若某一结点的平衡因子为1,当在其左子树的右子树上插入一个新结点时会导致该结点的平衡因子由1变为2
- (4) R L RL RL:若某一节点的平衡因子为-1,当在其右子树的左子树上插入一个新的结点时会导致该结点的平衡因子由-1变成-2
下面具体介绍如何调整与代码实现
L L LL LL型调整
判断条件:
最低不平衡点的平衡因子为2,新插入结点的值小于最低不平衡点的左儿子结点值

步骤一:将 A A A的左子树 B B B提升为新二叉树的根
步骤二:将原来的 A A A连同右子树 A L A_L AL向下旋转,使其成为 B B B的右子树
步骤三:将B的原右子树 B R B_R BR作为左子树连接到 A A A上
代码实现如下:
在这份代码中,参数node就是图中的 A A A,定义的son就是图中的 B B B,需要注意的是在处理node的父节点与son的关系时,如果node的父节点是NULL的话说明node即是根节点root,则需要将son更新为根节点root的操作,这点后面也有,后面将不再提及。
void BBT::LL(BBTNode*&node)
{
BBTNode* son = node->leftson;
son->parent = node->parent;
if (node->parent == NULL) root = son;
else
{
if (node->data < node->parent->data) node->parent->leftson = son;
else node->parent->rightson = son;
}
if (son->rightson != NULL) son->rightson->parent = node;
node->leftson = son->rightson;
node->parent = son;
son->rightson = node;
}
R R RR RR型调整
判断条件:
最低不平衡点的平衡因子为-2,新插入结点的值大于等于最低不平衡点的右儿子结点值

步骤一:将的右子树提升为新二叉树的根
步骤二:将原来的连同其左子树向下旋转,使其成为的左子树
步骤三:将的原左子树 B L B_L BL作为左子树连接到上
void BBT::RR(BBTNode*&node)
{
BBTNode*son = node->rightson;
son->parent = node->parent;
if (node->parent == NULL) root = son;
else
{
if (node->data < node->parent->data) node->parent->leftson = son;
else node->parent->rightson = son;
}
if(son->leftson!=NULL)son->leftson->parent = node;
node->rightson = son->leftson;
node->parent = son;
son->leftson = node;
}
L R LR LR型调整
判断条件:
最低不平衡点的平衡因子为2,新插入结点的值大于等于最低不平衡点的左儿子结点值

首先执行RR旋转:
步骤一:将的右子树提升为新二叉树的“根”
步骤二:将原来的连同其左子树 B L B_L BL向下旋转,使其成为的左子树
步骤三:将的原左子树 C L C_L CL作为右子树连接到上然后再执行LL旋转:
步骤四:将的左子树提升为新二叉树的根
步骤五:将原来的连同其右子树 A R A_R AR向下旋转,使其成为的右子树
步骤六:将的原右子树 C R C_R CR作为左子树连接到上
void BBT::LR(BBTNode*&node)
{
BBTNode*son = node->leftson;
BBTNode*grandson = son->rightson;
grandson->parent = node->parent;
if (node->parent == NULL) root = grandson;
else
{
if (node->data < node->parent->data) node->parent->leftson = grandson;
else node->parent->rightson = grandson;
}
if(grandson->leftson!=NULL) grandson->leftson->parent = son;
if(grandson->rightson!=NULL) grandson->rightson->parent = node;
son->parent = grandson;
son->rightson = grandson->leftson;
grandson->leftson = son;
node->leftson = grandson->rightson;
node->parent = grandson;
grandson->rightson = node;
}
R L RL RL型调整
判断条件:
最低不平衡点的平衡因子为-2,新插入结点的值小于最低不平衡点的右儿子结点值

首先执行LL旋转
步骤一:将的左子树提升为新二叉树的“根”
步骤二:将原来的连同其右子树 B R B_R BR向下旋转,使其成为的右子树
步骤三:将的原右子树 C R C_R CR作为左子树连接到上
然后再执行RR旋转
步骤四:将的右子树提升为新二叉树的根
步骤五:将原来的连同其左子树 A L A_L AL向下旋转,使其成为的左子树
步骤六:将的原左子树 C L C_L CL作为右子树连接到上
void BBT::RL(BBTNode*&node)
{
BBTNode*son = node->rightson;
BBTNode*grandson = son->leftson;
grandson->parent = node->parent;
if (node->parent == NULL) root = grandson;
else
{
if (node->data < node->parent->data) node->parent->leftson = grandson;
else node->parent->rightson = grandson;
}
if(grandson->leftson!=NULL) grandson->leftson->parent = node;
if(grandson->rightson!=NULL) grandson->rightson->parent = son;
node->parent = grandson;
node->rightson = grandson->leftson;
son->parent = grandson;
son->leftson = grandson->rightson;
grandson->leftson = node;
grandson->rightson = son;
}
了解了4种调整方式便可以编写建树操作或插入操作了。
建树主要是调用插入函数,插入函数的逻辑与一般的二叉排序树相同,都是采用递归插入。只不过多了判断是否平衡,若不平衡则调整。
BBT::BBT(int num)
{
this->num = num;
root = new BBTNode(NULL, NULL, NULL);
for (int i = 1; i <= num; i++)
{
int element;
cin >> element;
if (i == 1)
{
root->data = element;
continue;
}
insert(element, root, root->parent);
}
}
void BBT::insert(int element, BBTNode*&node, BBTNode*&parent)
{
if (node == NULL)
{
BBTNode*s = new BBTNode(NULL, NULL, NULL);
s->data = element;
s->parent = parent;
node = s;
BBTNode* p = node->parent;
int factor = getB_factor(p);
while (factor>=-1&& factor <=1)
{
p = p->parent;
if (p == NULL) break;
factor = getB_factor(p);
}
if (factor == 2)
{
if (element < p->leftson->data) LL(p);
else LR(p);
}
if (factor == -2)
{
if (element < p->rightson->data) RL(p);
else RR(p);
}
}
else if (element >= node->data)
insert(element, node->rightson, node);
else
insert(element, node->leftson, node);
}
void BBT::insert(int element)
{
if (num == 0)
{
root = new BBTNode(NULL, NULL, NULL);
root->data = element;
}
else insert(element, root, root->parent);
num++;
}
A V L AVL AVL树查找操作
查找操作与一般的二叉排序树相同,采用递归查找。
bool BBT::find(int elemnet)
{
return find(elemnet, root);
}
bool BBT::find(int element, BBTNode*node)
{
if (node == NULL) return false;
if (node->data == element) return true;
if (node->data > element) return find(element, node->leftson);
if (node->data < element) return find(element, node->rightson);
}
A V L AVL AVL树删除结点操作
这一节以如图所示平衡二叉树举例
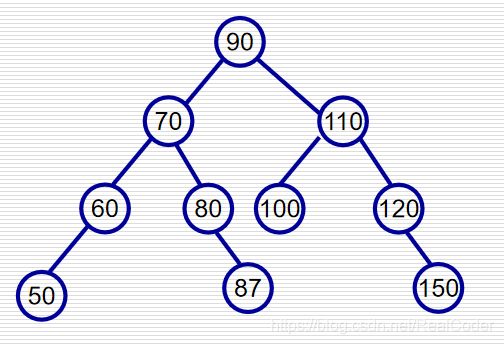
删除结点主要有三种方法,三种方法基于三种情况。但都需要进行调整以维护树的平衡,都调用了adjust函数,这个在后面会阐述具体实现。
情形1:待删除结点是叶子结点,例如删除图中值为50的结点。采用直接删除法,只需delete和断绝其与父节点关系。
void BBT::del_directly(BBTNode*&node)
{
BBTNode* p = new BBTNode(NULL, NULL, NULL);
p = node;
BBTNode* s = p->parent;
if (p->data < s->data) s->leftson = NULL;
else s->rightson = NULL;
delete p;
adjust(s);
}
情形2:待删除结点的度为1,即只有一个子结点,例如图中的值为60的结点。采用顶替法,将待删除结点的子结点放到待删除结点原来的位置上,并与待删除结点的父节点建立关系。
void BBT::del_repalce(BBTNode*&node, BBTNode*&son)
{
BBTNode*p = new BBTNode(NULL, NULL, NULL);
p = node;
BBTNode* s = p->parent;
if (p->data < s->data) s->leftson = son;
else s->rightson = son;
son->parent = s;
delete p;
adjust(s);
}
情形3:待删除结点的度为2,即有2个子结点,采用重新连接法。实现原理为找到比待删除结点值大或相等的最小值的结点。将该结点放置到待删除结点的位置上。寻找的过程就是寻找待删除结点的右子树的最左下方的结点。
例如:删除图中值为90的结点,我们采用重新连接法找到的结点是100。删除图中值为110的结点,我们采用重新连接法找到的结点是120。
细心的朋友可以发现我在这里举了2个例子,是的,因为找到的结点可以分为两种情况。
实际上,情形3是可以转化为前2个情形的,我们大可不必删除我们原来要删除的结点,只需要将找到的结点的值付给原来要删除的结点,这也是一种变相的删除。
但是删除还是不可避免的,我们现在需要删除的是我们找到的结点。
这就可以归类为前两个情形了。
情形3-1:找到的结点是叶子结点,则符合情形1,直接删除。
情形3-2:找到的结点是其父节点的右孩子,则符合情形2,将找到的结点的子树替代我们通过重新连接法找到的结点的位置。
void BBT::del_reconnect(BBTNode*&node)
{
BBTNode*p = new BBTNode(NULL, NULL, NULL);
p = node;
p = p->rightson;
while (p->leftson != NULL) p = p->leftson;
node->data = p->data;
BBTNode* s = p->parent;
if (p->leftson==NULL&&p->rightson==NULL) del_directly(p);
else del_repalce(p, p->rightson);
adjust(s);
}
三份代码中都有adjust函数,现在就来讲讲这个adjust函数。由于删除节点后,不能保证整个树依然处于平衡状态,所以需要由被删除结点位置自下而上进行检查,进行调整。
有人可能有疑问了,这样的话是不是直接把插入时的调整部分的代码拿来copy就可以了?
并不是这样,在那个部分,我们是根据新插入结点的值来判断究竟是什么类型的不平衡情况的。
所以,这里给出一种新的不平衡情况的判断:
- L L LL LL:某一节点的平衡因子为2,其左儿子结点的平衡因子为1
- L R LR LR:某一节点的平衡因子为2,其左儿子结点的平衡因子为-1
- R R RR RR:某一节点的平衡因子为-2,其右儿子结点的平衡因子为-1
- R L RL RL:某一节点的平衡因子为-2,其左儿子结点的平衡因子为1
void BBT::adjust(BBTNode*&s)
{
while (s != NULL)
{
int factor = getB_factor(s);
if (factor == 2)
{
if (getB_factor(s->leftson) == 1) LL(s);
else LR(s);
}
if (factor == -2)
{
if (getB_factor(s->rightson) == 1) RL(s);
else RR(s);
}
s = s->parent;
}
}
删除操作的代码为:
void BBT::del(int element)
{
del(element, root);
}
void BBT::del(int element, BBTNode*& node)
{
if (num == 0||node==NULL) return;
if (num == 1)
{
delete root;
return;
}
if (node->data == element)
{
if (node->leftson == NULL && node->rightson == NULL) del_directly(node);
else if (node->leftson == NULL && node->rightson != NULL) del_repalce(node, node->rightson);
else if (node->leftson != NULL && node->rightson == NULL) del_repalce(node, node->leftson);
else del_reconnect(node);
num--;
return;
}
if (node->data > element) del(element, node->leftson);
if (node->data < element) del(element, node->rightson);
}
总源代码
#include
#include
using namespace std;
struct BBTNode
{
BBTNode*leftson;
BBTNode*rightson;
BBTNode*parent;
int data;
BBTNode(BBTNode*node1,BBTNode*node2,BBTNode*node3)
{
leftson = node1;
rightson = node2;
parent = node3;
}
};
class BBT
{
public:
BBT(int num);
~BBT();
void preorder();
void insert(int element);
bool find(int elemnet);
void del(int element);
void delall();
protected:
void insert(int element, BBTNode*&node, BBTNode*&parent);
int getB_factor(BBTNode*node);
int getheight(BBTNode*node);
void LL(BBTNode*&node);
void LR(BBTNode*&node);
void RR(BBTNode*&node);
void RL(BBTNode*&node);
void preorder(BBTNode*node);
bool find(int element, BBTNode* node);
void del(int element, BBTNode*&node);
void del_directly(BBTNode*&node);
void del_repalce(BBTNode*&node, BBTNode*&son);
void del_reconnect(BBTNode*&node);
void adjust(BBTNode*&node);
void delall(BBTNode*&node);
private:
BBTNode* root;
int num;
};
void BBT::LL(BBTNode*&node)
{
BBTNode* son = node->leftson;
son->parent = node->parent;
if (node->parent == NULL) root = son;
else
{
if (node->data < node->parent->data) node->parent->leftson = son;
else node->parent->rightson = son;
}
if (son->rightson != NULL) son->rightson->parent = node;
node->leftson = son->rightson;
node->parent = son;
son->rightson = node;
}
void BBT::LR(BBTNode*&node)
{
BBTNode*son = node->leftson;
BBTNode*grandson = son->rightson;
grandson->parent = node->parent;
if (node->parent == NULL) root = grandson;
else
{
if (node->data < node->parent->data) node->parent->leftson = grandson;
else node->parent->rightson = grandson;
}
if(grandson->leftson!=NULL) grandson->leftson->parent = son;
if(grandson->rightson!=NULL) grandson->rightson->parent = node;
son->parent = grandson;
son->rightson = grandson->leftson;
grandson->leftson = son;
node->leftson = grandson->rightson;
node->parent = grandson;
grandson->rightson = node;
}
void BBT::RR(BBTNode*&node)
{
BBTNode*son = node->rightson;
son->parent = node->parent;
if (node->parent == NULL) root = son;
else
{
if (node->data < node->parent->data) node->parent->leftson = son;
else node->parent->rightson = son;
}
if(son->leftson!=NULL)son->leftson->parent = node;
node->rightson = son->leftson;
node->parent = son;
son->leftson = node;
}
void BBT::RL(BBTNode*&node)
{
BBTNode*son = node->rightson;
BBTNode*grandson = son->leftson;
grandson->parent = node->parent;
if (node->parent == NULL) root = grandson;
else
{
if (node->data < node->parent->data) node->parent->leftson = grandson;
else node->parent->rightson = grandson;
}
if(grandson->leftson!=NULL) grandson->leftson->parent = node;
if(grandson->rightson!=NULL) grandson->rightson->parent = son;
node->parent = grandson;
node->rightson = grandson->leftson;
son->parent = grandson;
son->leftson = grandson->rightson;
grandson->leftson = node;
grandson->rightson = son;
}
int BBT::getheight(BBTNode*node)
{
if (node == NULL) return 0;
return max(getheight(node->leftson), getheight(node->rightson)) + 1;
}
int BBT::getB_factor(BBTNode*node)
{
return getheight(node->leftson) - getheight(node->rightson);
}
void BBT::insert(int element, BBTNode*&node, BBTNode*&parent)
{
if (node == NULL)
{
BBTNode*s = new BBTNode(NULL, NULL, NULL);
s->data = element;
s->parent = parent;
node = s;
BBTNode* p = node->parent;
int factor = getB_factor(p);
while (factor>=-1&& factor <=1)
{
p = p->parent;
if (p == NULL) break;
factor = getB_factor(p);
}
if (factor == 2)
{
if (element < p->leftson->data) LL(p);
else LR(p);
}
if (factor == -2)
{
if (element < p->rightson->data) RL(p);
else RR(p);
}
}
else if (element >= node->data)
insert(element, node->rightson, node);
else
insert(element, node->leftson, node);
}
BBT::BBT(int num)
{
this->num = num;
root = new BBTNode(NULL, NULL, NULL);
for (int i = 1; i <= num; i++)
{
int element;
cin >> element;
if (i == 1)
{
root->data = element;
continue;
}
insert(element, root, root->parent);
}
}
void BBT::preorder(BBTNode*node)
{
if (node == NULL) return;
cout << node->data << endl;
preorder(node->leftson);
preorder(node->rightson);
}
void BBT::preorder()
{
preorder(root);
}
void BBT::insert(int element)
{
if (num == 0)
{
root = new BBTNode(NULL, NULL, NULL);
root->data = element;
}
else insert(element, root, root->parent);
num++;
}
bool BBT::find(int element, BBTNode*node)
{
if (node == NULL) return false;
if (node->data == element) return true;
if (node->data > element) return find(element, node->leftson);
if (node->data < element) return find(element, node->rightson);
}
bool BBT::find(int elemnet)
{
return find(elemnet, root);
}
void BBT::adjust(BBTNode*&s)
{
while (s != NULL)
{
int factor = getB_factor(s);
if (factor == 2)
{
if (getB_factor(s->leftson) == 1) LL(s);
else LR(s);
}
if (factor == -2)
{
if (getB_factor(s->rightson) == 1) RL(s);
else RR(s);
}
s = s->parent;
}
}
void BBT::del_directly(BBTNode*&node)
{
BBTNode* p = new BBTNode(NULL, NULL, NULL);
p = node;
BBTNode* s = p->parent;
if (p->data < s->data) s->leftson = NULL;
else s->rightson = NULL;
delete p;
adjust(s);
}
void BBT::del_repalce(BBTNode*&node, BBTNode*&son)
{
BBTNode*p = new BBTNode(NULL, NULL, NULL);
p = node;
BBTNode* s = p->parent;
if (p->data < s->data) s->leftson = son;
else s->rightson = son;
son->parent = s;
delete p;
adjust(s);
}
void BBT::del_reconnect(BBTNode*&node)
{
BBTNode*p = new BBTNode(NULL, NULL, NULL);
p = node;
p = p->rightson;
while (p->leftson != NULL) p = p->leftson;
node->data = p->data;
BBTNode* s = p->parent;
if (p->leftson==NULL&&p->rightson==NULL) del_directly(p);
else del_repalce(p, p->rightson);
adjust(s);
}
void BBT::del(int element, BBTNode*& node)
{
if (num == 0||node==NULL) return;
if (num == 1)
{
delete root;
return;
}
if (node->data == element)
{
if (node->leftson == NULL && node->rightson == NULL) del_directly(node);
else if (node->leftson == NULL && node->rightson != NULL) del_repalce(node, node->rightson);
else if (node->leftson != NULL && node->rightson == NULL) del_repalce(node, node->leftson);
else del_reconnect(node);
num--;
return;
}
if (node->data > element) del(element, node->leftson);
if (node->data < element) del(element, node->rightson);
}
void BBT::del(int element)
{
del(element, root);
}
void BBT::delall(BBTNode*&node)
{
if (node == NULL) return;
delall(node->leftson);
delall(node->rightson);
BBTNode* s = new BBTNode(NULL, NULL, NULL);
s = node;
delete s;
}
void BBT::delall()
{
delall(root);
num = 0;
}
BBT::~BBT()
{
delall();
}
int main()
{
//test data:100 90 80 60 70 50 120 110 150 87
BBT Tree(10);
Tree.insert(30);
Tree.preorder();
cout << Tree.find(30) << endl;
cout << Tree.find(999) << endl;
//Tree.del(90);
Tree.del(110);
Tree.preorder();
return 0;
}