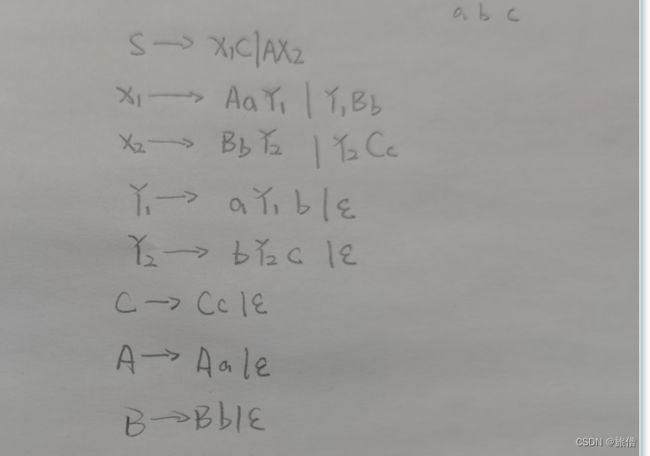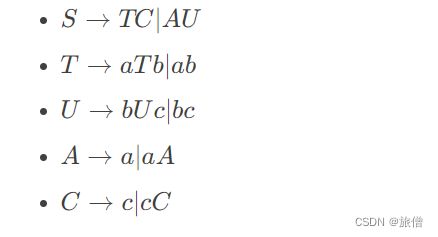形式语言总结
形式语言马上考试了,每天写一点笔记复习一下,更新中ing
第一章DFA
DFA是一种特殊的NFA,
第2章NFA
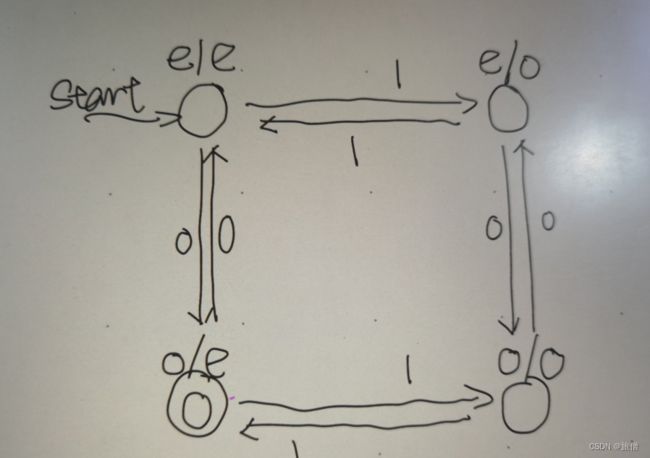
1.设计一个由01构成的串,1是偶数0是奇数的NFA
对0 1的状态进行区分
第3-4章正则表达式
正则表达式的设计举例
正则表达式的运算
正则表达式的优先级
举例
1.倒数第三个字符是1
(0+1)*1(0+1)(0+1)
2.不含有连续的0
(1+01)*(0+![]() )
)
3.含有000
(0+1)*000(0+1)*
4.不含000/111的正则语言(/代表两个式等价的)
(1+01+001)*(![]() +0+00) / 1*(0
+0+00) / 1*(0![]() +00
+00![]() )
)
DFA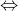 正则表达式
正则表达式
为什么要引入:有的时候我们做设计正则表达式习题的时候发现直接想很困难,我们不如利用正则表达式和DFA之间的等价性,构造出DFA,进而构造正则表达式。
1.设计不含001/110的正则表达式
2.设计不含010/101的正则表达式
方法1:直接猜测法:
![]()
方法2:DFA转正则表达式
3.设计不含001/110的正则语言
4 . L = { w∈{0,1}* | w contains both 01 and 10 as substrings }
这个题的出错点在于可能忘记考虑010 101的情况
分类相加的方法:
直接的方法 :合并情况的方法
![]()
5.The set of all strings with an equal number of 0's and 1's, such that no prefix has two more 0's than 1's, nor two more 1's than 0's.
![]()
6. Let L={ w | w∈{0,1}* and if there are two 0s of w, they must be separated by 1 or 11 }
![]()
|11 | 11 |
explaination : ![]() | 10 | 10 |................................
| 10 | 10 |................................
正则语言的性质
1.证明泵引理
- 往多泵
- 往少泵
- 利用语言的封闭性证明:if
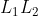 都是正则语言L =
都是正则语言L = 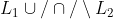 ,或者其反转
,或者其反转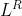 也是正则语言,如果不是正则语言那么L不一定不是正则语言。
也是正则语言,如果不是正则语言那么L不一定不是正则语言。
具体实例见第四章习题,一般的方法是取语言中的子串。利用语言中的一个元素不是正则来确定不是正则语言。
2.DFA的最小化:
第5章上下文无关文法:
设计文法:
举例
设计文法的关键在于理解递归性,文法是一个迭代器
1.The set {![]() | i ≠ j or j ≠ k}, that is, the set of strings of a's followed by b's followed by c's, such that there are either a different number of a's and b's or a different number of b's and c's, or both.
| i ≠ j or j ≠ k}, that is, the set of strings of a's followed by b's followed by c's, such that there are either a different number of a's and b's or a different number of b's and c's, or both.
上方的做法是错误的做法 因为没有考虑i=j=k的情况。
修改之后的结果
2.The set {![]() |i=j|j=k} is generated by G = ( { S , T , U , A , C } , { a , b , c } , P , S )) with production P:
|i=j|j=k} is generated by G = ( { S , T , U , A , C } , { a , b , c } , P , S )) with production P:
3.请为语言L = {![]() }设计文法
}设计文法
4.设计0、1构成的串的文法,0 1数量不相等.
5. The set of all strings 0’s and 1’s that are not of the form ww, that is , not equal to any string repeated.
6.The set of all strings with twice as many 0's as 1's.
![]()
7.设计 Lj≥2i = {aibj | j ≥ 2i} 的文法.
- S→AB
- A→aAbb I 空串
- B→Bb I 空串
8. L= { ![]() | n
| n ![]() 0 and n
0 and n![]() 3}
3}
9.L(0 0* 11* 22* 00* 11* 22* 00* 11* 22*) Hint : The language defined by the regular expression.
分析:看起来像是012202012然后每一个的子字符可以重复,![]()
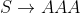 相当于三次方
相当于三次方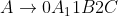
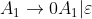
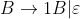
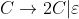
10. L = { ![]() |}
|}
explaination:分成两种情况:![]()
![]()
![]()
11.L ={ ![]() }
}
验证某个串是否在文法中:派生 使用树来判断字符串是否在文法中
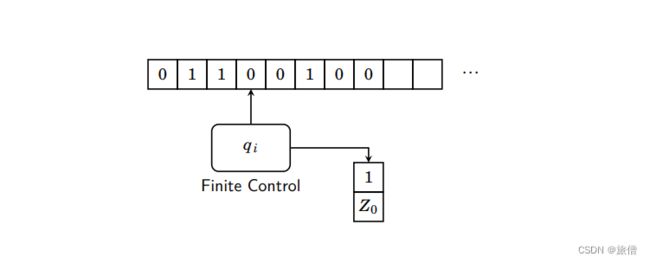
第6章下推自动机
下推自动机相当于 ![]() 栈:他既有非确定性也支持空转移,他拥有栈的性质,体现在它能够识别w
栈:他既有非确定性也支持空转移,他拥有栈的性质,体现在它能够识别w![]() 但是不能识别ww和
但是不能识别ww和![]() (图灵机可以识别)语言。
(图灵机可以识别)语言。
将000入栈,每读入一个1弹出一个0....当输入完所有的1栈空,则就是识别0n1n的PDA
每次根据读头、状态、栈顶三个东西进行跳转,修改当前状态、改变读头,弹出一个符号往栈里压入多个符号 多个符号构成的字符串的长度可以是0个1个或者多个,0个代表弹出栈顶元素,1个代表保持或者修改栈顶符号,多个表示弹出一个符号压入多个符号。
PDA的设计
1.设计识别{![]() |n
|n![]() 1}的PDA
1}的PDA
2.升级版设计识别{![]() |n
|n![]() 0}的PDA
0}的PDA
*思考:1当识别0001111扫描完整个串的空串才能停下来在q3接受状态如果后边还有字符他会卡死Z0可以判断是否扫描完整个串.2.000111我00之间也可以通过空转移到达q2但是此时读头上是0,而我只能接受1的读字符串的动作因此会卡死,由于PDA具有非确定性,只有在wwr的形式上才能接受,否则就会卡死。
3.设计识别{w![]() |w
|w![]()
![]() }的PDA
}的PDA
PDA性质
由于PDA具有非确定性,仅用状态无法很好描述当前的性质
![]()
终态方式和空栈方式接受PDA