【支持向量机SVM系列教程3】支持向量回归SVR

3 支持向量回归SVR

使用支持向量机算法不仅能解决分类问题，还能解决回归问题。

3.1 解决的目标

支持向量回归所要解决的问题是：对于给定如下的的训练数据集，

$$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2)...,({\mathbf{x}}_m,y_m)\},y_i\in \mathbb{R}$$
找到一个决策边界（或决策超平面）：
$$f(x)={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$
使得模型对样本${\mathbf{x}}_i$的预测值 $f({\mathbf{x}}_i)$与标签$y_i$之间的距离尽可能小。下面就将介绍如何实现这个目标。

3.2 偏差 $ϵ$ 的理解

偏差 $ϵ$ 是支持向量回归中一个非常重要的概念，它表示SVR对样本${\mathbf{x}}_i$的预测值$f(x_i)$与标签$y_i$之间的偏差的容忍度，也就是说，SVR能容忍$f(x_i)$与$y_i$中间最多有$ϵ$ 的偏差。当两者时间的偏差小于$ϵ$ 时，损失为0；当两者之间的偏差不小于$ϵ$ 时，损失不为0。这个损失可以由如下的公式表达出来：
$$l_{ϵ}(f({\mathbf{x}}_i)-{\mathbf{y}}_i)=\{\begin{array}{r}0,|f({\mathbf{x}}_i)-y_i|⩽ϵ\\ |f({\mathbf{x}}_i)-y_i|-ϵ,|f({\mathbf{x}}_i)-y_i|>ϵ\end{array}$$
该损失函数称为 $ϵ$-不敏感损失函数，它用来衡量SVR问题中各个样本的损失。

为了能够使读者更好地理解$ϵ$ ，下面绘制出了$ϵ$ 在二维空间中的表达形式：

上图各部分的含义为：

• 中间深红色的线是SVR找出的决策边界；
• 由两条虚线夹着的浅红色区域称为“隔离带”，其宽度为$2ϵ$,位于隔离带内的样本是预测值$f(x_i)$与标签$y_i$之间的偏差小于$ϵ$ 的样本，由于它们在SVR所能容忍的范围之内，所以SVR将它们的损失视为0；
• 位于浅红色部分之外的样本是预测值$f(x_i)$与标签$y_i$之间的偏差大于$ϵ$ 的样本，它们是SVR中的支持向量，误差为 $|f({\mathbf{x}}_i)-y_i|-ϵ$ 。

3.3 目标函数的转化

经过上面的分析，可以发现：隔离带越大，损失为0的样本的数量越多。SVR问题的目标函数可转化为如下的形式：
KaTeX parse error: Unknown column alignment: 1 at position 150: …{\begin{array}{1̲} \min_{\boldsy…
其中 $C$ 为惩罚系数，起到了约束 $ϵ$ 的作用。具体作用如下：

• 当 $C\to +\infty$时，$ϵ$ 必须为0，此时SVR退化为传统回归模型（传统的回归模型对模型没有容忍度，只有当预测值$f({\mathbf{x}}_i)$与标签$y_i$完全相同时，损失才为0）；
• 当$C$为有限值时，$C$越大，$ϵ$ 的值应越小，隔离带越窄，隔离带内的样本（回归损失为0）越少，SVR模型过拟合的风险越大；而当 $C$ 的值太小时，$C$ 对 $ϵ$ 的惩罚作用过大，$ϵ$发挥作用的空间很小。所以，为了取得良好的泛化性能，同时减小过拟合的风险，$C$的取值必须适中。在实际使用中，$C$是调参的重点对象。

上述目标函数的表达过于冗长，所以为了使得目标函数的表达更加简洁，我们在其基础上引入了松弛变量。令：
$${\xi }_i+{\xi }_i=l_{ϵ}(f({\mathbf{x}}_i)-{\mathbf{y}}_i)$$
此时SVR的目标函数可改写为：
$$\begin{gathered} \underset{\mathbf{w},b,{\xi }_i,{\xi }_i}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m({\xi }_i+{\xi }_i) \\ s.t.f({\mathbf{x}}_i)-y_i⩽ϵ+{\xi }_i \\ {y}_i-f({\mathbf{x}}_i)⩽ϵ+{\xi }_i \\ {\xi }_i⩾0, \\ {\xi }_i⩾0 \end{gathered}$$

3.4 SVR问题的对偶化

在SVC部分我们对目标函数进行了对偶化，简化了原问题的求解过程，并通过对偶化将二维样本的分类扩展到了更高维样本的分类，实现了从线性分类到非线性分类的扩展。对于SVR问题也可以采用这样的思路，将线性回归扩展到非线性回归。参照SVC问题的拉格朗日公式，可得到SVR问题的拉格朗日公式如下:
$$\begin{gathered} L(\mathbf{w},b,\mathbf{\alpha },\mathbf{\alpha },,{\mathbf{\xi }}_i,{\mathbf{\xi }}_i,\mathbf{\lambda },{\mathbf{\lambda }}_i)= \\ \frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m({\xi }_i+{\xi }_i)-\sum _{i=1}^m{\lambda }_i{\xi }_i-\sum _{i=1}^m{\lambda }_i{\xi }_i+ \\ \sum _{i=1}^m{\alpha }_i(f({\mathbf{x}}_i)-y_i-ϵ-{\xi }_i))+\sum _{i=1}^m{\alpha }_i(y_i-f({\mathbf{x}}_i)-ϵ-{\xi }_i) \end{gathered}$$
由KKT中的Stationary条件（当原变量和对偶变量的梯度为0时，优化效果达到最好，无法继续优化），我们可得到如下公式：

• 对 $\mathbf{w}$ 的梯度为0：

KaTeX parse error: Got function '\boldsymbol' with no arguments as subscript at position 19: …igtriangledown_\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲ ̲w L=\boldsymbol…

• 对 $b$ 的梯度为0：
  KaTeX parse error: Got function '\boldsymbol' with no arguments as subscript at position 19: …igtriangledown_\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲ ̲b L =\sum_{i=1}…

• 对 ${\xi }_i$ 的梯度为0：
  $$\begin{gathered} {▽}_{{\xi }_i}L=C-{\alpha }_i-{\lambda }_i=0 \\ \Downarrow \\ C={\alpha }_i+{\lambda }_i \end{gathered}$$

• 对 ${\xi }_i$ 的梯度为0：
  $$\begin{gathered} {▽}_{{\xi }_i}L=C-{\alpha }_i-{\lambda }_i=0 \\ \Downarrow \\ C={\alpha }_i+{\lambda }_i \end{gathered}$$

将上面得到的四个条件代入SVR问题的拉格朗日函数中，得到SVR的对偶问题如下：
$$\begin{gathered} \underset{\mathbf{\alpha },\mathbf{\alpha }}{\max }\sum _{i=1}^m{y}_i({\alpha }_i-{\alpha }_i)-ϵ({\alpha }_i+{\alpha }_i)-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\alpha }_i-{\alpha }_i)({\alpha }_j-{\alpha }_j){\mathbf{x}}_i^T{\mathbf{x}}_j \\ s.t.\sum _{i=1}^m({\alpha }_i-{\alpha }_i)=0,0⩽{\alpha }_i{\alpha }_i⩽C \end{gathered}$$
上面我们已经求得了 $w$ 的表达式。将该式代入$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$ 中，得：
$$f(\mathbf{x})=\sum _{i=1}^m({\alpha }_i-{\alpha }_i){\mathbf{x}}_i^T\mathbf{x}+b$$
再由KKT条件中的Complementary Slackness（松弛补偿）条件（不等式取等号时，约束条件最严格），得：
$$f(\mathbf{x})-ϵ=\sum _{i=1}^m({\alpha }_i-{\alpha }_i){\mathbf{x}}_i^T\mathbf{x}+b-ϵ=y_i$$
求得：
$$b=y_i+ϵ-\sum _{i=1}^m({\alpha }_i-{\alpha }_i){\mathbf{x}}_i^T\mathbf{x}$$
故：
$$f(\mathbf{x})=\sum _{i=1}^m({\alpha }_i-{\alpha }_i){\mathbf{x}}_i^T\mathbf{x}+y_i+ϵ-\sum _{i=1}^m({\alpha }_i-{\alpha }_i){\mathbf{x}}_i^T\mathbf{x}$$
这样就通过对偶化求解出了SVR的原问题。

将上式中的 ${\mathbf{x}}_i^T\mathbf{x}$ 替换成核函数$\kappa (\mathbf{x},{\mathbf{x}}_i)$，就可以将线SVR问题扩展到高维空间中。sklearn中对 $\kappa (\mathbf{x},{\mathbf{x}}_i)$ 主要有高斯核和多项式核两种实现方法。

3.5 sklearn中的支持向量回归

sklearn中对支持向量回归进行了实现，对应的API分别为LinearSVR（用于线性回归）和SVR（用于非线性回归）。

3.5.1 LinearSVR

原型
class sklearn.svm.LinearSVR(*, epsilon=0.0, tol=0.0001, C=1.0, loss='epsilon_insensitive', fit_intercept=True, intercept_scaling=1.0, dual=True, verbose=0, random_state=None, max_iter=1000)
常用参数

• epsilon：浮点数类型，默认值为0.0，表示$ϵ$-不敏感损失函数中的参数$ϵ$；
• tol：浮点数类型，默认值为$10^{-4}$，表示对损失的容忍度，损失降低到 tol 时，停止训练；
• C：浮点数类型，默认值为1.0，表示惩罚系数，起到平衡松弛变量的作用。C 必须为正数
• loss：指定损失函数，默认为’epsilon_insensitive’，表示损失函数的类型；
• random_state：整型，默认为None，用于设置相同的随机数种子，确保多次运行所生成的随机数状态均一致，便于调参与观察；
• max_iter：整型，默认值为1000，表示最大迭代次数。

属性

• coef_：表示学习到的权重 $\mathbf{w}$（在上面的公式推导中已介绍）;
• intercept_：表示学习到的偏置 $\mathbf{b}$（在上面的公式推导中已介绍）;
• n_iter_：对所有类型的所有样本的总迭代次数。

常用方法

• fit(X, y[, sample_weight])：对给定的数据集进行拟合；
• predict(X)：对新数据集 $X$ 进行预测。

3.5.2 SVR

原型
class sklearn.svm.SVR(*, kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)
常用参数

• kernel：用于指定核函数的类型，默认为’ rbf '（高斯核），其他常用的核函数还有：
  • ’ poly '：多项式核
  • ‘ linear ’：线性核（此时等价SVR的功能等价于LinearSVR）
  • ‘ sigmoid ’：sigmoid核
• degree：整型，默认值为3，用于指定多项式核的次数（当且仅当kernel='poly'时有效，指定为其他核函数时自动忽略该参数）
• gamma：字符串类型，默认为’scale’
  • scale：gamma的值为 $1/(n\_features\times X.var())$
  • auto： gamma的值为 $1/n\_features$
• epsilon：浮点数类型，默认值为$0.1$（LinearSVR中该参数默认为 $0.0$），表示 $ϵ$-不敏感损失函数中的参数 $ϵ$；
• tol：浮点数类型，默认值为$10^{-3}$（LinearSVR中该参数默认为$10^{-4}$），损失降低到 tol 时，停止训练；
• C：浮点数类型，默认值为1.0，表示惩罚系数，起到平衡松弛变量的作用。C 必须为正数
• loss：指定损失函数，默认为’epsilon_insensitive’，表示损失函数的类型；
• max_iter：整型，默认值为 $-1$（LinearSVR中该参数默认为$1000$），表示最大迭代次数，默认值$-1$表示对最大迭代次数不做限制。

属性

• coef_：表示学习到的权重 $\mathbf{w}$（在上面的公式推导中已介绍）;
• intercept_：表示学习到的偏置 $\mathbf{b}$（在上面的公式推导中已介绍）;
• support_：表示所有支持向量（位于隔离带以外的样本）的索引；
• support_vectors_：表示所有支持向量。

常用方法

• fit(X, y[, sample_weight])：对给定的数据集进行拟合；
• predict(X)：对新数据集 $X$ 进行预测。

下面的实例将对上述API进行使用，加深读者对上述API的理解。

3.6 实例3：sklearn中支持向量回归(SVR)的对比与分析

支持向量回归和支持向量机分类的基本思想虽然有所不同，但本质是类似的。

SVM分类（包括线性分类和非线性分类）实际上就是找到一个决策边界或决策超平面，使得分类的间隔最大化；而SVR回归（包括线性回归和非线性回归）实际上就是找到一个回归平面，让数据集中的所有样本点到该平面的距离最近。

在sklearn中对支持向量回归进行了实现，对应的类为LinearSVR和 SVR，它们的参数、方法、属性等与LinearSVM和 SVM很类似，这里不再写出它们的API细节，读者可以去查阅官方文档，这里注重于对API的使用。

本实例将对比LinearSVR和 SVR在时间性能和回归拟合效果上的差异，总结出各自的优劣。

3.6.1 创建数据集

首先需要创建数据集。这里为了便于读者理解，选用的是一个自定义的简单数据集，这样有利于简化读者的理解难度。创建数据集的代码如下：

# 创建随机数种子
rng = np.random.RandomState(0)
# 生成10000个范围为0到5的随机数，作为训练集
X = 5 * rng.rand(10000, 1)
# 定义回归的目标为训练集中每个样本的正弦值
y = np.sin(X).ravel()

# 每5步为回归目标添加一次随机噪声
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))

生成的数据集如下图所示：

plt.figure(figsize=(10, 6))
plt.scatter(X[:200], y[:200], c='g', label='data', zorder=1, edgecolors=(0, 0, 0))
plt.xlabel("X_200")
plt.ylabel("y_200", rotation=0)
plt.show()

该数据集呈现出正弦曲线的走势，但是在每5个样本中就加入了一个随机噪声。通过以上方法所定义的数据集是完全随机、没有顺序的。下面定义出测试集。测试集是从0到10之间的十万个等距样本点。之所以取这么多个点，是因为用到了”微积分“的思想——想要在一定范围内画出连续回归预测曲线，就要在该范围内堆砌大量的点，这样才能画出连续的预测曲线。并且，不管是线性SVR还是非线性SVR，对于1维的数据，回归拟合和回归预测的速度都是非常快的，为了能够对比出时间差异，就必须堆砌大量的一维样本点。测试集的定义如下：

X_test = np.linspace(0, 5, 100000)[:, None]

注意：必须加[:, None]索引，因为np.linspace(0, 10, 100000)返回的是一整个数组，加上了

[:, None] 索引才能将整个数组拆分成一个一个的单独数组（代表一个个样本点）。

下面打印出 X_test ：

array([[0.00000e+00],
[5.00005e-05],
[1.00001e-04],
…,
[4.99990e+00],
[4.99995e+00],
[5.00000e+00]])

3.6.2 通过网格搜索找到最佳回归模型

首先先定义出三个不同的模型。这三个模型分为两大类：一类是线性SVR模型，一类是非线性SVR模型。其中非线性SVR模型又分为多种不同的核，常用的有高斯核和多项式核。对这三种模型进行定义的代码如下：

# 定义非线性SVR模型(使用高斯核)
rbf_svr_model = SVR(kernel='rbf', gamma=0.1)

# 定义非线性SVR模型(使用高斯核)

poly_svr_model = SVR(kernel='poly', gamma=0.1)

# 定义线性SVR模型
linear_svr_model = LinearSVR()

接下来对上面三种模型分别进行网格搜索，寻找出各自的最佳参数组合。

# 定义对高斯核SVR模型的网格搜索
rbf_svr_grid = GridSearchCV(rbf_svr_model,
                   param_grid={"C": [1, 10, 100, 1000],
                               # gamma的搜索范围定为 [0.01, 0.1, 1, 10, 100]，下面的写法更加简略
                               "gamma": np.logspace(-2, 2, 5)},
                           n_jobs=-1)
rbf_svr_grid.fit(X[:200], y[:200])

# 定义对多项式核SVR模型的网格搜索
poly_svr_grid = GridSearchCV(poly_svr_model,
                   param_grid={"C": [1, 10, 100, 1000],
                               "degree":  [2 ,3, 4, 5, 6]},
                            n_jobs=-1)
poly_svr_grid.fit(X[:200], y[:200])

# 定义对线性SVR模型的网格搜索
linear_svr_grid = GridSearchCV(linear_svr_model,
                   param_grid={"C": [1, 10, 100, 1000]},
                              n_jobs=-1)
linear_svr_grid.fit(X[:200], y[:200])

接下来获取三种模型的最佳参数组合，代码如下：

# 获取最佳SVR参数组合
print(rbf_svr_grid.best_params_)
# 获取最佳LinearSVR参数
print(poly_svr_grid.best_params_)
# 获取最佳LinearSVR参数
print(linear_svr_grid.best_params_)

输出结果如下：

{‘C’: 1000, ‘gamma’: 0.01}
{‘C’: 1, ‘degree’: 2}
{‘C’: 1}

3.6.3 模型拟合和预测时间的计算

先获取三个模型拟合数据集的时间。代码如下：

# 高斯核svr模型拟合数据的时间
t0 = time.time()
rbf_svr_best = SVR(kernel='rbf', C=1000.0, gamma=0.01)
rbf_svr_best.fit(X[:200], y[:200])
"""
这里有一个小技巧：
上面两行代码可以替换为：svr_grid.best_estimator_.fit(X[:200], y[:200])，
通过best_estimator_属性即可很方便地访问网格搜索总所得到的最佳参数组合所对应的模型

"""
t1= time.time()
rbf_svr_fit_time =t1 - t0
print("Gaussian SVR complexity and bandwidth selected and model fitted in %.6f s" % rbf_svr_fit_time)

# 多项式核svr模型拟合数据的时间
t2 = time.time()
poly_svr_grid.best_estimator_.fit(X[:200], y[:200])
t3= time.time()
poly_svr_fit_time = t3 - t2
print("Polynomial SVR complexity and bandwidth selected and model fitted in %.6f s" % poly_svr_fit_time)

# 线性核SVR模型拟合数据的时间
t4 = time.time()
linear_svr_grid.best_estimator_.fit(X[:200], y[:200])
t5 = time.time()
linear_svr_fit_time = t5 - t4
print("Linear SVR complexity and bandwidth selected and model fitted in %.6f s" % linear_svr_fit_time)

输出结果：

Gaussian SVR complexity and bandwidth selected and model fitted in 0.016470 s

Polynomial SVR complexity and bandwidth selected and model fitted in 0.004990 s

Linear SVR complexity and bandwidth selected and model fitted in 0.003990 s

再获取三个模型预测测试集的时间。代码如下：

# 最佳高斯核svr模型在测试集上的预测的时间
rbf_svr_best = rbf_svr_grid.best_estimator_
rbf_svr_best.fit(X[:200], y[:200])
t0 = time.time()
rbf_svr_y = rbf_svr_best.predict(X_test)
t1 = time.time()
rbf_svr_predict_time = t1 - t0
print("Gaussian SVR prediction for %d inputs in %.6f s" % (X_test.shape[0], rbf_svr_predict_time))

# 最佳多项式核svr模型在测试集上的预测的时间
poly_svr_best = poly_svr_grid.best_estimator_
poly_svr_best.fit(X[:200], y[:200])
t2 = time.time()
poly_svr_y = poly_svr_best.predict(X_test)
t3 = time.time()
poly_svr_predict_time = t3 - t2
print("Polynomial SVR prediction for %d inputs in %.6f s" % (X_test.shape[0], poly_svr_predict_time))

# 最佳线性核svr模型在测试集上的预测的时间
linear_svr_best = linear_svr_grid.best_estimator_
linear_svr_best.fit(X[:200], y[:200])
t4 = time.time()
linear_svr_y = linear_svr_best.predict(X_test)
t5 = time.time()
linear_svr_predict_time = t5 - t4
print("Linear SVR prediction for %d inputs in %.6f s" % (X_test.shape[0], linear_svr_predict_time))

输出结果如下：

Gaussian SVR prediction for 100000 inputs in 0.172031 s

Polynomial SVR prediction for 100000 inputs in 0.217375 s

Linear SVR prediction for 100000 inputs in 0.001993 s

3.6.4 绘图比较

将上述结果绘制成曲线，直观比较出三者在时间性能和拟合效果上的差异上的差别。

plt.figure(figsize=(10,6))

# 获取并画出高斯核SVR中的支持向量（用红色表示）
rbf_svr_sv_index = rbf_svr_best.support_
plt.scatter(X[rbf_svr_sv_index], y[rbf_svr_sv_index], c='r', s=50, label='Gausssian SVR support vectors', zorder=2, edgecolors=(0, 0, 0))


# 画出训练集中的前200个样本点
plt.scatter(X[:200], y[:200], c='k', label='data', zorder=1, edgecolors=(0, 0, 0))

# 画出高斯核SVR的回归拟合效果，并标注出拟合、预测的时间
plt.plot(X_test, rbf_svr_y, c='r', label='Gaussian SVR (fit time: %.6fs, predict time: %.6fs)' % (rbf_svr_fit_time, rbf_svr_predict_time))
# 画出多项式核SVR的回归拟合效果，并标注出拟合、预测的时间
plt.plot(X_test, poly_svr_y, c='g', label='Polynomial SVR (fit time: %.6fs, predict time: %.6fs)' % (poly_svr_fit_time, poly_svr_predict_time))
# 画出线性核SVR的回归拟合效果，并标注出拟合、预测的时间
plt.plot(X_test, linear_svr_y, c='b', label='Linear SVR (fit time: %.6fs, predict time: %.6fs)' % (linear_svr_fit_time, linear_svr_predict_time))

plt.xlabel('data')
plt.ylabel('target')
plt.title('SVR versus Kernel Ridge')
plt.legend()

输出结果如下：

为了方便表达，便于读者理解，下面用G表示高斯核SVR，用P表示多项式核SVR，用L表示线性核SVR。 通过观察上图，可以发现，在拟合数据集的时间上，G(0.016470s) > P(0.004900s) > L(0.003990s)，G的拟合时间远远大于其他两者，而P和L的拟合时间则相近，P大约为L的1到2倍（这实际上是2次核和1次核的时间复杂度的比例）。 在预测测试集（测试集有的十万个样本，所以耗费的时间反而比拟合时间多，而并不是预测时间多于拟合时间）上，P(0.217375s) > G(0.172031s) > L(0.001993s)，P和G预测测试集的时间非常相近，而L则远远快于P和G。综上两点，L在本次任务中的时间性能是最优的。 但是时间性能最优并不能代表拟合的效果最优。观察三者的拟合曲线，可以看到，L（蓝色）曲线的走势与数据集并不吻合，而拟合时间最多的G的拟合曲线与数据集的走势最为吻合，因为它用更多的时间换取了更好的决策超平面。P的拟合效果则次之，比G差，但比L好。 由此可以得出：线性SVR不论是拟合数据集的时间还是预测测试样本的时间均快于非线性SVR，但是，对于这个非线性的数据集，线性SVR的拟合效果比非线性SVR差很多。

3.6.5 误差分析

上面只是从感性认识上辨别三者拟合效果的好坏，为了从更严谨，还是需要”用数值说话“。下面将绘制出三者的均方误差随训练集样本数量变化的学习曲线，从误差分析的角度比较三者的拟合效果。代码如下：

plt.figure(figsize=(10,6))

# 高斯核SVR的学习曲线
train_sizes_rbf, train_scores_rbf, test_scores_rbf = \
    learning_curve(rbf_svr_best, X[:200], y[:200], train_sizes=np.linspace(0.1, 1, 20),
                   scoring="neg_mean_squared_error", cv=10)
plt.plot(train_sizes_rbf, -test_scores_rbf.mean(1), 'o-', color="r", label="Gaussian SVR")

# 多项式核SVR的学习曲线
train_sizes_poly, train_scores_poly, test_scores_poly = \
    learning_curve(poly_svr_best, X[:200], y[:200], train_sizes=np.linspace(0.1, 1, 20),
                   scoring="neg_mean_squared_error", cv=10)
plt.plot(train_sizes_poly, -test_scores_poly.mean(1), 'o-', color="g", label="Polynomial SVR")

# 线性核SVR的学习曲线
train_sizes_linear, train_scores_linear, test_scores_linear= \
    learning_curve(linear_svr_best, X[:200], y[:200], train_sizes=np.linspace(0.1, 1, 20),
                   scoring="neg_mean_squared_error", cv=10)
plt.plot(train_sizes_linear, -test_scores_linear.mean(1), 'o-', color="b", label="Linear SVR")

plt.xlabel("Train size")
plt.ylabel("MSE")
plt.title('Learning curves')
plt.legend(loc="best")

plt.show()

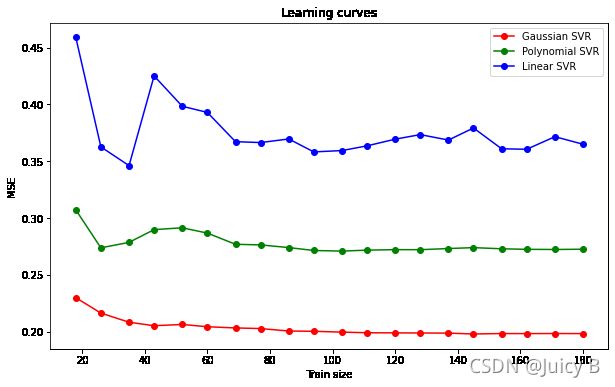
输出结果：

通过观察学习曲线可以看到，不论训练集的样本数取多少，在均方误差MSE上，G均最低，P次之，L最差。这从数值上阐述了P的拟合效果最好的原因。
通过这个例子，可以总结出在使用支持向量回归完成非线性回归任务时需要注意的地方：

1. 线性SVR虽然很快，但是在非线性数据集中拟合的误差很大，所以应该避免在非线性回归问题上使用线性SVR；
2. 对于高斯核SVR，它的拟合时间较长，但是所带来的均方误差较低，拟合效果好，而多项式核SVR的拟合时间相比高斯SVR更快，但是误差更高。读者应该视实际问题，在时间和精度上做出折衷选择。