REC系列:Rethinking and Improving Feature Pyramids for One-Stage Referring Expression Comprehension论文笔记
REC系列:Rethinking and Improving Feature Pyramids for One-Stage Referring Expression Comprehension论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
-
- A、参考表达式理解
- B、特征金字塔
- 四、初步的模型
-
- A、编码器模块
-
- 1、语言编码器
- 2、图像编码器
- B、融合模块
-
- 1、融合策略1️⃣
- 2、融合策略2️⃣
- 2、融合策略3️⃣
- C、Neck
- D、检测头
- E、初步分析及结论
-
- 1、单尺度 vs. 多尺度
- 2、平均 vs. FPN
- 3、FPN 可视化分析
- 五、提出的方法
-
- A、整体结构
- B、语言门
- C、统一门
- 六、实验
-
- A、实验设置
-
- 1、数据集
- 2、实施细节
- B、与不同 Backbones 的 SOTA 模型比较。
- C、消融实验
-
- 1、融合策略
- 2、检测头
- 3、不同的细节
- 4、激活函数
- 5、不同的深度
- 七、定性结果
-
- A、定性样本
- B、可视化
- 八、结论
写在前面
2023 flag:每周一篇博文,本周加更一篇博文,目前还差4篇未补,冲冲冲~
- 这篇论文与三大顶会对比,新颖性不算特别高,重在启发模型的设计细节与研究思路
- 论文地址:Rethinking and Improving Feature Pyramids for One-Stage Referring Expression Comprehension
- 代码地址:论文原文未提供
- 收录于:IEEE TIP 2022
一、Abstract
首先点出参考表达式理解 Referring Expression Comprehension (REC) 的重要性,目前单阶段的方法通常将这一任务视为基于语言条件的目标检测任务,并设计多种融合策略、阶段以及检测头。然而这些方法大多忽略了多尺度特征的整合甚至仅采用单尺度的特征来定位目标。本文重新思考并优化了单阶段框架中的特征金字塔模型。实验表明:尽管多尺度融合有效,目标检测中的 neck(FPN、BFN、HRFPN)对性能有一定的限制,可视化 FPN 的输出之后发现主要是粗糙-细粒度的 FPN 融合策略存在语言混乱问题。于是本文提出一组语言引导的 FPN 方法:Language-Guided FPN (LG-FPN),通过堆叠语言门 language-gate 和 联合门 union-gate 能够动态地分类并选择细粒度的信息。实验表明 LG-FPN 有效且能够应用于不同的视觉 backbone 网络、融合策略及检测头。
二、引言
REC 的定义、意义、难点。早期的两阶段方法将其视为区域检索问题,缺点:对于第一阶段中生成的 proposal 质量敏感;proposal-and-rank 框架计算成本大。最近的单阶段方法直接定位目标,创新之处一般在于设计融合策略、阶段以及检测头。如下图所示:

本文关注单阶段的方法,其被视为一种基于语言的目标检测任务,相应的模型划分为三个部分:backbone,neck,detection head。其中 Neck 一般都是各种各样的 FPN,然而大量的工作通常采用平均策略来融合多尺度特征或仅采用单尺度的特征来定位目标。有文献表明 FPN 或者多头机制会损害性能。于是问题来了:对于 REC 而言,多尺度的特征整合是否有益?目标检测领域的离线 neck 能否更合适?
本文首先尝试回答第一个问题,实验发现多尺度融合比单尺度特征好,但效果有限。于是引用 Grad-CAM 来可视化 FPN 的输出,结果表明简单地使用粗糙-细粒度的 FPN 方法会导致语义混乱。
为充分利用特征金字塔以及减轻语义混乱问题,本文重新思考了 REC 多尺度特征中的语言,因为其包含低层和高层语义,这能选择有效的信息并避免混淆相似的目标。于是提出语言引导的 FPN:LG-FPN,能够动态地基于多模态输入选择网格层次的特征。具体来说,首先使用语言注意力操作和非线性门控函数来计算 VL 特征的关联性并给每一个网格赋值。之后,通过一个数据独立的联合门,提炼整合到的多尺度特征。在深度通道上堆叠这些门控单元,可以自适应地聚合多尺度语义特征。实验表明 LG-FPN 有效且可靠。贡献如下:
- 对多尺度特征进行系统化分析,得出一系列结论;
- 提出一种语言引导的 FPN 框架,在语言的引导下通过执行跨尺度的信息融合来提升定位性能;
- 大量实验表明 LG-FPN 效果很好。
三、相关工作
A、参考表达式理解
两阶段方法和单阶段方法介绍。本文主要关注跨模态任务中多尺度特征的融合以及 neck 的作用。
B、特征金字塔
一般的 FPN 构建思路,典型例子:BFP、NAS-FPN。本文引入一种跨模态 FPN 结构,通过语言的引导自适应地整合高低水平的多模态特征。
四、初步的模型
这一部分主要用实验回答上面提出的两个问题:对于 REC 而言,多尺度的特征整合是否有益?目标检测领域的离线 neck 是否合适?
于是构建一个单阶段模型,组成:编码器模块、融合模块、Neck、检测头。
A、编码器模块
图像 I ∈ R W × H × 3 I\in R^{W\times H\times3} I∈RW×H×3,参考句子 S ∈ { s t } t = 1 T S\in\{s_t\}^T_{t=1} S∈{st}t=1T,其中 s t s_t st 为第 t t t 个单词, W × H × 3 {W\times H\times3} W×H×3 为图像尺寸,baseline 模型旨在找到图像 I I I 中的一个区域 I S I_S IS,从而对应 S S S 中的语义信息。
1、语言编码器
采用未级联的 BERT 作为语言编码器:首先将句子映射到相应的词 embedding 向量,之后和位置索引一起送入语言编码器,然后通过单层全连接层将每个句子维度变为 d = 256 d=256 d=256,得到词水平特征 E ∈ { e t } t = 1 T E\in\{e_t\}^T_{t=1} E∈{et}t=1T,其中 e t ∈ R d e_t\in R^d et∈Rd, T = 20 T=20 T=20。
2、图像编码器
采用 ResNet-101 作为 Backbone 提取视觉特征,输入图像尺寸 3 × 640 × 640 3\times640\times640 3×640×640,输出 Stage-3,4,5 的特征,分别为 V ^ 3 [ H 3 ∗ W 3 ∗ 512 ] \hat V_3 [H_3*W_3*512] V^3[H3∗W3∗512]、 V ^ 2 [ H 2 ∗ W 2 ∗ 1024 ] \hat V_2 [H_2*W_2*1024] V^2[H2∗W2∗1024]、 V ^ 1 [ H 1 ∗ W 1 ∗ 2048 ] \hat V_1 [H_1*W_1*2048] V^1[H1∗W1∗2048]。之后采用单层全连接层将其映射到维度 d = 256 d=256 d=256,从而得到视觉特征 V = { V i } i = 1 3 V=\{V_i\}^3_{i=1} V={Vi}i=13
B、融合模块
三种融合策略:FiLM、Transformer,前两者的联合。
1、融合策略1️⃣
FiLM 是一种通用的跨模态融合方法,采用逐特征的仿射变换来自适应地影响网络的输出,在 REC 中应用广泛。首先,FiLM 通过平均策略获取 E ∈ { e t } t = 1 T E\in\{e_t\}^T_{t=1} E∈{et}t=1T 的整体表达式特征 E F = 1 T ∑ t = 1 T e t E_F=\frac{1}{T}\sum_{t=1}^T e_t EF=T1∑t=1Tet,之后采用下列操作:
γ i = T a n h ( W i γ E F + b i γ ) β i = T a n h ( W i β E F + b j β ) F f i = R e L U ( C o n v ( R e L U ( γ i ⊙ V i ⊕ β i ) ) ) \begin{array}{l}\gamma_i=T a n h(W_i^\gamma E_F+b_i^\gamma)\\ \beta_i=T an h(W_i^\beta E_F+b_j^\beta)\\ F_f^i=Re LU(Conv(ReLU(\gamma_i\odot V_i\oplus\beta_i)))\end{array} γi=Tanh(WiγEF+biγ)βi=Tanh(WiβEF+bjβ)Ffi=ReLU(Conv(ReLU(γi⊙Vi⊕βi)))其中 W i γ W_i^\gamma Wiγ、 W i β W_i^\beta Wiβ、 b i γ b_i^\gamma biγ、 b j β b_j^\beta bjβ 为两个单层 MLP 的权重和偏执, T a n h T a n h Tanh 为激活函数, ⊙ \odot ⊙、 ⊕ \oplus ⊕ 表示逐元素的乘法和加法。最后,采用一个标准的 3 × 3 3\times3 3×3 卷积和 R e L U ReLU ReLU 操作产生多尺度的融合特征 F f = { F f i } i = 1 3 F_f=\{F_f^i\}^3_{i=1} Ff={Ffi}i=13, F f i ∈ R d × H i × W i F_f^i\in R^{d\times H_i\times W_i} Ffi∈Rd×Hi×Wi
2、融合策略2️⃣
仅采用 Vision-Guide-Language (VGL) 视觉引导语言模块来融合跨模态特征。具体来说,首先展平 V i V_i Vi 为 Z i = { Z s } s = 1 N i × d Z_i=\{Z_s\}^{N_i\times d}_{s=1} Zi={Zs}s=1Ni×d, N i = H i × W i N_i=H_i\times W_i Ni=Hi×Wi 为视觉 tokens 的数量。之后通过注意力机制计算 E E E 和 Z i Z_i Zi:
A i = softmax ( Q K T d ′ ) V Q = W i Q Z i , K = W i K E , V = W i V E A_i=\operatorname{softmax}(\dfrac{QK^\text{T}}{d'})V\\ Q=W_i^QZ_i,K=W_i^KE,V=W_i^VE Ai=softmax(d′QKT)VQ=WiQZi,K=WiKE,V=WiVE其中 W i Q W_i^Q WiQ、 W i K W_i^K WiK、 W i V W_i^V WiV 为 embedding 矩阵, d ′ = d / m d'=\sqrt{d/m} d′=d/m, m m m 为注意力头的数量。最终, A i A_i Ai 送入两个带有残差连接的 FFN。简单起见,每层视觉特征用一个 Transformer block 来进行融合,输出为 F t = { F t i } i = 1 3 F_t=\{F_t^i\}^3_{i=1} Ft={Fti}i=13, F t i ∈ R d × H i × W i F_t^i\in R^{d\times H_i\times W_i} Fti∈Rd×Hi×Wi。
2、融合策略3️⃣
策略1️⃣和策略2️⃣的联合。具体来说,首先在维度通道上拼接 F f F_f Ff 和 F t F_t Ft 得到 F f t ^ \hat{F_{ft}} Fft^,之后采用三个 1 × 1 1\times1 1×1 卷积层将 F f t ^ \hat{F_{ft}} Fft^ 的维度映射到 d d d,最后得到联合的特征 F f t = { F f t i } i = 1 3 F_{ft}=\{F_{ft}^i\}^3_{i=1} Fft={Ffti}i=13, F f t i ∈ R d × H i × W i F_{ft}^i\in R^{d\times H_i\times W_i} Ffti∈Rd×Hi×Wi。
C、Neck
现有的目标检测方法表明多尺度的特征融合有益于增强检测性能,但是在 REC 中性能有限。在 baseline 中,采用最简单的平均策略来建立跨尺度的交互。具体来说,给定多尺度的特征 F i F^i Fi,即 F f i F_f^i Ffi、 F t i F_t^i Fti、 F f t i F^i_{ft} Ffti,平均特征 F A V G F_{AVG} FAVG 计算如下:
F A V G = 1 3 ( u p s a m p l i n g ( F 1 ) + F 2 + d o w n s a m p l i n g ( F 3 ) ) F_{AVG}=\dfrac{1}{3}(upsampling(F^1)+F^2+downsampling(F^3)) FAVG=31(upsampling(F1)+F2+downsampling(F3)) 其中 u p s a m p l i n g upsampling upsampling、 d o w n s a m p l i n g downsampling downsampling 为双线性插值以及最大池化操作,将 F 1 F^1 F1、 F 3 F^3 F3 的分辨率调整为 F 2 F^2 F2, F A V G ∈ R d × H 2 × W 2 F_{AVG}\in R^{d\times H_2\times W_2} FAVG∈Rd×H2×W2。
D、检测头
首先采用 1 × 1 1\times1 1×1 卷积在 F A V G F_{AVG} FAVG 上将特征图尺度变换为 w × h × 5 w\times h\times5 w×h×5,其中 5 5 5 表示 5 个预测值 { t x , t y , t w , t h , t ^ } \{t_x,t_y,t_w,t_h,\hat t\} {tx,ty,tw,th,t^}, t x , t y t_x,t_y tx,ty 表示中心点的坐标, t w , t h t_w,t_h tw,th 为归一化的宽度和高度, t ^ \hat t t^ 为置信度,表示目标的一个中心点是否在该位置的概率。最后采用 cross-entropy 损失 L c l s L_{cls} Lcls 对中心点 t ^ \hat t t^, Mean Square Error (MSE) 损失 L o f f L_{off} Loff 对中心点的补偿 & 宽度和高度。同时采用 G I o U GIoU GIoU 作为辅助损失,整体损失函数如下:
L o s s = L c l s + λ o f f L o f f + L g i u Loss=L_{cls}+\lambda_{off}L_{off}+L_{giu} Loss=Lcls+λoffLoff+Lgiu其中 λ o f f = 5 \lambda_{off}=5 λoff=5。在推理时,选择最高得分的中心点来产生 bounding box。Intersection-over-Union (IoU) 作为评估指标,[email protected] 来衡量预测精度。
E、初步分析及结论
数据集:ReferItGame、ReferCOCO、RefCOCO+、RefCOCOg。
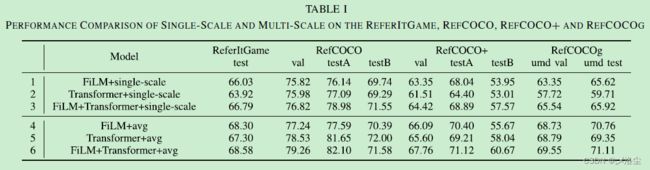
1、单尺度 vs. 多尺度
2、平均 vs. FPN
融合策略采用 FiLM+Transformer。
结论:之前的一些 FPN 结构不适合现在的 REC。
3、FPN 可视化分析
结论:目标检测需要获得高的召回率,而 REC 只需要定位到表达式对应的目标,FPN 结构会导致语义混乱。
五、提出的方法
由于语言中的语义能够隐含地揭示目标的颜色、形状、关系,于是设计模型无关的语言引导的 FPN 结构 language-guided FPN (LG-FPN)。主要是通过语言门和统一门动态地分配和选择细粒度的信息。编码器模块和融合模块与 baseline 相同,选取融合策略3️⃣得到多尺度特征 F = { F i } i = 1 3 F=\{F^i\}^3_{i=1} F={Fi}i=13。
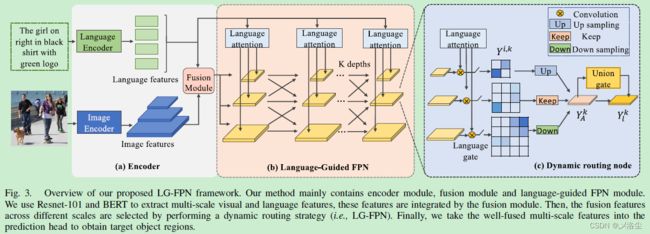
A、整体结构
建立深度为 K K K 的路径空间(级联结构),相邻阶段的尺度缩放因子为 2 2 2。输入由两部分组成:多尺度特征图和基于注意力机制的语言向量。之后在每个尺度上通过语言门选择难样本的网格信息。同时建立一个数据无关的统一门单元,进一步根据聚合的信息提炼网格。
B、语言门
图 3{c}:每一个路径节点 l l l 接收两类型的输入:多尺度特征图和语言向量。具体来说,对于语言编码器输出的语言 tokens E ∈ { e t } t = 1 T E\in\{e_t\}^T_{t=1} E∈{et}t=1T, e t ∈ R d e_t\in R^d et∈Rd,计算如下:
a k = s o f t m a x ( E W k ) e a k = ∑ i = 1 T a i k e i \begin{aligned}a^k=softmax(EW_k)\\ e_a^k=\sum_{i=1}^T a_i^ke_i\end{aligned} ak=softmax(EWk)eak=i=1∑Taikei其中 W k ∈ R d × 1 W_k\in R^{d\times 1} Wk∈Rd×1 为可学习的权重, k k k 表示深度,语言门 e a k e_a^k eak 在每个尺度和网格中共享。对于输入的多尺度图像特征 F i , k = { x s i , k } s = 1 N F^{i,k}=\{x_s^{i,k}\}^{N}_{s=1} Fi,k={xsi,k}s=1N,其中 i i i 为第 i i i 个尺度, k k k 为第 k k k 层, N = ( H i × W i ) N=(H_i\times W_i) N=(Hi×Wi)。之后通过 e a k e_a^k eak 动态选择网格特征 F i , k F^{i,k} Fi,k:
G i , k = σ ( e a k ∗ F i , k ) Y i , k = G i , k ⋅ c o n v 1 ( F i , k ) G^{i,k}=\sigma(e_a^k*F^{i,k})\\ Y^{i,k}=G^{i,k}\cdot conv_1(F^{i,k}) Gi,k=σ(eak∗Fi,k)Yi,k=Gi,k⋅conv1(Fi,k)其中 ∗ * ∗、 ⋅ \cdot ⋅ 表示卷积和 Hadamard 乘积。 c o n v 1 ( ⋅ ) conv_1(\cdot) conv1(⋅) 表示一个 3 × 3 3\times 3 3×3 卷积, σ ( ⋅ ) \sigma(\cdot) σ(⋅) 为激活函数。采用 m a x ( 0 , t a h n ( ⋅ ) ) ) max(0, tahn(\cdot))) max(0,tahn(⋅))) 作为门控转换器。输入为负,输出为 0 0 0。
C、统一门
对于语言门的输出 Y i , k Y^{i,k} Yi,k,通过上、下采样统一到同一分辨率下。用 Y A k Y_A^k YAk 表示语言门在节点 l l l 上聚合的特征。接下来通过数据独立门来精炼 Y A k Y_A^k YAk:
G l k = σ ( c o n v 2 ( Y A k ) ) Y l k = G s i , k ⋅ Y A k G_l^k=\sigma(conv_2(Y_A^k))\\ Y_l^k=G_s^{i,k}\cdot Y_A^k Glk=σ(conv2(YAk))Ylk=Gsi,k⋅YAk 其中 c o n v 2 ( ⋅ ) conv_2(\cdot) conv2(⋅) 为 1 × 1 1\times 1 1×1 卷积,将输出维度映射到单通道上。最后,在深度上堆叠来产生相应的 Bounding box。
六、实验
A、实验设置
1、数据集
ReferItGame、ReferCOCO、RefCOCO+、RefCOCOg。
2、实施细节
图像尺寸 640 × 640 640\times640 640×640,采用像素平均值填充,于是得到三个尺度的特征图 20 ∗ 20 ∗ 2048 20*20*2048 20∗20∗2048, 40 ∗ 40 ∗ 1024 40*40*1024 40∗40∗1024, 80 ∗ 80 ∗ 512 80*80*512 80∗80∗512,语言编码器为基础的 BERT,embedding 维度 768 768 768,总体维度 256 256 256,Adam 优化器,batch 8,head:8。单块 3090,20 epoch,初始学习率 1 e − 4 1e-4 1e−4,每 10 个 epochs 衰减一半,视觉、语言编码器的学习率为整体学习率的 1 / 10 1/10 1/10。
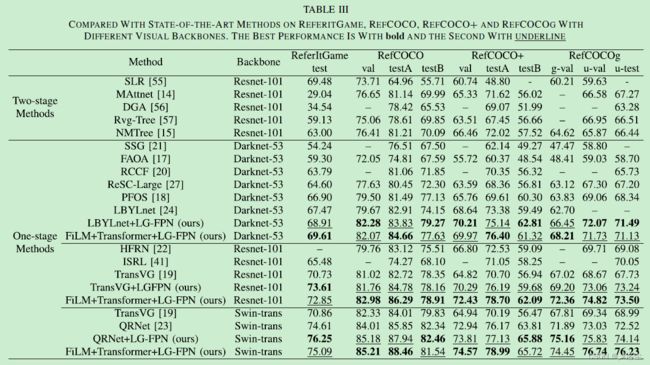
B、与不同 Backbones 的 SOTA 模型比较。
C、消融实验
在 ReferItGame 和 RefCOCOg 上进行。
1、融合策略
表 Ⅳ 1-4。
2、检测头
表 Ⅳ 5-9。
收敛曲线:
3、不同的细节
表 Ⅳ 10-12。
4、激活函数
表 Ⅳ 13-14。
5、不同的深度
七、定性结果
A、定性样本
B、可视化
八、结论
本文关注 REC 中的多尺度融合问题,现有的方法对 REC 任务的性能增强有限,于是提出一种模型无关的、语言引导的多尺度融合策略 LG-FPN,自适应地从低层和高层特征中选择关键的网格,并通过动态路径建立起跨尺度信息间的联系。实验效果很好。
写在后面
这篇文章创新点在于重新审视了 REC 中的多尺度融合机制,一针见血,实验充分,文笔也通俗,是篇好文章,缺点就是创新点还是没能够得上三大顶会的高度。