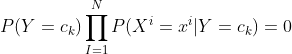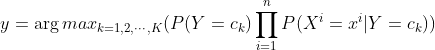Python机器学习：朴素贝叶斯

前两天不知道把书放哪去了，就停更了一下，昨天晚上发现被我放在书包夹层里面了，所以今天继续开始学习。

首先明确一下啊，朴素贝叶斯是什么：朴素贝叶斯分类器是一种有监督的统计学过滤器，在垃圾邮件过滤、信息检索等领域经常被使用到。

一、极大似然估计：这个我就不讲了，纯纯数理统计的问题，目标就是找到一个参数p，让他使得所有随机变量的联合概率最大，我就直接贴上一张图吧：

图1：最大似然估计

 二、朴素贝叶斯分类：

先回忆一下，概率论里面贝叶斯公式是什么？想不起来的话，建议翻一翻浙大的那本概率论与数理统计，那里面有的，简单的来说，就是求条件概率，或者说，已知道一件事情X发生的概率，求X发生情况下另一个事件Y发生的概率：

那么，用频率代替概率在样本集合上进行估计的话，就是：

三、拉普拉斯平滑：

如果说，我们的样本集合不够大，就可能没有法子去覆盖特征值的所有可能取值，也就是说，可能会出现这种情况：

这个时候，你不管怎么给其他的特征分量取值，都会出现：

这种情况，很麻烦吧，但是，这种情况是可以避免的，通过平滑处理（典型的就是拉普拉斯平滑）：

是的所有可能取值的个数。

来看一下书上给出的完整的朴素贝叶斯分类器的算法：

我们要输入的是:样本集合，待预测样本下，样本标记的所有可能值：样本输入变量X的每个属性的所有可能取值;

输出很简单：带预测样本x所属类别

算法如下：

step1：计算标记为的样本出现的概率：

step2：计算标记为的样本，其分量的属性值为的概率

step3：根据上面的估计值计算x属于所有的概率值，并且喧杂概率最大的作为输出

即：

 其实，朴素贝叶斯的本质就是极大似然估计，我也不知道再写些啥，书上有和的计算方法，想推的自己推一推吧，极大似然估计这个是考研数一的必考点，我在这里强烈推荐宇哥的视频，学完一身轻松。

我们看一个书上给出的利用朴素贝叶斯实现垃圾短信分类的应用，emm，他用的是SMS Spam Collection DataSet,you 5574条短信，其中有747条垃圾短信，数据集和是个纯文本，每行对应一条垃圾短信，第一个单词是Spam或者ham，表示是不是垃圾短信，这就是很简单的标签了，标签和短信内容之间用制表符分隔。

其实看到这个的时候，我想说，好好学一学，没啥坏处，我的qq邮箱和163邮箱里面全是垃圾邮件，每天都有，烦死了快。

找了一下啊，Kaggle上面是有这个数据集的，其他人的博客也给出了相关的下载地址，我会把这个传到我的下载哪一栏里面去，有需要的可以下载。

with open('./spam.csv','r',encoding='gb18030', errors='ignore')as f:
    sms=[line.split(',')for line in f ]#,encoding='utf-8'
y,x=zip(*sms)
from sklearn.feature_extraction.text import CountVectorizer as CV
from sklearn.model_selection import train_test_split
y=[label=='spam'for label in y]
x_train,x_test,y_train,y_test=train_test_split(x,y)
counter=CV(token_pattern='[a-zA-Z]{2,}')
x_train=counter.fit_transform(x_train)
x_test=counter.transform(x_test)
# print (x_train)
# print(x_test)
from sklearn.naive_bayes import MultinomialNB as NB
model=NB()
model.fit(x_train,y_train)
train_score=model.score(x_train,y_train)
test_score=model.score(x_test,y_test)
print("train_score:",train_score)
print("test_score:",test_score)

注意，这里有两个地方和书上的不一样，因为我从kaggle上面下载的是.csv文件，一直读不出来，然后查了一下，将encoding='utf-8'改成了encoding='gb18030', errors='ignore'，同时，这个数据集合并没有和书上说的那样子，标签和正文以空格隔开，而是用“，”隔开的，所以分隔那里我用的是

line.split(',')，这下才读取成功，这个地方告诉我们，搞之前要好好看一下数据集合，不能一昧的跟着书上走，因为书是先出的，你是后学的，先出的肯定会和你后面学习要用到的东西有出入，因地制宜，合理发展，产品迭代才是硬道理（此处连续三个/doge）

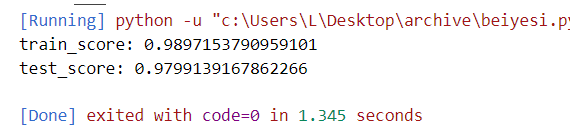
好了，来看看分类效果，为啥把两个print给注释了？没错误啊，绝对保真，就是输出太多了，我嫌烦才给注释了。

图2：朴素贝叶斯分类结果

 可以看到，训练结果是0.989，测试结果是0.979，效果还是可以滴。