2023.1.18-2022年蓝桥杯B组初赛题解
目录:
题目详解:
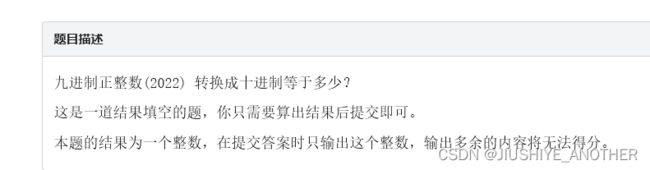
1、九进制转十进制
基础的填空题没什么好说的,就是进制转换
答案:1478
2、顺子日期
也是基础的填空题,不过这一题当时是有争议的。就是不知道012到底算不算顺子?我当时没算结果是4个,如果算上012的话,应该是14个。
答案:14
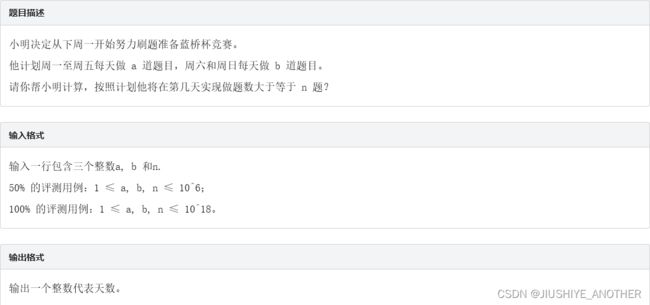
3、刷题统计
这题也没什么好说的,就是一道模拟题, 模拟一遍就可以得到答案不过我值得注意的是,这道题的范围很大。如果不进行处理的话,很容易超时。可以先算出每周可以做多少题,然后利用除法和取余,就能把取余后的做题量控制在一周内了
AC代码:
#include
using namespace std;
typedef long long ll;
ll a, b, n, k;
ll ans = 0;
int main() {
cin >> a >> b >> n;
k = a * 5 + b + b;
ans += n / k * 7;
n %= k;
if (n <= a * 5) {
ans += n / a + (n % a != 0);
}
else {
n -= a * 5;
ans += 6 + (n > b);
}
cout << ans << endl;
return 0;
}
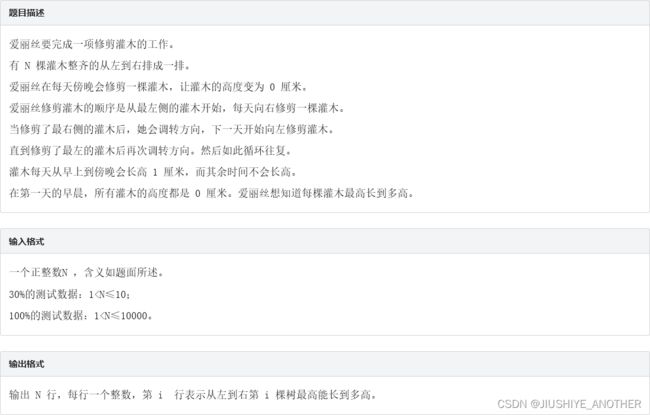
4、修剪灌木
这道题主要的关键在于看懂题目,看懂了他就只是一个贪心的题目。 对于每棵灌木,长到最高的时间段有两种可能:被剪后往右剪再拐回来,和被剪之后往左剪再拐回来假设某个灌木左侧有 x 棵灌木,右侧有 y 棵,容易发现这颗灌木的最大高度是 max(x, y) * 2,它的左(右)侧每有一颗灌木被剪前它都会长高 1 厘米,包括它自己被剪之前
AC代码:
#include
using namespace std;
int n;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
int x = max(i, n - i - 1);
cout << x * 2 << endl;
}
return 0;
}
5、X进制减法
这道题当时在做的时候没看了,题目比较长,先做后面的题目了。后来写完了转过头来想一想,发现题目的意思其实说的很明确。其实这题可以贪心出来答案。题目要求A-B的值最小,那我保证每一位进制都取尽可能的小就可以了。
AC代码:
#include
using namespace std;
typedef long long ll;
ll MOD = 1000000007;
int MAXM = 100005;
int n, ma, mb;
int a[MAXM], b[MAXM];
ll ans = 0, bac = 1;
int main() {
cin >> n;
cin >> ma;
for (int i = 0; i < ma; i++) {
cin >> a[i];
}
cin >> mb;
for (int i = 0; i < mb; i++) {
cin >> b[i];
}
int i = ma, j = mb;
while (i > 0) {
ans += (a[i] - b[j]) * bac;
ans %= MOD;
ll p = max(a[i], b[j]) + 1;
bac *= max(p, 2LL);
bac %= MOD;
i--;
if (j){
j--;
}
}
cout << ans << endl;
return 0;
}
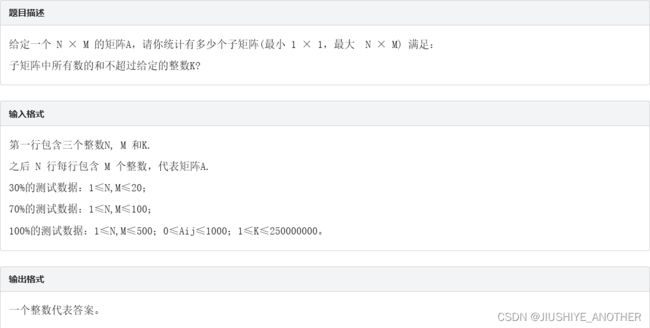
6、统计子矩阵
我去年主要是写了这一题,还有下面那道地雷扫描。 啊,现在虽然知道怎么做了,但是当时脑袋里面也想到了暴力搜索。虽然是知道有前缀和这个东西,但是还没有做过二维前缀和,当时没有准备充分()总而言之,这道题的知识点是二维前缀和降维加上一个连续子段的和。如果是暴力搜索的话,我记得当时在vj上面交的时候,暴力搜索是是过了三个点。
做法是先确定子矩阵的两个列边界,然后做一次行遍历,就是求符合条件的连续子段个数(双指针滑动窗口),复杂度缩小到 O(n^3)由于每次只需拿到某一行内的和相当于下降维度了,只做一维前缀和就行 (关于什么是二维前缀和)
AC代码:
#include
using namespace std;
typedef long long ll;
ll MOD = 1e9+7;
int N = 505;
ll m, n, k;
ll a[N][N];
ll ans = 0;
ll getsum(int i, int j, int x, int y) {
return a[x][y] - a[i - 1][y] - a[x][j - 1] + a[i - 1][j - 1];
}
int main() {
cin >> m >> n >> k;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j];
a[i][j] += a[i - 1][j] - a[i - 1][j - 1] + a[i][j - 1];
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (getsum(i, j, i, j) > k) continue;
for (int x = i; x <= m; x++) {
int l = j, r = n;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (getsum(i, j, x, mid) > k) r = mid - 1;
else l = mid;
}
if (getsum(i, j, x, l) > k) break;
ans += l - j + 1;
}
}
}
cout << ans << endl;
return 0;
}
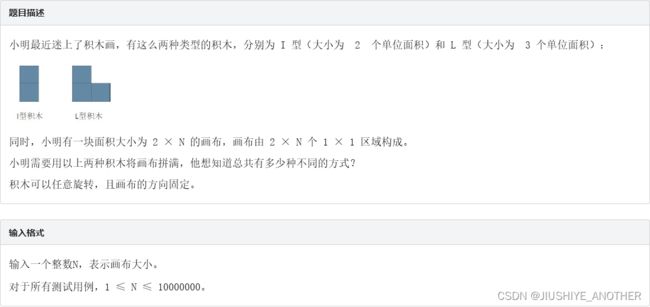
7、积木画
啊,就是dp,没什么好说的,要注意情况其实很多,不是只有样例那么一点()
AC代码:
#include
using namespace std;
typedef long long ll;
ll MOD = 1e9+7;
int N = 1e7+5;
int n;
ll dp[N];
int main() {
cin >> n;
dp[1] = 1;
dp[2] = 2;
dp[3] = 5;
for (int i = 4; i <= n; i++) {
dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % MOD;
}
cout << dp[n] << endl;
return 0;
}
8、扫雷
这一题是我过的点最多的一题(),题目的大概意思就是扫雷()他会发射一个引爆其他地雷的导弹。导弹和地雷都有爆炸半径。在爆炸后命中的半径中如果有雷同样也会爆炸。最后就看题目给定的导弹炸过之后最后一共炸了多少个地雷。当时的一个思路就是模拟爆炸的过程。当时用结构体储存一个雷的地点和数量。还有导弹也是,导弹就看成地雷。显然当时做这个题肯定是超时了()
AC代码:
#include
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
map,pair > mp;
map,int > vis;
int n,m;
int dfs_Trave(int x,int y,int r);
int dfs(pair,pair > index);
int main()
{
cin >> n >> m;
int x,y,r;
for(int i=0;iit->second.first)
{
auto val=make_pair(r,it->second.second+1);
mp[temp]=val;
}
else
{
auto val=make_pair(it->second.first,it->second.second+1);
mp[temp]=val;
}
}
}
int res=0;
for(int i=0;i>x >>y >> r;
res+=dfs_Trave(x,y,r);
}
cout << res << endl;
return 0;
}
int dfs(pair,pair > index)
{int x=index.first.first,y=index.first.second,r=index.second.first,num=index.second.second;
int sum=num;
vis[index.first]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
sum+=dfs(*it);
}
}
}
return sum;
}
int dfs_Trave(int x,int y,int r)
{
int sum=0;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
sum+=dfs(*it);
}
}
}
return sum;
}
9、李白打酒加强版
当时这道题看了一下,这个应该是dp,好,不会()
后来讲过之后知道了
#include
using namespace std;
int n,m;
int f[110][110][110][2];
const int M = 1000000007;
int main()
{
cin>>n>>m;
f[0][0][2][1]=1;
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<=101;k++)
{
for(int c=0;c<2;c++)
{
if(i > 0 && c == 1 && k % 2 == 0)
{
f[i][j][k][c] = (f[i - 1][j][k /2][0] + f[i - 1][j][k /2][1]) % M;
}
if(j > 0 && c == 0 && k >= 0)
{
f[i][j][k][c] = (f[i][j - 1][k+1][0] + f[i][j - 1][k +1][1]) % M;
}
}
}
}
}
cout< 10、砍竹子
1最后一题当时就完全没有看了。虽然现在知道是线段树,但还是没有思路。
AC代码:
#include
using namespace std;
typedef long long LL;
const int maxn=200010,m=10;
LL dp[maxn][m];
int main()
{
int n;
scanf("%d",&n);
LL sta[m],val,res=0;
int ans=0;
for(int i=0;i1) sta[++top]=val,val=sqrt(val/2+1);
ans=max(ans,top);
res+=top;
for(int j=0;top>0;++j,--top)
dp[i][j]=sta[top];
}
for(int i=0;i