数据结构之线性表，这一篇就够了，吐血总结，建议收藏~~

线性表及其顺序存储结构

三遍定律：
线性表有顺序存储结构和链式存储结构，本篇主要是顺序存储结构，链式存储结构请点击这里
线性表有顺序存储结构和链式存储结构，本篇主要是顺序存储结构，链式存储结构请点击这里
线性表有顺序存储结构和链式存储结构，本篇主要是顺序存储结构，链式存储结构请点击这里

痛定思痛，决定吐血总结一下线性表相关的知识，篇幅较多，字数较长，建议收藏学习！
另外，请大家多多指教！

又到了幼儿园放学的时间，今天天气很不错，光明顶幼儿园门口很多家长来接自己家的小宝贝，只见老师带着小朋友们，一个拉着另一个的衣服，依次从教室出来。而且我发现很有规律的是，每次他们的次序都是一样。比如宋远桥的儿子排在第5个，据说每次他都是在第5个，前面同样是那个小女孩，后面一直是那个小男孩。这点让我很奇怪，为什么一定要这样？

后来从老师那里得知，为了保障小朋友的安全，避免漏掉小朋友，所以给他们安排了出门的次序，事先规定好了，谁在谁的前面，谁在谁的后面。这样养成习惯后，如果有谁没有到位，他前面和后面的小朋友就会主动报告老师，某人不在。即使以后如果要外出到公园或博物馆等情况下，老师也可以很快地清点人数，万一有人走丢，也能在最快时间知道，及时去寻找。

我一想，还真是这样。小朋友们始终按照次序排队做事，出意外的情况就可能会少很多。毕竟，遵守秩序是文明的标志，应该从娃娃抓起。而且，真要有人丢失，小孩子反而是最认真负责的监督员。
再看看门外的这帮家长们，都挤在大门口，哪个分得清他们谁是谁呀。与小孩子们的井然有序形成了鲜明的对比。哎，有时大人的所作所为，其实还不如孩子。

好啦，不扯淡了，下面进入正题~~~

说明：文中的代码用了伪C代码

1.线性表的定义

线性表，顾名思义，是具有像线一样的性质的表。

线性表(List)：零个或多个数据元素的有限序列。

有几个关键的地方：首先它是一个序列，也就是说，元素之间是有顺序的，若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其他每个元素都有且只有一个前驱和后继。如果一个小朋友去拉两个小朋友后面的衣服，那就不可以排成一队了；同样，一个小朋友的衣服也不能被两个甚至更多小朋友拉；然后，线性表强调是有限的，小朋友班级人数是有限的，元素个数当然也是有限的。事实上，在计算机中处理的对象都是有限的，那种无限的数列，只存在于数学的概念中。

可用数学语言来进行定义，如下：

若将线性表记为（a1, … , ai-1, ai, ai+1, … , an），则表中 ai-1 领先于 ai，ai+1 领先于 ai，称 ai-1 是 ai 的直接前驱元素，ai+1 是 ai 的直接后继元素。当 i = 1,2, … , n-1 时，ai 有且仅有一个直接后继，当 i = 2,3, … , n 时，ai 有且仅有一个直接前驱。如图：

所以线性表元素的个数n（n≥0）定义为线性表的长度，当n=0时，称为空表。
在非空表中的每个数据元素都有一个确定的位置，如a1是第一个数据元素，an是最后一个数据元素，ai是第i个数据元素，称i为数据元素ai在线性表中的位序。

2.线性表的抽象数据类型

我们知道啦线性表的定义，在我们来分析一下，线性表应该有一些什么样的操作。

还是回到刚才幼儿园小朋友的例子，老师为了让小朋友有秩序地出入，所以就考虑给他们排一个队，并且是长期使用的顺序，这个考虑和安排的过程其实就是一个线性表的创建和初始化过程。

一开始没经验，把小朋友排好队后，发现有的高有的矮，队伍很难看，于是就让小朋友解散重新排——这是一个线性表重置为空表的操作。

排好了队，我们随时可以叫出队伍某一位置的小朋友名字及他的具体情况。比如有家长问，队伍里第五个孩子，怎么这么调皮，他叫什么名字呀，老师可以很快告诉这位家长，这就是宋远桥的儿子，叫宋青书。这种可以根据位序得到数据元素也是一种很重要的线性表操作。

还有什么呢，有时我们想知道，某个小朋友，比如郭靖是否是班里的小朋友，老师会说，不是，郭靖在桃花岛幼儿园里，不在我们幼儿园。这种查找某个元素是否存在的操作很常用。
而后有家长问老师，班里现在到底有多少个小朋友呀，这种获得线性表长度的问题也很普遍。
显然，对于一个幼儿园来说，加入一个新的小朋友到队列中，或因某个小朋友生病，需要移除某个位置，都是很正常的情况。对于一个线性表来说，插入数据和删除数据都是必须的操作。

所以，线性表的抽象数据类型定义如下：

ADT 线性表(List)
Data
线性表的数据对象集合为{a1, a2, …… ,an}，其中每个元素的类型均为DataType。
其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，
除了最后一个元素an外，每一个元素有且只有一个直接后继元素。
数据元素之间的关系是一对一的关系。
Operation
InitList(*L)： 初始化操作，建立一个空的线性表L。
ListEmpty(L)： 若线性表为空，返回true，否则返回false。
ClearList(*L)： 将线性表清空。
GetElem(L, i, *e): 将线性表L中的第 i 个位置元素值返回给e。
LocateElme(L, e)： 在线性表L中查找与给定值e相等的元素，
如果查找成功，返回该元素在表中序号表示成功；

来看一下下面这个操作，循环集合B中的每个元素，判断当前元素是否存在A中，若不存在，则插入到A中即可。

/* 将所有的在线性表 Lb 中但不在 La 中的数据元素插入到 La 中 */
void unionL(List *La, List Lb)
{
	int La_len, Lb_len, i;
	/* 声明与 La 和 Lb 相同的元素 e */
	ElemType e ;
	/* 求线性表的长度 */
	La_len = ListLength(*La);
	Lb_len = ListLength(Lb);
	for (i = 1; i <= Lb_len; i++)
	{
		/* 取 Lb 中第 i 个数据元素赋给 e */
		GetElem(Lb, i, &e);
		/* La 中不存在和 e 相同的数据元素 */
		if (!LocateElem(*La, e))
			/* 插入 */
			ListInsert(La, ++La_len, e);
		}
}

这里，我们对于union操作，用到了前面线性表基本操作ListLength、GetElem、LocateElem、ListInsert等，可见，对于复杂的个性化的操作，其实就是把基本操作组合起来实现的。

注意：当你传递一个参数给函数的时候，这个参数会不会在函数内被改动决定了使用什么参数形式。如果需要被改动，则需要传递指向这个参数的指针，如果不用被改动，可以直接传递这个参数。

3.线性表的顺序存储结构

顺序存储：线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素，是线性表的两种物理结构的一种。

线性表（a1,a2,…,an）的顺序存储示意图如下：

线性表的顺序存储结构，说白了，就是在内存中找了块地儿，通过占位的形式，把一定内存空间给占了，然后把相同数据类型的数据元素依次存放在这块空地中。既然线性表的每个数据元素的类型都相同，所以可以用C语言（其他语言也相同）的一维数组来实现顺序存储结构，即把第一个数据元素存到数组下标为0的位置中，接着把线性表相邻的元素存储在数组中相邻的位置。为了建立一个线性表，要在内存中找一块地，于是这块地的第一个位置就非常关键，它是存储空间的起始位置。

现实中也有这样的例子，在大学，一个宿舍八个人，小雨人特别老实、热心，我们时常会让他帮我们去图书馆占座，他总是答应，你想想，这其实明摆着是欺负人的事。他每次一吃完早饭就冲去图书馆，挑一个好地儿，把他书包里的书，一本一本地按座位放好，若书包里的书不够，他会把他的饭盒、水杯、水笔都用上，长长一排，九个座硬是被他占了。小雨同学占座时，如果图书馆里空座很多，他当然不必一定要选择第一排第一个位子，而是可以选择风水不错、美女较多的地儿。找到后，放一个书包在第一个位置，就表示从这开始，这地方暂时归我了。

接着，因为一共八个人，所以他需要占八个座。线性表中，我们估算这个线性表的最大存储容量，建立一个数组，数组的长度就是这个最大存储容量。

可实际上，一个宿舍总有那么几个不是很好学的人，为了游戏，为了恋爱，就不去图书馆自习了。假设我们八个人，去了六个，真正被使用的座位也就只是六个，另两个是空的。同样的，我们已经有了起始的位置，也有了最大的容量，于是我们可以在里面增加数据了。随着数据的插入，我们线性表的长度开始变大，不过线性表的当前长度不能超过存储容量，即数组的长度。想想也是，如果我们有九个人，只占了八个座，自然是坐不下的。

来看线性表的顺序存储的结构代码：

/* 存储空间初始分配量 */
#define MAXSIZE 20
/* ElemType类型根据实际情况而定，这里假设为int */
typedef int ElemType;
typedef struct
{
	/* 数组存储数据元素，最大值为MAXSIZE */
	ElemType data[MAXSIZE];
	/* 线性表当前长度 */
	int length;
} SqList;

顺序存储结构需要三个属性：

存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置。
线性表的最大存储容量：数组长度MaxSize。
线性表的当前长度：length.

注意：这里有两个概念“数组的长度”和“线性表的长度”需要区分一下。数组的长度是存放线性表的存储空间的长度，存储分配后这个量一般是不变的。有个别同学可能会问，数组的大小一定不可以变吗？我怎么看到有书中谈到可以动态分配的一维数组。是的，一般高级语言，比如C、VB、C++都可以用编程手段实现动态分配数组，不过这会带来性能上的损耗。线性表的长度是线性表中数据元素的个数，随着线性表插入和删除操作的进行，这个量是变化的。在任意时刻，线性表的长度应该小于等于数组的长度。

地址计算方法：

由于我们数数都是从1开始数的，线性表的定义也不能免俗，起始也是1，可C语言中的数组却是从0开始第一个下标的，于是线性表的第i个元素是要存储在数组下标为i-1的位置，即数据元素的序号和存放它的数组下标之间存在对应关系，如图：

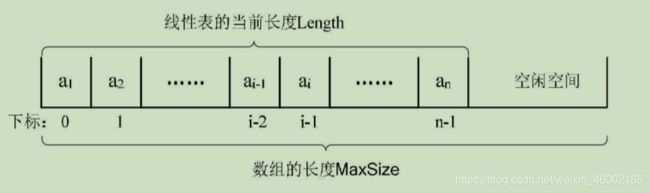
用数组存储顺序表意味着要分配固定长度的数组空间，由于线性表中可以进行插入和删除操作，因此分配的数组空间要大于等于当前线性表的长度。

其实，内存中的地址，就和图书馆或电影院里的座位一样，都是有编号的。存储器中的每个存储单元都有自己的编号，这个编号称为地址。当我们占座后，占座的第一个位置确定后，后面的位置都是可以计算的。试想一下，我是班级成绩第五名，我后面的10名同学成绩名次是多少呢？当然是6，7，…、15，因为5+1，5+2，…，5+10。由于每个数据元素，不管它是整型、实型还是字符型，它都是需要占用一定的存储单元空间的。假设占用的是c个存储单元，那么线性表中第i+1个数据元素的存储位置和第i个数据元素的存储位置满足下列关系（LOC表示获得存储位置的函数）：
LOC(ai+1)=LOC(ai)+c

所以对于第i个数据元素ai的存储位置可以由a1推算得出：
LOC(ai)=LOC(a1)+(i-1)*c

图解：

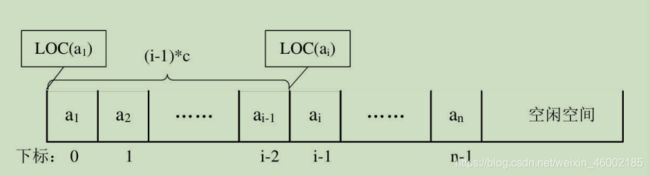
通过这个公式，你可以随时算出线性表中任意位置的地址，不管它是第一个还是最后一个，都是相同的时间。那么我们对每个线性表位置的存入或者取出数据，对于计算机来说都是相等的时间，也就是一个常数，因此用我们算法中学到的时间复杂度的概念来说(了解时间复杂度请点击这里)，它的存取时间性能为O(1)。我们通常把具有这一特点的存储结构称为随机存取结构。

4.顺序存储结构的插入与删除

(1) 获得元素操作

对于线性表的顺序存储结构来说，如果我们要实现GetElem操作，即将线性表L中的第i个位置元素值返回，其实是非常简单的。就程序而言，只要i的数值在数组下标范围内，就是把数组第i-1下标的值返回即可。来看代码：

#define OK 1
#define ERROR 0
#define TURE 1
#define FALSE 0
typedef int Status;
/* Status是函数的类型，其值是函数结果状态代码，如OK等 */
/* 初始条件：顺序线性表L已经存在，1 <= i <= ListLength(L) */
/* 操作结果：用e返回L中第 i 个数据元素的值 */
Status GetElem(SqList L, int i, ElemType *e)
{
	if (L.length == 0 || i < 1 || i > L.length)
		return ERROR;
	*e = L.data[i-1];
	return OK;
}

注意这里返回值类型Status是一个整型，返回OK代表1，ERROR代表0。下文代码相同。

(2) 插入操作

刚才我们也谈到，这里的时间复杂度为O(1)。我们现在来考虑，如果我们要实现ListIn-sert（*L,i,e），即在线性表L中的第i个位置插入新元素e，应该如何操作？

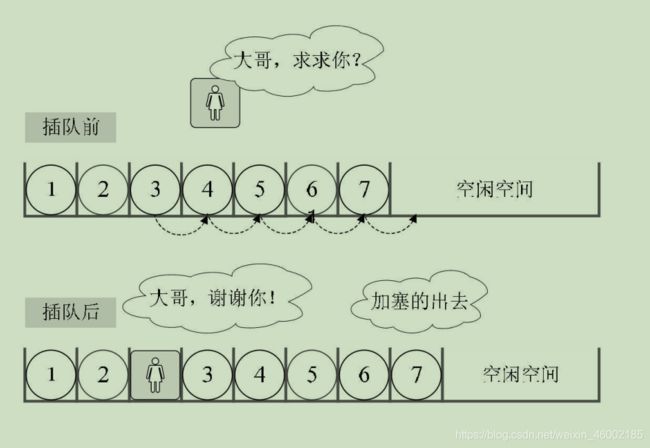
来看这样一个场景：我们在春运时去买火车票，大家都排队排的好好的。这时来了一个美女，对着队伍中排在第三位的你说，“大哥，求求你帮帮忙，我家母亲有病，我得急着回去看她，这队伍这么长，你可否让我排在你的前面？”你心一软，就同意了。这时，你必须得退后一步，否则她是没法进到队伍来的。这可不得了，后面的人像蠕虫一样，全部都得退一步。骂声四起。但后面的人也不清楚这加塞是怎么回事，没什么办法。

这个例子其实已经说明了线性表的顺序存储结构，在插入数据时的实现过程如下图所示：

来看下插入算法的思路：

如果插入位置不合理，抛出异常；
如果线性表长度大于等于数组长度，则抛出异常或动态增加容量；
从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置；
将要插入元素填入位置i处；
表长加一。

代码如下：

/* 初始条件：顺序线性表L已存在，1 <= i <= ListLength(L) */
/* 操作结果：在L中i个位置之前插入新的数据元素e，L的长度增加1 */
Status ListInsert(SqList *L,int i,ElemType e)
{
	int k;
	/* 顺序线性表已经满 */
	if (L->length == MAXSIZE)
		return ERROR;
	/* 当 i 不在范围内时 */
	if (i < 1 || i > L->length)
		return ERROR;
	/* 若插入数据位置不在表末尾 */
	if (i < L->length)
	{
		/* 将要插入位置后数据元素向后移动一位 */
		for (k = L->length - 1; k >= i - 1; k--)
			L->data[k+1] = L->data[k];
	}
	/* 将新元素插入 */
	L->data[i-1] = e;
	L->length++;
	return OK;
}

以上代码简洁明了，当然有兴趣的同学也可以用其他语言实现一下，加深理解。

(3)删除操作

接着刚才的例子。此时后面排队的人群意见都很大，人们都在抱怨咋还有人插队呢，服了。就在这时，远处跑来一胖子，对着这美女喊，可找到你了，你这骗子，还我钱。只见这女子二话不说，突然就冲出了队伍，胖子追在其后，消失在人群中。哦，原来她是倒卖火车票的黄牛，刚才还装可怜。于是排队的人群，又像蠕虫一样，均向前移动了一步，骂声渐息，队伍又恢复了平静。

线性表的顺序存储结构删除元素的过程，如下图：

删除算法的思路：

如果删除位置不合理，抛出异常；
取出删除元素；
从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置；
表长减1.

代码如下：

/* 初始条件：顺序线性表L已存在，1 ≤ i ≤ ListLength(L) */
/* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
Status ListDelete(SqList *L,int i,ElemType *e)
{
	int k;
	/* 线性表为空 */
	if (L->length == 0)
		return ERROR;
	/* 删除位置不正确 */
	if (i < 1 || i > L->length)
		return ERROR;
	*e = L->data[i-1];
	/* 如果删除的不是最后位置 */
	if (i < L->length)
	{
		/* 将删除位置后继元素前移 */
		for (k = i; k < L->length; k++)
			L->data[k-1] = L->data[k];
	}
	L->length--;
	return OK;

接下来我们分析一下插入和删除的时间复杂度。

先来看最好的情况，如果元素要插入到最后一个位置，或者删除最后一个元素，此时时间复杂度为O(1)，因为不需要移动元素，就如同一个人过来正常排队，当然是排在最后，如果此时他又不想排了，那么他一个人离开就行了，不影响任何人。

最坏情况：如果元素要插入或删除的元素位置是第一个，此时时间复杂度又是多少？那就意味着要移动所有的元素向后或者向前，时间复杂度为O(n)。

平均情况：由于元素插入到第 i 个位置，或删除第 i 个位置，需要移动 n-1 个元素。根据概率原理，每个位置插入或删除元素的可能性是相同的，也就是位置靠前，移动元素多，靠后，移动元素少。可以得到最终平均移动次数和最中间的那个元素的移动次数相等，为 (n-1)/2 。

根据时间复杂度的推导方法，可以得出，平均时间复杂度是 O(n) 。

我们思考一下：线性表的顺序存储结构，在存、读数据时，不管是哪个位置，时间复杂度都是O(1)；而插入或删除时，时间复杂度都是O(n)。这就说明，它比较适合元素个数不太变化，而更多是存取数据的应用。

(4)线性表顺序结构的优缺点

如图：