数据结构习题解析与实验指导-严蔚敏数据结构-第二章:线性表(刷题记录)
目录
第二章:线性表(刷题记录)P[18-20]
第一题:2022年4月7日 星期四 凌晨00:28 - 01:12
第二题:2022年4月7日 星期四 凌晨10:01 - 10:21
第三题:2022年4月7日 星期四 晚上23:21 - 23:31
第四题:2022年4月7日 星期四 晚上23:31 - 23:41
第五题:2022年4月8日 星期五 晚上19:10 - 19:20
第六题:2022年4月8日 星期五 晚上19:31 - 19:41
第七题:2022年4月9日 星期六 凌晨00:31 - 00:41
第八题:2022年4月9日 星期六 凌晨00:45 - 00:55
第九题:2022年4月9日 星期六 凌晨01:15 - 01:35
第十题:2022年4月9日 星期六 凌晨01:37 - 01:47
第十一题:2022年4月9日 星期六 下午14:47 - 14:57
第十二题:2022年4月9日 星期六 下午14:47 - 14:57
第十三题:2022年4月9日 星期六 下午15:21 - 15:44
第十四题:2022年4月10日 星期日 下午15:21 - 15:44
第十五题:2022年4月10日 星期日 晚上23:45 - 23:55
第十六题:2022年4月12日 星期二 晚上21:16 - 21:26
第十七题:2022年4月12日 星期二 晚上21:46 - 21:56(完结)
第二章:线性表(刷题记录)
P[18-20]

第一题:2022年4月7日 星期四 凌晨00:28 - 01:12
【算法思想】
要求利用现有的表中的结点空间建立新表,可通过更改结点的指针域来重新建立新的元素之间的线性关系。此题的关键点在于:为保证新表和原来一样递增有序,可以利用后插法建立单链表。
算法思想是:如图2.12所示,假设待合并的链表为La和Lb,合并后的新表使用头指针Lc(Lc的表头结点设为La的表头结点)指向。pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的首元结点。从首元结点开始进行比较,当两个链表La和Lb均未到达表尾结点时,依次摘取其中较小者重新链接在Lc表的最后。如果两个表中的元素相等,只摘取La表中的元素,删除Lb表中的元素,这样确保合并后的表中无重复的元素。当一个表到达表尾结点为空时,将非空表的剩余元素直接链接在Lc表的最后。最后释放链表Lb的头结点。
【算法描述】
void MergeList(LinkList &La, LinkList &Lb, LinkList &Lc)
{//将两个递增的有序链表La,Lb合并为一个递增的有序链表Lc
LinkList pa, pb, pc,q;
pa = La->next; //pa是链表La的工作指针,初始化为首元结点
pa = La->next; //pb是链表Lb的工作指针,初始化为首元结点
Lc = pc = La; //用La的头结点作为Lc的头结点
while (pa&&pb) //两个链表La,Lb均为到达表尾结点
{
if (pa->data < pb->data)
{//谁小谁先进Lc
pc->next = pa;
pc = pa;
pa = pa->next;
}
else if (pa->data > pb->data)
{
pc->next = pb;
pc = pb;
pb = pb->next;
}
else
{//相等时去=取La的元素,删除Lb的元素
pc->next = pa;
pc = pa;
pa = pa->next;
q = pb->next;
delete pb;
pb = q;
}
}
pc->next = pa ? pa:pb;
delete Lb;
}第二题:2022年4月7日 星期四 凌晨10:01 - 10:21
【算法思路】
与第1题类似的思路,从原有两个链表中依次摘取结点,通过更改结点的指针域来重新建立新的元素之间的线性关系,得到一个新链表。但与第1题不同的关键点有两个:(1)为保证新表与原表顺序相反,需要利用前插法建立单链表,而不能利用后插法;(2)当一个表到达表尾结点为空时,另一个非空表的剩余元素应该依次摘取,依次链接在Lc表的表头结点之后,而不能全部直接链接在Lc表的最后。
算法思想是:假设待合并的链表为La和Lb,合并后的新表使用头指针Lc(Lc的表头结点设为La的表头结点)指向。pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的首元结点。从首元结点开始进行比较,当两个链表La和Lb均为到达表尾结点时,依次摘取其中较小者重新链接在Lc表的表头结点之后,如果两个表中的元素相等,只摘取La表中的元素,保留Lb表中的元素。当一个表到达表尾结点为空时,将非空表的剩余元素依次摘取,链接在Lc表的表头结点之后。最后释放链表Lb的头结点。
【算法描述】
void MergeListplus(LinkList& La, LinkList& Lb, LinkList& Lc)
{//将两个非递减的有序链表La,Lb合并为一个非递增的有序链表Lc
LinkList pa, pb, pc, q;
pa = La->next; //pa是链表La的工作指针,初始化为首元结点
pa = La->next; //pb是链表Lb的工作指针,初始化为首元结点
Lc = pc = La; //用La的头结点作为Lc的头结点
Lc->next = NULL;
while (pa || pb) //只要有一个表未到达表尾结点,用Q指向待摘取的元素
{
if (!pa) //La为空,q指向pb,pb指针后移
{
q = pb;
pb = pb->next;
}
else if (!pb) //Lb为空,q指向pa,pa指针后移
{
q = pa;
pa = pa->next;
}
else if (pa->data <= pb->data)
{ //取较小者La中的元素,用q指向pa,pa指针后移
q = pa;
pa = pa->next;
}
else
{ //取较小者Lb中的元素,用q指向pb,pb指针后移
q = pb;
pb = pb->next;
}
q->next = Lc->next; Lc->next = q; //将q指向的结点插在Lc的表头结点之后0
}
delete Lb;
}
第三题:2022年4月7日 星期四 晚上23:21 - 23:31
【算法思路】
A与B的交集是指同时出现在两个集合中的元素,因此,此题的关键点在于:依次摘取两个表中相等的元素重新进行链接,删除其他不等的元素。
算法思想是:假设待合并的链表为La和Lb,合并后的新表使用头指针Lc(Lc的表头结点设为La的表头结点)指向。pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的首元结点。从首元结点开始进行比较,当两个链表La和Lb均为到达表尾结点时,如果两个表中的元素相等,摘取La表中的元素,删除Lb表中的元素;如果其中一个表中的元素较小,删除此表中较小的元素,此表的工作指针后移。当链表La和Lb有一个到达表尾结点为空时,依次删除另一个非空表中的所有元素。最后释放链表Lb的头结点。
【算法描述】
void InterSection(LinkList& La, LinkList& Lb, LinkList& Lc)
{//求两个递增的有序链表La,Lb的交集,使用头指针Lc指向
LinkList pa, pb, pc, u;
Initial(pa); Initial(pb); Initial(pc); Initial(u);
pa = La->next; //pa是链表La的工作指针,初始化为首元结点
pa = La->next; //pb是链表Lb的工作指针,初始化为首元结点
Lc = pc = La; //用La的头结点作为Lc的头结点
while (pa && pb) //两个链表La,Lb均为到达表尾结点
{
if (pa->data == pb->data) //相等,交际并入结果表中
{
pc->next = pa;
pc = pa;
pa = pa->next; //取La中的元素,将La链接在pc的后面,pa指针后移
u = pb;
pb = pb->next;
delete u; //删除Lb中的对应的相等元素
}
else if(pa->data < pb->data)//删除较小者La中的元素
{
u = pa;
pa = pa->next;
delete u;
}
else
{
u = pb;
pb = pb->next;
delete u;
}
}
while (pa) //Lb为空,删除非空表La中的所有元素
{
u = pa;
pa = pa->next;
delete u;
}
while (pb) //La为空,删除非空表Lb中的所有元素
{
u = pb;
pb = pb->next;
delete u;
}
pc->next = NULL; //置链表Lc尾标记
delete Lb; //释放Lc的头结点
}
第四题:2022年4月7日 星期四 晚上23:31 - 23:41
【算法思想】
求两个集合A和B的差集是指在A中删除A和B中共有的元素,即删除链表中的数据域相等的结点。由于要删除结点,此题的关键点在于:在遍历链表时,需要保存待删除结点的前驱。
算法思想是:假设待求的链表为La和Lb,pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的首元结点。pre为La中pa所指结点的前驱结点的指针,初始化为La。从首元结点开始进行比较,当两个链表La和Lb均未到达表尾结点时,如果La表中的元素小于Lb表中的元素,La表中的元素即为待求差集中的元素,差集元素个数增1,pre置为La表的工作指针pa,pa后移;如果Lb表中的元素小于La表中的元素,pb后移;如果La表中的元素等于Lb表中的元素,则在La表删除该元素值对应的结点。
【算法描述】
void Difference(LinkList& La, LinkList& Lb, int &n)
{//两个递增的有序链表La,Lb的差集存在La中,n是结果集合中的元素个数,调用时为0
LinkList pa, pb, u,q;
Initial(pa); Initial(pb); Initial(u); Initial(q);
pa = La->next; //pa是链表La的工作指针,初始化为首元结点
pa = La->next; //pb是链表Lb的工作指针,初始化为首元结点
u= La; //u作为La的中pa所指结点的前驱结点的指针
while (pa && pb) //两个链表La,Lb均为到达表尾结点
{
if (pa->data < pb->data) //A链表中当前结点指针后移
{
n++;
u = pa;
pa = pa->next;
}
else if (pa->data > pb->data)//B链表中当前结点指针后移
{
pb = pb->next;
}
else
{
u->next = pa->next;
q = pa;
pa = pa->next;
delete q; //删除结点
}
}
}第五题:2022年4月8日 星期五 晚上19:10 - 19:20
【算法思想】
题目要求将一个单链表A分解为两个具有相同结构的链表B、C,因此,此题的关键点在于:(1)B表的头结点可以使用原来A表的头结点,而需要为C表新申请一个头结点;(2)对A表进行遍历的同时进行分解,完成结点的重新链接,在此过程中需要记录遍历的后继结点以防止链接后丢失后继结点;(3)本题并未要求链表中结点的数据值有序,所以在摘取满足条件的结点进行链接时,可以采取前插法,也可以采取后插法。因为前插法的实现相对简单,下面的算法描述中采取了前插法。
算法思想是:首先将B表的头结点初始化A表的头结点,为C表新申请一个头结点,初始化为空表。从A表的首元结点开始,依次对A表进行遍历。p为工作指针,r为p的后继指针。当p>data<0时,将p指向的结点使用前插法插入到B表;当pa->data>0时,将p指向的结点使用
前插法插入到C表,然后p指向新的待处理的结点(p=r)。
【算法描述】
void Decompose(LinkList& A, LinkList& B, LinkList& C)
{//单链表A分解为两个具有相同结构的链表B和C
LinkList p, r;
Initial(A); Initial(B); Initial(C); Initial(p); Initial(r);
B = A;
B->next = NULL; //B表初始化
C = new LNode; //为C申请结点空间
C->next = NULL; //C初始化为空表
p = A->next; //p为工作指针
while (p!=NULL) //两个链表La,Lb均为到达表尾结点
{
r = p->next; //暂存p的后继
if (p->data < 0) //将小于0的结点链入B表中,前插法
{
p->next = B->next;
B->next = p;
}
else //将大于0的结点链入C表中,前插法
{
p->next = C->next;
C->next = p;
}
p = r; //p指向新的待处理结点
}
}第六题:2022年4月8日 星期五 晚上19:31 - 19:41
【算法思想】
此题的关键点在于:在遍历的时候利用指针pmax记录值最大的结点的位置。
算法思想是:初始时指针pmax指向首元结点,然后在遍历过程中,用pmax依次和后面的结点进行比较,发现大者则用pmax指向该结点。这样将链表从头到尾遍历一遍时,pmax所指向的结点中的数据即为最大值。
【算法描述】
ElemType Max(LinkList L)
{//确认单链表L中值最大的结点
LinkList p, pmax;
Initial(L); Initial(p); Initial(pmax);
pmax = L->next; //pmax指向首元结点
p = L->next->next; //p指向第二个结点
while (p != NULL) //遍历链表,如果下一个结点存在
{
if (p->data > pmax->data) //将小于0的结点链入B表中,前插法
{
pmax = p; //pmax指向数值大的结点
}
p = p->next; //p指向下一个结点,继续遍历
}
return pmax->data;
}第七题:2022年4月9日 星期六 凌晨00:31 - 00:41
【算法思想】
此题的关键点在于:不能开辟新的空间,只能改变指针的指向。因此,可以考虑逐个摘取结点,利用前插法创建链表的思想,将结点依次插到头结点的后面。因为先插入的结点为表尾,后插入的结点为表头,即可实现链表的逆转。
算法思想是:利用原有的头结点L,p为工作指针,初始时p指向首元结点。因为摘取的结点依次向前插入,为确保链表尾部为空,初始时应将头结点的指针域置为空。然后从前向后遍历链表,依次摘取结点,在摘取结点前需要用指针q记录后继结点,以防止链接后丢失后继结点,之后将摘取的结点插入到头结点的后面,最后p指向新的待处理的结点(p=q)。
【算法描述】
//7
void Inverse(LinkList &L)
{//逆置带头结点的单链表L
LinkList p, q;
Initial(L); Initial(p); Initial(q);
p = L->next; //p指向首元结点,p是工作指针啊
L->next = NULL; //头结点的指针域置为空
while (p != NULL) //遍历链表,如果下一个结点存在
{
q = p->next; //q指向*p的后继
p->next = L->next;
L->next = p; //*p插入在头结点之后
p = q;
}
}第八题:2022年4月9日 星期六 凌晨00:45 - 00:55
【算法思想】
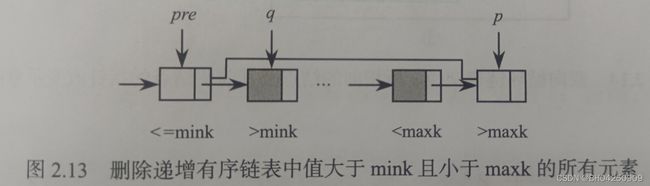
此题的关键点在于:通过遍历链表能够定位待删除元素的下边界和上边界,即可找到第一个值大于mink的结点和第一个值大于等于maxk的结点,分别如图2.13所示指针q和p指向的两个结点。
算法思想是:(1)查找第一个值大于mink的结点,用q指向该结点,pre指向该结点的前驱结点;(2)继续向下遍历链表,查找第一个值大于等于maxk的结点,用p指向该结点;(3)修改下边界前驱结点的指针域,使其指向上边界(pre->next=p);(4)依次释放待删除结点的空间(图中介于pre和p之间所有的结点)。
【算法描述】
//8
void DeleteMinMax(LinkList& L,int mink,int maxk)
{//删除递增有序链表L中值大于mink小于maxk的所有元素
LinkList p, q, pre, s;
Initial(L); Initial(p); Initial(q); Initial(pre); Initial(s);
p = L->next; //p指向首元结点,p是工作指针啊
while (p && p->data<=mink) //查找第一个值大于Mink的结点
{
pre = p; //pre指向前驱结点
p = p->next;
}
while (p && p->data < maxk) //查找第一个值大于等于maxk的结点
{
p = p->next;
q = pre->next;
pre->next = p; //修改待删除结点的指针
while (q != p)
{
s = q->next;
delete q;
q = s;
}
}
}第九题:2022年4月9日 星期六 凌晨01:15 - 01:35
【算法思想】
此题的关键点在于:双向循环链表的一个结点与前驱交换将涉及四个结点(结点*p,前驱结点*q,*q的前驱结点,*p的后继结点),如图2.14所示,总计需要改变六条链(结点*p的前驱指针和后继指针、结点*q的前驱指针和后继指针、结点*q的前驱结点的后继指针、结点*p的后继结点的前驱指针)。由于在改变指针前,需要用q指向结点*p的前驱结点,因此,在图2.14中,总计有七条指针的指向变化。
算法思想是:(1)用q指向结点*p的前驱结点;(2)结点*q的前驱结点的后继指针指向结点*p;(3)结点p的前驱指针指向结点*q的前驱结点;(4)结点*q的后继指针指向结点*p的后继结点;(5)结点*q的前驱指针指向结点*p;(6)结点p的后继结点的前驱指针指向q;(7)结点*p的后继指针指向结点*q。
//9
void Exchange(DuLinkList p)
{//在双向循环链表中,交换p所指向的结点及其前驱结点的顺序
DuLinkList q;
InitDuLinkList(&p); InitDuLinkList(&q);
q = p->next; //对应图2.14-步骤1
q->prior->next = p; //对应图2.14-步骤2
p->prior = q->prior; //对应图2.14-步骤3
q->next = p->next; //对应图2.14-步骤4
q->prior = p; //对应图2.14-步骤5
p->next->prior = q; //对应图2.14-步骤6
p->next = q; //对应图2.14-步骤7
}第十题:2022年4月9日 星期六 凌晨01:37 - 01:47
【算法思想】
此题的关键点在于:在时间复杂度为O(n)、空间复杂度为O(1)条件的限定下,不能另开辟空间,且只能通过遍历一趟顺序表来完成。
算法思想是:用k记录顺序表A中不等于item的元素个数,k初始为0。可以采用类似建立顺序表的思想,从前向后遍历顺序表,查找值不为item的元素,如果找到,则利用原表的空间记录值不为item的元素,同时使k增1。遍历结束后,顺序表中前k个元素即为值不为item的元素,最后将顺序表的长度置为k。
【算法描述】
//10
void DeleteItem(SqList &A,ElemType item)
{//删除顺序表A中所有值为item的元素
InitList_Sq(A);
int k = 0; //k记录值不等于item的元素个数
for (int i = 0; i < A.length; i++) //从前向后扫描顺序表
{
if (A.Elem[i] != item) //查找值不为item的元素
{
A.Elem[k] = A.Elem[i]; //利用原表空间记录值不为item的元素
k++; //不等于item的元素增1
}
}
A.length = k; //顺序表A的长度为k
}第十一题:2022年4月9日 星期六 下午14:47 - 14:57
(1)【算法思想】
定义指针p和q,初始化时均指向单链表的的首元结点。首先将p沿链表移动到第k个结点,而q指针保持不动,这样当p移动到第k+1个结点时,p和q所指结点的间隔距离为k。然后p和q同时向下移动,当p为NULL时,q所指向的结点就是该链表倒数第k个结点。
(2)【算法步骤】
①计数器i=0,用指针p和q指向首元结点。
②从首元结点开始依次顺着链域link依次向下遍历链表,若p为NULL,则转步骤⑤。
③若i小于k,则i加1;否则,q指向下一个结点。
④p指向下一个结点,转步骤②。
⑤若i等于k,则查找成功,输出该结点的data域的值,返回1;否则,查找失败,返回0。
(3)【算法描述】
//11
int Search_k(LinkList list, int k)
{//查找链表list中倒数第k个位置上的结点
LinkList p, q;
Initial(p); Initial(q);
int i = 0; //计数器赋初值
p = q = list->next; //p和q指向首元结点
while (p != NULL) //顺链域向后扫描,直到p为空
{
if (i < k)
{
i++; //计数器加1
}
else
{
q = q->next; //q移动到下一个结点
}
p = p->next; //p移动到下一个结点
}
if (i == k)
{
cout << q->data; //查找成功,输出该结点的data域的值
return 1;
}
else
{
return 0; //如果链表的长度小于k,查找失败
}
}第十二题:2022年4月9日 星期六 下午14:47 - 14:57
//12
void ReverseARRAY(int R[], int left, int right)
{//将数组R中的数据原地逆置
int i = left; int j = right;
while (i < j)
{
int temp = R[i];
R[i] = R[j];
R[j] = temp;
i++; //i右移一个位置
j--; //j左移一个位置
}
}
void LeftShift(int R[], int n, int p)
{//将长度为n的数组R中的数据左移p个位置
if (p > 0 && p < n)
{
ReverseARRAY(R, 0, n - 1); //将全部数据逆置
ReverseARRAY(R, 0, n - p - 1); //将前n-p个数据逆置
ReverseARRAY(R, n - p, n - 1); //将后p个元素逆置
}
}(3)【算法分析】
算法执行了三趟逆置,时间复杂度为O(n);用了一个辅助变量空间,空间复杂度为O(1)。
第十三题:2022年4月9日 星期六 下午15:21 - 15:44
(1)【算法思想】
分别求出序列A和B的中位数,设为a和b,算法具体求解过程如下:
①若a等于b,则a或b即为所求的中位数,算法结束;
②若a小于b,则舍弃序列A中较小的一半,同时舍弃序列B中较大的一半,且要求两次舍弃的元素个数相同;
③若a大于b,则舍弃序列A中较大的一半,同时舍弃序列B中较小的一半,且要求两次舍
弃的元素个数相同;
在保留的两个升序序列中,重复上述过程,直到两个序列中均只含一个元素时为止,较小者
即为所求的中位数。
(2)【算法描述】
//13
int Search_Mid(int A[], int B[], int n)
{//求两个长度均为n的序列A和B的中位数
int start1 = 0; int end1 = n - 1; //序列A的头、尾指针初始化
int start2 = 0; int end2 = n - 1; //序列B的头、尾指针初始化
while (start1 != end1 || start2 != end2)
{
int m1 = (start1 + end1) / 2;
int m2 = (start2 + end2) / 2;
if (A[m1] == B[m2]) //满足条件①,中位数相等,直接返回值
{
return A[m1];
}
else if (A[m1] < B[m2]) //满足条件②,a为较小中位数时
{//分别考虑奇数和偶数,保证两个子数组元素个数相等
if ((start1 + end1) % 2 == 0) //若元素为奇数个
{
start1 = m1; //舍弃A中间点以前部分且保留中间点
end2 = m2; //舍弃B中间点以后部分且保留中间点
}
else //若元素为偶数个
{
start1 = m1+1; //舍弃A的前半部分
end2 = m2; //舍弃B的后半部分
}
}
else //满足条件③,a为较大中位数时
{
if ((start1 + end1) % 2 == 0) //若元素为奇数个
{
end1 = m1; //舍弃A中间点以后部分且保留中间点
start2 = m2; //舍弃B中间点以前部分且保留中间点
}
else //若元素为偶数个
{
end1 = m1; //舍弃A的后半部分
start2 = m2 + 1; //舍弃B的前半部分
}
}
}
return A[start1] < B[start2] ? A[start1] : B[start2];
}(3)【算法分析】
算法时间复杂度为O(log2n),空间复杂度为O(1)。
第十四题:2022年4月10日 星期日 下午15:21 - 15:44
(1)【算法思想】
因为两个链表的长度不一定相同,所以当从头开始同时遍历两个链表到尾结点时,并不能保证两个链表同时到达尾结点。假设一个链表比另一个链表长k个结点,则可以先在较长的链表上遍历k个结点,之后同步从头遍历较短的链表,在遍历过程中,判断两个指针是否指向同一结点。若是,则该结点为共同后缀的起始位置。具体思路如下:
①分别求出链表str1和str2的长度,记为m和n。
②比较m和n,计算两个链表的长度之差k,k=|L1-L2|。令指针long指向较长链表的首元结点,指针short指向较短链表的首元结点。
③在较长的链表上遍历k个结点,这样将两个链表以表尾对齐,保证指针long和short所指的结点到表尾的长度相等。
④同步遍历两个链,反复将指针long和short同步向后移动,并判断它们是否指向同一结点。若long和short指向同一结点(通过比较结点的地址是否相等进行判断,而不是比较结点的值),则该结点即为所求的共同后缀的起始位置。
(2)【算法描述】
//14
typedef struct LNode
{
ElemType data;
struct LNode* next;
}LNode,*LinkList; //线性链表类型
LinkList FindSuffix(LinkList str1, LinkList str2)
{//求str1和str2所指的两个链表共同后缀的起始位置
LinkList p, q, longe, shorte;
Initial(p); Initial(q); Initial(longe); Initial(shorte);
p = str1->next; //p指向链表str1的首元结点
q = str2->next; //q指向链表str2的首元结点
int m=0, n=0, k=0 ;
while (p != NULL)
{
m++;
p = p->next; //求str1的长度,记为m
}
while (q != NULL)
{
n++;
q = q->next; //求str2的长度,记为n
}
if (m > n) //链表str1较长
{
longe = str1->next; //longe指向较长链表的首元结点
shorte = str2->next; //shorte指向较短链表的首元结点
k = m - n; //表长之差
}
else
{
longe = str2->next; //longe指向较长链表的首元结点
shorte = str1->next; //shorte指向较短链表的首元结点
k = n-m; //表长之差
}
while (k--)
{
longe = longe->next; //在较长链表上遍历k个结点
}
while (longe != NULL) //同步遍历两个链表,寻找共同后缀的起始位置
{
if (longe == shorte) //查找成功,返回共同后缀的起始位置
{
return longe;
}
else
{
longe = longe->next;
shorte = shorte->next;
}
}
return NULL; //查找失败
}(3)【算法分析】
算法时间复杂度为O(m+n)或O(max(m,n)),空间复杂度为O(1)。
第十五题:2022年4月10日 星期日 晚上23:45 - 23:55
(1)【算法思想】
主元素是数组中出现次数超过一半的元素。当数组中存在主元素时,所有非主元素的个数和必少于一半。如果让主元素与一个非主元素“配对”,则最后多出来的元素(没有元素与之配对)就是主元素。此题的关键点是:在主元素未知时,如何判断主元素并完成“配对”。具体思路如下。
①选取候选主元素:从前向后依次扫描数组中的每个整数,假定第一个整数为主元素,将其保存到Key中,计数为1;若遇到的下一个整数仍等于Key,则计数加1,否则计数减1。当计数减到0时,将遇到的下一个整数保存到Key中,计数重新记为1,开始新一轮计数,即从当前位置开始重复上述过程,直到将全部数组元素扫描完毕。
②判断Key中的元素是否是真正的主元素:再次扫描该数组,统计Key中元素出现的次数,若大于n/2,则为主元素,否则,序列中不存在主元素。
(2)【算法描述】
//15
int MainElement(int A[], int n)
{//求整数序列A的主元素
int count = 1 ,i; //count用来计数
int Key = A[0]; //Key用来保存候选主元素,初始为A[0]
for (i = 1; i < n; i++) //扫描数组,选取候选主元素
{
if (A[i] == Key)
{
count++; //候选主元素奇数加1
}
else
{
if (count > 0)
{
count--; //非候选主元素计数减1
}
else //更换候选主元素,重新计数
{
Key = A[i];
count = 1;
}
}
}
if (count > 0)
{
for (i = count = 0; i < n; i++)
{//统计候选主元素的实际次数
if (A[i] == Key)
{
count++;
}
}
}
if (count > n / 2)
{ //确认主元素
return Key;
}
else
{
return -1; //不存在主元素
}
}(3)【算法分析】
算法时间复杂度为O(n),空间复杂度为O(1)。
第十六题:2022年4月12日 星期二 晚上21:16 - 21:26
(1)【算法思想】
因为题目要求设计一个时间复杂度尽可能高效的算法,而已知|data|<=n,所以可以考虑用空间换时间的方法。申请一个空间大小为n+1(0号单元未用)的辅助数组,保存链表中已出现的数值,通过对链表进行一趟扫描来完成删除。具体思路如下:
①申请大小为n+1的辅助数组t并赋初值0;
②从首元结点开始遍历链表,依次检查t[data]]的值,若t[|datal]为0,即结点首次出现,则保留该结点,并置t[|datal]=1;若t[[data]不为0,则将该结点从链表中删除。
(2)单链表结点的数据类型定义如下:
typedef struct LNode
{
ElemType data;
struct LNode* next;
}LNode,*LinkList; //线性链表类型
(3)【算法描述】
//16
void DeleteEqualNode(LinkList head, int n)
{//删除单链表中绝对值相等的结点
int *t = new int[n + 1]; //辅助数组t,0号单元未用,故大小为n+1
for (int i = 0; i < n; i++) //数组初始元素置为0
{
*(t + i) = 0;
}
LinkList p = head->next; //p指向首元结点
LinkList r;
Initial(p); Initial(r);
while (p != NULL)
{
if (t[abs(p->data)] == 1) //此绝对值已经在结点中出现过,删除该结点
{
r->next = p->next;
delete p;
p = r->next;
}
else //未出现,删除该节点
{
t[abs(p->data)]=1; //将数组中对应位置的元素置为1
r = p;
p = p->next; //向后遍历链表
}
}
}(4)【算法分析】
对长度为m的链表进行一趟遍历,因此算法的时间复杂度为O(m);而申请空间大小为n+1
的辅助数组,因此空间复杂度为O(1)。
第十七题:2022年4月12日 星期二 晚上21:46 - 21:56(完结)
(1)【算法思想】
将最小的Ln/21个元素放在A:中,其余的元素放在Az中,划分结果即可满足要求。该算法并
不需要对全部元素进行全排序,可仿照快速排序的思想,基于枢轴将n个整数划分为两个子集。
根据划分后枢轴所处的位置i分以下三种情况处理:
①若[n/2」,则划分成功,算法结束;
②若[n/2」,则枢轴及之前的所有元素均属于A,继续对i之后的元素进行划分;
③若[n/2」,则枢轴及之后的所有元素均属于Az,继续对i之前的元素进行划分。
(2)【算法描述】
//17
int Partition(int a[], int n)
{//将正整数构成的集合划分为两个不相交的子集A1和A2
int low = 0, high = n - 1; //分别指向表的下界和上界
int low0 = 0, high0 = n - 1; //分别指向新的子表的下界和上界
int s1 = 0, s2 = 0; //分别记录A1和A2中元素的和
int flag = 1; //标记划分是否成功
int k = n / 2; //记录表的中间位置
while (flag) //循环进行划分
{
int pivotkey = a[low]; //选择枢轴
while (low < high) //从两端交替地向中间扫描
{
while (low < high && a[high] >= pivotkey)
{
--high; //从最右侧位置依次向左搜索
if (low != high)
a[low] = a[high]; //将比枢轴记录小的记录移到低端
while (low < high && a[low] <= pivotkey)
{
++low; //从最左侧位置依次向右搜索
}
if (low != high)
{
a[high] = a[low]; //将比枢轴记录大的记录移到高端
}
}
}//end of while(low
(3)【算法分析】
平均时间复杂度是O(n),空间复杂度是O(1)。