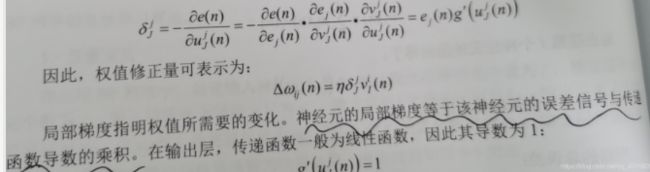bp神经网络,多输入多输出,3层网络matlab程序
1 项目背景
一个数据集,满足多对多 的对应关系。他希望用神经网络解决它的数据集逆问题。他给了我一个8输出,6输出的一个excel表格,前六列是输出后8列是输入。这样我利用matlab将表格导入为’.mat’文件。输入输出数据维度都在0-3范围。
或者做一个直接8-6的网络。前者就是多输入单输出,后者就是一个直接多对多的映射。
2神经网络
输入层节点数取决于输入向量长度
隐含层取决于数据集复杂程度,不宜过多不宜过少。
输出层,希望映射的数据节点。
学习率固定。
iteration+epoch,参数自定义
神经网络使用梯度下降算法
3数据集data.mat中的数据格式

前六列为输出数据,后8列为输出对应,一共950行。维度950*14;
4,数据处理
将数据先随机打乱,之后瓜分数据集,900训练,50测试。不进行归一化,直接输入。(如果要归一化,那么记得保存训练的均值和方差,在测试的时候需要使用。)
5 主要问题
1激活函数使用。我使用f=tanh(x)其中导函数f^ = (1-f^2).
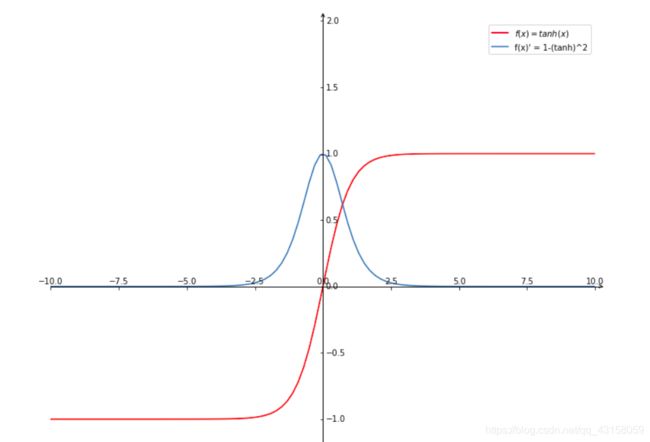
2输出层需要激活函数吗?
a输出层如果没设置非线性激活函数(tanh,sigmoid)。如果考虑到输出的数据大小,不在激活的范围值域内{-1-1},那么不需要激活函数。那么计算梯度的时候这一层就是线性的,计算梯度时候需要认为梯度是1。输出层是线性的方便在于,多元非线性拟合,或者数据预测时,不用反归一化。数据输出就是我们希望的目标数据。
并且求梯度的时候,方便了输出层的上一层。上一层隐含层输出的梯度计算
隐含层误差梯度=(输出层误差x激活函数导数) ,那么隐含层到输出层权值的变化量就是delat_w=学习率x隐含层误差梯度x隐含层输出,激活为线性的函数,那么导数为1.delat_W=学习率x输出误差x隐含层输出。这将大大简化编程和计算量。(利用神经网络的容错性。误差梯度不完全计算反向的非线性传导,按照权值矩阵分配有时候不失为一种好的方法,这就是为什么有些多层神经网络的隐含层层的误差梯度计算,有的是按照线性的误差传递)。
我试了一下按照线性误差比例反传梯度,和按照非线性激活函数反传的对比试验效果基本是一样的。()
b输出层设置非线性激活函数的时候,通常网络上常见的都是输出值域在(-1,1)或者是sigmoid的(0-1),,这时候我们需要计算他的反向传播的梯度。但是,但是,但是,我见过,使用了激活函数sigmoid输出,但是反传的时候。依旧按照线性梯度为1计算的,忽视梯度的变化,由于输出数据范围满足激活函数值域(0-1)。并且利用网络的容错性,可以实现线性传到输出到隐含层。只要隐含层网络中有非线性一个层就好,就可以实现收敛。当然如果非线性层多,那么就能够拟合更复杂的函数结构。
(那么全部按照线性传误差梯度,实现多层网络的非线性计算就变成了可能。神经网络神奇之处)
4 matlab神经网络主程序
%% 主函数
clear
Err_squ=[]
m=0; %迭代次数初始化定义
Err_record=[]; %每个数据的第一次迭代误差一共epoch*length(Y——train)个
MSE_train=[]; %mse 的每轮记录
Y_train_exp = []; %训练集实验结果
Y_test_exp = []; %测试集实验结果
%% 写数据
[X_train, Y_train ,X_test ,Y_test]= writeindata(900,50); %打乱数据输入,制作数据集
%% 神经网络参数定义
In=length(X_train(1,:)); %输入层神经元数当前6+4小时+平均
H=100;
Out=6; %输出层神经元数
w1=unifrnd(-1,1,In,H); %初始化的方式大小可修改,高斯分布,随机分布
w2=unifrnd(-1,1,H,Out); %随机初始化的范围可修改(-1,1) (-0.5 ,0.5) (0,1 )等等
Epoch=10; %数据集的重复次数代训练
Iteration=100; %一个batch训练迭代次数
Lr=0.001; %learning rate学习率%自适应学习率
%% 训练旧数据
while (m<=Epoch) % 外部的训练集epoch循环
m=m+1
for i=1:size(Y_train,1) % 串行训练从第一个数据开始
for j=1:Iteration % 每一个数据迭代的次数
%% 前向传播
In=X_train(i,:) ; %in的维度[1,8]
H_1i=In*w1; %h的维度[1,100] w1[8,100]
H_1o=tanh(H_1i);
outi=H_1o*w2;
outo=outi; %o的维度[1,6]
%误差函数E=1./2*(sum((Y_train(i)-outo).^2));
%% 反向传播
e=Y_train(i,:)-outo; %误差函数求导后的误差,符号与反向梯度合并,所以省略不写了。
Dout=e.*1;
Dh=(e*w2').*(1-H_1o.^2); %注意1matlab中(.*)是优先级高于*计算的.2(*)的顺序不应该改变(和矩阵维度行列的相乘有关)。
w2=w2+Lr*H_1o'*Dout; %权值变化=学习率x输入x误差梯度符号在求e时候合并,这里*的顺序很重要。
w1=w1+Lr*In'*Dh; %
if (j==1)
E=1./2*(sum((Y_train(i)-outo).^2));%记录每一个数据的第一次迭代时误差
Err_squ = [Err_squ E]; %记录数据集均方误差变化
end
end
end%进行一轮的迭代
%% %记录一代过程所有数据计算的均方误差画图
if(length(Err_squ)==length(Y_train))
MSE_train=[MSE_train sum(Err_squ)/length(Y_train)];%所有代的mse记录录
Err_squ=[];%MSE%误差矩阵 循环的归零
end
end
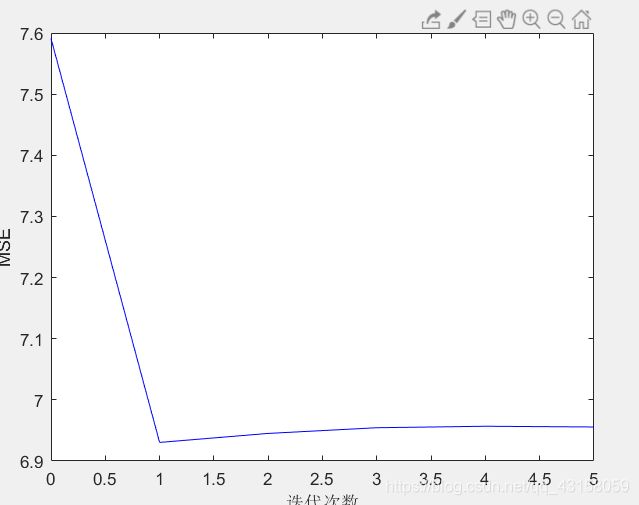
%% 画损失函数图(不有参考意义)
plotloss(MSE_train,'MSE',Epoch);%
%% 训练数据拟合
%[Y_train_exp,MSE_trainlast,R_square_train]=test1(w1,w2,w3,X_train,Y_train);
%plotc(Y_train(1:length(Y_train),:),Y_train_exp(1:length(Y_train),:),which,R_square_train,1);%1是变化坐标0是不变化坐标
%% 测试数据拟合
[Y_test_exp,MSE_train,R_square_test]=test2(w1,w2,X_test,Y_test);
for i=1:6
plotact(Y_test(:,i),Y_test_exp(:,i),i);
end
[a1,a2,a3,a4]=test2(w1,w2,X_test(2,:),Y_test(2,:))
string=['测试输出:',num2str(a1),'\n',' 实际对比: ',num2str(Y_test(2,:))]
string=['最小均方误差EMIN是:',num2str(min( MSE_train)),' r参数:',num2str(R_square_test)]
4matlab用到的程序函数
1自定义的数据集划分函数writeindata
2自定义的画图函数plotloss plotact
3自定义的测试函数test1,test2
5 测试集输出的拟合效果,前两个变量分别对应拟合。画出前两个输出拟合曲线,结果与希望对应。
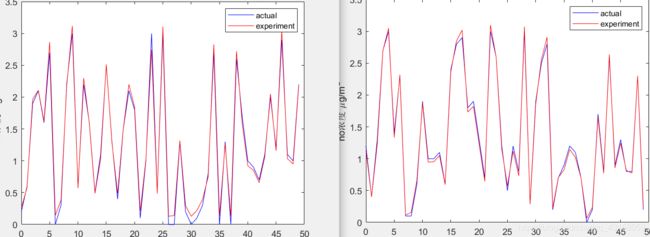
![]()
测试0.58对应0.6,0.400069对应0.4,0.04对应0.。精度可以达到1%甚至0.1%。
7 程序整体链接
https://download.csdn.net/download/qq_43158059/16720744