dp小结

CODEVS1253 超级市场

题目描述  Description

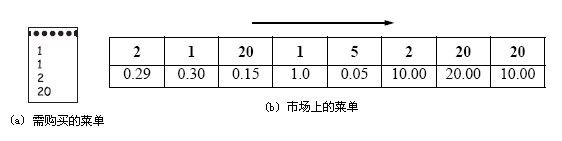
某人喜欢按照自己的规则去市场买菜，他每天都列一个买菜的清单，自由市场的菜码放也有一个顺序，该人有一个特点，就是按顺序买菜，从不走回头路，当然，她希望能花最好的钱买到所有的菜，你能帮帮他吗？

 

输入输出数据如下图：

 

思路：比较简单的dp，f[i][j]表示市场上的菜单到i需购买的菜单到j所需的最少花费，若i=j，则更新这个点，否则f[i][j]=f[i-1][j]。初始化将f[i][0]=0;其他都付最大值，最后比较f[n][m]和0x7fffffff，若大于则是impossible，否则输出。

 

 

 

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

struct use{

    int kind;

    double mon;

}b[100001];

double f[100001][101]={0};

int a[101]={0};

int main()

{

    int i,j,n,m,k;

    scanf("%d%d",&m,&n);

    memset(f,127,sizeof(f));

    for (i=1;i<=m;++i)

      scanf("%d",&a[i]);

    for (i=1;i<=n;++i)

      scanf("%d%lf",&b[i].kind,&b[i].mon);

    for(i=1;i<=n;++i)

      f[i][0]=0; 

    for (i=1;i<=n;++i)

      for (j=1;j<=m;++j)

      {

          f[i][j]=f[i-1][j];

        if (b[i].kind==a[j])

            f[i][j]=min(f[i][j],f[i-1][j-1]+b[i].mon);

      }

    if (f[n][m]>0x7fffffff) printf("Impossible\n");

    else

      printf("%.2f\n",f[n][m]);

}

RZUC Code

 

 

CODEVS1959 拔河游戏

题目描述  Description

一个学校举行拔河比赛，所有的人被分成了两组，每个人必须（且只能够）在其中的一组，要求两个组的人数相差不能超过1，且两个组内的所有人体重加起来尽可能地接近。

 

思路：一个二维费用（bool）背包问题，一个是元素个数（相当于体积），一个是体重。先求出总重的一半和元素个数一半，进行背包。

 

#include<iostream>

#include<cstdio>

using namespace std;

bool f[101][45001]={false};

int a[101]={0};

int main()

{

    int i,j,sum=0,n,k,q,cha,summ;

    cin>>n;

    if (n%2==0) k=n/2;

    else k=n/2+1;

    for (i=1;i<=n;++i)

    {

      cin>>a[i];

      sum+=a[i];

    }

    if (summ%2==0) summ=sum/2;

    else summ=sum/2+1;  

    for (i=0;i<=1;++i)

      f[i][0]=true;

    for (i=1;i<=n;++i)

      for (j=summ;j>=a[i];--j)

        for (q=k;q>=1;--q)

        f[q][j]=f[q][j]||f[q-1][j-a[i]];

    for (j=summ;j>=0;--j)

      if (f[k][j])

      {

          cout<<min(j,sum-j)<<" "<<max(j,sum-j)<<endl;

        break;

      }  

}

RZUC Code

 

 

CODEVS1060 搞笑世界杯

题目描述  Description

    随着世界杯小组赛的结束,法国,阿根廷等世界强队都纷纷被淘汰,让人心痛不已. 于是有

人组织了一场搞笑世界杯,将这些被淘汰的强队重新组织起来和世界杯一同比赛.你和你的朋

友欣然去购买球票.不过搞笑世界杯的球票出售方式也很特别,它们只准备了两种球票.A 类

票------免费球票 B 类票-------双倍价钱球票.购买时由工作人员通过掷硬币决定,投到正面

的买A类票, 反面的买B类票.并且由于是市场经济,主办方不可能倒贴钱,所以他们总是准备

了同样多的A类票和B类票.你和你的朋友十分幸运的排到了某场精彩比赛的最后两个位置.

这时工作人员开始通过硬币售票.不过更为幸运的是当工作人员到你们面前时他发现已无需

再掷硬币了,因为剩下的这两张票全是免费票。

 

    你和你的朋友在欣喜之余,想计算一下排在队尾的两个人同时拿到一种票的概率是多少

(包括同时拿A 类票或B类票) 假设工作人员准备了2n 张球票,其中n 张A类票,n 张B类票,并且排在队伍中的人每人必须且只能买一张球票(不管掷到的是该买A 还是该买B).

 

思路：先说一个比较坑爹的事情，读入的是2n，不是n。f[i][j]表示第i人买票时买了j张A票的概率。对于j有三种情况：

  1）j=0：f[i][j]=f[i-1][j]*0.5;   2)0<j<n:f[i][j]=(f[i-1][j]+f[i-1][j-1])*0.5;  3)j=n:f[i][j]=f[i-1][j]+f[i-1][j-1]*0.5。

初始化f[0][0]=1;输出f[n*2-2][n]*2(因为最后两张可以全是A或B);

 

#include<iostream>

#include<cstdio>

using namespace std;

double f[3000][3000]={0};

int main()

{

    int n,i,j;

    cin>>n;

    n/=2;

    f[0][0]=1;

    for (i=1;i<=2*n;++i)

      for (j=0;j<=n;++j)

      {

          if (j>i) continue;

          if (j==0) f[i][j]=f[i-1][j]*0.5;

          else

          {

              if (j<n) f[i][j]=(f[i-1][j]+f[i-1][j-1])*0.5;

              else f[i][j]=f[i-1][j]+f[i-1][j-1]*0.5;

          }

      }

    printf("%.4f\n",f[n*2-2][n]*2);

}

RZUC Code

 

 

CODEVS3369 膜拜

题目描述  Description

神牛有很多…当然…每个同学都有自己衷心膜拜的神牛.
某学校有两位神牛，神牛甲和神牛乙。新入学的N位同学们早已耳闻他们的神话。所以，已经衷心地膜拜其中一位了。
现在，老师要给他们分机房。
但是，要么保证整个机房都是同一位神牛的膜拜者，或者两个神牛的膜拜者人数差不超过M。
另外，现在N位同学排成一排，老师只会把连续一段的同学分进一个机房。老师想知道，至少需要多少个机房。

 

思路：预处理一下前i位置有多少个两个神牛的崇拜者（前缀和数组），然后就是dp部分了，f[i]表示分到i个人最少多少个教室，循环i和k（i-k表示最后一个教室的人数），更新f[i]的值。预处理：f[0]=0;

 

#include<iostream>

#include<cstdio>

#include<cstring>

#include<cmath>

using namespace std;

int f[3000]={0},sum1[3000]={0},sum2[3000]={0};

int main()

{

    int n,m,i,j,x;

    memset(f,127/3,sizeof(f));

    scanf("%d%d",&n,&m);

    for (i=1;i<=n;++i)

    {

      sum1[i]=sum1[i-1];

      sum2[i]=sum2[i-1];

      scanf("%d",&x);

      if (x==1) ++sum1[i];

      else ++sum2[i];

    }

    f[0]=0;

    for (i=1;i<=n;++i)

      for (j=0;j<i;++j)

        if (abs((sum1[i]-sum1[j])-(sum2[i]-sum2[j]))<=m||

           sum1[i]-sum1[j]==0||sum2[i]-sum2[j]==0)

          f[i]=min(f[i],f[j]+1);

    cout<<f[n]<<endl;

}

RZUC Code

 

 

CODEVS1491 取物品

题目描述  Description

现在有n个物品（有可能相同），请您编程计算从中取k个有多少种不同的取法。

 

思路：多重背包问题，将数字作为元素，出现的次数为个数。注意选取个数时候的循环要循环到1，一开始循环到了0，结果wa了。。。作死。。。

 

#include<iostream>

#include<cstdio>

#include<algorithm>

using namespace std;

int a[31],f[31]={0},w[31]={0};

int main()

{

    int n,k,i,j,p;

    cin>>n>>k;

    for (i=1;i<=n;++i)

      cin>>a[i];

    sort(a+1,a+n+1);

    ++w[0];

    ++w[w[0]];

    for (i=2;i<=n;++i)

    {

      if (a[i]==a[i-1])

        ++w[w[0]];

      else

      {

          ++w[0];

          ++w[w[0]];

      }

      if (w[w[0]]>k) w[w[0]]=k;

    }

    f[0]=1;

    for (i=1;i<=w[0];++i)

      for (j=k;j>=0;--j)

        for (p=w[i];p>=1;--p)

          if (j>=p)

            f[j]=f[j]+f[j-p];

    cout<<f[k]<<endl;

}

RZUC Code

 

 

小V1032

免费馅饼（NOI98）
　　SERKOI最新推出了一种叫做“免费馅饼”的游戏:游戏在一个舞台上进行。舞台的宽度为W格，天幕的高度为H格，游戏者占一格。开始时游戏者站在舞台的正中央，手里拿着一个托盘。下图为天幕的高度为4格时某一个时刻游戏者接馅饼的情景。
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。  
　　馅饼有很多种，游戏者事先根据自己的口味，对各种馅饼依次打了分。同时，在8-308电脑的遥控下，各种馅饼下落的速度也是不一样的，下落速度以格/秒为单位。 
　　当馅饼在某一秒末恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。
　　写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。
　　注意：同等情况下优先走编号小的点。

 

思路：二维数组f表示时间为i位置为j时最大的分数，way用来记录路径，输出的时候递归，比较麻烦。。。

 

 

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

int a[1500][1000]={0},f[1500][1000],way[1500][1000]={0};

void work(int t,int x)

{

    if (t>1) work(t-1,way[t][x]);

    cout<<x-way[t][x]<<endl;

}

int main()

{

    int w,h,i,j,k,x,t,p,v,e,maxt=0,mat,mai,man=0;

    cin>>w>>h;

    while (cin>>t>>x>>v>>p)

    {

        if ((h-1)%v==0) e=(h-1)/v+t;

        else e=(h-1)/v+t+1;

        a[e][x]=a[e][x]+p;

        if (e>maxt) maxt=e;

    }

    for (i=0;i<=1499;++i)

      for (j=0;j<=99;++j)

        f[i][j]=-1000000000; 

    f[0][w/2+1]=0;

    for (i=1;i<=maxt;++i)

      for (j=1;j<=w;++j)

        for (k=-2;k<=2;++k)

          if (j+k>=1&&j+k<=w)

          {

                if (f[i][j]<f[i-1][j+k]+a[i][j])

                {

                    f[i][j]=f[i-1][j+k]+a[i][j];

                    way[i][j]=j+k;

                }

          }

    for (i=1;i<=maxt;++i)

      for (j=1;j<=w;++j)

        if (f[i][j]>man)

        {

            man=f[i][j];

            mat=i;

            mai=j;

        }

    cout<<man<<endl; 

    if (man!=0) 

      work(mat,mai);

}

RZUC Code

 

 

小V1035邮局

一些村庄被建在一条笔直的高速公路边上。我们用一条坐标轴来描述这条高速公路，每一个村庄的坐标都是整数。没有两个村庄坐标相同。两个村庄间的距离，定义为它们坐标值差的绝对值。
人们需要在一些村庄建立邮局——当然，并不是每一个村庄都必须建立邮局。邮局必须被建在村庄里，因此它的坐标和它所在的村庄坐标相同。每个村庄使用离它最近的那个邮局，建立这些邮局的原则是：所有村庄到各自所使用的邮局的距离总和最小。
你的任务是编写一个程序，在给定了每个村庄的坐标和将要建立的邮局数之后，按照上述原则，合理地选择这些邮局的位置。

 

思路：a数组预处理i到j仅有一个邮局时的最小代价，f数组前i个村放j个邮局的最小代价，然后更新。。。最后又是输出方案。递归

 

#include<iostream>

#include<cstdio>

#include<cstring>

#include<cmath> 

using namespace std;

int a[500][500]={0},x[500]={0},f[500][100]={0},way[500][100]={0};

void work(int p,int q)

{

    if (q!=1) work(way[p][q],q-1);

    cout<<x[(way[p][q]+1+p)/2]<<" ";

}



int main()

{

    int i,j,k,n,m,mid;

    ios::sync_with_stdio(false);

    cin>>n>>m;

    memset(f,127/3,sizeof(f));

    for (i=1;i<=n;++i)

    {

      cin>>x[i];

    }

    for (i=1;i<=n-1;++i)

      for (j=i+1;j<=n;++j)

      {

            mid=(i+j)/2;

            for (k=i;k<=j;++k)

              a[i][j]=a[i][j]+abs(x[k]-x[mid]);

      }

    for (i=1;i<=n;++i)

      f[i][1]=a[1][i];

    for (j=2;j<=m;++j)

      for (i=j+1;i<=n;++i)

        for (k=j-1;k<=i-1;++k)

        {

            if (f[k][j-1]+a[k+1][i]<f[i][j])

            {

                f[i][j]=f[k][j-1]+a[k+1][i];

                way[i][j]=k;

            }

        }

    cout<<f[n][m]<<endl;

    work(n,m);

    cout<<endl;

}

RZUC Code

 

 

小V1080多人背包

DD 和好朋友们要去爬山啦！他们一共有 K 个人，每个人都会背一个包。这些包的容量是相同的，都是 V。可以装进背包里的一共有 N 种物品，每种物品都有给定的体积和价值。

在 DD 看来，合理的背包安排方案是这样的：

每个人背包里装的物品的总体积恰等于包的容量。 
每个包里的每种物品最多只有一件，但两个不同的包中可以存在相同的物品。 
任意两个人，他们包里的物品清单不能完全相同。 
在满足以上要求的前提下，所有包里的所有物品的总价值最大是多少呢？

 

思路：可以将k个人看做一个人，就是一个人前k优化方案，原来的一维背包变为二维的，表示体积为i的第j优解，用两个队列更新，每次选两个队列中较大的一个，放入f[i][j]。

 

#include<cstdio>

#include<iostream>

using namespace std;

int f[5001][51]={0},a[201]={0},w[201]={0},x,y,qx[51]={0},qy[51]={0};

int main()

{

    int k,v,n,i,j,t;

    long long ans=0;

    cin>>k>>v>>n;

    for (i=1;i<=n;++i)

      cin>>a[i]>>w[i];

    for (j=0;j<=v;++j)

      for (t=0;t<=k;++t)

        f[j][t]=-210000000;

    f[0][1]=0;

    for (i=1;i<=n;++i)

      for (j=v;j>=a[i];--j)

      {

         x=y=1;

         for (t=1;t<=k;++t)

         {

            qx[t]=f[j][t];

            qy[t]=f[j-a[i]][t];

         }

         for (t=1;t<=k;++t)

         {

              if (qx[x]==-210000000&&qy[y]==-210000000) break;

              f[j][t]=qx[x];

              ++x;

              if (qy[y]+w[i]>f[j][t])

              {

                --x;

                f[j][t]=qy[y]+w[i];

                ++y;

              }

         }

      }

    for (i=1;i<=k;++i)

      ans=ans+f[v][i];

    cout<<ans<<endl;

}

RZUC Code

 

HAOI2015树上染色

题目大意：给树上n个点染k个黑色，求黑点之间、白点之间距离和的最大值。

思路：感觉是树形dp，但是觉得转移的时候很难受。后来听到fye大神的背包，就开始想背包方向想，发现多重背包可以解决。我们dfs一个孩子之后就可以进行背包了。但是赋初值的时候，要给f[u][0]和f[u][1]都赋为0，因为对于u这个根节点，我们可以涂两种颜色，初始值中的f[u][0]表示把它涂成白色，而f[u][1]表示涂成黑色，其他都是-∞就可以了。

View Code

 

SCOI2008着色方案

题目大意：有k种不同的颜色，每种颜色有ci种，求相邻涂不同颜色的方案数。

思路：一开始并不知道该怎么写，后来在其他大神的讲解下，才注意到ci<=5，然后听说用六维数组，然后就开始写，发现挂了。。。又听了他们的讲解。发现动态转移中六个变量a、b、c、d、e、i，分别保存剩余一个、两个、三个……五个的染色种类数和上一个涂的颜色是1~5中的哪一个，因为是上一次的，所以我们在下一层比较的时候要-1。然后用记忆化搜索。f[a][b][c][d][e][i]=(a-(i==2))*f[a-1][b][c][d][e][1]+(b-(i==3))*f[a+1][b-1][c][d][e][2]+……e*f[a][b][c][d+1][e-1][5]。

#include<iostream>

#include<cstdio>

#include<cstring>

#define inf 1000000007

using namespace std;

long long f[16][16][16][16][16][6]={0};

int ci[16]={0},num[6]={0},k;

bool visit[16][16][16][16][16][6]={false};

long long dp(int a,int b,int c,int d,int e,int co)

{

    long long ans=0;

    int i;

    if (a<0||b<0||c<0||d<0||e<0) return 0;

    if (!a&&!b&&!c&&!d&&!e) return 1;

    if (visit[a][b][c][d][e][co]) return f[a][b][c][d][e][co];

    ans=(ans+(a-(co==2))*dp(a-1,b,c,d,e,1))%inf;

    ans=(ans+(b-(co==3))*dp(a+1,b-1,c,d,e,2))%inf;

    ans=(ans+(c-(co==4))*dp(a,b+1,c-1,d,e,3))%inf;

    ans=(ans+(d-(co==5))*dp(a,b,c+1,d-1,e,4))%inf;

    ans=(ans+e*dp(a,b,c,d+1,e-1,5))%inf;

    visit[a][b][c][d][e][co]=true;

    return f[a][b][c][d][e][co]=ans;

}

int main()

{

    int i,j;

    scanf("%d",&k);

    for (i=1;i<=k;++i) 

    {

       scanf("%d",&ci[i]);

       ++num[ci[i]];

    }

    printf("%lld\n",dp(num[1],num[2],num[3],num[4],num[5],0));

}

View Code

 

HAOI2007上升序列

题目大意：给定一个序列，求任意长度的上升子序列，要求字典序最小（这里的字典序是位置最小）

思路：用nlogn的做法求最长上升子序列，然后从头往后扫m遍，找后面的值大的同时f数组满足相应条件的值输出。求f数组的时候，用lower_bound wa了，但用upper_bound就ac了。。。

View Code

 

bzoj1019 SHOI汉诺塔

题目大意：给定移动优先级的汉诺塔游戏，求多少步走完。（AB表示从A移到B）

思路：一开始只会暴搜，但是n到30，肯定超时。后来才知道是dp。借鉴普通汉诺塔的思路，我们从一个柱子移到另一个，就是先移动i-1个，然后把最大的移走，然后再把这i-1个移到最大的上面。这里的优先级就要求我们可能要多移动几次柱子，从而满足要求。我们用fi[i][j]表示i上有j个圆盘移走的步数，gi[i][j]表示i上j个圆盘移到的柱子,a为当前的柱子，b为i-1个移到的柱子，c就是第三个柱子，c=3-a-b。我们分情况讨论一下：如果gi[b][i-1]=c，我们只需要把i-1个从a移到b，最大的一个从a上移走，然后把b上的i-1个移到c，这样最后移到了c；如果gi[b][i-1]=a，我们需要把i-1个从a移到b，最大的一个从a上移走，然后把i-1个从b移到a，把最大的一个从c移到b，然后把i-1个从a移到b上就可以了，这样最后移到了b。这样我们就可以写出dp了，同时初始化保证了每个柱子上的圆盘都是按优先级移动，之后的每一步都是满足优先级的。

这道题目题意很明确，同时有是常见模型汉诺塔问题的变化，值得反思。

#include<iostream>

#include<cstring>

#include<algorithm>

#include<cstdio>

#define maxnode 35

using namespace std;

int move[7][2]={0},gi[3][maxnode]={0};

long long fi[3][maxnode]={0};

int main()

{

    int n,i,j,a,b,c;

    char ch;

    scanf("%d",&n);

    for (i=1;i<=6;++i)

      for (j=0;j<=1;++j)

      {

          while(scanf("%c",&ch)==1){if (ch>='A'&&ch<='C') break;}

          move[i][j]=ch-'A';

      }

    for (i=0;i<3;++i)

      for (j=1;j<=6;++j)

          if (move[j][0]==i)

          {

              fi[i][1]=1;gi[i][1]=move[j][1];break;

          }

    for (i=2;i<=n;++i)

      for (a=0;a<3;++a)

      {

          b=gi[a][i-1];c=3-a-b;

          fi[a][i]=fi[a][i-1]+1;

          if (gi[b][i-1]==c)

          {

              fi[a][i]+=fi[b][i-1];gi[a][i]=c;

          }

          else

          {

              fi[a][i]+=fi[b][i-1]+1+fi[a][i-1];gi[a][i]=b;

          }

      }

    printf("%lld\n",fi[0][n]);

}

View Code