2023.04.02 学习周报

---

摘要

This week, I read a computer science related to sequential recommendation systems, this article aims to systematically study the impact of sequential recommendations; Discover two basic time patterns of user behavior: absolute time patterns and relative time patterns, where the former highlights user sensitive behavior, such as people often contacting specific products at a certain point in time, while the latter reflects the impact between the two behaviors in time intervals; In order to integrate this information into a unified model, a neural network model is designed, which combines these patterns to simulate the dynamic preferences of users; According to the experimental results, this model has significant performance improvements compared to the most advanced models. In addition, I learn the LaPlacian Eigenmaps algorithm, the ant colony algorithm, and the Navier-Stokes equation; Understand the Laplacian Eigenmaps algorithm through mathematical derivation and code implementation; Understand the use of ant colony algorithm by comparing it with polynomial time algorithm, and learn the basic knowledge of Navier-Stokes equations.

本周，我阅读了一篇与顺序推荐系统相关的文章，这篇文章旨在系统地研究顺序推荐的影响；发现用户行为的两个基本时间模式：绝对时间模式和相对时间模式，其中前者突出了用户敏感行为，例如人们经常在某个时间点与特定产品接触，而后者反映在时间间隔中两个行为之间的影响；为了将这些信息整合到一个统一的模型中，设计了一个神经网络模型，该模型将这些模式联合学习，以模拟用户的动态偏好；根据实验结果表明，该模型与最先进的模型相比，具有显著的性能提升。此外，我学习了LaPlacian Eigenmaps算法、蚁群算法和Navier-Stokes方程；通过数学推导和代码实现去理解LaPlacian Eigenmaps算法；通过与多项式时间算法相比，去了解蚁群算法的用途，以及学习了Navier-Stokes方程的基础知识。

---

文献阅读

1.题目

文献链接：Time Matters Sequential Recommendation with Complex Temporal Information

2.摘要

Incorporating temporal information into recommender systems has recently attracted increasing attention from both the industrial and academic research communities. Existing methods mostly reduce the temporal information of behaviors to behavior sequences for subsequently RNN-based modeling. In such a simple manner, crucial time-related signals have been largely neglected. This paper aims to systematically investigate the effects of the temporal information in sequential recommendations. In particular, we firstly discover two elementary temporal patterns of user behaviors: “absolute time patterns” and “relative time patterns”, where the former highlights user time-sensitive behaviors, e.g., people may frequently interact with specific products at certain time point, and the latter indicates how time interval influences the relationship between two actions. For seamlessly incorporating these information into a unified model, we devise a neural architecture that jointly learns those temporal patterns to model user dynamic preferences. Extensive experiments on real-world datasets demonstrate the superiority of our model, comparing with the state-of-the-arts.

3.简介

在研究中，作者系统地研究了顺序推荐中的时间信息：

1）推荐系统作为一种有效的信息过滤方法，已经被部署在许多实际应用中。例如，从视频共享网站、电子商务到在线书店和社交网络；
2）现有的顺序推荐算法大多关注用户的行为序列，而忽略了用户的时间模式；
3）传统的推荐系统通常使用概念漂移来对用户兴趣的时间演变进行建模，其中假设用户的兴趣随着时间的推移而平稳演变；
4）最近基于神经网络的方法，特别是基于会话的推荐，主要关注于跟踪短期用户兴趣，并且只将项目的顺序纳入建模；
5）尽管在将时间信息整合到顺序推荐中有一些初步的努力，但它们大多考虑了不完整的时间信息；
6）在对这种综合的时间模式进行全面彻底的建模方面仍然缺乏努力。

4.本文贡献

1）基于深入的数据分析，作者发现了绝对时间模式和相对时间模式，为推荐系统建模用户的时间行为；
2）文章提出了一种新的时间感知神经网络TASER，以独特的视角去利用这些时间模式；
3）在真实世界的数据集上进行了广泛的实验，以证明文章提出的模型与最先进的方法相比具有显著的性能提升。

5.PROBLEM FORMULATION

5.1 Case Study

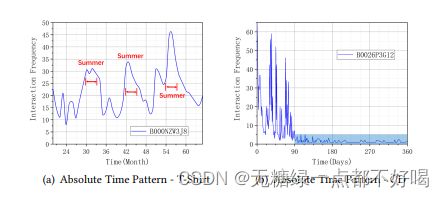
1）绝对时间模式
绝对时间模式是一个逐点概念，它将绝对时间戳描述为用户-项目交互的唯一变量；时间戳可以提供上下文和辅助信息，以确定用户是否对一个项目感兴趣，这在揭示周期行为方面很有用。

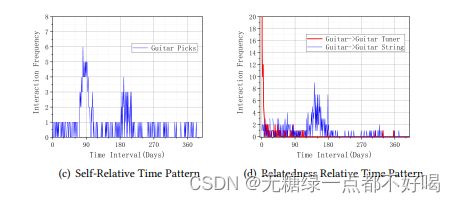
2）相对时间模式
相对时间模式是一个成对的概念，它关注每对用户行为之间的时间间隔；直观来讲，这样的信息反映了前一种行为对后一种行为的影响，不同的对可能表现出不同的模式；因此，作者进一步提出了两种相对时间模式：自我相对时间模式和关系相对时间模式。

5.2 Problem Definition

文章将矩阵、向量和标量分别表示为、和：
假设有一个用户集U和一个商品集i，对于用户∈U，按时间顺序组织她的购买行为 = [(1，1)，(2，2)…(,))，所有用户行为的集合定义为S ={|∈U}。给定U, I, S和目标时间戳，任务旨在预测每个用户的目标项，在时刻上的行为。

6.MODEL

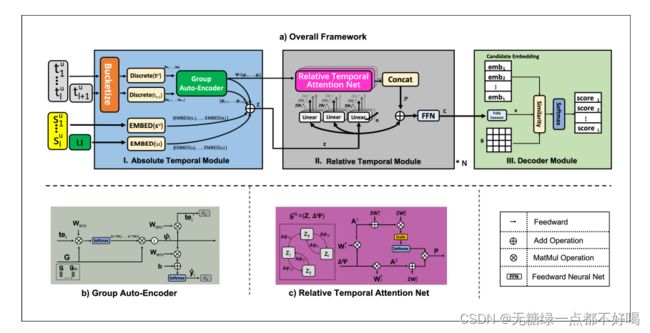
6.1 Absolute Temporal Module

绝对时间模块用于捕获绝对时间信息，该模块的输入包括四个组成部分:物品序列，对应的时间序列，目标用户和下一次交互时间+1，输出为=[1，2，…]：

其中：E(·)表示嵌入层，将离散变量直接编码为嵌入，将连续变量离散为离散值进行编码。

桶化的粒度可能有很大不同，不适当的桶化通常会导致性能较差；为了解决这个问题，将群自动编码器集成到这个模块中；群自动编码器的目标是将嵌入的时间编码为上的概率分布。

映射到th组的概率计算如下：

的群嵌入计算如下：

其中：可以被视为的高级表示。那么绝对时序嵌入模块的输出可以改写如下：

6.2 Relative Temporal Module

对于每个输入序列=[1，2，····，]，其中∈R是绝对时态模块输出的项目节点的嵌入；首先根据查询、键和相对时间计算注意系数矩阵∈R×，也就是注意图；其中和之间的系数表示相对时间为Δ时，节点对的重要性，可表示为：

利用归一化注意系数来计算每个节点的最终输出表示：

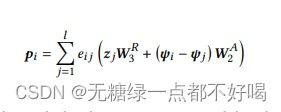
整个相对时态模块的输出可以表述为：

6.3 Decoder Module

采用双线性解码方案来计算当前用户的表示与每个候选项之间的相似度评分：

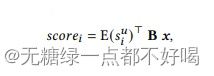
其中：B∈R×是一个可训练矩阵，E()是候选项的嵌入，然后将这些相似度得分取最大值，以获得每件商品被购买的概率。

6.4 Loss Function

文章的时间相关损失函数设计如下：

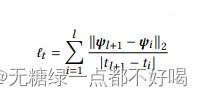
此外，利用似然的负对数形成二元交叉熵损失：

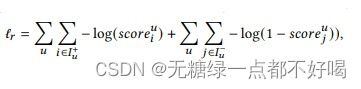
总损耗L由三项组成：预测损耗ℓ，自编码器损耗ℓ和时间损耗ℓ，线性组合如下：

7.实验

7.1 数据集

7.2 评价指标

1）F1-score：
采用每个用户平均，而不是全局平均，以达到更好的可解释性。

2）NDCG：
NDCG通过考虑正确项目的正确位置来评估排名性能，其可以被公式化如下：

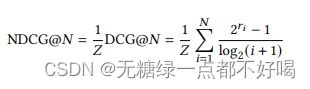
7.3 基线

POP、BPR、FPMC、GRU4Rec、narm、Time-LSTM、ATRank、TASER-Position、TASER-Abs

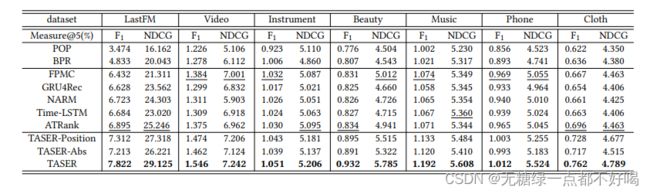
7.4 实验结果

1）通过模型相对于基线的实验结果和进行全面的消融研究，以此回应提出的研究问题；
2）模型可以有效地捕捉时间模式，从而在该数据集上获得更显著的收益。

8.结论

1）作者旨在利用用户行为序列中的绝对时间模式和相对时间模式进行顺序推荐；
2）文章提出了TASER，其中时间模式分别由绝对时间模块和相对时间模块捕获，并且在损失函数中采用时间感知约束以获得时间信息的更好表示；
3）在七个数据集上进行了广泛的实验，以验证TASER在建模时间模式方面的有效性；
4）实验结果表明，与现有技术相比，TASER能够显著获得更好的性能。

LaPlacian Eigenmaps

1.介绍

拉普拉斯特征映射（LaPlacian Eigenmaps）是一种基于图的降维算法，它从局部的角度去构建数据之间的关系。它希望在原空间中相互间有相似关系的点，在降维后的空间中尽可能的靠近，从而在降维后仍能保持原有的数据结构信息。

基本思想：拉普拉斯特征映射通过构建邻接矩阵为W的图，来重构数据流形的局部结构特征，目的是让相似的数据样例和在降维后的目标子空间里尽量接近。

2.步骤

1）构建图
使用某一种方法将所有的点构建成一个图；
2）确定权重
确定点与点之间的权重大小；
3）特征映射
计算拉普拉斯矩阵L的特征值与特征向量，选择m个最小的非零特征值对应的特征向量作为降维后的结果输出。

3.数学推导

通常采用高斯函数定义数据点之间的相似性，即

其中：σ是尺度参数，xi，xj对应两个数据样本。

最后，为了目标函数最小化，要选择m个最小的非零特征值所对应的特征向量，即可达到降维的目的。

问题：为什么选择m个最小的非零特征值对应的特征向量作为降维后的结果输出？
特征值越大对应的向量空间的方差越大，相应的分散程度也越大，即点与点之间越稀疏。拉普拉斯特征映射的目标是降维前有相似关系的样本在降维后也尽可能相似，所以选择方差小的向量空间，即选择最小特征值对应的向量空间。

4.算法实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from mpl_toolkits.mplot3d import Axes3D


# 1.生成swiss roll数据集
def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):
    t = 1.5 * np.pi * (1 + 2 * np.random.rand(1, n_samples))
    x = t * np.cos(t)
    y = 83 * np.random.rand(1, n_samples)
    z = t * np.sin(t)
    X = np.concatenate((x, y, z))
    X += noise * np.random.randn(3, n_samples)
    X = X.T
    t = np.squeeze(t)
    return X, t


# 2.用高斯函数定义数据点之间的相似性
def rbf(dist, t=1.0):
    return np.exp(-(dist / t))


# 3.计算两点间的距离
# (a - b)^2 = a^2 + b^2 - 2*a*b
def cal_pairwise_dist(x):
    sum_x = np.sum(np.square(x), 1)
    dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
    return dist


# 4.计算得到图的邻接矩阵
def cal_rbf_dist(data, n_neighbors=10, t=1):
    dist = cal_pairwise_dist(data)
    dist[dist < 0] = 0
    n = dist.shape[0]
    rbf_dist = rbf(dist, t)

    W = np.zeros((n, n))
    for i in range(n):
        index_ = np.argsort(dist[i])[1:1 + n_neighbors]
        W[i, index_] = rbf_dist[i, index_]
        W[index_, i] = rbf_dist[index_, i]

    return W


# 5.LE算法
def LE(data, n_dims=2, n_neighbors=5, t=1.0):
    N = data.shape[0]
    W = cal_rbf_dist(data, n_neighbors, t)
    D = np.zeros_like(W)
    for i in range(N):
        D[i, i] = np.sum(W[i])

    D_inv = np.linalg.inv(D)
    L = D - W
    eig_val, eig_vec = np.linalg.eig(np.dot(D_inv, L))

    sort_index_ = np.argsort(eig_val)

    eig_val = eig_val[sort_index_]
    print("eig_val[:10]: ", eig_val[:10])

    j = 0
    while eig_val[j] < 1e-6:
        j += 1

    print("j: ", j)

    sort_index_ = sort_index_[j:j + n_dims]
    eig_val_picked = eig_val[j:j + n_dims]
    print(eig_val_picked)
    eig_vec_picked = eig_vec[:, sort_index_]
    print(np.dot(np.dot(eig_vec_picked.T, D), eig_vec_picked))

    X_ndim = eig_vec_picked
    return X_ndim


if __name__ == '__main__':
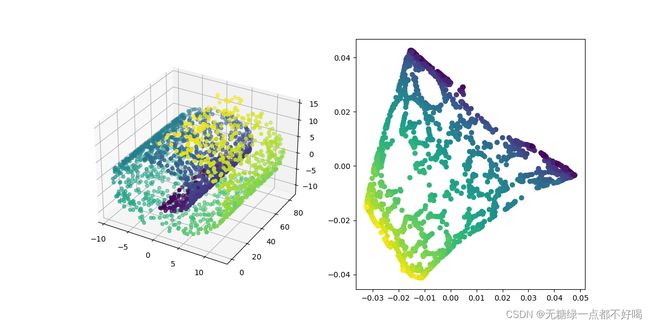
    X, Y = make_swiss_roll(n_samples=2000)
    X_ndim = LE(X, n_neighbors=5, t=20)

    fig = plt.figure(figsize=(12, 6))
    ax1 = fig.add_subplot(121, projection='3d')
    ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=Y)

    ax2 = fig.add_subplot(122)
    ax2.scatter(X_ndim[:, 0], X_ndim[:, 1], c=Y)
    plt.show()

降维后的效果图：

蚁群算法

在图论中，很多问题都是求某个规则下的最短路径，但因为规则不同，这些问题存在着本质上的不同，因此不能简单地都归于最短路径问题。其中：某些问题已经有有效算法，而有些问题至今没有有效算法。

1）Dijkstra算法：
它求解的是加权连通简单图中一个顶点到其它每个顶点具有最小权和的有向路，时间复杂度是O(n^2)，是多项式时间算法。
2）蚁群算法：
它是一种近似算法，它不是用来解决已存在精确有效算法的问题，而是用来解决至今没有找到精确有效算法的问题，比如旅行商问题（TSP）。
3）旅行商问题：
求一个完全图的最小哈密顿圈，这个问题至今未找到多项式时间算法。当问题规模稍大一点，现有的精确算法的运算量就会急剧增加。

上周学习了蚁群算法后，产生了一个疑问，就是寻找最短路径的时候，相较于Dijkstra算法，蚁群算法有哪些优势呢？蚁群算法开销比较大，而且还容易不收敛或者陷入局部最优。

区别：传统的最短路径算法（如Dijkstra算法等），存在局限是只能规划静态路径，而实际生活中所需要的路径规划往往是动态的。比如：在地震救援中有些路因为发生坍塌而无法行进，在实时交通路径规划中，有些地方因为堵车可被视为不能通行的路径，此时Dijkstra算法等传统的最短路径算法并不能适应路径的动态变化。对于这种尚未找到有效算法的问题，因此就产生了各种近似算法，以解的质量来换取效率，寻求满意解而不是最优解（蚁群算法）。

结论：蚁群算法是用来探索一个完全未知世界，并找到所求的解。

Navier-Stokes方程

1.流体微元（Fluid Element）和有限控制体（Control Volume）

在研究流体时，我们首先可以选取流体中的一个流体微元，且这个流体微元满足连续介质假设，即：
1）宏观上足够小，小到这个流体微元可以作为一个质点来看，与数学中的微分概念处于同一量级；
2）微观上足够大，大到其内部包含了足够多的流体分子，使分子尺度的无规则随机运动可以被忽略，从而表现出统一的物理特征，如压力、密度、温度等。

其次，还可以选取一个有限控制体来进行研究，这个控制体可以是空间中的任意形状，并且它的体积不再像流体微元那样局限在微观尺度，而是可以达到宏观量级，通过对这个控制体的积分特性进行研究从而得到流体控制方程。

因此：
1）以流体微元为研究对象将推导出微分型方程；
2）以有限控制体为研究对象将推导出积分型方程。

积分型方程与微分型方程的区别：
积分型方程允许在控制体内出现间断，而微分型方程由于涉及极限的概念，因此要求流场变量连续可导。因为散度定理要求变量连续可导，因此可以运用散度定理将积分型方程转化为微分型方程，其中积分型方程更适合于计算含有间断的流场。

2.欧拉法（Eulerian）和拉格朗日法（Lagrangian）

欧拉法，是以流体质点流经流场中各空间点的运动，即以流场作为描述对象研究流动的方法；拉格朗日法，跟随流体质点运动，记录该质点在运动过程中物理量随时间变化规律。
根据这两种方法推导得到的控制方程具有不同的形式，其中：
1）由欧拉法推导得到的是守恒型方程；
2）拉格朗日法推导得到的是非守恒型方程。

这两种方法与前面选取流体微元和控制体所推导出的不同形式方程进行组合，可以得到四种流体控制方程的表达形式：
1）积分守恒型方程：控制体+欧拉法；
2）积分非守恒型方程：控制体+拉格朗日法；
3）微分守恒型方程：流体微元+欧拉法；
4）微分非守恒型方程：流体微元+拉格朗日法。

---

总结

本周，我学习了新的降维算法，进一步讨论了蚁群算法和了解Navier-Stokes方程的基础知识；LaPlacian Eigenmaps算法，核心思想是通过计算数据点之间存在某种相似性来衡量局部结构，以此来实现降维效果；通过与多项式时间算法相比，得到了蚁群算法用于解决尚未找到有效算法的问题；上周用牛顿第二定律完成了对Navier-Stokes方程的数学推导，但Navier-Stokes方程中的基础知识还未了解，因此对Navier-Stokes方程的基础知识进行学习。下周，我将继续学习Navier-Stokes方程和新的降维方法，以及看一些微分几何和拓扑学的视频。