矩阵的实际意义
本文转载自十分钟理解线性代数的本质
我在上个月修了数值矩阵运算这门课 (Numerical Matrix Computing),对矩阵的变换和一些性质有了一定的理解。
在这里总结一下自己的研究的一些心得。
在经过了这次的学习之后,我由衷地感慨,我以前学的线性代数是什么鬼呀!
最近由于选修博士的课程《矩阵运算》。所以我重新在网上恶补了一遍《线性代数》的基本概念[1],对这门课有了全新的认识。
现在想想我大学学的线性代数,我真的会感慨,我之前都在学些什么呀!
如果你觉得自己当初线性代数也是学的一团雾水,不妨接着往下看看,绝对让你能够透彻的理解线性代数!
线性代数的本质
先一句话先把最重要的东西说了,什么是线性代数?
线性代数的本质,其实是一种高维空间上的变换。
这句话虽然简单,但这句话具体什么意思呢。别急,我们引入一个很直观的例子来理解这个数学表达。
拿二维空间中的小纸片人为例来说,小人在此:
我对一个小人进行位移,拉伸的一系列线性操作,它可以变成另一个样子:

这就是线性代数要做的一些事情。我对这个小人做的一些操作,就叫矩阵,也就是对这个对象的一些操作或者说映射。
所以乍一看,这个问题好像并没有什么特别难的,为啥线性代数这么难呢。
主要是很多的基本概念和实际的物理含义没有挂钩。
接下来,我们就来讲讲线性代数中的各个名词和物理含义的联系。
行列式
首先第一个概念就是矩阵的行列式。还记得刚开始学习线性代数的时候,老师上来就咔咔给我们一顿求解矩阵的行列式。
二阶矩阵的行列式是下面的这个公式,大家应该依稀还记得求矩阵的行列式的求法(不是定义),对角线相乘再相减:

然而,我还记得一个学期的线性代数学完了,我连第一个问题都没有解决。那就是,老师,咱们为什么要求一个矩阵的行列式?
为什么?
为什么?
在这里,我就来告诉大家,为什么要求解矩阵的行列式!
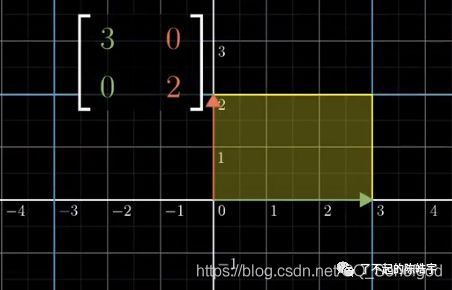
还是举一个例子,这次我们把上面的小纸片人换成一个面积是1*1的小方块:
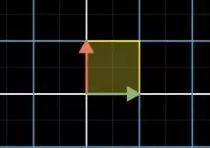
可以看到,经过了图中所示的矩阵的变换之后,我们之前的小方块变成了大一点的矩形,面积变成了3*2,也就是6。
而我们再算算图中这个矩阵的行列式的数值,也是6。
行列式的数值和矩阵变换之后的面积一样!
朋友们,这不是巧合!
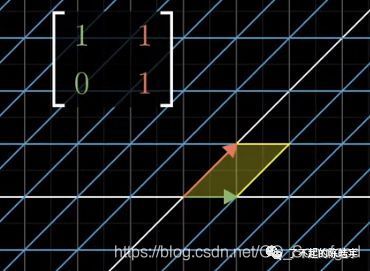
我们用另一个矩阵对原来的小方块进行一顿操作,可以看到之前的小方块变成了一个斜一点的矩形。
变换后的斜方形的面积是1,而图中这个矩阵变换的行列式的数值也是1。
行列式的数值和矩阵变换之后的面积仍然一样!
这!其实就是行列式的非常重要的物理意义!它其实就是矩阵变换带来的面积变化。
我第一次看到这个概念的时候,觉得醍醐灌顶,原来行列式的意义可以这么理解!
同时感慨,曾经我求解了不下一千个矩阵的行列式,原来自己根本不知道自己在求些什么东西!
当然,上面的定义是不准确的,对于二维来说,行列式代表的就是面积变化,三维来说,行列式表征的就是体积变化了,推之高维空间亦然。这样就严谨一些了。
逆矩阵
现在我们应该知道了矩阵是一种变换,想想上面的矩阵变换,我们可以把一个小方块变成一个斜斜的方块。
那么一定存在另一种矩阵的映射,能把这个斜斜的方块变回原来的小方块,是不是?
所以逆矩阵的物理意义就出来了,如果有个矩阵能把经过变换之后的斜斜的这个方块:

那么它就是原来那个矩阵的逆矩阵。
可以这么理解,逆矩阵就是一种对原矩阵的逆向变换。
对于逆矩阵,在数学上,有这么个表达:
A 是一个矩阵, A-1是A 的逆矩阵,它们相乘会得到一个单位矩阵。
结合物理意义我们就能理解这个公式了:一个物体经过了A矩阵的变换,在经过A 的逆矩阵的变换,就等于保持不变(单位矩阵就是保持不变)。
简单来说一句话,变过去又变回来,那就是没有变。
这就是逆矩阵的性质。
矩阵的秩
如果说上面的东西还只是有点意思的话,那接下来讲的东西就要进入高潮了。
由上面的论述,我们知道了逆矩阵是啥东西——就是一种反向变换。
一切看似没啥问题。
但是问题来了。我们喜欢折腾的数学家不久发现,有些矩阵变换没法求逆变换!
这是为什么呢?
这还要从矩阵的行列式说起。
我们从上面知道了,行列式表征的一种面积的变化。但是我们会发现有很多矩阵的行列式的数值是0。
啥意思呢?
很不严谨地举一个例子,想想我们上面提到的那个小方块。
现在有一种变换,让这个小方块的面积变换后变成零了。你觉得这是一个什么变换?
不知道你猜出来没(反正我一开始是没有头绪),只有一种可能:
以至于变换后的面积为零!
这就是行列式为零的物理意义。
借由这个物理意义,我们进一步可以知道:
如果一个矩阵变换的行列式为零,代表这个变换将对目标进行降维(比如从平面变成点)。
然后我们可以想象,一个物体维度一旦下降(比如从平面变成点),这个过程将不能逆转(从点重新恢复成平面)。
这就是为什么有些矩阵变换不能求逆矩阵!
进一步,我们就能得到线性代数里面最常用的一个结论:
行列式为0的矩阵是不可逆矩阵,不可逆矩阵的行列式就是0。
我第一次看到这个结论,内心是在咆哮的:
这就是传说中的降维打击啊!
科幻里面的东西原来就在身边,只是我一直没有去挖掘过!
那么什么又是矩阵的秩呢?
一句话解释就是,矩阵变换之后所给出的维度,就是矩阵的秩。
什么意思,打个比方,很简单,如果对一个三维物体进行一个矩阵变换,变成了一维的,那么这个矩阵的秩就是1,如果得到的是二维的,那么这个矩阵的秩就是2。
如果变换之后仍然是三维物体,那么这个矩阵的秩就是3,也叫做满秩(没有维度的损失)。
前两种情况下,经过矩阵变换后,维度都会下降,信息都会丢失。可以想象,他们相应的行列式都为零——对于一个三维物体,无论是变成了直线还是点,面积都是变成了0。
所以我们又得到了一个重要结论:
只有满秩的矩阵(变换之后维度不变)行列式才不为零。
我们可以看到,用物理含义来看这些定义,会显得格外通俗易懂。
特征根与特征向量
接下来我们来讲讲线性代数里面最最核心的最经典的一个问题:
求解矩阵的特征根和特征向量。
我刚开始学习矩阵这门课的时候,老师啥也没说,整节课就围绕着求解一个矩阵的特征向量和特征根展开了。
遗憾的是,我再次懵圈了,因为我连一个最基本的问题都没搞明白,嘿,老师,我们为啥要求解特征根和特征向量呀?
啥是矩阵的特征根?
啥事矩阵的特征向量?
啥?啥?啥?
于是我下课自己查看了相关资料之后,网友的一通介绍让我豁然开朗:
什么是特征向量呢,就是在高维空间中,经过了某个矩阵变换之后,保持不变的向量,就是这个矩阵的特征向量。
看不懂?
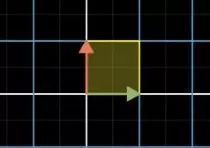
没关系,一如既往地,我们还是来举个例子。如下图,假设我们有一对向量是下面这个样子的:
经过了一个矩阵变换之后就变成了这个样子:
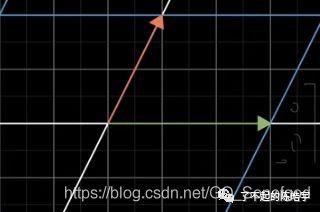
然后我们再随意的取另一个向量,黄色的箭头:
看看它经过了这个矩阵变换之后的样子:
可以看到,这个黄色的向量经过矩阵变换之后,方向和大小都改变了,注意那个粉色的延长线。
我们接下来再看一个经过了变换之后,方向可以不改变的向量,图中的黄色箭头:
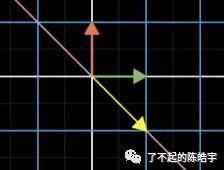
我们可以看到,经过了矩阵变换之后,这个黄色的箭头的方向保持了不变!
重点来了!!!
从物理意义来讲,这种经过了矩阵变换之后,方向依然能保持不变的向量,就是这个矩阵的特征向量,这些特征向量经过变换后大小的改变,就是该特征向量的对应特征值了。
为什么叫这个矩阵的特征向量呢,数学家说了,这是因为咱们只用这一个向量,就能代表这个矩阵的变换,所以叫做特征向量。
可能你又要问了,特征向量有啥用呢?
好的,例子再次登场!
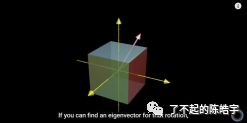
如下图,我们有一个立方体的物体:
我们现在对这个物体进行一波3D 旋转,得到下面这个样子:
虽然我告诉旋转的过程是,红的那一面从右边转到了左边。
但是你可能还是很难想象它到底是怎么转过来的,对吧?
计算机也很难想到!
然后,怎么办呢?
为了直观起见,我们可以想象一下这给它添加一个旋转轴,如下图:
它旋转的时候,就是围绕着这个轴来转的:
你可能会说,行吧,好像能想象出来了。
但是旋转就旋转吧,和特征向量有啥关系呢。
人数学家说了,这个旋转其实就是一种矩阵变换,而这个轴就叫做这个旋转变换的特征向量!
因为在整个变换中,只有这个轴的方向是没有改变的!
也就是说,我们找到了这个轴,也就是特征向量,我们就找到了这个旋转,也就是矩阵变换的最简洁的表征方法!
基于上述的这个理论,在现代的矩阵求解特征向量的运算中,有一个叫 Power 迭代法 的算法被广泛用于计算机求解矩阵的特征向量。
它的原理就是基于——特征向量就是,经过矩阵变换后,方向保持不变的向量。
Power 迭代法 它具体是怎么进行求解一个矩阵的特征向量的呢?非常简单。
我们首先任意选一个向量,对它进行矩阵的变换,然后得到一个新的向量,我们再对这个新的向量进行矩阵变换,如此反复。我们可以想见,经过了无数次的矩阵变换后,向量会趋近于不变。而这就是特征向量的定义——经过矩阵变换后,方向保持不变的向量。
以上,就是我在课余时间对线性代数物理含义的一些总结。
总结
通过线性代数的学习,我的收获很大。一方面,我发现学习一定要多问为什么,把整个事情的来龙去脉摸清楚。如果只是一知半解,那么不仅学的知识很不牢固,学习的时候也会很枯燥。
另一方面,借用万门大学(一个网上课堂)的老师的一句话来说就是:
所以我们学的越多,我们发现自己不懂的东西越多,但是我们的知识体系变大,仍然是一件有趣的事情,因为它可以更好的帮助我们做决策。
以及如果我们不去扩大自己的知识体系,生命实在是太无聊了,翻来覆去就那几种需求。
多多学习新的知识,探索别人没有发现过的乐趣,真的能让人感受快乐。