力扣LeetCode刷题笔记总结1

题型一：数组

0.数组的基础知识

（1）数组下标都是从0开始的，数组内存空间的地址是连续的。因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

（2）数组的元素是不能删的，只能覆盖。

（3）C++中，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

1.二分查找

解法1：左闭右闭的区间

定义target在[left, right]区间内，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

class Solution {
public:
    int search(vector& nums, int target) {
      int left=0,right=nums.size()-1;
      while(left<=right){        //此处循环不能少  while(left<=right)
          int mid=(right-left)/2+left;       //错误代码 int mid=(right+left)/2+left;
          if(nums[mid]==target){
             return mid;
          }else if (nums[mid]

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度

• 空间复杂度：O(1)

 解法2：左闭右开的区间

定义 target 在[left, right)区间中 ，那么有如下两点：

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

class Solution {
public:
    int search(vector& nums, int target) {
      int left=0,right=nums.size();
      while(left

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度

• 空间复杂度：O(1)

2.搜索插入位置

 解法1：二分查找(左闭右闭)

题眼：有序+无重复

class Solution {
public:
    int searchInsert(vector& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<=right){
            int mid=(right-left)/2+left;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
        return left;
    }
};

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度

• 空间复杂度：O(1)

 解法2：二分查找(左闭右开) 

class Solution {
public:
    int searchInsert(vector& nums, int target) {
        int left=0,right=nums.size();  //不同点1
        while(lefttarget){
                right=mid;   //不同点3
            }else {
                left=mid+1;
            }
        }
        return left;
    }
};

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度

• 空间复杂度：O(1)

 3.*在排序数组中查找元素的第一个和最后一个位置

解法1：二分查找（左闭右闭）

 思路：考虑 target 开始和结束位置，我们要找的就是数组中「第一个等于 target 的位置」（记为leftIdx）和「第一个大于 target的位置减一」（记为 rightIdx）。

class Solution {
public:
    int binarysearch(vector& nums,int target,bool lower){
       int left=0,right=nums.size()-1;
       int ans=nums.size();     // ans初始化不能是0
       while(left<=right){
           int mid=(right-left)/2+left;
           // 如果 lower 为 true，则查找第一个大于等于 target 的下标，（找到左下标）
           // 否则查找第一个大于 target 的下标。（找到右下标）
           if(nums[mid] > target || (lower&&nums[mid] >= target)){
               right=mid-1;
               ans=mid;
           }else{
               left=mid+1;
           }
       }
       return ans;
    }

    vector searchRange(vector& nums, int target) {
         int leftIdx=binarysearch(nums,target,true);
         int rightIdx=binarysearch(nums,target,false)-1;
         if(leftIdx<=rightIdx&&rightIdx<=nums.size()-1&&nums[leftIdx]==target&&nums[rightIdx]==target){
             return vector{leftIdx,rightIdx};
         }
         return vector{-1,-1};
    }
};

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度

• 空间复杂度：O(1)

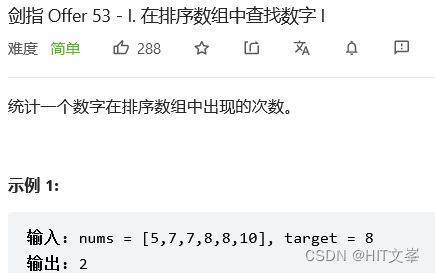
4.#在排序数组中查找数字

 解法1：二分查找

class Solution {
public:
    int binarysearch(vector& nums,int target,bool lower){
       int left=0,right=nums.size()-1,ans=nums.size();
       while(left<=right){
           int mid=(right-left)/2+left; //求 mid 在 while 内
           // 如果 lower 为 true，则查找第一个大于等于 target 的下标，（找到左下标）
           // 否则查找第一个大于 target 的下标。（找到右下标）
           if(nums[mid] > target || (lower&&nums[mid] >= target)){
               right=mid-1;
               ans=mid;
           }else{
               left=mid+1;
           }
       }
       return ans;
    }

    int search(vector& nums, int target) {
         int leftIdx=binarysearch(nums,target,true);
         int rightIdx=binarysearch(nums,target,false)-1;
         if(leftIdx<=rightIdx&&rightIdx<=nums.size()-1&&nums[leftIdx]==target&&nums[rightIdx]==target){
             return rightIdx-leftIdx+1;
         }
         return 0;
    }
};

• 时间复杂度：O(log⁡n)，其中 n 是数组的长度。二分查找的时间复杂度为 O(log⁡n)，一共会执行两次，因此总时间复杂度为 O(log⁡n)。

• 空间复杂度：O(1)。只需要常数空间存放若干变量。

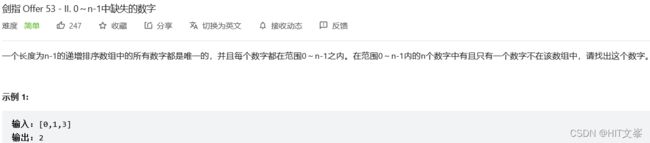
5. #0~n-1中缺失的数字

 解法1：二分查找

class Solution {
public:
    int missingNumber(vector& nums) {
        int left=0,right=nums.size()-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==mid){
                left=mid+1;
            }else{
                right=mid-1;
            }
        }
        return left;
    }
};

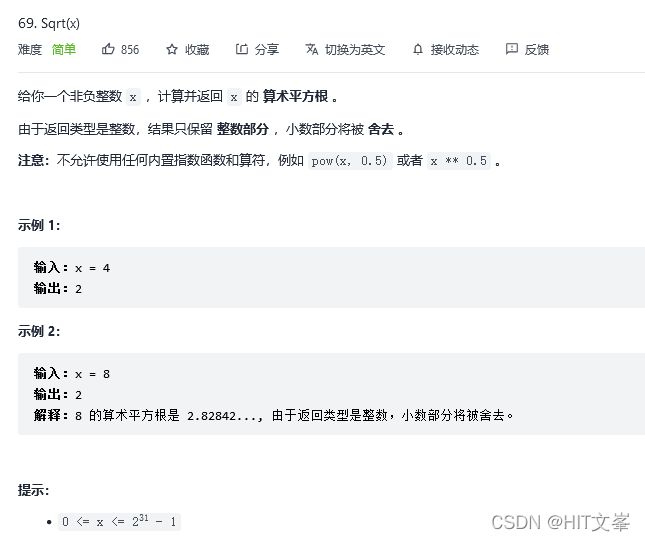
6. Sqrt(x)

 

 解法1：二分查找（左闭右闭）

class Solution {
public:
    int mySqrt(int x) {
        int left=0,right=x,ans=-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if((long long)mid*mid<=x){
                left=mid+1;     // 因为要舍弃小数，所以一定要先考虑左边界
                ans=mid;     
            }else{
                right=mid-1;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(log⁡x)，即为二分查找需要的次数。

• 空间复杂度：O(1)

解法2：数学转换

class Solution {
public:
    int mySqrt(int x) {
      if(x==0){
          return 0;
      }
      int ans=exp(0.5*log(x));
      //计算机无法存储浮点数的精确值，而对数函数和指数函数的参数和返回值均为浮点数
      return ((long long)(ans+1)*(ans+1)<=x?(ans+1):ans); 
    }
};

• 时间复杂度：O(1)，由于内置的 exp 函数与 log 函数一般都很快，这里将其复杂度视为 O(1)

• 空间复杂度：O(1)

7.有效的完全平方数

 解法1：二分查找（左闭右闭）

class Solution {
public:
    bool isPerfectSquare(int num) {
        int left=0,right=num;
        while(left<=right){
            int mid =(right-left)/2+left;
            if((long long)mid*mid==num){
                return true;
            }else if((long long)mid*mid

• 时间复杂度：O(log ⁡n)，其中 n 为正整数 num 的最大值

• 空间复杂度：O(1)

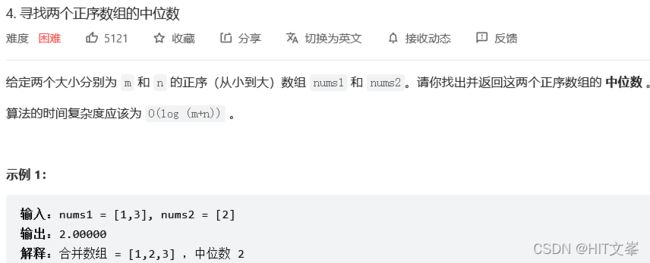
8.*寻找两个正序数组的中位数

 解法1：二分查找

思路： nums1 和 nums2 的相对位置并不会发⽣变化，在排好序的数组中查找，很容易想到可以⽤二分查找（Binary Search)，对小的数组进⾏二分可降低时间复杂度

class Solution { 
public:
    double findMedianSortedArrays(vector& nums1, vector& nums2) {
        if(nums1.size()>nums2.size()) swap(nums1,nums2);
        //return findMedianSortedArrays(nums2,nums1);
        int m=nums1.size(),n=nums2.size();
        int left=0,right=m;    // m个数有m+1种分割方法，所以不取right=m-1
        int maxLeft=0,minRight=0;
        while(left<=right){ 
            //i,j 分别为两个数组的分割点：nums1[i-1],nums1[i],nums2[j-1],nums2[j]
            int i=left+(right-left)/2;
            int j=(m+n+1)/2-i;    //因为有关系：i+j=(m+n+1)/2
            int left1  = (i==0?INT_MIN:nums1[i-1]);
            int right1 = (i==m?INT_MAX:nums1[i]);
            int left2  = (j==0?INT_MIN:nums2[j-1]);
            int right2 = (j==n?INT_MAX:nums2[j]);
            if(left1 <= right2){
                maxLeft=max(left1 , left2);
                minRight=min(right1 , right2);
                left=i+1;
            }else {
                right=i-1;
            }
        }
        return (m+n)%2 ? maxLeft : (maxLeft+minRight)/2.0;
    }
};

• 时间复杂度：O(log⁡min⁡(m,n))，其中 m 和 n 分别是数组 nums1 和 nums2​ 的长度。

• 空间复杂度：O(1)

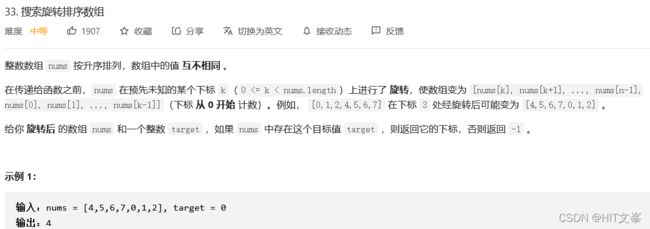
9.*搜索旋转排序数组

解法1：二分查找

 思路：题眼：升序+时间复杂度为O(log n)  => 二分查找

class Solution {       
public:
    int search(vector& nums, int target) {
        int n=nums.size();
        int left=0,right=n-1;
        // if(!n) return -1;
        // if(n==1) return nums[0]==target ?0:-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==target) return mid;
            //关键判断那一部分有序
            if(nums[mid]>=nums[0]){   //mid 在左边有序部分
                if(nums[0]<=target && target

• 时间复杂度：O(log⁡n)，其中 n 为 nums 数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(log⁡n)。

• 空间复杂度：O(1)。我们只需要常数级别的空间存放变量。

10.寻找旋转排序数组中的最小值

 

 解法1：二分查找

class Solution {
public:
    int findMin(vector& nums) {
        int left=0,right=nums.size()-1;  // 左闭右闭区间，如果用右开区间则不方便判断右值
        while(leftnums[right]){
                left=mid+1;
            }
        }
        return nums[left];
    }
};

• 时间复杂度：O(log⁡n)，其中 n 为 nums 数组的大小。在二分查找的过程中，每一步会忽略一半的区间，因此时间复杂度为 O(log⁡n)。

• 空间复杂度：O(1)。我们只需要常数级别的空间存放变量。

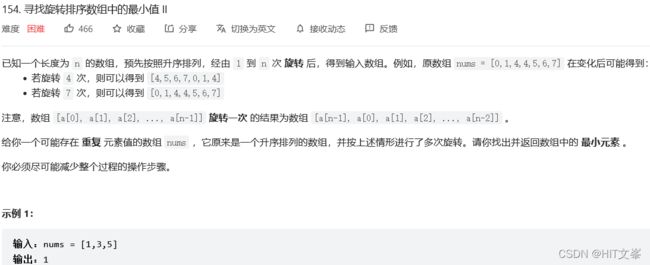
11.寻找旋转排序数组中的最小值II  

 解法1：二分查找（含重复项）

思路：特别地，nums[mid]==nums[right]。由于重复元素的存在，我们并不能确定 nums[mid] 究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论 nums[high] 是不是最小值，都有一个它的「替代品」nums[mid]，因此我们可以忽略二分查找区间的右端点。

class Solution {
public:
    int findMin(vector& nums) {
        int left=0,right=nums.size()-1;
        while(leftnums[right]){
                left=mid+1;
            }else{
                right-=1;   // 处理重复项
            }
        }
        return nums[left];
    }
};

• 时间复杂度：平均时间复杂度为 O(log⁡n)，其中 n 是数组 nums 的长度。如果数组是随机生成的，那么数组中包含相同元素的概率很低，在二分查找的过程中，大部分情况都会忽略一半的区间。而在最坏情况下，如果数组中的元素完全相同，那么 while 循环就需要执行 n 次，每次忽略区间的右端点，时间复杂度为 O(n)。

• 空间复杂度：O(1)。我们只需要常数级别的空间存放变量。

12.#旋转数组的最小数字

 解法1：二分查找（含重复项）

class Solution {  
public:
    int minArray(vector& numbers) {
        int left=0,right=numbers.size()-1;
        while(leftnumbers[right]){
                left=mid+1;
            }else{
                right-=1;
            }
        }
        return numbers[left];
    }
};

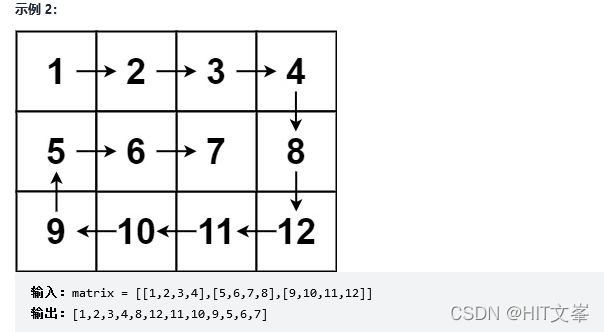
13.搜索二维矩阵

解法1：暴力

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        for(const auto&row:matrix){
            for(int element:row){
                if(element==target){
                    return true;
                }
            }
        }
        return false;   
    }
};

• 时间复杂度：O(m⁡n)。

• 空间复杂度：O(1)。

解法2：二分查找

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        for(const auto&row:matrix){
            //每一行都使用一次二分查找
            //lower_bound()返回值是一个迭代器,返回指向大于等于key的第一个值的位置
            //upper_bound()函数，它返回大于key的第一个元素
            auto it=lower_bound(row.begin(),row.end(),target);
            if(it!=row.end() && *it==target){
                return true;
            }
        }
        return false;
    }
};

• 时间复杂度：O(mlog⁡n)。对一行使用二分查找的时间复杂度为 O(log⁡n)，最多需要进行 m 次二分查找。

• 空间复杂度：O(1)。

解法3：Z字形查找

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }else if (matrix[x][y] > target) {
                --y;
            }else {
                ++x;
            }
        }
        return false;
    }
};

• 时间复杂度：O(m+n)。在搜索的过程中，如果我们没有找到 target，那么我们要么将 y 减少 1，要么将 x 增加 1。由于 (x,y) 的初始值分别为 (0,n−1)，因此 y 最多能被减少 n 次，x 最多能被增加 m 次，总搜索次数为 m+n。在这之后，x 和 y 就会超出矩阵的边界。

• 空间复杂度：O(1)。

解法4：二分查找（二维降一维）

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int left = 0, right = m*n - 1;
        while (left<=right) {
            int mid=left+(right-left)/2;
            if (matrix[mid/n][mid%n] == target) {
                return true;
            }else if (matrix[mid/n][mid%n] > target) {
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
        return false;
    }
};

• 时间复杂度：O(logmn)，其中 m 和 n 分别是矩阵的行数和列数。

• 空间复杂度：O(1)。

14.*搜索二维矩阵II

解法1：暴力

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        for(const auto&row:matrix){
            for(int element:row){
                if(element==target){
                    return true;
                }
            }
        }
        return false;   
    }
};

• 时间复杂度：O(m⁡n)。

• 空间复杂度：O(1)。

解法2：二分查找

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        for(const auto&row:matrix){
            //每一行都使用一次二分查找
            //lower_bound()返回值是一个迭代器,返回指向大于等于key的第一个值的位置
            //upper_bound()函数，它返回大于key的第一个元素
            auto it=lower_bound(row.begin(),row.end(),target);
            if(it!=row.end() && *it==target){
                return true;
            }
        }
        return false;
    }
};

• 时间复杂度：O(mlog⁡n)。对一行使用二分查找的时间复杂度为 O(log⁡n)，最多需要进行 m 次二分查找。

• 空间复杂度：O(1)。

解法3：Z字形查找

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }else if (matrix[x][y] > target) {
                --y;
            }else {
                ++x;
            }
        }
        return false;
    }
};

• 时间复杂度：O(m+n)。在搜索的过程中，如果我们没有找到 target，那么我们要么将 y 减少 1，要么将 x 增加 1。由于 (x,y) 的初始值分别为 (0,n−1)，因此 y 最多能被减少 n 次，x 最多能被增加 m 次，总搜索次数为 m+n。在这之后，x 和 y 就会超出矩阵的边界。

• 空间复杂度：O(1)。

15.#二维数组中的查找

 

解法1：暴力

class Solution {
public:
    bool findNumberIn2DArray(vector>& matrix, int target) {
        for(const auto&row:matrix){
            for(int element:row){
                if(element==target){
                    return true;
                }
            }
        }
        return false; 
    }
};

解法2：二分查找

class Solution {
public:
    bool findNumberIn2DArray(vector>& matrix, int target) {
        for(const auto&row:matrix){
            //每一行都使用一次二分查找
            //lower_bound()返回值是一个迭代器,返回指向大于等于key的第一个值的位置
            //upper_bound()函数，它返回大于key的第一个元素
            auto it=lower_bound(row.begin(),row.end(),target);
            if(it!=row.end() && *it==target){
                return true;
            }
        }
        return false;
    }
};

 解法3：Z字形查找

class Solution {
public:
    bool findNumberIn2DArray(vector>& matrix, int target) {
        int m = matrix.size();
        if(m==0) return false;     // 防止空数组
        int n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }else if (matrix[x][y] > target) {
                --y;
            }else {
                ++x;
            }
        }
        return false;
    }
};

class Solution {
public:
    bool findNumberIn2DArray(vector>& matrix, int target) {
        int m = matrix.size();
        int x = m-1, y = 0;
        while (x >= 0 && y < matrix[0].size()) {
            if (matrix[x][y] == target) {
                return true;
            }else if (matrix[x][y] > target) {
                --x;
            }else {
                ++y;
            }
        }
        return false;
    }
};

16.移除元素

  解法1：快慢指针

class Solution {
public:
    int removeElement(vector& nums, int val) {
        int left=0;
        for(int right=0;right

• 时间复杂度：O(⁡n)，其中 n 为序列的长度。我们只需要遍历该序列至多两次

• 空间复杂度：O(1)，只需要常数的空间保存若干变量

解法2：前后指针

class Solution {
public:
    int removeElement(vector& nums, int val) {
        int left=0,right=nums.size()-1;
        while(left<=right){
           if(nums[left]==val){
               nums[left]=nums[right];
               right--;
           }else{
               left++;
           }
        }
        return left;
    }
};

• 时间复杂度：O(⁡n)，其中 n 为序列的长度。我们只需要遍历该序列至多一次

• 空间复杂度：O(1)，只需要常数的空间保存若干变量

17.删除有序数组中的重复项

 解法1：快慢指针

class Solution {
public:
    int removeDuplicates(vector& nums) {
      if (nums.size()==0){
          return 0;
      }     
      int slow=1,fast=1;   //slow也必须是从1开始
      while(fast

• 时间复杂度：O(⁡n)，其中 n 是数组的长度。快指针和慢指针最多各移动 n 次

• 空间复杂度：O(1)，只需要常数的空间保存若干变量

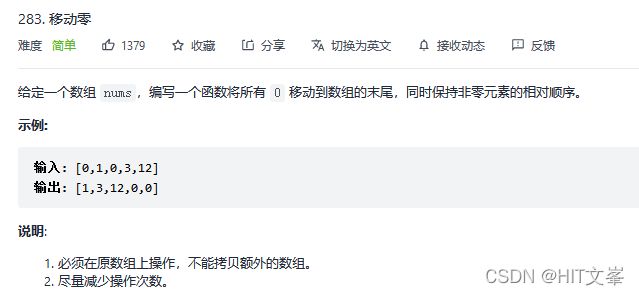
 18.移动零

解法1：快慢指针（while循环）

class Solution {
public:
    void moveZeroes(vector& nums) {
       int left=0,right=0;
       while(right

• 时间复杂度：O(⁡n)，其中 n 为序列长度。每个位置至多被遍历两次

• 空间复杂度：O(1)，只需要常数的空间保存若干变量

解法2：快慢指针（for循环）

class Solution {
public:
    void moveZeroes(vector& nums) {
       int left=0,right=0;
       for(right;right

• 时间复杂度：O(⁡n)

• 空间复杂度：O(1)

19.比较含退格的字符串

 

 解法1：双指针（逆序遍历）

class Solution {
public:
    bool backspaceCompare(string s, string t) {
       int i=s.length()-1,j=t.length()-1;
       int skips=0,skipt=0;  //skip 表示当前待删除的字符的数量
       while(i>=0||j>=0){
            while(i>=0){      //逆序遍历字符串，因为字符后的#决定该字符是否会被删除
                if(s[i]=='#'){
                    skips++;
                    i--;
                }else if(skips>0){
                    skips--;
                    i--;
                }else{
                    break;  //while 结束循环
                }
            }
            while(j>=0){  
                if(t[j]=='#'){
                    skipt++;
                    j--;
                }else if(skipt>0){
                    skipt--;
                    j--;
                }else{
                    break;
                }
            }
            
            /* else 的3种情况
               1. i < 0 && j >= 0
               2. j < 0 && i >= 0
               3. i < 0 && j < 0
               其中，第 3 种情况为符合题意情况，因为这种情况下 s 和 t 都是 index = 0 的位置为 '#' ，则 i, j 会为 -1，
               而这种情况下退格空字符即为空字符，也符合题意，应当返回 True。  */
            if(i>=0 && j>=0){
               if(s[i]!=t[j])  return false;
            }else if(i>=0||j>=0){
               return false;
            }
        i--,j--;           
       }
      return true;
    }
};

• 时间复杂度：O(⁡n+m)，其中 n 和 m 分别为字符串 s 和 t 的长度。我们需要遍历两字符串各一次

• 空间复杂度：O(1)，对于每个字符串，我们只需要定义一个指针和一个计数器即可

 解法2：栈

思路：用栈处理遍历，每次我们遍历到一个字符： 如果它是退格符，那么我们将栈顶弹出；如果它是普通字符，那么我们将其压入栈中。

class Solution {
public:
    string bluid(string str){
        string ans;
        for(char ch:str){
            if(ch!='#'){
                ans.push_back(ch);
            }else if(!ans.empty()){
                ans.pop_back();
            }
        }
        return ans;
    }
    bool backspaceCompare(string s, string t) {   
        return bluid(s)==bluid(t);
    }
};

• 时间复杂度：O(⁡n+m)，其中 n 和 m 分别为字符串 s 和 t 的长度。我们需要遍历两字符串各一次

• 空间复杂度：O(n+m)，其中 n 和 m 分别为字符串 s 和 t 的长度。主要为还原出的字符串的开销

20.有序数组的平方

 解法1：前后指针

思路：利用有序的特点，直接比较前后的两个数的最大者

class Solution {
public:
    vector sortedSquares(vector& nums) {
       vector ans(nums.size());        //ans(nums.size())注意容器大小的设置
       for(int i=0,j=nums.size()-1,pos=nums.size()-1;i<=j;){// 注意这里要i <= j，因为最后要处理两个元素
           //选择较大的那个数，逆序放入答案并移动指针
           if(nums[i]*nums[i]

• 时间复杂度：O(⁡n)，其中 n 是数组 nums 的长度

• 空间复杂度：O(1)，除了存储答案的数组以外，我们只需要维护常量空间

解法2：双指针+归并排序

class Solution {
public:
    vector sortedSquares(vector& nums) {
        int n = nums.size();
        int negative = -1;   //找出正数和负数的分界点
        for (int i = 0; i < n; ++i) {
            if (nums[i] < 0) {
                negative = i;
            } else {
                break;
            }
        }

        vector ans;
        int i = negative, j = negative + 1;
        while (i >= 0 || j < n) {
            //当某一指针移至边界时，将另一指针还未遍历到的数依次放入答案
            if (i < 0) {
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }else if (j == n) {
                ans.push_back(nums[i] * nums[i]);
                --i;
            }
            //每次比较两个指针对应的数，选择较小的那个放入答案并移动指针
            else if (nums[i] * nums[i] < nums[j] * nums[j]) {
                ans.push_back(nums[i] * nums[i]);
                --i;
            }else {
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(⁡n)，其中 n 是数组 nums 的长度

• 空间复杂度：O(1)，除了存储答案的数组以外，我们只需要维护常量空间

 解法3：利用内置函数sort直接排序

class Solution {
public:
    vector sortedSquares(vector& nums) {
       vector ans;
       for(int num:nums){
          ans.push_back(num*num);
       }
       sort(ans.begin(),ans.end());
       return ans;
    }
};

• 时间复杂度：O(nlogn)，其中 n 是数组 nums 的长度

• 空间复杂度：O(logn)。除了存储答案的数组以外，我们需要 O(log⁡n) 的栈空间进行排序

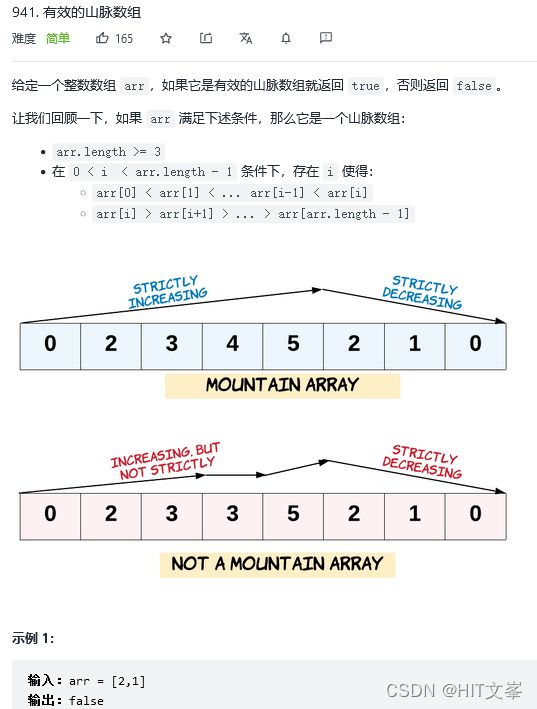
21.有效的山脉数组

 解法1：前后指针

class Solution {    //双指针：左到中间递增，右到中间递增
public:
    bool validMountainArray(vector& arr) {
        if(arr.size()<3) return false;
        int left=0,right=arr.size()-1;
        //注意 left 和 right 不能超过数组的边界
        while(left0 && arr[right-1]>arr[right]) --right;
        //最终判断两个指针是否在中间相遇，并且相遇点不能是左边界也不能是又边界！！
        return left==right && left!=0 && right!=arr.size()-1;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 arr 的长度

• 空间复杂度：O(1)

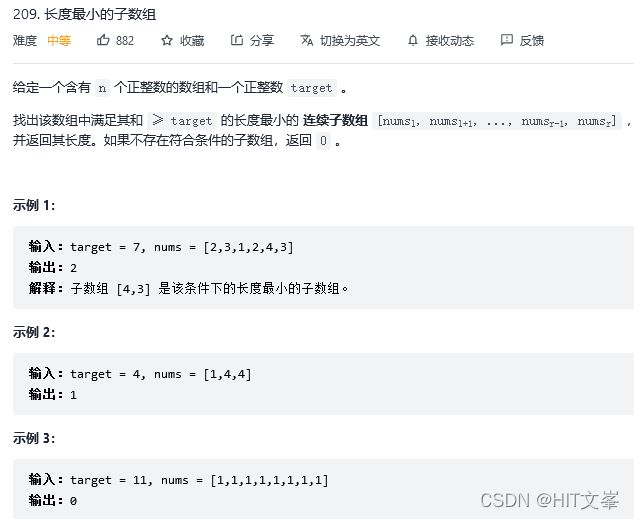
22. 长度最小的子数组

解法1：滑动窗口

滑动窗口：不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

class Solution {
public:
    //每次确定子数组的开始下标，然后得到长度最小的子数组，时间复杂度高
    int minSubArrayLen(int target, vector& nums) {
        int start=0,end=0,n=nums.size();
        int sum=0,ans=INT_MAX;
        if(n==0) return 0;     //0个元素的特殊情况需要考虑
        for(;end=target){
                ans=min(ans,end-start+1);
                sum-=nums[start];
                start++;
            }
            
        }
        return ans==INT_MAX?0:ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次

• 空间复杂度：O(1)

并不是while中放while就认为时间复杂度是 O(n^2)，主要是看每一个元素被操作的次数，每个元素在滑动窗口中进来操作一次，出去操作一次，每个元素都是被被操作两次，所以时间复杂度是 2 × n ，也就是 O(n)

23.水果成篮

解法1：滑动窗口+哈希

问题等价于：找到最长的包含两种不同“类型”的子序列 

class Solution {
public:
    int totalFruit(vector& fruits) {
        unordered_map basket;   //哈希表保证篮子里的水果种类不超过2
        int ans=INT_MIN,start=0;
        for(int end=0;end=3){  //直到种类超过2，才会滑动窗口
                basket[fruits[start]]--;
                if(basket[fruits[start]]==0){//直到把多出的那种水果全部移除
                    basket.erase(fruits[start]);                    
                }
                start++;
            }
            ans=max(ans,end-start+1);
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是 fruits 的长度

• 空间复杂度：O(n)

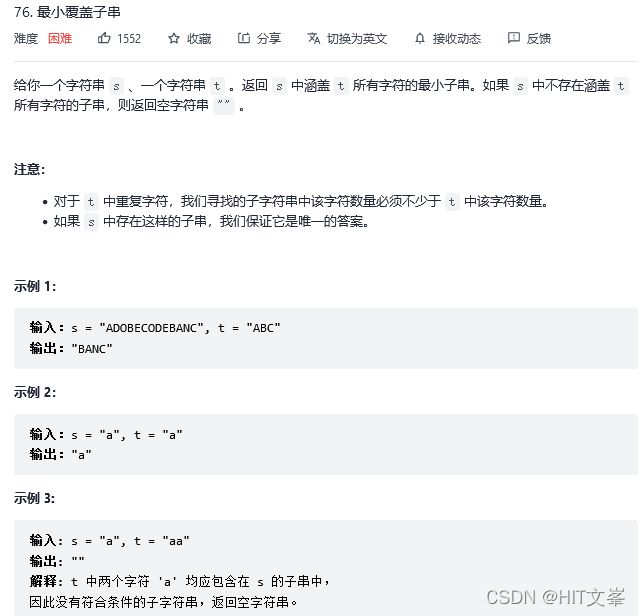
24.*最小覆盖字串

 

 

 解法1：滑动窗口+哈希

思路：用一个哈希表记录 t 中所有的字符以及它们的个数，用另一个哈希表动态维护窗口中所有的字符以及它们的个数。如果这个动态表中包含 t 的哈希表中的所有字符，并且对应的个数都不小于 t 的哈希表中各个字符的个数，那么当前的窗口是「可行」的

class Solution {
private:
    //判断窗口中是否全包含t中所有的字符
    bool check(){
        for(const auto &p:t_map){
            if(window_map[p.first] < p.second){
                return false;
            }
        }
        return true;
    }
    unordered_map window_map,t_map;
public:
    string minWindow(string s, string t) {
        for(const auto &c:t){
            ++t_map[c];
        }
        //ansL 存储窗口的左指针索引，len 窗口的长度
        int left=0,ansL=-1,len=INT_MAX;
        for(int right=0;right < s.length();++right){ //直到右指针移动到字符串的末尾
            //步骤1、往滑动窗口中添加字符（移动右指针）
            //s 中的右指针移动后的字符存在于 t 中（即在s中查找t中是否存在该元素），则增加到滑动窗口中
            if(t_map.find(s[right]) != t_map.end()){
                ++window_map[s[right]];
            }
            //步骤2、开始移动滑动窗口（移动左指针）
            while(check() && left<=right){
                if(t_map.find(s[left]) != t_map.end()){
                    --window_map[s[left]];
                }
                //更新滑动窗口的长度 和 滑动窗口的左指针
                if(right-left+1 < len){
                    len=right-left+1;
                    ansL=left;
                }
                ++left;
            }
        }
        return ansL==-1 ? "" :s.substr(ansL,len);
    }
};

• 时间复杂度：O(C⋅∣s∣+∣t∣)，其中 C 是字符集大小。最坏情况下左右指针对 s 的每个元素各遍历一遍，哈希表中对 s 中的每个元素各插入、删除一次，对 t 中的元素各插入一次。

• 空间复杂度：O(C)，其中 C 是字符集大小。两张哈希表作为辅助空间，每张哈希表最多不会存放超过字符集大小的键值对。

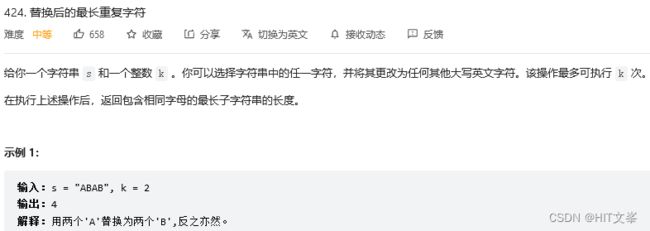
25.替换后的最长重复字串

解法1：滑动窗口

class Solution {
public:
    int characterReplacement(string s, int k) {
        int left=0, right=0;
        int mx=0;
        vector nums(26);    // 字符串中仅包含大写字母
        for(; right mx+k){
                nums[s[left]-'A']--;         // 左窗口移动，移出滑动窗口时，要将响应的值删除
                left++;
            }
        }
        return right-left;
    }
};

26.存在重复元素

解法1： 哈希

class Solution {
public:
    bool containsDuplicate(vector& nums) {
       unordered_set s;
       for(int x:nums){
           if(s.find(x)!=s.end()){
               return true;
           }
           s.insert(x);
       }
       return false;
    }
};

 27.存在重复元素II

 解法1：滑动窗口+哈希

思路：如果一个滑动窗口的结束下标是 i，则该滑动窗口的开始下标是 max⁡(0,i−k)。可以使用哈希集合存储滑动窗口中的元素。

class Solution {
public:
    bool containsNearbyDuplicate(vector& nums, int k) {
        unordered_set uset;
        for(int i=0; i0) uset.erase(nums[i-k-1]);

            if(uset.count(nums[i])) return true;
            uset.emplace(nums[i]);
        }
        return false;
    }
};

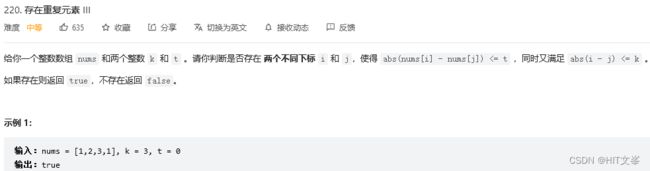
28.存在重复元素III

 解法1：滑动窗口+有序集合

class Solution {
public:
    bool containsNearbyAlmostDuplicate(vector& nums, int k, int t) {
        set s;
        for (int i = 0; i < nums.size(); i++) {
            auto iter = s.lower_bound(max(nums[i], INT_MIN + t) - t);
            if (iter != s.end() && *iter <= min(nums[i], INT_MAX - t) + t) {
                return true;
            }
            s.insert(nums[i]);
            if (i >= k) {
                s.erase(nums[i - k]);
            }
        }
        return false;
    }
};

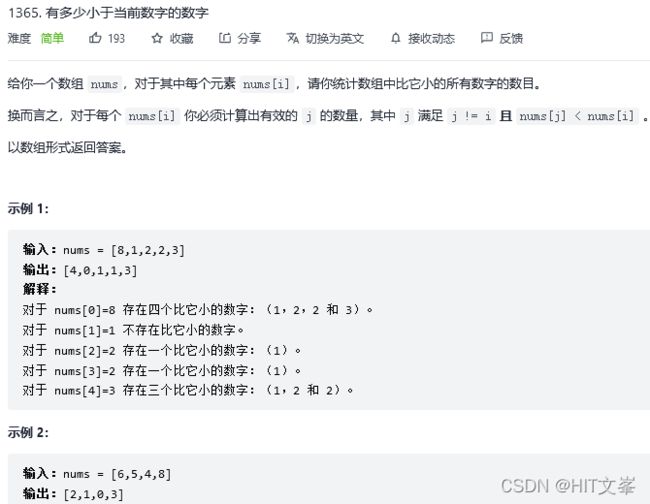
29.有多少小于当前数字的数字

 解法1：排序+哈希

class Solution {
public:
    vector smallerNumbersThanCurrent(vector& nums) {
        vector vec=nums;
        sort(vec.begin(),vec.end()); //排序，元素下标就是小于当前元素的数字
        int hash[101];  //哈希：数值和下标的映射
        // 有数字相同时，从后向前遍历，可以知道hash里存放的就是 相同元素最左面 的数值和下标
        for(int i=vec.size()-1;i>=0;--i){
            hash[vec[i]]=i;          //记录 vec[i] 对应的下标
        }
        // 此时hash里保存的每一个元素数值 对应的 小于这个数值的个数
        for(int i=0;i

• 时间复杂度：O(nlogn)

• 空间复杂度：O(n)

30.轮转数组

 解法1：数组翻转

思路：右旋转的顺序：1、整体反转字符串  2、反转区间为前 k 的子串 3、反转区间为 k 到末尾的子串。左旋转的顺序：1、反转区间为前 k 的子串 2、反转区间为 k 到末尾的子串 3、整体反转字符串

class Solution {
public:
    void rotate(vector& nums, int k) {
        k=k%nums.size();   //考虑到 k大于nums.size()
        reverse(nums.begin(),nums.end());
        reverse(nums.begin(),nums.begin()+k);
        reverse(nums.begin()+k,nums.end()); 
    }
};

• 时间复杂度：O(n)，其中 n 为数组的长度。每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。

• 空间复杂度：O(1)

解法2：额外数组

思路：使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k) %n 的位置，最后将新数组拷贝至原数组即可。

class Solution {
public:
    void rotate(vector& nums, int k) {
        int n = nums.size();
        vector newArr(n);
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        nums.assign(newArr.begin(), newArr.end());
    }
};

• 时间复杂度：O(n)，其中 n 为数组的长度。

• 空间复杂度：O(n)

31.寻找数组的中心下标  

 解法1：前缀和

class Solution {
public:
    int pivotIndex(vector& nums) {
        int sum=0;
        int leftSum=0,rightSum=0;
        for(const auto&num:nums) sum+=num;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 为数组的长度。

• 空间复杂度：O(1)。

32.按奇偶排序数组

 解法1：双指针

class Solution {
public:
    vector sortArrayByParity(vector& nums) {
        int n=nums.size();
        int left=0,right=n-1;
        while(leftnums[right]%2){
                int tmp=nums[left];
                nums[left]=nums[right];
                nums[right]=tmp;
            }
            if(nums[left]%2==0)left++;
            if(nums[right]%2==1)right--;
        }
        return nums;
    }
};

• 时间复杂度：O(n)，其中 n 是 nums 的长度。
• 空间复杂度：O(1)，不需要额外空间。

解法2：两次遍历

class Solution {
public:
    vector sortArrayByParity(vector& nums) {
        int n=nums.size(),t=0;
        vector ans(n);
        for(int x:nums){
            if(x%2==0){
                ans[t++]=x;
            }
        }
        for(int y:nums){
            if(y%2==1){
                ans[t++]=y;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是 nums 的长度。
• 空间复杂度：O(1)，注意在这里我们不考虑输出数组的空间占用。

33.按奇偶排序数组II

解法1：双指针

class Solution {
public:
    vector sortArrayByParityII(vector& nums) {
        int n=nums.size();
        int j=1;  // j指针用于遍历奇数位置的数
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是 nums 的长度。
• 空间复杂度：O(1)。

解法2：两次遍历

class Solution {
public:
    vector sortArrayByParityII(vector& nums) {
        int n=nums.size();
        int i=0,j=1;
        vector ans(n);
        for(int x:nums){
            if(x%2==0){
                ans[i]=x;
                i+=2;
            }
        }
        for(int y:nums){
            if(y%2==1){
                ans[j]=y;
                j+=2;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是 nums 的长度。
• 空间复杂度：O(1)，注意在这里我们不考虑输出数组的空间占用。

34.#调整数组顺序使奇数位于偶数前面

 解法1：双指针

class Solution {
public:
    vector exchange(vector& nums) {
        int n=nums.size();
        int left=0,right=n-1;
        while(leftnums[left]%2){
                int tmp=nums[right];
                nums[right]=nums[left];
                nums[left]=tmp;
            }
            if(nums[left]%2==1) left++;
            if(nums[right]%2==0) right--;
        }
        return nums;
    }
};

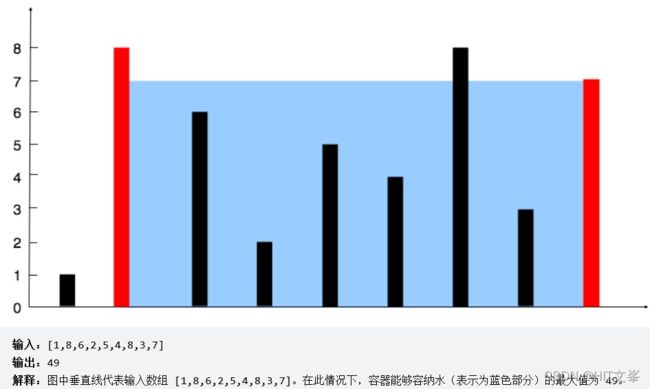
35.*盛最多水的容器

 解法1：前后指针

class Solution {
public:
    int maxArea(vector& height) {
        int n=height.size();
        int ans=0,i=0,j=n-1;
        while(i

• 时间复杂度：O(n)，双指针总计最多遍历整个数组一次。
• 空间复杂度：O(1)，只需要额外的常数级别的空间。

36.*颜色分类

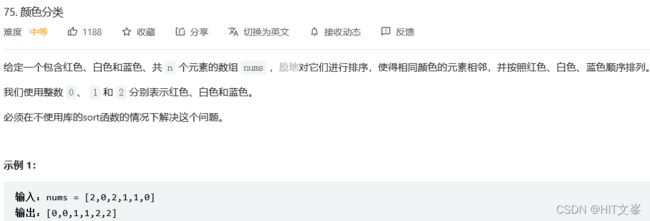解法1：单指针

class Solution {     //荷兰国旗问题
public:
    void sortColors(vector& nums) {
        int ptr=0;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。
• 空间复杂度：O(1)，只需要额外的常数级别的空间。

解法2：前后指针

class Solution {     //荷兰国旗问题
public:
    void sortColors(vector& nums) {
        int n=nums.size();
        int left=0,right=n-1;
        for(int i=0;i

37.*多数元素

解法1：哈希

class Solution {   //哈希表：快速统计每个元素出现的次数。键表示一个元素，值表示该元素出现的次数
public:
    int majorityElement(vector& nums) {
        unordered_map counts;
        int ans=0,n=nums.size();
        for(const int num:nums){
            ++counts[num];  //表示value增加
            if(counts[num]>n/2){
                ans=num;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。我们遍历数组 nums 一次，对于 nums 中的每一个元素，将其插入哈希表都只需要常数时间。
• 空间复杂度：O(n)，哈希表最多包含 n−n/2 个键值对，所以占用的空间为 O(n)。

解法2：排序

 思路：如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为 n/2 的元素（下标从 0 开始）一定是众数。

class Solution {
public:
    int majorityElement(vector& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

• 时间复杂度：O(nlog⁡n)，将数组排序的时间复杂度为 O(nlog⁡n)。
• 空间复杂度：O(log⁡n)，如果使用语言自带的排序算法，需要使用 O(log⁡n) 的栈空间。如果自己编写堆排序，则只需要使用 O(1) 的额外空间。

解法3：Boyer-Moore投票算法

 思路：如果我们把众数记为 +1，把其他数记为 −1，将它们全部加起来，和大于 0，从结果本身我们可以看出众数比其他数多。

class Solution {
public:
    int majorityElement(vector& nums) {
        int ans=-1;
        int count=0;  //count 的值一直为非负
        for(int num:nums){
            if(num==ans){
                ++count;
            }else if(--count<0){
                ans=num;
                count=1;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，Boyer-Moore 算法只对数组进行了一次遍历。
• 空间复杂度：O(1)，Boyer-Moore 算法只需要常数级别的额外空间。

38.#数组中出现次数超过一半的数字

解法1：哈希

class Solution {   //哈希表：快速统计每个元素出现的次数。键表示一个元素，值表示该元素出现的次数
public:
    int majorityElement(vector& nums) {
        unordered_map counts;
        int ans=0,n=nums.size();
        for(const int num:nums){
            ++counts[num];  //表示value增加
            if(counts[num]>n/2){
                ans=num;
            }
        }
        return ans;
    }
};

解法2：排序

class Solution {
public:
    int majorityElement(vector& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

39.*除自身以外数组的乘积

解法1：前后缀

 思路：所有数字的乘积除以给定索引处的数字，如果索引有0，则错误。而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。

前缀：索引左侧所有数字的乘积。后缀：索引右侧所有数字的乘积。

class Solution {
public:
    vector productExceptSelf(vector& nums) {
        int len=nums.size();
        vector L(len),R(len),ans(len);
        //前缀
        L[0]=1;
        for(int i=1;i=0;--i){
            R[i]=R[i+1]*nums[i+1];
        }
        // 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 O(n) 的时间复杂度。
• 空间复杂度：O(n)。使用了 L 和 R 数组去构造答案，L 和 R 数组的长度为数组 nums 的大小。

解法2：前后缀（优化空间）

优化：先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果 

class Solution {
public:
    vector productExceptSelf(vector& nums) {
        int len=nums.size();
        vector ans(len);
        //ans[i]  表示索引 i 左侧所有元素的乘积
        ans[0]=1;
        for(int i=1;i=0;--i){
            ans[i]=ans[i]*R; // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
            R*=nums[i]; 
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 O(n) 的时间复杂度。
• 空间复杂度：O(1)，输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。

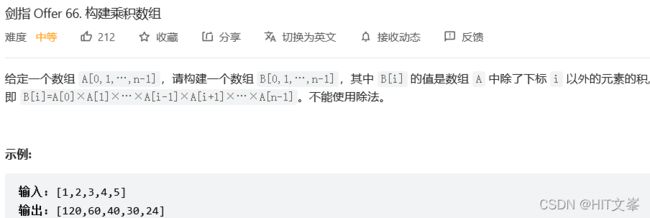
40.#构建乘积数组

 解法1：前后缀

class Solution {
public:
    vector constructArr(vector& a) {
        int n=a.size();
        if(n==0) return {};
        vector L(n);
        L[0]=1;
        for(int i=1;i=0;--i){
            L[i]=L[i]*R;
            R*=a[i];
        }
        return L;
    }
};

41.*寻找重复数

 解法1：快慢指针+同速指针

思路：（数组转链表的映射）对 nums 数组建图，每个位置 i 连一条 i→nums[i] 的边。由于存在的重复的数字 target，因此 target 这个位置一定有起码两条指向它的边，因此整张图一定存在环，且我们要找到的 target 就是这个环的入口，那么整个问题就等价于 142.环形链表 II。

1.数组中有一重复的整数 <==> 链表中存在环
2.找到数组中的重复整数 <==> 找到链表的环入口

可推出： 链表中慢指针走一步 slow = slow.next ==> 本题 slow = nums[slow]
               链表中快指针走两步 fast = fast.next.next ==> 本题 fast = nums[nums[fast]]

class Solution {    //快慢指针+同速指针
public:
    int findDuplicate(vector& nums) {
        int slow=0,fast=0;
        //快慢指针
        do{
            slow=nums[slow];
            fast=nums[nums[fast]];
        }while(slow!=fast);
        //同速指针
        slow=0;
        while(slow!=fast){
            slow=nums[slow];
            fast=nums[fast];
        }
        return slow;
    }
};

• 时间复杂度：O(n)，其中 n 指的是数组 nums 的大小。
• 空间复杂度：O(1)，我们只需要常数的空间存放变量。

解法2：二分查找

思路：抽屉原理：把 10 个苹果放进 9 个抽屉，一定存在某个抽屉放至少 2 个苹果。

统计原始数组中 小于等于 mid 的元素的个数 cnt： 如果 cnt 严格大于 mid。根据抽屉原理，重复元素就在区间 [left..mid] 里；否则，重复元素就在区间 [mid + 1..right] 里。

class Solution {
public:
    int findDuplicate(vector& nums) {
        int n = nums.size();
        int left = 1, right = n - 1, ans = -1;
        while (left <= right) {
            int mid = left+(right-left)/2;
            int cnt = 0;
            for (int num:nums) {
                if(num<=mid) cnt++;
            }
            if (cnt <= mid) {
                left = mid + 1;
            } else {
                right = mid - 1 ; 
                ans = mid;  //注意
            }
        }
        return ans;
    }
};

• 时间复杂度：O(nlog⁡n)，其中 n 为 nums 数组的长度。二分查找最多需要二分 O(log⁡n) 次，每次判断的时候需要O(n)遍历 nums 数组求解小于等于 mid 的数的个数，因此总时间复杂度为 O(nlog⁡n)。
• 空间复杂度：O(1)，我们只需要常数的空间存放变量。

42.#数组中重复的数字

 

解法1：哈希

class Solution {
public:
    int findRepeatNumber(vector& nums) {
        unordered_map hashtable;
        for(int num:nums){
            if(hashtable[num]) return num;
            hashtable[num]=true;
        }
        return -1;
    }
};

解法2：原地修改

class Solution {
public:
    int findRepeatNumber(vector& nums) {
        int i=0;
        while(i

43.*最短无序连续子数组

 解法1：排序+前后指针

思路：原数组nums=nums1+nums2+nums3  =>   nums1和nums3有序，nums2无序。寻找最短nums2,就是寻找最长 nums1+nums3 的长度。

class Solution {
public:
    int findUnsortedSubarray(vector& nums) {
        //当原数组有序时，nums2​ 的长度为 0，我们可以直接返回结果。
        if(is_sorted(nums.begin(),nums.end())){
            return 0;
        }
        vector numsSorted(nums);
        sort(numsSorted.begin(),numsSorted.end());
        int left=0,right=nums.size()-1;
        while(nums[left]==numsSorted[left]){
            left++;
        }
        while(nums[right]==numsSorted[right]){
            right--;
        }
        return right-left+1;
    }
};

• 时间复杂度：O(n)，其中 n 为给定数组的长度。我们需要 O(nlog⁡n) 的时间进行排序，以及 O(n) 的时间遍历数组，因此总时间复杂度为 O(n)。
• 空间复杂度：O(n)，其中 n 为给定数组的长度。我们需要额外的一个数组保存排序后的数组 numsSorted。

解法2：排序（优化空间）

 思路：原数组nums=nums1+nums2+nums3    =>   nums3 中任意一个数都大于nums1和nums2中的任意一个数，nums1 中任意一个数都小于nums2和nums3中的任意一个数。

class Solution {
public:
    int findUnsortedSubarray(vector& nums) {
        int n = nums.size();
        int maxn = INT_MIN, right = -1;
        int minn = INT_MAX, left  = -1;
        for (int i = 0; i < n; i++) {
            if (maxn > nums[i]) {
                right = i;
            } else {
                maxn = nums[i];
            }
            if (minn < nums[n - i - 1]) {
                left = n - i - 1;
            } else {
                minn = nums[n - i - 1];
            }
        }
        return right == -1 ? 0 : right - left + 1;
    }
};

• 时间复杂度：O(n)，其中 n 为给定数组的长度。我们仅需要遍历该数组一次。
• 空间复杂度：O(1)，只需要常数的空间保存若干变量。

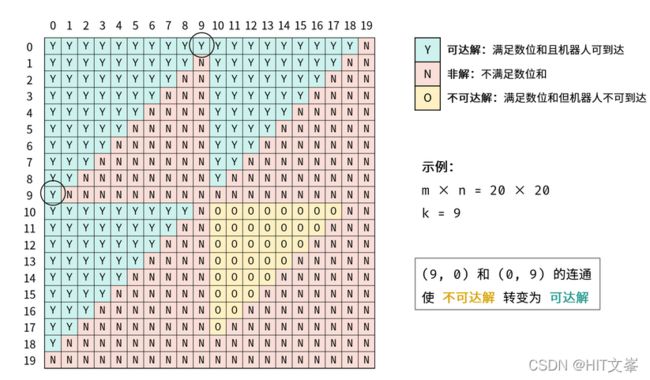
44.#机器人的运动范围

 思路：根据可达解的结构和连通性，易推出机器人可 仅通过向右和向下移动，访问所有可达解 。

 

解法1：深度优先搜索

class Solution {
private:
    int get(int x){//求数位之和
        int sum=0;
        while(x){
            sum+=x%10;
            x=x/10;
        }
        return sum;
    }
    int dfs(int i, int j, int si, int sj, vector> &visited, int m, int n, int k) {
        if(i >= m || j >= n || si + sj >k || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, get(i+1), sj, visited, m, n, k) +
                   dfs(i, j + 1, si, get(j+1), visited, m, n, k);
    }
public:
    int movingCount(int m, int n, int k) {
        vector> visited(m, vector(n, 0));
        return dfs(0, 0, 0, 0, visited, m, n, k);
    }   
};

45.Pow(x,n)

 

解法1：快速幂+递归

 思路：「快速幂算法」的本质是分治算法。当指数 n 为负数时，我们可以计算 x^{-n} 再取倒数得到结果，因此我们只需要考虑 n 为自然数的情况。从 x 开始，每次直接把上一次的结果进行平方，计算 6 次就可以得到 x^64 的值，而不需要对 x 乘 63 次 x。

我们从右往左看，分治的思想：（1）当我们要计算 x^n 时，我们可以先递归地计算出 y=x^[n/2]，其中 [ a ] 表示对 a 进行下取整；（2）根据递归计算的结果，如果 n 为偶数，那么 x^n = y^2；如果 n 为奇数，那么 x^n = y^2 ×x；（3） 递归的边界为 n=0，任意数的 0 次方均为 1。

class Solution {
private:
    double quickPow(double x,long n){
        if(n==0) return 1.0;
        double y=quickPow(x,n/2);
        return n%2==0 ? y*y : y*y*x;
    }
public:
    double myPow(double x, int n) {
        long m=n;
        return m>=0 ? quickPow(x,m) : 1.0/quickPow(x,-m);
    }
};

• 时间复杂度：O(log⁡n)，即为递归的层数。
• 空间复杂度：O(logn)，即为递归的层数。这是由于递归的函数调用会使用栈空间。

解法2：快速幂+迭代

 

class Solution {
private:
    double quickPow(double x,long n){
        double ans=1.0;
        // 在对 n 进行二进制拆分的同时计算答案
        while(n>0){
            if(n%2==1){// 如果 n 二进制表示的最低位为 1，那么需要计入贡献
                ans*=x;
            }
            x*=x;     // 将贡献不断地平方
            n/=2;     // 舍弃 n 二进制表示的最低位，这样我们每次只要判断最低位即可
        }
        return ans;
    }
public:
    double myPow(double x, int n) {
        long m=n;
        return m>=0 ? quickPow(x,m) : 1.0/quickPow(x,-m);
    }
};

• 时间复杂度：O(log⁡n)，即为对 n 进行二进制拆分的时间复杂度。
• 空间复杂度：O(1)，只需要常数的空间保存若干变量。

46.#数值的整数次方

 

解法1：快速幂+递归

class Solution {
private:
    double quickPow(double x,long n){
        if(n==0) return 1.0;
        double y=quickPow(x,n/2);
        return n%2==0 ? y*y : y*y*x;
    }
public:
    double myPow(double x, int n) {
        long m=n;
        return m>=0 ? quickPow(x,m) : 1.0/quickPow(x,-m);
    }
};

解法2：快速幂+迭代

class Solution {
private:
    double quickPow(double x,long n){
        double ans=1.0;
        // 在对 n 进行二进制拆分的同时计算答案
        while(n>0){
            if(n%2==1){// 如果 n 二进制表示的最低位为 1，那么需要计入贡献
                ans*=x;
            }
            x*=x;     // 将贡献不断地平方
            n/=2;     // 舍弃 n 二进制表示的最低位，这样我们每次只要判断最低位即可
        }
        return ans;
    }
public:
    double myPow(double x, int n) {
        long m=n;
        return m>=0 ? quickPow(x,m) : 1.0/quickPow(x,-m);
    }
};

47.#扑克牌中的顺子

 

解法1：排序+遍历

思路：排序后，数组末位元素 nums[4] 为最大牌；元素 nums[joker] 为最小牌，其中 joker 为大小王的数量。

class Solution {
public:
    bool isStraight(vector& nums) {
        int joker=0;
        sort(nums.begin(),nums.end());
        for(int i=0;i<4;++i){
            if(nums[i]==0) joker++;// 统计大小王数量
            else if(nums[i]==nums[i+1]) return false;// 若有重复，提前返回 false
        }
        return nums[4]-nums[joker]<5;// 最大牌 - 最小牌 < 5 则可构成顺子
    }
};

• 时间复杂度：O(nlogn)=O(5log⁡5)=O(1)，其中 n 为 nums 长度，本题中 n=5 ；数组排序使用 O(nlogn) 时间。

• 空间复杂度：O(1)，变量 joker 使用 O(1) 大小的额外空间。

解法2：哈希

class Solution {
public:
    bool isStraight(vector& nums) {
        unordered_set hashtable;
        int mx=INT_MIN,mn=INT_MAX;
        for(int num:nums){
            if(num==0) continue;// 跳过大小王
            mx=max(mx,num);  // 最大牌
            mn=min(mn,num);  // 最小牌
            if(hashtable.count(num)) return false; // 若有重复，提前返回 false
            hashtable.insert(num);
        }
        return mx-mn<5;
    }
};

48.#圆圈中最后剩下的数字 （约瑟夫环）

 解法1：数学+递归

思路：由于我们删除了第 m % n 个元素，将序列的长度变为 n - 1。当我们知道了 f(n - 1, m) 对应的答案 x 之后，我们也就可以知道，长度为 n 的序列最后一个删除的元素，应当是从 m % n 开始数的第 x 个元素。因此有 f(n, m) = (m % n + x) % n = (m + x) % n。

class Solution {
private:
    int f(int n,int m){
        if(n==1) return 0;
        int x=f(n-1,m);
        return (x+m)%n;
    }
public:
    int lastRemaining(int n, int m) {
        return f(n,m);
    }
};

• 时间复杂度：O(n)，需要求解的函数值有 n 个。

• 空间复杂度：O(n)，函数的递归深度为 n，需要使用 O(n) 的栈空间。

解法2：动态规划

class Solution {
public:
    int lastRemaining(int n, int m) {
        int f=0;
        for(int i=2;i<=n;++i){
            f=(f+m)%i;
        }
        return f;
    }
};

• 时间复杂度：O(n)， 状态转移循环 n−1 次使用 O(n) 时间，状态转移方程计算使用 O(1) 时间。

• 空间复杂度：O(1)，使用常数大小的额外空间。

49.合并两个有序数组

解法1：双指针

class Solution {
public:
    void merge(vector& nums1, int m, vector& nums2, int n) {
        int p1=0,p2=0;
        int cur=0;
        vector sorted(m+n);
        while(p1

50.重复至少K次且长度为M的模式

 解法1：暴力

思路：找到一个连续出现 k 次且长度为 m 的子数组。也就是说如果这个子数组的左端点是 i，那么对于任意 j∈[0,m×k)，都有 a[i+j]=a[i+j%m]。因此，我们可以枚举左端点 i，对于每个 i 枚举 j∈[0,m×k)，判断是否满足条件即可。

class Solution {
public:
    bool containsPattern(vector& arr, int m, int k) {
        int n=arr.size();
        for(int i=0; i <= n-m*k;++i){
            int j=0;
            for(;j

• 时间复杂度：O(nmk)，最外层循环 i 的取值个数为 n−m×k，内层循环 j 的取值个数为 m×k，故渐进时间复杂度为 O((n−m×k)×m×k)=O(nmk)。

• 空间复杂度：O(1)

51.@统计数组中峰和的数量

 解法1：前后遍历

class Solution {
public:
    int countHillValley(vector& nums) {
        int res = 0;   // 峰与谷的数量
        int n = nums.size();
        for (int i = 1; i < n - 1; ++i) {
            if (nums[i] == nums[i-1]) {
                // 去重
                continue;
            }

            //  1 代表邻居大于该元素，−1 代表邻居小于该元素，0 代表未找到或不存在该方向的不相等邻居
            int left = 0;   // 左边可能的不相等邻居对应状态
            for (int j = i - 1; j >= 0; --j) {
                if (nums[j] > nums[i]) {
                    left = 1;
                    break;
                } else if (nums[j] < nums[i]) {
                    left = -1;
                    break;
                }
            }
            int right = 0;   // 右边可能的不相等邻居对应状态
            for (int j = i + 1; j < n; ++j) {
                if (nums[j] > nums[i]) {
                    right = 1;
                    break;
                } else if (nums[j] < nums[i]) {
                    right = -1;
                    break;
                }
            }
            if (left == right && left != 0) {
                // 此时下标 i 为峰或谷的一部分:当且仅当 left=right 且 left≠0。
                ++res;
            }
        }
        return res;   
    }
};

• 时间复杂度：O(n^2)，其中 n 为 nums 的长度。对于每个元素，判断是否为峰或者谷的时间复杂度为 O(n)。

• 空间复杂度：O(1)

题型二：链表

 1.移除链表元素

解法1：迭代

思路：设置虚拟头结点dummyHead，使得在单链表中移除头结点 和 移除其他节点的操作方式是一样的。return 头结点的时候，别忘了 return dummyHead->next;， 这才是新的头结点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
         //因为 ListNode 是结构体， 头节点可能被删除，创建一个哑节点
         ListNode *dummyHead = new ListNode(0, head);     
         ListNode *temp = dummyHead;  //temp 表示当前节点

         while(temp->next != NULL){
             //如果 temp 的下一个节点不为空且下一个节点的节点值等于给定的 val，则需要删除下一个节点。
             if(temp->next->val ==val){
                 temp->next = temp->next->next; // 迭代删除
             }else{
                 temp=temp->next;               // 保留
             }
         }
         return dummyHead->next;               // 返回删除操作后的头节点
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次

• 空间复杂度：O(1)

解法2：递归

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
         if (head==nullptr){
             return head;
         }
         head->next = removeElements(head->next,val);    //递归删除
         //最后判断 head 的节点值是否等于 val 并决定是否要删除 head
         return head->val == val?head->next:head;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次

• 空间复杂度：O(n)，空间复杂度主要取决于递归调用栈，最多不会超过 n 层

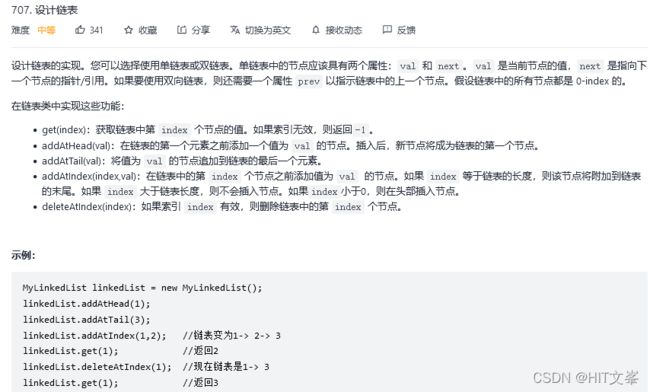
2.设计链表

 解法1：单链表

class MyLinkedList {
private:
    struct LinkedNode {    // 定义链表节点结构体
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val),next(nullptr){}
    };
    int size;
    LinkedNode *dummyHead;
public:
    //单链表是最简单的链表，双链表是最常用的链表
    //哨兵节点：在树和链表中被广泛的用作伪头、伪尾，通常不保存任何数据
    
    //初始化链表
    MyLinkedList(){
      dummyHead = new LinkedNode(0) ;  //定义一个哨兵节点
      size=0;
    }

    // 1、获取链表中第 index 个节点的值。如果索引无效，则返回-1。
    // 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if(index>(size-1)||index<0){
            return -1;
        }
        LinkedNode *temp = dummyHead->next;
        while(index--){   //--index 会陷入死循环
            temp=temp->next;
        }
        return temp->val;
    }
    
    // 2、在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
    void addAtHead(int val) {
         LinkedNode *newNode = new LinkedNode(val);

         newNode->next=dummyHead->next;
         dummyHead->next=newNode;

         size++;
    }
    
    // 3、将值为 val 的节点追加到链表的最后一个元素。
    void addAtTail(int val) {
         LinkedNode *newNode = new LinkedNode(val);

         LinkedNode *temp = dummyHead;
         while(temp->next !=nullptr){
             temp = temp->next;
         }
         temp->next = newNode;

         size++;
    }
    
    // 4、在链表中的第 index 个节点之前添加值为 val  的节点。
    //   如果 index 等于链表的长度，则该节点将附加到链表的末尾。
    //   如果 index 大于链表长度，则不会插入节点。
    //   如果index小于0，则在头部插入节点。
    void addAtIndex(int index, int val) {
        if(index>size){
            return;
        }

        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* temp = dummyHead;

        while(index--) {
            temp = temp->next;
        }
        newNode->next = temp->next;
        temp->next = newNode;

        size++;
    }
    
    // 5、如果索引 index 有效，则删除链表中的第 index 个节点。
    void deleteAtIndex(int index) {

         if (index >= size || index < 0) {
            return;
        }

        LinkedNode* cur = dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* temp = cur->next;
        cur->next = cur->next->next;
        delete temp;
        size--;
    }
};

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList* obj = new MyLinkedList();
 * int param_1 = obj->get(index);
 * obj->addAtHead(val);
 * obj->addAtTail(val);
 * obj->addAtIndex(index,val);
 * obj->deleteAtIndex(index);
 */

• 时间复杂度：

         addAtHead： O(1)
         addAtIndex，get，deleteAtIndex: O(k)，其中 k 指的是元素的索引。
         addAtTail：O(n)，其中 n 指的是链表的元素个数

• 空间复杂度：O(1)，所有的操作都是。

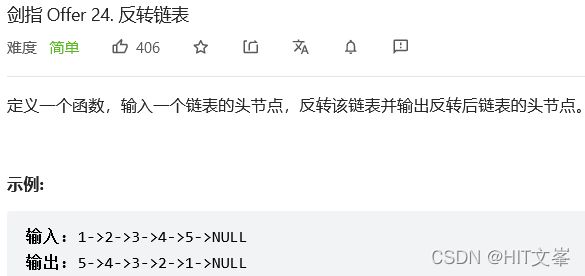
3.*反转链表

 

解法1：迭代

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *prev=nullptr;
        ListNode *cur=head;

        while(cur){
            // tmp 保存一下 cur 的下一个节点，因为接下来要改变cur->next
            ListNode *tmp = cur->next;  
            cur->next =prev;      // 翻转操作

            // 更新prev 和 cur指针
            prev=cur;
            cur=tmp;
        }
        return prev;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次

• 空间复杂度：O(1)

 解法2：递归

从后往前翻转指针指向 

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 边缘条件判断
        if(!head||!head->next){
            return head;
        }
        // 1、递归调用，翻转第二个节点开始往后的链表
        ListNode *newHead = reverseList(head->next);
        // 2、翻转头节点与第二个节点的指向
        head->next->next=head;     // 翻转第二个节点的指向 
        head->next=nullptr;        // n1的下一个节点必须指向空，否则链表会变成环
        return newHead;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作

• 空间复杂度：O(n)，空间复杂度主要取决于递归调用栈，最多不会超过 n 层

4.#反转链表

 解法1：迭代

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre=NULL,*cur=head;
        while(cur){
            ListNode *tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        return pre;
    }
};

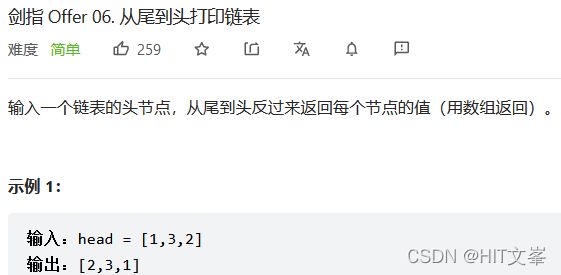
5.#从尾到头打印链表

解法1：迭代

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };*/
class Solution {
public:
    vector reversePrint(ListNode* head) {
        ListNode *pre=NULL,*cur=head;
        while(cur){
            ListNode *tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        vector ans;
        while(pre){
            ans.push_back(pre->val);
            pre=pre->next;
        }
        return ans;
    }
};

解法2：栈

class Solution {
public:
    vector reversePrint(ListNode* head) {
        stack stk;
        vector ans;
        while(head){
            stk.push(head->val);
            head=head->next;
        }
        while(!stk.empty()){
            ans.push_back(stk.top());
            stk.pop();
        }
        return ans;
    }
};

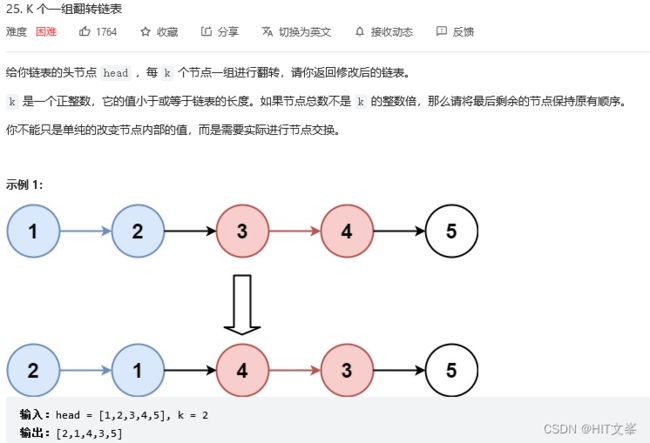
6.K个一组翻转链表

 解法1：模拟

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    // 翻转一个子链表，并且返回新的头与尾
    pair myReverve(ListNode* head, ListNode* tail){
        ListNode* prev=tail->next;
        ListNode* p=head;
        while(prev!=tail){
            ListNode* tmp=p->next;
            p->next=prev;
            prev=p;
            p=tmp;
        }
        return {tail,head};
    }
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode *dummyHead=new ListNode(0,head);
        ListNode *pre=dummyHead;
        while(head){
            ListNode* tail=pre;
            // 查看剩余部分长度是否大于等于 k
            for(int i=0;inext;
                if(tail==nullptr){
                    return dummyHead->next;
                }
            }
            ListNode *tmp=tail->next;
            pair ret=myReverve(head,tail);
            head=ret.first;
            tail=ret.second;

            // 把子链表重新接回原链表
            pre->next=head;
            tail->next=tmp;

            pre=tail;
            head=tail->next;
        }
        return dummyHead->next;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。head 指针会在 O(⌊n/k⌋)个节点上停留，每次停留需要进行一次 O(k) 的翻转操作。

• 空间复杂度：O(1)，我们只需要建立常数个变量。

7.*回文链表

解法1：数组模拟+前后指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        ListNode *tmp=head;
        vector vec;
        //将链表回文 转化为 数组回文
        while(tmp){
            vec.push_back(tmp->val);
            tmp=tmp->next;
        }
        for(int i=0,j=vec.size()-1;i

• 时间复杂度：O(n)，其中 n 是链表的节点数。第一步： 遍历链表并将值复制到数组中，O(n)。第二步：双指针判断是否为回文，执行了 O(n/2) 次的判断，即 O(n)。总的时间复杂度：O(2n)=O(n)。

• 空间复杂度：O(n)，其中 n 是链表的节点数。我们使用了一个数组列表存放链表的元素值。

解法2：快慢指针

思路：整个流程可以分为以下五个步骤：（1）找到前半部分链表的尾节点。（2）反转后半部分链表。（3）判断是否回文。（4）恢复链表。（5）返回结果。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if(head==nullptr) return true;
        ListNode* fast=head;
        ListNode* slow=head;
        ListNode* node=head;   //记录慢指针的前一个节点，用来分割链表
        while(fast && fast->next){
            node=slow;
            slow=slow->next;
            fast=fast->next->next;
        }
        node->next=nullptr; // 分割链表
        // 判断是否回文
        ListNode* p1=head;
        ListNode* p2=reverseList(slow);// 反转后半部分，总链表长度如果是奇数，p2比p1多一个节点
        while(p1){
            if(p1->val!=p2->val) return false;
            p1=p1->next;
            p2=p2->next;
        }
        return true;
    }   
    //反转链表
    ListNode* reverseList(ListNode* head){
        ListNode* pre=nullptr;
        ListNode* cur=head;
        while(cur){
            ListNode* tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        return pre;
    }   
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。

• 空间复杂度：O(1)，其中 n 是链表的节点数。我们只会修改原本链表中节点的指向，而在堆栈上的堆栈帧不超过 O(1)。

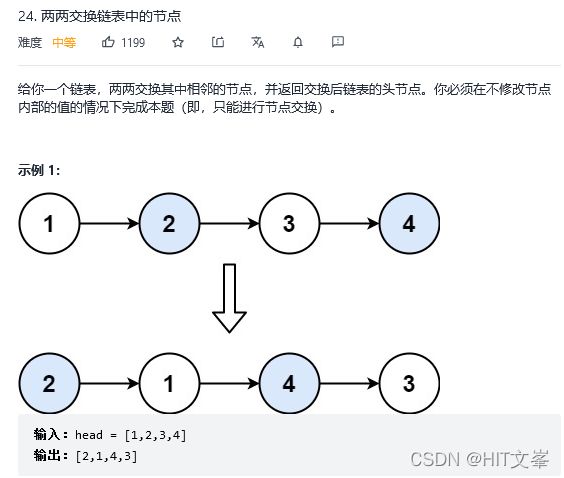
8.两两交换链表中的节点

 解法1：迭代

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {      
        ListNode *dummyHead=new ListNode(0);//设置一个哑指针dummyHead
        dummyHead->next=head;
        ListNode *tmp=dummyHead;   //表示当前到达的节点
        //如果 temp 的后面没有节点或者只有一个节点，则没有更多的节点需要交换，因此结束交换。
        //此处不能是||，只能是&&
        while(tmp->next!=nullptr&&tmp->next->next!=nullptr){ 
           //这两行放while外面会超出时间限制，因为放外面不一定存在
           ListNode *node1=tmp->next;
           ListNode *node2=tmp->next->next;

            //交换node1和node2的位置，3步骤不能颠倒顺序
            tmp->next=node2;
            node1->next=node2->next; //重要
            node2->next=node1;

            //移动哑指针位置，准备下一次交换
            tmp=node1;
        }
        return  dummyHead->next;    //tmp->next是错误代码
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数量。需要对每个节点进行更新指针的操作

• 空间复杂度：O(1)

 解法2：递归

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    //head表示原始链表的头节点，新链表的第二个节点
    //newHead 表示原始链表的第二个节点，新链表的头节点
    ListNode* swapPairs(ListNode* head) {  
        //如果链表没有节点，或只有一个节点，则不能交换
       if(head==nullptr||head->next==nullptr){
           return head;
       }

       ListNode *newHead=head->next; 
       //将剩余的节点进行两两交换
       //newHead->next 是原始链表的其余节点的头节点，head->next是交换后的新的头节点
       head->next=swapPairs(newHead->next); 
       newHead->next=head;     //完成所有交换
       return newHead;     //返回新链表的头节点
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数量。需要对每个节点进行更新指针的操作

• 空间复杂度：O(n)，空间复杂度主要取决于递归调用的栈空间

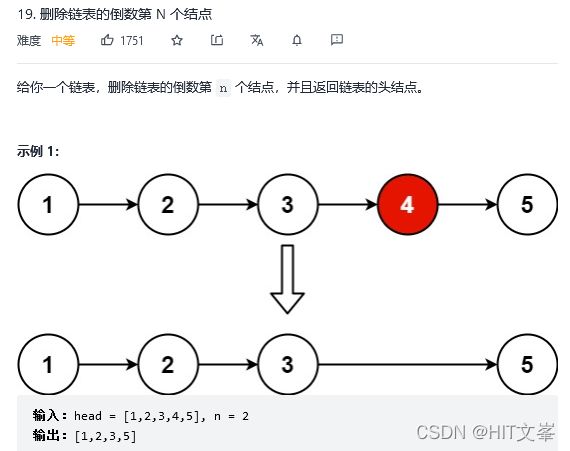
9.*删除链表的倒数第N个节点

 

 解法1：快慢指针

思路：如果要删除倒数第n个节点，先让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾，最后删除slow指向的下一个节点即可

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
          ListNode *dummyHead = new ListNode(0);    //链表经常使用到哑节点
          dummyHead->next=head;
          //注意快慢指针的起始位置不同，首先让快指针先走n个单位，两个指针相距n
          ListNode *fast = head;
          ListNode *slow = dummyHead;
          for(int i=0;inext;
          }
          
          while(fast){   //直到快指针指向空
              fast=fast->next;
              slow=slow->next;
          }
          slow->next=slow->next->next;  //删除slow指向的下一个节点   
          return dummyHead->next;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度

• 空间复杂度：O(1)

解法2：计算链表长度

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
private:
    //首先遍历一遍链表，得到链表的长度
    int getLength(ListNode *head){
        int length =0;
        while(head){
            ++length;
            head=head->next;
        }
        return length;
    }
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
          ListNode *dummyHead = new ListNode(0,head);
          ListNode *tmp =dummyHead;
          int length = getLength(head);
          for(int i=1;inext;  // tmp 移动 length-n 步，此时指向第 length-n 个节点
          } 
          tmp->next=tmp->next->next;
          //ListNode *ans=dummyHead->next;   //为了删除哑节点，首先存储
          //delete dummyHead;   //释放被删除节点对应的空间
          //return ans;
          return dummyHead->next;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度

• 空间复杂度：O(1)

 解法3：栈

思路：在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
          ListNode *dummyHead = new ListNode(0,head);
          ListNode *tmp =dummyHead;          
          stack stk;
          //1、链表中元素全部入栈
          while(tmp){
              stk.push(tmp);
              tmp=tmp->next;
          }
          //2、删除栈顶前n个元素
          for(int i=0;inext=prev->next->next;
     
          return dummyHead->next;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度

• 空间复杂度：O(n)，其中 n 是链表的长度，主要是栈的开销

10.&输出单向链表中倒数第K个节点

 

 解法1：双指针

#include
#include
using namespace std;
struct ListNode{
    int val;
    ListNode* next;
    ListNode(int x):val(x),next(nullptr){};
};

ListNode* getKthFromEnd(ListNode* head,int k){
        ListNode* dummyHead=new ListNode(-1);
        dummyHead->next=head;
        ListNode *slow=dummyHead;
        ListNode *fast=head;
        for(int i=0;inext;
        }
        while(fast){
            slow=slow->next;
            fast=fast->next;
        }
        return slow->next;
}

int main(){
    int n;
    while(cin>>n){  // 1、输入链表节点个数n
        // 2、输入链表的值（构建链表）
        int val;
        cin>>val;
        
        ListNode *head=new ListNode(val);
        ListNode *p=head;
        for(int i=1;i>val;
            ListNode *q=new ListNode(val);
            p->next=q;  // 连接
            p=p->next;
        }
        
        // 3、输入k的值，使用快慢指针
        int k;
        cin>>k;
        if(k==0){
            cout << 0 <val << endl;
        }
    }
    return 0;
}

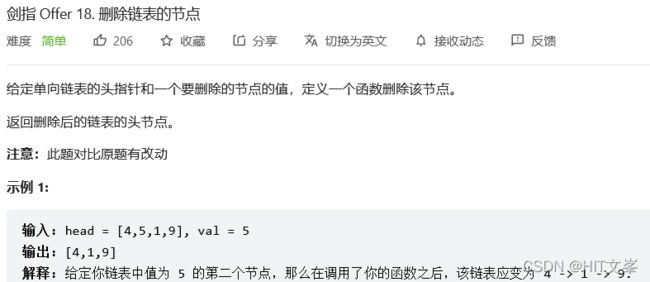
11.#删除链表的节点

 

解法1：快慢指针

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        ListNode* dummyHead=new ListNode(0,head);
        ListNode *slow=dummyHead,*fast=head;
        while(fast){          
            if(fast->val==val){
                slow->next=fast->next;
            }
            slow=fast;
            fast=fast->next;
        }
        return dummyHead->next;
    }
};

解法2：单指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        ListNode* dummyHead=new ListNode(0,head);
        ListNode* cur=dummyHead;
        while(cur->next!=NULL){
            if(cur->next->val==val){
                cur->next=cur->next->next;
                break;  //此处一定要暂停
            }
            cur=cur->next;
        }
        return dummyHead->next;
    }
};

12.#链表中倒数第k个节点

 

解法1：快慢指针

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode *dummyHead = new ListNode(0,head);    //链表经常使用到哑节点
        //注意快慢指针的起始位置不同，首先让快指针先走n个单位，两个指针相距n
        ListNode *fast= head;
        ListNode *slow =dummyHead;
        for(int i=0;inext;
        }          
        while(fast){   //直到快指针指向空
              fast=fast->next;
              slow=slow->next;
        } 
        return slow->next;
    }
};

解法2：求链表长度

class Solution {
private:
    int getLength(ListNode* head){
        int len=0;
        while(head){
            len++;
            head=head->next;
        }
        return len;
    }
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        int len=getLength(head);
        for(int i=1;inext;
        }
        return head;
    }
};

13.#链表相交

 解法1：双指针

思路：A长度为 a, B长度为b，假设存在交叉点，此时 A到交叉点距离为 c，而B到交叉点距离为d，后续交叉后长度是一样的，那么就是     a - c = b - d    =>     a + d = b + c
意味着只要分别让A和B额外多走一遍B和A，那么必然会走到交叉，注意，大家都走到null依然没交叉，那么正好返回null即可

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
         ListNode *a=headA;
         ListNode *b=headB;
         while(a!=b){
             a = a!=NULL   ?a->next:headB;
             b = b!=nullptr?b->next:headA;
         }  
         return a;
    }
};

• 时间复杂度：O(m+n)

• 空间复杂度：O(1)

解法2：求链表的长度

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */   
class Solution {   //题目不是找数值相同的指针，而是找后几位相同的链表
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != NULL) { // 求链表A的长度
            lenA++;
            curA = curA->next;
        }
        while (curB != NULL) { // 求链表B的长度
            lenB++;
            curB = curB->next;
        }
        curA = headA;
        curB = headB;

        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            swap (lenA, lenB);
            swap (curA, curB);
        }

        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap--) {
            curA = curA->next;
        }
        
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != NULL) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

• 时间复杂度：O(m+n)

• 空间复杂度：O(1)

14.*相交链表

 解法1：双指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };*/
class Solution {     //双指针：指针A先遍历headA，再遍历headB；指针B先遍历headB，再遍历headA
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA==NULL || headB==NULL){
            return NULL;
        }
        ListNode *pA=headA,*pB=headB;
        while(pA!=pB){
            pA = pA!=NULL ? pA->next : headB;
            pB = pB!=NULL ? pB->next : headA;
        }
        return pA;
    }
};

解法2：哈希

class Solution {    //哈希表：判断两个链表是否相交，可以使用哈希集合存储链表节点。
public:
    //链表headA先放入哈希表中，在用链表headB遍历，看有没有重复
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set visited;
        ListNode *node=headA;
        while(node!=NULL){
            visited.insert(node);
            node=node->next;
        }
        node=headB;
        while(node!=NULL){
            if(visited.count(node)){
                return node;
            }
            node=node->next;
        }
        return NULL;
    }
};

• 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。

• 空间复杂度：O(m)，其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。

15.#两个链表的第一个公共节点

 解法1：双指针

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA==NULL||headB==NULL) return NULL;
        ListNode *pA=headA,*pB=headB;
        while(pA!=pB){
            pA=pA!=NULL?pA->next:headB;
            pB=pB!=NULL?pB->next:headA;
        }     
        return pA;
    }
};

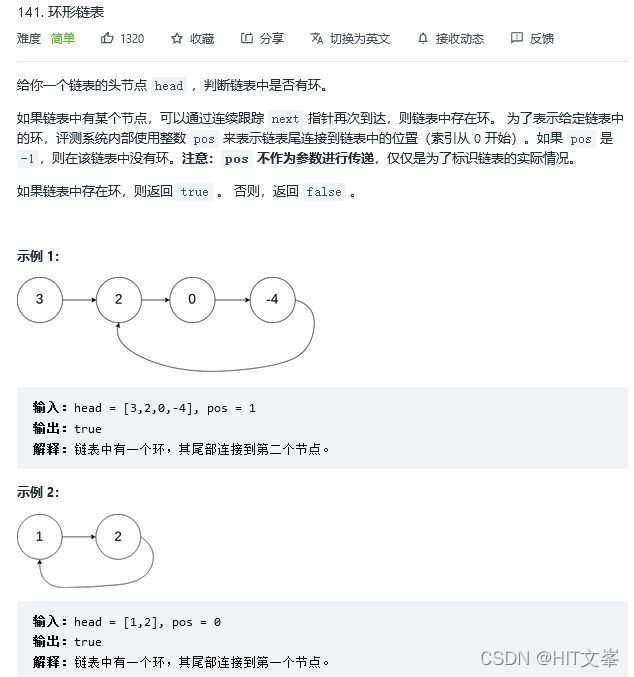
16.*环形链表

 

解法1：快慢指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
       ListNode *slow=head;
       ListNode *fast=head;
       while(fast!=NULL && fast->next!=NULL){
           // 快指针走两步，慢指针走一步：快慢指针相遇，说明有环
           slow=slow->next;
           fast=fast->next->next;
           if(slow==fast) return true;
       }
       return false;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。

• 空间复杂度：O(1)，我们只使用了两个指针的额外空间。

解法2：哈希

思路：哈希表来存储所有已经访问过的节点。每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set uset;
        while(head!=NULL){
            //count 返回关键字的数量：对于不允许重复关键字的容器，返回值永远是0或1
            if(uset.count(head)) return true;
            uset.insert(head);
            head=head->next;
        }
        return false;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。最坏情况下我们需要遍历每个节点一次。

• 空间复杂度：O(n)，其中 n 是链表的节点数。主要为哈希表的开销，最坏情况下我们需要将每个节点插入到哈希表中一次。

17.*环形链表II

解法1：快慢指针+同速指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast=head,*slow=head;     //构造快慢两个指针，起始均指向头节点

        while(fast!=nullptr && fast->next!=nullptr){
            fast=fast->next->next;          //快指针走的速度是慢指针的2倍
            slow=slow->next;

            if(fast==slow){
                //快慢指针第一次相遇后，从 头结点 出发一个指针node1，从 相遇节点 也出发一个指针node2，
                //这两个指针每次只走一个节点， 那么当这两个指针第二次相遇的时候就是 环形入口的节点
                ListNode *node1 = head;
                ListNode *node2 = slow;
                while(node1 != node2){
                    node1=node1->next;
                    node2=node2->next;
                }
                return node1;
            }
        }
        return nullptr;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。

  在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(n)+O(n)=O(n)

• 空间复杂度：O(1)，我们只使用了四个指针的额外空间。

解法2：哈希

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set visited;     //利用哈希表记录节点
        while(head != nullptr){

            if(visited.count(head)){      //遍历到重复的节点，则存在环
                return head;
            }

            visited.insert(head);     //遍历节点
            head=head->next;

        }
        return nullptr;
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。我们恰好需要访问链表中的每一个节点。

• 空间复杂度：O(n)，其中 n 是链表的节点数。主要为哈希表的开销，我们需要将链表中的每个节点都保存在哈希表当中。

18. 链表的中间节点

解法1：快慢指针

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* slow=head;
        ListNode* fast=head;
        while(fast && fast->next){
            slow=slow->next;
            fast=fast->next->next;
        }
        return slow;
    }
};

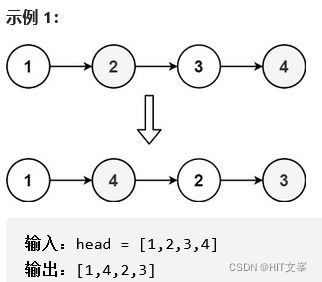
19.重排链表

 

 解法1：数组模拟+前后指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reorderList(ListNode* head) {
        vector vec;
        ListNode* node=head;
        while(node){
            vec.push_back(node);
            node=node->next;
        }
        int i=0,j=vec.size()-1; 
        while(inext=vec[j];
            i++;
            if(i==j) break;
            vec[j]->next=vec[i];
            j--;
        }
        vec[i]->next=nullptr;   //结尾指向空
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。

• 空间复杂度：O(n)，其中 n 是链表的节点数。主要为数组的开销。

 解法2：寻找链表中点 + 链表逆序 + 合并链表

class Solution {
public:
    void reorderList(ListNode* head) {
        if(head==nullptr) return;
        ListNode* mid=midNode(head);
        ListNode* node1=head;
        ListNode* node2=mid->next;
        mid->next=nullptr;
        node2=reverseList(node2);
        mergeList(node1,node2);
    }
    ListNode* midNode(ListNode* head){
        ListNode* slow=head;
        ListNode* fast=head;
        while(fast && fast->next){
            slow=slow->next;
            fast=fast->next->next;
        }
        return slow;
    }
    ListNode* reverseList(ListNode* head){
        ListNode* pre=nullptr;
        ListNode* cur=head;
        while(cur){
            ListNode* tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        return pre;
    }
    void mergeList(ListNode* p1,ListNode* p2){
        while(p1 && p2){
            ListNode* p1_tmp=p1->next;
            ListNode* p2_tmp=p2->next;
            p1->next=p2;
            p1=p1_tmp;
            p2->next=p1;
            p2=p2_tmp;
        }
    }
};

• 时间复杂度：O(n)，其中 n 是链表的节点数。

• 空间复杂度：O(1)。

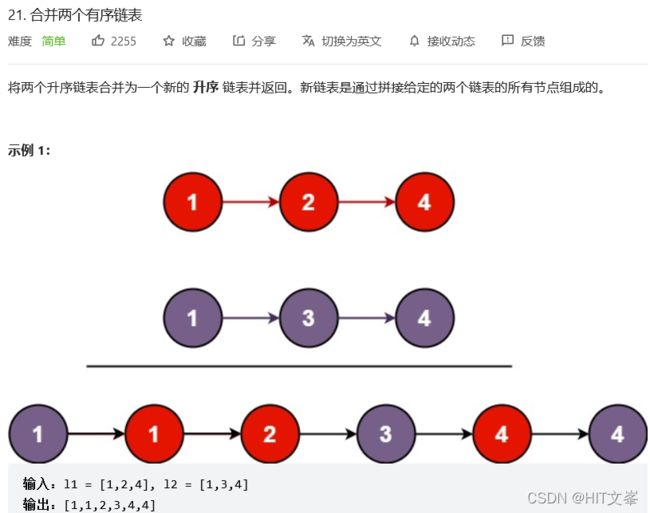
20.*合并两个有序链表

解法1：递归

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1==nullptr){
            return list2;
        }else if(list2==nullptr){
            return list1;
        }else if(list1->val < list2->val){
            list1->next=mergeTwoLists(list1->next,list2);
            return list1;
        }else{
            list2->next=mergeTwoLists(list1,list2->next);
            return list2;
        }
    }
};

• 时间复杂度：O(n+m)。因为每次调用递归都会去掉 l1 或者 l2 的头节点（直到至少有一个链表为空），函数 mergeTwoList 至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即 O(n+m)。

• 空间复杂度：O(n+m)。递归调用 mergeTwoLists 函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m 次，因此空间复杂度为 O(n+m)。

解法2：迭代

class Solution {   //迭代
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        // head 与 tail 分别代表合并链表的头部和尾部
        ListNode *head=new ListNode(-1);
        ListNode *tail=head;
        while(list1 && list2){  //两个链表都不为空
            if(list1->val < list2->val){
                tail->next=list1;
                list1=list1->next;
            }else{
                tail->next=list2;
                list2=list2->next;
            }
            tail=tail->next;   //不能忘
        }
        //至多有一个链表没有合并完，需要将链表剩余的部分加在合并链表的后面
        tail->next = (list1!=nullptr ? list1 : list2);
        return head->next;
    }
};

• 时间复杂度：O(n+m)。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。

• 空间复杂度：O(1)。我们只需要常数的空间存放若干变量。

21.#合并两个排序的链表

 

 解法1：迭代

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode *head=new ListNode(0);
        ListNode *tail=head;
        while(l1 && l2){
            if(l1->val < l2->val){
                tail->next=l1;
                l1=l1->next;
            }else{
                tail->next=l2;
                l2=l2->next;
            }
            tail=tail->next;
        }
        tail->next=(l1!=NULL)?l1:l2;
        return head->next;
    }
};

22.*合并K个升序链表

解法1：顺序合并

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {   //顺序合并：k 个链表转化为两两合并的链表（迭代）
private:
    ListNode* mergeTwoLists(ListNode* list1,ListNode* list2){
        if(!list1 || !list2) return (list1!=nullptr)?list1:list2;  //等价于 list1?list1:list2
        ListNode *head=new ListNode(-1);
        ListNode *tail=head;
        while(list1 && list2){
            if(list1->val < list2->val){
                 tail->next=list1;
                 list1=list1->next;
            }else{
                 tail->next=list2;
                 list2=list2->next;
            }
            tail=tail->next;
        }
        tail->next=(list1==nullptr?list2:list1);
        return head->next;
    }
public:
    ListNode* mergeKLists(vector& lists) {
        ListNode *ans=nullptr;
        for(int i=0;i

• 时间复杂度：O(n*k^2)。假设每个链表的最长长度是 n。在第一次合并后，ans 的长度为 n；第二次合并后，ans 的长度为 2×n，第 i 次合并后，ans 的长度为 i×n。第 i 次合并的时间代价是 O(n+(i−1)×n)=O(i×n)，那么总的时间代价为O(n*k^2)，故渐进时间复杂度为 O(n*k^2)。

• 空间复杂度：O(1)。没有用到与 k 和 n 规模相关的辅助空间，故渐进空间复杂度为 O(1)。

解法2：分治合并

class Solution {   //分治合并：k 个链表转化为两两合并的链表（递归）
private:
    ListNode* mergeTwoLists(ListNode* list1,ListNode* list2){
        if(!list1 || !list2) return (list1!=nullptr)?list1:list2;  //等价于 list1?list1:list2
        ListNode *head=new ListNode(-1);
        ListNode *tail=head;
        while(list1 && list2){
            if(list1->val < list2->val){
                 tail->next=list1;
                 list1=list1->next;
            }else{
                 tail->next=list2;
                 list2=list2->next;
            }
            tail=tail->next;
        }
        tail->next=(list1==nullptr?list2:list1);
        return head->next;
    }
    ListNode *merge(vector& lists,int left,int right){
        if(left==right) return lists[left];
        if(left>right) return nullptr;
        int mid=(left+right)/2;
        return mergeTwoLists(merge(lists,left,mid),merge(lists,mid+1,right));
    }
public:
    ListNode* mergeKLists(vector& lists) {
        return merge(lists,0,lists.size()-1);
    }
};

• 时间复杂度：O(kn×logk)。

• 空间复杂度：O(logk)。递归会使用到 O(log⁡k) 空间代价的栈空间。

23.对链表进行插入排序

 解法1：插入排序

class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if(head==nullptr) return head;
        ListNode* dummyhead= new ListNode(0,head);
        ListNode* lastSorted=head;  // 为链表的已排序部分的最后一个节点
        ListNode* cur=head->next;   // 为待插入的元素
        
        while(cur){
            if(lastSorted->val <= cur->val){
                lastSorted = lastSorted->next;
            }else{      // 从链表的头节点开始往后遍历链表中的节点，寻找插入 cur 的位置
                ListNode* tmp = dummyhead;  // 为插入 cur 的位置的前一个节点
                while(tmp->next->val <= cur->val){
                    tmp = tmp->next;
                }

                // 插入操作:插入tmp后，lastSorted前，但不一定紧挨着 lastSorted
                lastSorted->next = cur->next;
                cur->next = tmp->next;
                tmp->next = cur;
            }
            cur = lastSorted->next;
        }
        return dummyhead->next;
    }
};

• 时间复杂度：O(n^2)，其中 n 是链表的长度。

• 空间复杂度：O(1)。

24.*排序链表

解法1：插入排序

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if(head==nullptr) return head;
        ListNode* dummyhead= new ListNode(0,head);
        ListNode* lastSorted=head;  // 为链表的已排序部分的最后一个节点
        ListNode* cur=head->next;   // 为待插入的元素
        
        while(cur){
            if(lastSorted->val <= cur->val){
                lastSorted = lastSorted->next;
            }else{      // 从链表的头节点开始往后遍历链表中的节点，寻找插入 cur 的位置
                ListNode* tmp = dummyhead;  // 为插入 cur 的位置的前一个节点
                while(tmp->next->val <= cur->val){
                    tmp = tmp->next;
                }

                // 插入操作:插入tmp后，lastSorted前，但不一定紧挨着 lastSorted
                lastSorted->next = cur->next;
                cur->next = tmp->next;
                tmp->next = cur;
            }
            cur = lastSorted->next;
        }
        return dummyhead->next;
    }
};

解法2：自底向上归并排序

思路：时间复杂度是 O(nlog⁡n) 的排序算法包括归并排序、堆排序和快速排序（快速排序的最差时间复杂度是 O(n^2)），其中最适合链表的排序算法是归并排序。归并排序基于分治算法。考虑到递归调用的栈空间，  自顶向下   归并排序的空间复杂度是 O(log⁡n)。如果要达到 O(1) 的空间复杂度，则需要使用  自底向上  的实现方式。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {   
private:
        //21.合并两个有序链表
        ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        // head 与 tail 分别代表合并链表的头部和尾部
        ListNode *head=new ListNode(-1);
        ListNode *tail=head;
        while(list1 && list2){  //两个链表都不为空
            if(list1->val < list2->val){   //此处  <=  结果一样
                tail->next=list1;
                list1=list1->next;
            }else{
                tail->next=list2;
                list2=list2->next;
            }
            tail=tail->next;   //不能忘
        }
        //至多有一个链表没有合并完，需要将链表剩余的部分加在合并链表的后面
        tail->next = (list1!=nullptr ? list1 : list2);
        return head->next;
    }
public:
       ListNode* sortList(ListNode* head) {
           if(head==nullptr){
               return head;
           }
           //计算链表的长度
           int length=0;
           ListNode *node=head;
           while(node!=nullptr){
               length++;
               node=node->next;
           }
           ListNode *dummyHead=new ListNode(0,head);
           //合并若干个长度为 subLength 的子链表。初始长度为1，每次成倍的增加
           for(int subLength=1;subLengthnext;
               while(cur!=nullptr){
                   //找到第一个符合sublength的序列
                   ListNode *list1=cur;
                   for(int i=1;inext!=nullptr;++i){
                       cur=cur->next;
                   }
                   //找到第二个符合sublength的序列
                   ListNode *list2=cur->next;
                   cur->next=nullptr;  // 断尾巴
                   cur=list2;
                   for(int i=1;inext!=nullptr;++i){
                       cur=cur->next;
                   }
                   // 要看第二个头是不是在list最后， 如果不是则要记录第三个头
                   ListNode *next=nullptr;
                   if(cur!=nullptr){
                       next=cur->next;
                       cur->next=nullptr;
                   }
                   ListNode *merged=mergeTwoLists(list1,list2);
                   pre->next=merged; //pre指向新归并出来的list
                   while(pre->next!=nullptr){
                       pre=pre->next;
                   }
                   cur=next; //将cur更新到第三个头，进行循环
               }
           }
           return dummyHead->next;
       }
};

• 时间复杂度：O(nlog⁡n)，其中 n 是链表的长度。

• 空间复杂度：O(1)。

解法3：自顶向下归并排序

思路：（1）找到链表的中点，以中点为分界，将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法，快指针每次移动 2 步，慢指针每次移动 1 步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中点。（2）对两个子链表分别排序。（3）将两个排序后的子链表合并，得到完整的排序后的链表。

class Solution {   
private:
        //21.合并两个有序链表
        ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        // head 与 tail 分别代表合并链表的头部和尾部
        ListNode *head=new ListNode(-1);
        ListNode *tail=head;
        while(list1 && list2){  //两个链表都不为空
            if(list1->val < list2->val){   //此处  <=  结果一样
                tail->next=list1;
                list1=list1->next;
            }else{
                tail->next=list2;
                list2=list2->next;
            }
            tail=tail->next;   //不能忘
        }
        //至多有一个链表没有合并完，需要将链表剩余的部分加在合并链表的后面
        tail->next = (list1!=nullptr ? list1 : list2);
        return head->next;
    }
public:
       ListNode* sortList(ListNode* head) {
           if (head==nullptr || head->next==nullptr)  return head;
           ListNode *slow=head,*fast=head,*pre=nullptr;
           while (fast!=nullptr && fast->next!=nullptr) {
               pre=slow;
               slow=slow->next;
               fast=fast->next->next;
           }
           //此时slow指针指向中间结点，用pre指针把链表从中间断开,分为[head,pre],[slow,fast]两段
           pre->next=nullptr;
           return mergeTwoLists(sortList(head), sortList(slow));
    }
};

• 时间复杂度：O(nlog⁡n)，其中 n 是链表的长度。

• 空间复杂度：O(logn)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。

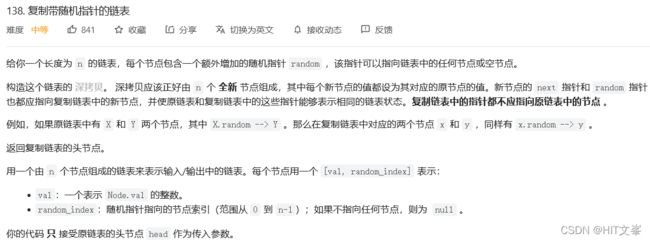
25.复制带随机指针的链表

 

 解法1：递归+哈希

思路：如果是普通链表，我们可以直接按照遍历的顺序创建链表节点。而本题中因为随机指针的存在，当我们拷贝节点时，「当前节点的随机指针指向的节点」可能还没创建。让每个节点的拷贝操作相互独立。对于当前节点，我们首先要进行拷贝，然后我们进行「当前节点的后继节点」和「当前节点的随机指针指向的节点」拷贝，拷贝完成后将创建的新节点的指针返回，即可完成当前节点的两指针的赋值。具体地，我们用哈希表记录每一个节点对应新节点的创建情况。如果这两个节点中的任何一个节点的新节点没有被创建，我们都立刻递归地进行创建。如果已经拷贝过，我们可以直接从哈希表中取出拷贝后的节点的指针并返回即可。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;   
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};*/
class Solution {
public:
    unordered_map hashtable;
    Node* copyRandomList(Node* head) {
        if(!head) return NULL;
        //unordered_map hashtable; 放在此处为错误
        while(!hashtable.count(head)){
            Node* headNew=new Node(head->val);
            hashtable[head]=headNew;
            headNew->next=copyRandomList(head->next);
            headNew->random=copyRandomList(head->random);
        }
        return hashtable[head];//返回新链表的头节点
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。对于每个节点，我们至多访问其「后继节点」和「随机指针指向的节点」各一次，均摊每个点至多被访问两次。

• 空间复杂度：O(n)，其中 n 是链表的长度。为哈希表的空间开销。

26.#复杂链表的复制

 

解法1：递归+哈希

class Solution {
public:
    unordered_map hashtable;
    Node* copyRandomList(Node* head) {
        if(!head) return NULL;
        //unordered_map hashtable; 放在此处为错误
        while(!hashtable.count(head)){
            Node* headNew=new Node(head->val);
            hashtable[head]=headNew;
            headNew->next=copyRandomList(head->next);
            headNew->random=copyRandomList(head->random);
        }
        return hashtable[head];//返回新链表的头节点
    }
};

• 时间复杂度：O(n)，其中 n 是链表的长度。对于每个节点，我们至多访问其「后继节点」和「随机指针指向的节点」各一次，均摊每个点至多被访问两次。

• 空间复杂度：O(n)，其中 n 是链表的长度。为哈希表的空间开销。

题型三：哈希表

0.哈希表的基础知识

（1）当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。但是哈希法也是牺牲了空间换取了时间，因为我们要使用额外的数组，set或者是map来存放数据，才能实现快速的查找。如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法！

（2）常见的三种哈希结构：

• 数组：数组就是简单的哈希表，但是数组的大小不能无限的开辟。如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。
• set（集合）
• map（映射）

  集合/映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
  std::set	红黑树	有序	否	否	O(logn)	O(logn)
  std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
  std::unordered_set	哈希表	无序	否	否	O(1)	O(1)
  std::map	红黑树	key有序	否	否	O(logn)	O(logn)
  std::multimap	红黑树	key有序	是	否	O(logn)	O(logn)
  std::unordered_map	哈希表	key无序	否	否	O(1)	O(1)

（3）特点 ：红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的，如果需要集合是有序的，那么就用set，如果要求不仅有序还要有重复数据的话，那么就用multiset。

1.有效的字母异位词

 解法1：哈希

思路：t 是 s 的异位词等价于「两个字符串中字符出现的种类和次数均相等」

因为字符a到字符z的ASCII是26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。在遍历 字符串s 的时候，只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可，并不需要记住字符a的ASCII，只要求出一个相对数值就可以。 这样就将字符串s中字符出现的次数，统计出来了。

class Solution {
public:
    bool isAnagram(string s, string t) {        
       if(s.length()!=t.length()){
           return false;
       }

       vectortable(26,0);   //长度为26的数组作为哈希表
       for(auto &ch:s){          //先遍历记录字符串s中字符出现的频次
           table[ch-'a']++;
       }

       for(auto &ch:t){          //再遍历字符串t，减去table中出现的频次
           table[ch-'a']--;
           if(table[ch-'a']<0){  //注意此处 <
               return false;
           }
       }
       return true;
    }
};

• 时间复杂度：O(n)，其中 n 为 s 的长度。

• 空间复杂度：O(1)，只需字符集的大小26。

 解法2：排序

思路：t 是 s 的异位词等价于「两个字符串排序后相等」。

class Solution {
public:
    bool isAnagram(string s, string t) {
       if(s.length()!=t.length()){
           return false;
       }

       //两字符串排序后相等
       sort(s.begin(),s.end());
       sort(t.begin(),t.end());
       return s==t;
    }
};

• 时间复杂度：O(nlogn)，其中 n 为 s 的长度。

  排序的时间复杂度为 O(nlog⁡n)，比较两个字符串是否相等时间复杂度为 O(n)，因此总体时间复杂度为 O(nlog⁡n+n)=O(nlog⁡n)。

• 空间复杂度：O(logn)，排序需要 O(log⁡n) 的空间复杂度。

2.字母异位词分组

 解法1：哈希+排序

class Solution {
public:
    vector> groupAnagrams(vector& strs) {
         unordered_map> mp;     //将排序后的字符串作为哈希表的键
         for(string &str:strs) {        
             string key =str;
             sort(key.begin(),key.end());
             mp[key].emplace_back(str);    //更高效的插入方法：emplace_back.类似于insert和push
         }    

         vector> ans;
         for(auto it=mp.begin();it!=mp.end();++it){
             ans.emplace_back(it->second);
         }
         return ans;
    }
};

• 时间复杂度：O(k*nlogn)，其中 k 是 strs 中的字符串的数量，n 是 strs 中的字符串的的最大长度。需要遍历 n 个字符串，对于每个字符串，需要 O(nlog⁡n) 的时间进行排序以及 O(1) 的时间更新哈希表，因此总时间复杂度是 O(k*nlogn)。

• 空间复杂度：O(k*n)，其中 k 是 strs 中的字符串的数量，n 是 strs 中的字符串的的最大长度。需要用哈希表存储全部字符串。

3.*找到字符串中所有字母异位词

 解法1：哈希+滑动窗口

class Solution {
public:
    vector findAnagrams(string s, string p) {
        int sLen=s.length(),pLen=p.length();
        if(sLen();
        vector ans;
        //使用数组来存储字符串 p 和滑动窗口中每种字母的数量。
        vector sCount(26);
        vector pCount(26);
        for(int i=0;i

• 时间复杂度：O(m+(n−m)×Σ)，其中 n 为字符串 s 的长度，m 为字符串 p 的长度，Σ 为所有可能的字符数。我们需要 O(m) 来统计字符串 p 中每种字母的数量；需要 O(m) 来初始化滑动窗口；需要判断 n-m+1 个滑动窗口中每种字母的数量是否与字符串 p 中每种字母的数量相同，每次判断需要 O(Σ) 。因为 s 和 p 仅包含小写字母，所以 Σ=26。

• 空间复杂度：O(Σ)，用于存储字符串 p 和滑动窗口中每种字母的数量。

4.赎金信

 

 解法1：哈希

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        if(ransomNote.length()>magazine.length()){
            return false;
        }

        vector visited(26,0); //可以不赋初值，但不可以不定义长度
        for(auto &ch:magazine){
            visited[ch-'a']++;
        }
        for(auto &ch:ransomNote){
            visited[ch-'a']--;
            if(visited[ch-'a']<0){
                return false;
            }
        }
      return true;
    }
};

• 时间复杂度：O(m+n)，其中 m 是字符串 ransomNote 的长度，n 是字符串 magazine 的长度，我们只需要遍历两个字符一次即可。

• 空间复杂度：O(∣S∣)，S 是字符集，这道题中 S 为全部小写英语字母，因此 ∣S∣=26。

 5.两个数组的交集

 解法1：哈希

class Solution {
public:
    vector intersection(vector& nums1, vector& nums2) {
        unordered_set ans;  //哈希表存放结果
        unordered_set nums_set(nums1.begin(),nums1.end());//数组1中的元素放入哈希表中
        for(int num:nums2){
            if(nums_set.find(num)!=nums_set.end()){
                ans.emplace(num);   //ans.insert(num);也可。就是push_back、push和emplace_back不行
            }
        }
        return vector(ans.begin(),ans.end());
    }
};

• 时间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。使用两个集合分别存储两个数组中的元素需要 O(m+n) 的时间。

• 空间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。空间复杂度主要取决于两个集合。

 解法2：排序+双指针

思路：首先对两个数组进行排序，然后使用两个指针遍历两个数组。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，且该数字不等于上一次加入答案数组的元素 ，将该数字添加到答案并更新 答案数组的元素，同时将两个指针都右移一位。

class Solution {
public:
    vector intersection(vector& nums1, vector& nums2) {
       sort(nums1.begin(),nums1.end());
       sort(nums2.begin(),nums2.end());
       int length1=nums1.size(),length2=nums2.size();
       int index1=0,index2=0;
       vector ans;

       while(index1

• 时间复杂度：O(mlogm+nlogn)，其中 m 和 n 分别是两个数组的长度。对两个数组排序的时间复杂度分别是 O(mlog⁡m) 和 O(nlog⁡n)，双指针寻找交集元素的时间复杂度是 O(m+n)，因此总时间复杂度是 O(mlog⁡m+nlog⁡n)。

• 空间复杂度：O(logm+logn)，其中 m 和 n 分别是两个数组的长度。空间复杂度主要取决于排序使用的额外空间。

 6.两个数组的交集II

 解法1：哈希

class Solution {
public:
    vector intersect(vector& nums1, vector& nums2) {
      if(nums1.size()>nums2.size()){
          return intersect(nums2,nums1);   //先遍历较小的数组，可以减少时间复杂度
      }
      unordered_map m;
      for(int num:nums1){
          ++m[num];
      }

      vector ans;
      for(int num:nums2){
          //如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。
          if(m.count(num)){
              ans.push_back(num);
              --m[num];

              if(m[num]==0){ //重要
                  m.erase(num);
              }              
          }
      }
      return ans;
    }
};

• 时间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。需要遍历两个数组并对哈希表进行操作，哈希表操作的时间复杂度是 O(1)，因此总时间复杂度与两个数组的长度和呈线性关系。

• 空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个数组的长度。对较短的数组进行哈希表的操作，哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组 ans，其长度为较短的数组的长度。

 解法2：排序+双指针

class Solution {
public:
    vector intersect(vector& nums1, vector& nums2) {
        sort(nums1.begin(),nums1.end());
        sort(nums2.begin(),nums2.end());
        int length1=nums1.size(),length2=nums2.size();
        int index1=0,index2=0;
        vector ans;
 
        while(index1

• 时间复杂度：O(mlogm+nlogn)，其中 m 和 n 分别是两个数组的长度。对两个数组排序的时间复杂度分别是 O(mlog⁡m) 和 O(nlog⁡n)，双指针寻找交集元素的时间复杂度是 O(m+n)，因此总时间复杂度是 O(mlog⁡m+nlog⁡n)。

• 空间复杂度：O(1)

7.快乐数

 解法1：哈希

思路：无限循环说明求和的过程中，sum会重复出现。使用哈希法，来判断这个sum是否重复出现，如果重复了就是return false， 否则一直找到sum为1为止。

class Solution {
private:
    int getSum(int n){
          int sum=0;
          while(n>0){
              sum+=(n%10)*(n%10);
              n/=10;
          }
          return sum;
      }
public:
    bool isHappy(int n) {
        unordered_set unset;
        while(n!=1 && !unset.count(n)){
           unset.insert(n);
           n=getSum(n);
         }
        return n==1;
    }
};

只计算 getSum(n) 函数的时间复杂度 ：

• 时间复杂度：O(logn)

• 空间复杂度：O(logn)

解法2：快慢指针

思路：这个问题就可以转换为检测一个链表是否有环。快指针走两步，慢指针走一步。
           如果 n 是一个快乐数，即没有循环，那么快指针最终会比慢指针先到达数字 1。
           如果 n 不是一个快乐的数字，那么最终快指针和慢指针将在同一个数字上相遇。

class Solution {
private:
    int getSum(int n){
          int sum=0;
          while(n){
              sum+=(n%10)*(n%10);
              n/=10;
          }
          return sum;
      }
public:
    bool isHappy(int n) {
      //快慢指针针对循环很高效
      int slow=n,fast=getSum(n);   //注意快慢指针的起始位置不同（起始位置相同可以用do-while语句）
      while(fast!=1 && slow!=fast){
          slow=getSum(slow);
          fast=getSum(getSum(fast));
      }
      return fast==1;
      
    }
};

• 时间复杂度：O(logn)

• 空间复杂度：O(1)，我们不需要哈希集来检测循环，指针需要常数的额外空间。

8.*和为K的子数组

 解法1：枚举

class Solution {
public:
    int subarraySum(vector& nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.size(); ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
};

• 时间复杂度：O(n^2)，其中 n 为数组的长度。

• 空间复杂度：O(1)。

解法2：哈希+前缀和

class Solution {
public:
    int subarraySum(vector& nums, int k) {
        //以和为键，出现次数为对应的值，记录 pre[i] 出现的次数
        unordered_map umap;
        umap[0]=1;  //初始化：和为0的个数有一次
        int count=0,pre=0;
        for(auto &x:nums){
            //pre[i] 为 [0..i] 里所有数的和
            //由于pre[i] 的计算只与前一项的答案有关，因此我们可以不用建立 pre 数组，直接用 pre 变量来记录 pre[i−1] 的答案即可
            pre+=x;
            //[j..i] 这个子数组和为 k 转化为 pre[j−1]==pre[i]−k
            if(umap.find(pre-k) != umap.end()){
                count+=umap[pre-k];
            }
            umap[pre] ++;  //将 pre 放入哈希表中
        }
        return count;
    }
};

• 时间复杂度：O(n)，其中 n 为数组的长度。我们遍历数组的时间复杂度为 O(n)，中间利用哈希表查询删除的复杂度均为 O(1)，因此总时间复杂度为 O(n)。

• 空间复杂度：O(n)，其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值，因此需要 O(n) 的空间复杂度。

9. *两数之和

 解法1：哈希

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        unordered_map hashtable;
        for (int i = 0; i < nums.size(); ++i) {
            //遍历  auto默认为迭代器 unordered_map::iterator
            auto it = hashtable.find(target - nums[i]);  //寻找（target-nums[i]）是否在map中            
            if (it != hashtable.end()) {
                return {it->second, i};    //map<数值，下标>
            }
            hashtable[nums[i]] = i;  //等价于hashtable.insert(pair(nums[i],i)); 
        }
        return {};
    }
};

• 时间复杂度：O(n)，其中 n 是数组中的元素数量。对于每一个元素 x，我们可以 O(1) 地寻找 target - x。

• 空间复杂度：O(n)，其中 n 是数组中的元素数量。主要为哈希表的开销。

 解法2：暴力

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        int n = nums.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return {i, j};
                }
            }
        }
        return {};
    }
};

• 时间复杂度：O(n^2)，其中 n 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。

• 空间复杂度：O(1)

10.#和为s的两个数字

解法1：哈希

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        unordered_set hashtable;
        for(int i=0;i

解法2：前后指针

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<=right){
            if(nums[left]+nums[right]>target){
                right--;
            }else if(nums[left]+nums[right]

11.#和为s的连续正数序列

 解法1：滑动窗口

class Solution {
public:
    vector> findContinuousSequence(int target) {
        vector> ans;
        vector vec;        
        for(int l=1,r=2;ltarget){
                l++;
            }else{
                r++;
            }
        }
        return ans;
    }
};

• 时间复杂度：由于两个指针移动均单调不减，且最多移动 [target/2]次，即方法一提到的枚举的上界，所以时间复杂度为 O(target) 。

• 空间复杂度：O(1) ，除了答案数组只需要常数的空间存放若干变量。

12.三数之和

 解法1：排序+双指针

思路： 有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。a = nums[i]， b = nums[left]， c = nums[right]。

如果nums[i] + nums[left] + nums[right] > 0 就说明此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。

本题并不适合用哈希：两层for循环就可以确定 a 和b 的数值了，可以使用哈希法来确定 0-(a+b) 是否在数组里出现过，但题目中说的不可以包含重复的三元组。把符合条件的三元组放进vector中，然后再去重，这样是非常费时的，很容易超时。

class Solution {
public:
    vector> threeSum(vector& nums) {
      sort(nums.begin(),nums.end());    //排序+双指针
      vector> ans;
      for(int i=0;i0)  return ans;
          //去重：保证和上一次枚举的数不相同
          if(i>0&&nums[i]==nums[i-1])  continue;  //重要

          int left=i+1,right=nums.size()-1;
          while(left0){
                  right--;
              }else if(nums[i]+nums[left]+nums[right]<0){
                  left++;
              }else{
                  ans.push_back({nums[i],nums[left],nums[right]});
                  //去重 : 应该放在找到一个三元组之后（防止忽略情况：0，0，0）
                  while(left

• 时间复杂度：O(n^2)，其中 n 是数组 nums 的长度。

• 空间复杂度：O(n)，使用了一个额外的数组存储了 nums 的副本并进行排序，空间复杂度为 O(n)。

13.四数之和

 解法1：排序+双指针

class Solution {
public:
    vector> fourSum(vector& nums, int target) {    
        sort(nums.begin(), nums.end());  
        vector> ans;
        if (nums.size() < 4) {
            return ans;
        }
        //使用两重循环分别枚举前两个数，然后在两重循环枚举到的数之后使用双指针枚举剩下的两个数
        for (int i = 0; i < nums.size(); i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;  //去重
            for (int j = i + 1; j < nums.size(); j++) {
                if (j > i + 1 && nums[j] == nums[j - 1])  continue;  //正确去重
                int left=j+1,right=nums.size()-1; 
                while (left < right) {
                    //nums[i]+nums[j]+nums[left]+nums[right] < target  容易溢出
                    if(nums[i]+nums[j]target-nums[left]-nums[right]){
                        right--;
                    }else{
                        ans.push_back({nums[i],nums[j],nums[left],nums[right]});
                        // 去重逻辑应该放在找到一个四元组之后
                        while (left < right && nums[left] == nums[left + 1]) {
                            left++;
                        }
                        left++;
                        while (left < right && nums[right] == nums[right - 1]) {
                            right--;
                        }
                        right--;
                    }
                }
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n^3)，其中 n 是数组 nums 的长度。

  排序的时间复杂度是 O(nlog⁡n)，枚举四元组的时间复杂度是 O(n^3)，因此总时间复杂度为 O(n^3+nlog n)=O(n^3)。

• 空间复杂度：O(n)，使用了一个额外的数组存储了 nums 的副本并进行排序，空间复杂度为 O(n)。

14.四数相加II

 解法1：哈希

思路：这道题目是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况。

对于 A 和 B，我们使用二重循环对它们进行遍历，得到所有 A[i]+B[j] 的值并存入哈希映射中。对于哈希映射中的每个键值对，每个键表示一种 A[i]+B[j]，对应的值为 A[i]+B[j] 出现的次数。

在遍历C和D数组，找到如果 0-(c+d) 在map中出现过的话，就把map中key对应的value也就是出现次数统计出来。

class Solution {
public:
    int fourSumCount(vector& nums1, vector& nums2, vector& nums3, vector& nums4) {
       //4个数组分两组+哈希表
       unordered_map countAB;
       for(int u:nums1){
           for(int v:nums2){
               ++countAB[u+v];
           }
       }

       int ans=0;
       for(int u:nums3){
           for(int v:nums4){    
               if(countAB.count(-u-v)){
                   ans+=countAB[-u-v];     //一定要是[]
               }
           }
       }
       return ans;
    }
};

• 时间复杂度：O(n^2)，我们使用了两次二重循环，时间复杂度均为 O(n^2)。在循环中对哈希映射进行的修改以及查询操作的期望时间复杂度均为 O(1)，因此总时间复杂度为 O(n^2)。

• 空间复杂度：O(n^2)，即为哈希映射需要使用的空间。在最坏的情况下，A[i]+B[j] 的值均不相同，因此值的个数为 n^2，也就需要 O(n^2) 的空间。

15.独一无二的出现次数

 

 解法1：哈希

思路：首先使用哈希表记录每个数字的出现次数；随后再利用新的哈希表，统计不同的出现次数的数目。如果不同的出现次数的数目 = 不同数字的数目，则返回 true，否则返回 false。

class Solution {
public:
    bool uniqueOccurrences(vector& arr) {
        //map统计：不同数字的数目
        unordered_map umap;
        for(const auto&x: arr){
            umap[x]++;
        }
        //set可以把相同数目合并，统计每个数字的出现次数的数目
        unordered_set uset;
        for(const auto&x: umap){
            uset.insert(x.second);
        }
        return uset.size()==umap.size();
    }
};

• 时间复杂度：O(n)，其中 n 为数组的长度。遍历原始数组需要 O(n) 时间，而遍历中间过程产生的哈希表又需要 O(n) 的时间。

• 空间复杂度：O(n)，即为哈希需要使用的空间。

16.同构字符串

解法1：哈希 （双射）

class Solution {
public:
    bool isIsomorphic(string s, string t) {
        unordered_map s2t;//以 s 中字符为键，映射至 t 的字符为值
        unordered_map t2s;//以 t 中字符为键，映射至 s 的字符为值
        for (int i=0,j=0; i < s.size(); ++i,++j) {
            if ((s2t.count(s[i]) && s2t[s[i]] != t[j]) || (t2s.count(t[j]) && t2s[t[j]] != s[i])) {
                return false;
            }
            s2t[s[i]] = t[j];
            t2s[t[j]] = s[i];
        }
        return true;
    }
};

class Solution {
public:
    bool isIsomorphic(string s, string t) {
        unordered_map s2t;
        unordered_map t2s;
        for(int i=0,j=0;i

• 时间复杂度：O(n)，其中 n 为字符串的长度。我们只需同时遍历一遍字符串 s 和 t 即可。

• 空间复杂度：O(∣Σ∣)，其中 Σ 是字符串的字符集。哈希表存储字符的空间取决于字符串的字符集大小，最坏情况下每个字符均不相同，需要 O(∣Σ∣) 的空间。

17.单词规律

解法1：哈希（双射）

class Solution {   //双射问题
public:
    bool wordPattern(string pattern, string str) {
        unordered_map str2ch;
        unordered_map ch2str;
        int m = str.length();
        int i = 0;
        for (auto ch : pattern) {
            if (i >= m) {
                return false;
            }
            //截取字符串中的单词
            int j = i;
            while (j < m && str[j] != ' ')  j++;
            const string tmp = str.substr(i, j - i);

            if (str2ch.count(tmp) && str2ch[tmp] != ch)  {return false;}
            if (ch2str.count(ch)  && ch2str[ch] != tmp)  {return false;}
            str2ch[tmp] = ch;
            ch2str[ch] = tmp;
            i = j + 1;
        }
        return i >= m;
    }
};

• 时间复杂度：O(m+n)，其中 m 为 pattern 的长度，n 为 str 的长度。插入和查询哈希表的均摊时间复杂度均为 O(m+n)。每一个字符至多只被遍历一次。

• 空间复杂度：O(m+n)，最坏情况下，我们需要存储 pattern 中的每一个字符和 str 中的每一个字符串。

18.*无重复字符的最长子串

 解法1：哈希+滑动窗口

class Solution {   //注意子串 与 子序列的区别
public:
    int lengthOfLongestSubstring(string s) {
        //哈希表：记录每个字符是否重复出现过
        unordered_map umap;
        int start=0,ans=0;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是字符串的长度。

• 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣ 表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0,128) 内的字符，即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有 ∣Σ∣ 个，因此空间复杂度为 O(∣Σ∣)。

19. #最长不含重复字符的子字符串

解法1：哈希+滑动窗口

class Solution {   //注意子串 与 子序列的区别
public:
    int lengthOfLongestSubstring(string s) {
        //哈希表：记录每个字符是否重复出现过
        unordered_map umap;
        int start=0,ans=0;
        for(int i=0;i

20.*最长连续序列

 解法1：哈希

思路：如果已知有一个 x,x+1,x+2,⋯ ,x+y 的连续序列，而我们却重新从 x+1，x+2 或者是 x+y 处开始尝试匹配，那么得到的结果肯定不会优于枚举 x 为起点的答案，因此我们在外层循环的时候碰到这种情况跳过即可。因此我们要枚举的数 x 一定是在数组中不存在前驱数 x−1 的，所以我们每次在哈希表中检查是否存在 x−1 即能判断是否需要跳过了。

class Solution {
public:
    int longestConsecutive(vector& nums) {
        // 使用哈希表 去重
        unordered_set uset;
        for(const int&num:nums){
            uset.insert(num);
        }

        int ans=0;
        for(const int&num:uset){
            if(!uset.count(num-1)){  //哈希表中不存在当前数的前一个数，才可以继续遍历，否则跳过，防止重复遍历
                int curNum=num;
                int curLong=1;
                while(uset.count(curNum+1)){  //利用哈希表遍历数组中是否存在这个数
                    curNum  +=1;
                    curLong +=1;
                }
                ans=max(ans,curLong);
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 为数组的长度。外层循环需要 O(n) 的时间复杂度，只有当一个数是连续序列的第一个数的情况下才会进入内层循环，然后在内层循环中匹配连续序列中的数，因此数组中的每个数只会进入内层循环一次。

• 空间复杂度：O(n)，哈希表存储数组中所有的数需要 O(n) 的空间。

21.#第一个只出现一次的字符

 解法1：哈希

思路：在第一次遍历时，我们使用哈希映射统计出字符串中每个字符出现的次数。在第二次遍历时，我们只要遍历到了一个只出现一次的字符，那么就返回该字符，否则在遍历结束后返回空格。

class Solution {
public:
    char firstUniqChar(string s) {
        unordered_map hashtable;
        for(char ch:s){
            ++hashtable[ch];
        }
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。我们需要进行两次遍历。

• 空间复杂度：O(∣Σ∣)，其中 Σ 是字符集，在本题中 s 只包含小写字母，因此 ∣Σ∣≤26。我们需要 O(∣Σ∣) 的空间存储哈希映射。

22.*LRU缓存

 解法1：哈希+双向链表

 思路：（1）一旦出现key和value，就要想到哈希表。（2）对数据的访问为get 和put 就需要随机的访问数据，需要把数据插到头部或者尾部。（3）链表可以快速移动节点位置。（4）哈希表可以实现时间复杂度度为O(1)的快速访问，哈希表的  值包括 用户输入值 和 链表的位置信息（用双向链表DListNode*），就可以在O(1)时间里访问链表。（5）链表记录了访问的时间信息，链表元素必须存储  键 ，通过键找到哈希表。（6）链表 头部 为最近访问的节点。

 a) 双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。b) 一个节点移到双向链表的头部，可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作，都可以在 O(1) 时间内完成。 c) 在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

//手写一个双向链表的数据结构
struct DListNode{
    int key,value;
    DListNode *pre;
    DListNode *next;
    DListNode():key(0),value(0),pre(nullptr),next(nullptr){}
    DListNode(int m_key,int m_value):key(m_key),value(m_value),pre(nullptr),next(nullptr){}
};   //定义结构体记得 加 分号

class LRUCache {     //哈希表 + 双向链表
private:
    //删除
    void removeNode(DListNode *node){
        node->pre->next=node->next;
        node->next->pre=node->pre;
    }
    //插入：新链表插入到链表头部
    //双向链表：插入一个节点有4个指向
    void addToHead(DListNode *node){
        //节点 node 指向前后
        node->pre=dummyHead;
        node->next=dummyHead->next;
        //前后指向 节点node
        dummyHead->next->pre=node;
        dummyHead->next=node;
    }

    void moveToHead(DListNode *node){
        removeNode(node);
        addToHead(node);
    }
    DListNode* removeTail(){
        DListNode *node=dummyTail->pre;
        removeNode(node);
        return node;
    }  

    int size,capacity;
    DListNode *dummyHead,*dummyTail;
    unordered_map cache;
public:
    //1、以 正整数 作为容量 m_capacity 初始化 LRU 缓存
    LRUCache(int m_capacity):capacity(m_capacity),size(0) {
        // 使用伪头部和伪尾部节点
        dummyHead=new DListNode();
        dummyTail=new DListNode();
        dummyHead->next=dummyTail;
        dummyTail->pre=dummyHead;
    }
    
    //2、如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
    int get(int key) {
        if(!cache.count(key)){ //key不存在
            return -1;
        }
        //key存在：先通过哈希表定位，再移到头部（使用过，就及时的更新）
        DListNode *node=cache[key];
        //moveToHead(node);
        removeNode(node);
        addToHead(node);

        return node->value;
    }
    
    //3、如果关键字 key 已经存在，则 变更 其数据值 value ；
    //   如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
    void put(int key, int value) {
        if(!cache.count(key)){
            //key 不存在
            DListNode *node=new DListNode(key,value); //创建一个新的节点
            cache[key]=node;                          //添加进哈希表
            addToHead(node);                          //添加至双向链表的头部
            ++size;
            if(size>capacity){
                DListNode *removed=removeTail();  //删除双向链表的尾部节点
                cache.erase(removed->key);        // 删除哈希表中对应的项
                delete removed;                   // 防止内存泄漏
                --size;
            }
        }else{
            //key 存在：先通过哈希表定位，再修改 value，并移到头部
            DListNode *node=cache[key];
            node->value=value;
            moveToHead(node);
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

• 时间复杂度：O(1)，对于 put 和 get 都是 O(1)。

• 空间复杂度：O(capacity)，因为哈希表和双向链表最多存储 capacity+1 个元素。

23.*找到所有数组中消失的数字

 解法1：哈希

class Solution {
public:
    vector findDisappearedNumbers(vector& nums) {
        //用一个长度为 n 的原数组nums来代替哈希表
        int n=nums.size();
        for(auto &num:nums){
            //得到num值对应的下标，当我们遍历到某个位置时，其中的数可能已经被增加过，因此需要对 n 取模来还原出它本来的值。
            int x=(num-1)%n;   
            //num-1下标位置的数+n放入nums数组中。由于 nums 中所有数均在 [1,n] 中，增加以后，这些数必然大于 n
            nums[x]+=n;
        }
        //最后我们遍历 nums，若 nums[i] 未大于 n，就说明没有遇到过数 i+1。这样我们就找到了缺失的数字
        vector ans;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。

• 空间复杂度：O(1)，返回值不计入空间复杂度。

题型四：字符串

1.反转字符串

 解法1：前后指针

class Solution {
public:
    void reverseString(vector& s) {
      for(int left=0,right=s.size()-1;left

• 时间复杂度：O(n)，其中 n 为字符数组的长度。一共执行了 n/2 次的交换。

• 空间复杂度：O(1)，只使用了常数空间来存放若干变量。

 2.反转字符串II

解法1：模拟

class Solution {
public:
    //反转每个下标从 2k 的倍数开始的，长度为 k 的子串。若该子串长度不足 k，则反转整个子串。
    string reverseStr(string s, int k) {
        int n=s.length();
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。

• 空间复杂度：O(1)

 3.#替换空格

解法1：模拟

class Solution {
public:
    string replaceSpace(string s) {
         string array;   //存储替换结果
         for(auto &c:s){
             if(c==' '){
                 array += "%20";
             }else{
                 array += c; //不带引号
             }
         }
         return array;
    }
};

• 时间复杂度：O(n)，遍历字符串 s 一遍。

• 空间复杂度：O(n)，额外创建字符数组，长度为 s 的长度的 3 倍。

解法2：双指针

 思路：很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。两个好处：1、不用申请新数组。2、从后向前填充元素，避免了从前先后每次添加元素都要将添加元素之后的所有元素向后移动，降低了时间复杂度。

class Solution {
public:
    string replaceSpace(string s) {
        int count = 0; // 统计空格的个数
        int sOldSize = s.size();
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == ' ') {
                count++;
            }
        }
        
        // 扩充字符串s的大小，也就是每个空格替换成"%20"之后的大小
        s.resize(s.size() + count * 2);
        int sNewSize = s.size();
        // 从后先前将空格替换为"%20"
        for (int i = sNewSize - 1, j = sOldSize - 1; j < i; i--, j--) {
            if (s[j] != ' ') {
                s[i] = s[j];
            } else {
                s[i] = '0';
                s[i - 1] = '2';
                s[i - 2] = '%';
                i -= 2;
            }
        }
        return s;
    }
};

• 时间复杂度：O(n)，遍历字符串 s 一遍。

• 空间复杂度：O(1)

 4.翻转字符串里的单词

 解法1：快慢指针

思路：先整体旋转再局部旋转。1、移除多余空格   2、将整个字符串反转  3、将每个单词反转

class Solution {
private:
    // 移除冗余空格：使用快慢指针法O(n)的算法
    void removeExtraSpaces(string& s) {
        int slow=0,fast=0;
        // 去掉(翻转前)字符串前面的空格
        while(fast0 && s[fast-1]==s[fast]  && s[fast]==' '){
                continue;
            }else{
                s[slow++]=s[fast];
            }
        }        
        // 去掉字符串末尾的空格
        if(slow-1>0 && s[slow-1]==' '){
            s.resize(slow-1);
        }else{
            s.resize(slow);    //重新设置字符串大小
        }
    }
public:
    string reverseWords(string s) {
        removeExtraSpaces(s);
        reverse(s.begin(),s.end());
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 为输入字符串的长度。

• 空间复杂度：O(1)，不要使用辅助空间。

5.#翻转单词顺序

 解法1:快慢指针

class Solution {
private:
    // 移除冗余空格：使用快慢指针法O(n)的算法
    void removeExtraSpaces(string& s) {
        int slow=0,fast=0;
        // 去掉(翻转前)字符串前面的空格
        while(fast0 && s[fast-1]==s[fast]  && s[fast]==' '){
                continue;
            }else{
                s[slow++]=s[fast];
            }
        }        
        // 去掉字符串末尾的空格
        if(slow-1>0 && s[slow-1]==' '){
            s.resize(slow-1);
        }else{
            s.resize(slow);    //重新设置字符串大小
        }
    }
public:
    string reverseWords(string s) {
        removeExtraSpaces(s);
        reverse(s.begin(),s.end());
        for(int i=0;i

6.#左旋转字符串

 解法1：局部反转+整体反转

思路：1、反转区间为前n的子串   2、反转区间为n到末尾的子串   3、整体反转字符串

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        reverse(s.begin(),s.begin()+n);
        reverse(s.begin()+n,s.end());
        reverse(s.begin(),s.end());
        return s;
    }
};

• 时间复杂度：O(n)，其中 n 为字符串 s 的长度。

• 空间复杂度：O(1)，不要使用辅助空间。

 使用substr 的时间复杂度也是O(n),空间复杂度是O(n) 因为申请了额外空间

7. 实现 strStr()

KMP算法的知识点

 （1）KMP主要应用在字符串匹配上。KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配。

（2） next数组就是一个前缀表（prefix table）。前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

（3）前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

         后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

         需要找到KMP最长相等前后缀

 （4）next数组既可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。仅仅是KMP的实现方式的不同。

 解法1：KMP算法（前缀表统一减一）

class Solution {
public:
    int strStr(string haystack, string needle) {
        if (needle.length() == 0) {
            return 0;
        }
        vector next(needle.length(),-1); //必须初始化为-1，否则超时
        // 1、求 needle 部分的前缀表，我们需要保留这部分的前缀函数值。
        // 注意i从1开始，j从-1开始。i指向后缀末尾位置，j指向前缀末尾位置。
        for(int i = 1,j=-1; i < needle.length(); i++) { 
            while (j >= 0 && needle[i] != needle[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回退
            }

            if (needle[i] == needle[j + 1]) { // 找到相同的前后缀
                j++;     // 同时向后移动i 和j 
            }
            next[i] = j; // next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
        }       
      
        // 2、求 haystack 部分的前缀函数，我们无需保留这部分的前缀函数值，只需要用一个变量记录上一个位置的前缀函数值即可。
        // 注意i就从0开始，j从-1开始（因为next数组里记录的起始位置为-1）。
        // i指向文本串起始位置，j 指向模式串起始位置。
        for (int i = 0,j = -1; i < haystack.length(); i++) { 
            while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // 同时向后移动i 和j，i的增加在for循环里
            }

            // j指向了模式串needle的末尾，说明文本串haystack里出现了模式串needle
            if (j == (needle.length() - 1) ) { 
                // 返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。
                return (i - needle.length() + 1);
            }
        }
        return -1;
    }
};

• 时间复杂度：O(m+n)，我们至多需要遍历两字符串一次。

• 空间复杂度：O(n)，其中 n 是字符串 needle 的长度。我们只需要保存字符串 needle 的前缀函数。

解法2：KMP算法（前缀表不减一）（建议）

class Solution {
public:
    int strStr(string haystack, string needle) {
        if (needle.length() == 0) {
            return 0;
        }
        vector next(needle.length());
        // 1、求 needle 部分的前缀表，我们需要保留这部分的前缀函数值。
        // 注意i从1开始，j从0开始。i指向后缀末尾位置，j指向前缀末尾位置。
        for(int i = 1,j= 0; i < needle.length(); i++) { 
            while (j > 0 && needle[i] != needle[j]) { // 前后缀不相同了（j>0 不带=）
                j = next[j-1]; // 向前回退
            }
            if (needle[i] == needle[j]) { // 找到相同的前后缀
                j++;   //同时向后移动i 和j 
            }
            next[i] = j; // next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
        }       
      
        // 2、求 haystack 部分的前缀函数，我们无需保留这部分的前缀函数值，只需要用一个变量记录上一个位置的前缀函数值即可。
        // 注意i就从0开始，j从0开始（因为next数组里记录的起始位置为0）。
        // i指向文本串起始位置，j 指向模式串起始位置。
        for (int i = 0,j = 0; i < haystack.length(); i++) { 
            while(j > 0 && haystack[i] != needle[j]) { // 不匹配
                j = next[j-1]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j]) { // 匹配，j和i同时向后移动
                j++; // 同时向后移动i 和j，i的增加在for循环里
            }
            // j指向了模式串needle的末尾，说明文本串haystack里出现了模式串needle
            if (j == needle.length() ) { 
                // 返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。
                return (i - needle.length() + 1);
            }
        }
        return -1;
    }
};

• 时间复杂度：O(m+n)，我们至多需要遍历两字符串一次。

• 空间复杂度：O(n)，其中 n 是字符串 needle 的长度。我们只需要保存字符串 needle 的前缀函数。

解法3：暴力

class Solution {
public:
    int strStr(string haystack, string needle) {
       int m=haystack.size(),n=needle.size();
       //当 needle 是空字符串时,我们应当返回 0 
       if(n==0){return 0;}       
       //此处应该带等号，考虑两个字符串都只含有一个字符
       for(int i=0;i+n<=m;i++){   //所有长度为needle.size()的字符串匹配一次
           bool flag=true;
           for(int j=0;j

• 时间复杂度：O(mn)，最坏情况下我们需要将字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。

• 空间复杂度：O(1)，只需要常数的空间保存若干变量。

8.重复的子字符串

 解法1：KMP算法（前缀表统一减一）

class Solution {
public:
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {         //字符串为空，则返回false
            return false;
        }
        vector next(s.length(),-1);
        for(int i = 1,j=-1;i < s.length(); i++){       //注意这里从1开始
            while(j >= 0 && s[i] != s[j+1]) {   //前后缀不相同
                j = next[j];                  //向前后退
            }
            if(s[i] == s[j+1]) {    //找到相同的前后缀
                j++;
            }
            next[i] = j;     //将j（前缀的长度）赋予给next[i]
        }
        int len = s.length();
        //next[len - 1] != -1，说明字符串有最长相同的前后缀
        //最长相等前后缀的长度为：next[len - 1] + 1
        //len % (len - (next[len - 1] + 1)) == 0 ，说明有该字符串有重复的子字符串
        return next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0;
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。

• 空间复杂度：O(n)，其中 n 是字符串 s 的长度。

 解法2：KMP（前缀表不减一）

class Solution {
public:
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {         //字符串为空，则返回false
            return false;
        }
        vector next(s.length(),0);
        for(int i = 1,j=0;i < s.length(); i++){       //注意这里从1开始
            while(j > 0 && s[i] != s[j]) {   //前后缀不相同
                j = next[j-1];                  //向前后退
            }
            if(s[i] == s[j]) {    //找到相同的前后缀
                j++;
            }
            next[i] = j;     //将j（前缀的长度）赋予给next[i]
        }
        int len = s.length();
        //next[len - 1] != 0，说明字符串有最长相同的前后缀
        //最长相等前后缀的长度为：next[len - 1]
        //len % (len - next[len - 1]) == 0 ，说明有该字符串有重复的子字符串
        return next[len - 1] != 0 && len % (len - next[len - 1] ) == 0;
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。

• 空间复杂度：O(n)，其中 n 是字符串 s 的长度。

9.长按键入

 解法1：双指针

思路：字符串 typed 的每个字符，有且只有两种「用途」：（1）作为 name 的一部分。此时会「匹配」name 中的一个字符  （2）作为长按键入的一部分。此时它应当与前一个字符相同。

class Solution {
public:
    bool isLongPressedName(string name, string typed) {
        int i=0,j=0;
        while(j0 && typed[j]==typed[j-1]){
                //如果 typed[j]=typed[j−1]，说明存在一次长按键入，此时只将 j 加 1
                ++j;
            }else{
                return false;
            }
        }
        return i==name.size();
    }
};

• 时间复杂度：O(m+n)，其中m ，n 分别是两个字符串的长度。

• 空间复杂度：O(1)。

10.*岛屿数量

 

解法1：深度优先搜索

 思路：将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。

深度优先搜索：以位置 1 为起始节点开始进行深度优先搜索，每个搜索到的 1 都会被重新标记为 0。最终岛屿的数量就是我们进行深度优先搜索的次数。

class Solution {
private:
    void dfs(vector>& grid,int r,int c){
        int row=grid.size();
        int col=grid[0].size();
        grid[r][c]='0';
        if(r-1>=0 && grid[r-1][c]=='1')  dfs(grid,r-1,c);
        if(r+1=0 && grid[r][c-1]=='1')  dfs(grid,r,c-1);
        if(c+1>& grid) {
        int row=grid.size();
        int col=grid[0].size();
        if(!row) return 0;
        int ans=0;
        for(int r=0;r

• 时间复杂度：O(mn)，其中 m 和 n 分别为行数和列数。

• 空间复杂度：O(mn)，在最坏情况下，整个网格均为陆地，深度优先搜索的深度达到 mn。

解法2：广度优先搜索

 思路：将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。

广度优先搜索：如果一个位置为 1，则将其加入队列，开始进行广度优先搜索。在广度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0。直到队列为空，搜索结束。最终岛屿的数量就是我们进行广度优先搜索的次数。

class Solution {
public:
    int numIslands(vector>& grid) {
        int row=grid.size();
        int col=grid[0].size();
        if(!row) return 0;
        int ans=0;
        for(int r=0;r> que;
                    que.push({r,c});

                    while(!que.empty()){ //直到队列为空，搜索结束
                        auto rc=que.front();
                        que.pop();
                        int nr=rc.first,nc=rc.second;
                        if(nr-1>=0 && grid[nr-1][nc]=='1'){
                            que.push({nr-1,nc});
                            grid[nr-1][nc]='0';
                        }
                        if(nr+1=0 && grid[nr][nc-1]=='1'){
                            que.push({nr,nc-1});
                            grid[nr][nc-1]='0';
                        }
                        if(nc+1

• 时间复杂度：O(mn)，其中 m 和 n 分别为行数和列数。

• 空间复杂度：O(min(m,n))，在最坏情况下，整个网格均为陆地，队列的大小可以达到 min⁡(m,n)。

11.岛屿的最大面积

 解法1：深度优先搜索

class Solution {
    int dfs(vector>& grid, int r, int c) {
        if (r < 0 || c < 0 || r == grid.size() || c == grid[0].size() || grid[r][c] != 1) {
            return 0;
        }
        // 为了确保每个土地访问不超过一次，我们每次经过一块土地时，将这块土地的值置为 0。这样我们就不会多次访问同一土地。
        grid[r][c] = 0;   
        // 在一个土地上，以4个方向探索与之相连的每一个土地（以及与这些土地相连的土地），那么探索过的土地总数将是该连通形状的面积。 
        int di[4] = {0, 0, 1, -1};
        int dj[4] = {1, -1, 0, 0};
        int ans = 1;
        for (int idx = 0; idx != 4; ++idx) {
            int nextR = r + di[idx], nextC = c + dj[idx];
            ans += dfs(grid, nextR, nextC);
        }
        return ans;
    }
public:
    int maxAreaOfIsland(vector>& grid) {
        int ans = 0;
        for (int i = 0; i != grid.size(); ++i) {
            for (int j = 0; j != grid[0].size(); ++j) {
                ans = max(ans, dfs(grid, i, j));
            }
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别为行数和列数。

• 空间复杂度：O(mn)，递归的深度最大可能是整个网格的大小，因此最大可能使用 O(mn)的栈空间。

12.*实现Trie（前缀树）

 

 解法1：前缀树

思路：前缀树：每个节点包含以下字段：1、指向子节点的指针数组 children。对于本题而言，数组长度为 26，即小写英文字母的数量。此时 children[0] 对应小写字母 a，children[1] 对应小写字母 b，…，children[25] 对应小写字母 z。2、布尔字段 isEnd。  表示该节点是否为字符串的结尾。

class Trie {
private:
    Trie *searchPrefix(string prefix){
        Trie *node=this;
        for(char ch:prefix){
            ch-='a';
            //情况1：子节点不存在。说明字典树中不包含该前缀，返回空指针
            if(node->children[ch]==nullptr){
                return nullptr;
            }
            //情况2：子节点存在。沿着指针移动到子节点，继续搜索下一个字符
            node=node->children[ch];
        }
        return node;
    }
    vector children;
    bool isEnd;
public:
    Trie() :children(26),isEnd(false){}    
    void insert(string word) {
        Trie *node=this;
        for(char ch:word){
            ch-='a';
            //情况1：子节点不存在
            if(node->children[ch]==nullptr){
                //创建一个新的子节点，记录在 children 数组的对应位置上
                node->children[ch]=new Trie();
            }
            //情况2：子节点存在。沿着指针移动到子节点，继续处理下一个字符
            node=node->children[ch];
        }
        //处理字符串的最后一个字符，然后将当前节点标记为字符串的结尾
        node->isEnd=true;
    }    
    bool search(string word) {
        Trie *node=this->searchPrefix(word);
        //搜索到前缀末尾，且前缀末尾对应节点的 isEnd 为真，则说明字典树中存在该字符串
        return node!=nullptr && node->isEnd;
    }   
    bool startsWith(string prefix) {
        //若搜索到了前缀的末尾，就说明字典树中存在该前缀
        return this->searchPrefix(prefix) !=nullptr;
    }
};
/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

• 时间复杂度：初始化为 O(1)，其余操作为 O(|S|)，其中 |S| 是每次插入或查询的字符串的长度。

• 空间复杂度：O(|T|)，其中 |T| 为所有插入字符串的长度之和。

13.#表示数值的字符串（自动机）

14.字符串转换整数（atoi）（自动机）

 

 

 

15.#把字符串转换成整数

 

16.比较版本号

解法一：双指针

class Solution {
public:
    int compareVersion(string version1, string version2) {
        int n = version1.length(), m = version2.length();
        int i = 0, j = 0;
        while (i < n || j < m) {
            int x = 0;
            for (; i < n && version1[i] != '.'; ++i) {
                x = x * 10 + (version1[i] - '0');
            }
            ++i; // 跳过点号
            int y = 0;
            for (; j < m && version2[j] != '.'; ++j) {
                y = y * 10 + (version2[j] - '0');
            }
            ++j; // 跳过点号
            if (x != y) {
                return x > y ? 1 : -1;
            }
        }
        return 0;
    }
};

题型五：栈与队列

 1.用栈实现队列

 解法1：双栈

 队列 queue 是一种 先进先出（first in - first out，FIFO）的数据结构：队列中的元素都从后端（rear）入队（push），从前端（front）出队（pop）。
栈  stack 是一种 后进先出（last in - first out，LIFO）的数据结构：栈中元素从栈顶（top）压入（push)，也从栈顶弹出（pop）。

class MyQueue {
private:
    //将栈1的数据移到栈2
    void stack1tostack2(){
        while(!stack1.empty()){
            stack2.push(stack1.top());
            stack1.pop();
        }
    }
    //stack1用于输入栈，压入push传入的数据；
    //stsck2用于输出栈，pop和peek操作
     stack stack1,stack2;
public:
    MyQueue() {}   //使用默认构造函数
    
    void push(int x) {
         stack1.push(x);
    }
    
    int pop() {
        if(stack2.empty()){
            stack1tostack2();
        }
        int x=stack2.top();
        stack2.pop();     //删除队列开头，
        return x;         //并返回元素
    }
    
    //返回队列开头的元素
    int peek() {
       if(stack2.empty()){
           stack1tostack2();
       }
       return stack2.top();
    }
    
    bool empty() {
       return stack1.empty() && stack2.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

2.#用两个栈实现队列

 解法1：双栈

class CQueue {
private:
    void stk1Tostk2(){
        while(!stk1.empty()){
            stk2.push(stk1.top());
            stk1.pop();
        }
    }
    stack stk1,stk2;
public:
    CQueue() {}    
    void appendTail(int value) {
        stk1.push(value);
    }    
    int deleteHead() {
        if(stk2.empty()){//(1)如果 stack2 为空，则将 stack1 里的所有元素弹出插入到 stack2 里
            stk1Tostk2();
        }
        if(stk2.empty()){//(2)如果 stack2 仍为空，则返回 -1，否则从 stack2 弹出一个元素并返回
            return -1;
        }else{
            int x=stk2.top();
            stk2.pop();
            return x;
        }
    }
};
/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue* obj = new CQueue();
 * obj->appendTail(value);
 * int param_2 = obj->deleteHead();
 */

3.用队列实现栈

解法1：双队列

class MyStack {
private: 
    //queue1用于存储栈内元素，queue2用于入栈操作的辅助队列
    queuequeue1,queue2;   
public:
    MyStack() {}   
    void push(int x) {
       queue2.push(x);     //先进相当于栈顶
       while(!queue1.empty()){
           queue2.push(queue1.front());
           queue1.pop();
       }
       swap(queue1,queue2);   //因为queue1 是用于存储的，交换，将queue2置空
    }
    
    int pop() {
       int x=queue1.front();
       queue1.pop();
       return x;
    }
    
    int top() {
        return queue1.front();
    }
    
    bool empty() {
       return queue1.empty();
    }
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

解法2：单队列

class MyStack {
private: 
    queue q;
public:
    MyStack() {}   
    void push(int x) {
        int n=q.size();
        q.push(x);
        for(int i=0;ipush(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

4.*有效的括号

 解法1：栈

class Solution {
public:
    bool isValid(string s) {
        stack stk;
        for (int i = 0; i < s.length(); i++) {
            //左括号入栈
            if (s[i] == '(') {
                stk.push(')');
            }else if (s[i] == '{'){
                stk.push('}');
            }else if (s[i] == '['){
                stk.push(']');
            }
            // 第二种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号 return false
            // 第三种情况：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所以return false
            else if (stk.empty() || stk.top() != s[i]) return false;
            else stk.pop();   // st.top() 与 s[i]相等，栈弹出元素
        }
        // 第一种情况：此时我们已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false，否则就return true
        return stk.empty();
    }
}

解法2：栈+哈希

class Solution {
public:
    bool isValid(string s) {
       int n=s.length();
       //有效字符串的长度一定是偶数
       if(n%2==1){
           return false;
       }
       //为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。
       //哈希表的键为右括号，值为相同类型的左括号。
       unordered_map pairs={
            {')','('},
            {']','['},
            {'}','{'}
           };
        //先出现的左括号后匹配，即先进后出，可以使用栈
        //由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶
       stack stk;
       for(char ch:s){
           if(pairs.count(ch)){    //右括号判断是否匹配
               if(stk.empty()|| stk.top()!=pairs[ch]){
                   return false;
               }
               stk.pop();   //匹配成功需要出栈
           }else{
               stk.push(ch);          //左括号入栈等待匹配
           }
       }
       return stk.empty();   //完全匹配的要求是栈为空
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。

• 空间复杂度：O(n+∣Σ∣)，其中 n 是字符串 s 的长度。其中 Σ 表示字符集，本题中字符串只包含 6 种括号，∣Σ∣=6。栈中的字符数量为 O(n)，而哈希表使用的空间为 O(∣Σ∣)，相加即可得到总空间复杂度。

5.有效的括号字符串

解法1：栈

class Solution {
public:
    bool checkValidString(string s) {
        stack leftstk,stk;
        for(int i=0;i Idx) return false;
        }

        return leftstk.empty();
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。需要遍历字符串一次，遍历过程中每个字符的操作时间都是 O(1)，遍历结束之后对左括号栈和星号栈弹出元素的操作次数不会超过 n。

• 空间复杂度：O(n)，其中 n 是字符串 s 的长度。空间复杂度主要取决于左括号栈和星号栈，两个栈的元素总数不会超过 n。

解法2：贪心

 思路：在遍历过程中维护未匹配的左括号数量可能的最小值和最大值，根据遍历到的字符更新最小值和最大值：

    如果遇到左括号，则将最小值和最大值分别加 1；

    如果遇到右括号，则将最小值和最大值分别减 1；

    如果遇到星号，则将最小值减 1，将最大值加 1。

任何情况下，未匹配的左括号数量必须非负，因此当最大值变成负数时，说明没有左括号可以和右括号匹配，返回 false。

当最小值为 0 时，不应将最小值继续减少，以确保最小值非负。

遍历结束时，所有的左括号都应和右括号匹配，因此只有当最小值为 0 时，字符串 s 才是有效的括号字符串

class Solution {
public:
    bool checkValidString(string s) {
        int minCount = 0, maxCount = 0;
        int n = s.size();
        for (int i = 0; i < n; i++) {
            char c = s[i];
            if (c == '(') {
                minCount++;
                maxCount++;
            } else if (c == ')') {
                minCount = max(minCount - 1, 0);
                maxCount--;
                if (maxCount < 0) {
                    return false;
                }
            } else {
                minCount = max(minCount - 1, 0);
                maxCount++;
            }
        }
        return minCount == 0;
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度。

• 空间复杂度：O(1)。

6.*最长有效括号

 解法1：栈

class Solution {
public:
    int longestValidParentheses(string s) {
        int ans=0;
        stack stk;   //栈中放入每个左括号的下标
        stk.push(-1);     //栈底放入遍历过的最后一个没有被匹配的右括号的下标，为了保持一致
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是给定字符串的长度。我们只需要遍历字符串一次即可。

• 空间复杂度：O(n)， 栈的大小在最坏情况下会达到 n。

 解法2：正向遍历+反向遍历

class Solution {  
public:
    //正反遍历两边字符串
    int longestValidParentheses(string s) {
        int left=0,right=0,ans=0;
        //从左往右遍历
        for(int i=0;i=0;--i){
            if(s[i]=='('){
                left++;
            }else{
                right++;
            }

            if(left==right){
                ans=max(ans,2*left);
            }else if(right

• 时间复杂度：O(n)，其中 n 是给定字符串的长度。

• 空间复杂度：O(1)， 我们只需要常数空间存放若干变量 n。

解法3：动态规划

思路：dp[i] 表示以下标 i 字符结尾的最长有效括号的长度

有效的子串一定以 右括号 结尾，因此我们可以知道以 左括号 结尾的子串对应的 dp 值必定为 0 ，我们只需要求解 右括号 在 dp 数组中对应位置的值。

class Solution {
public:
    int longestValidParentheses(string s) {
        int ans=0,n=s.length();
        vector dp(n,0);   //里面是int类型，而不是char
        for(int i=1;i=2 ? dp[i-2] : 0) +2;
                }else if(i-dp[i-1]>0 && s[i-dp[i-1]-1] =='('){
                    //情况2：s[i]=‘)’ 且 s[i−1]=‘)’  且 s[i−dp[i−1]−1]=‘(’，那么  dp[i]=dp[i−1]+dp[i−dp[i−1]−2]+2
                    dp[i]=dp[i-1] + ( (i-dp[i-1]) >=2 ? dp[i-dp[i-1]-2] : 0) +2;
                }
                ans=max(ans,dp[i]);
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是给定字符串的长度。只需遍历整个字符串一次，即可将 dp 数组求出来。

• 空间复杂度：O(n)， 需要一个大小为 n 的 dp 数组。

7.*删除无效的括号

 解法1：回溯

class Solution {
private:
    void backTracking(string str,int start,int lRemove,int rRemove){
        if(lRemove==0 && rRemove==0){
            if(isValid(str)){
                ans.push_back(str);
            }
            return;
        }
        for(int i=start;i str.size()-i){
                return;
            }
            //去重：如果遇到连续相同的括号我们只需要搜索一次即可
            if(i!=start && str[i]==str[i-1])  continue;
            // 尝试去掉一个左括号
            if(lRemove>0 && str[i]=='('){
                //s.substr(pos, n)：返回一个string，包含s中从pos开始的n个字符的拷贝
                //只加参数pos,会从pos位置开始拷贝剩余全部字符
                backTracking(str.substr(0,i)+str.substr(i+1), i, lRemove-1, rRemove);
            }
            // 尝试去掉一个右括号
            if(rRemove>0 && str[i]==')'){
                backTracking(str.substr(0,i)+str.substr(i+1), i, lRemove, rRemove-1);
            }
        }
    }

    bool isValid(const string &str){  //左右括号数量相等，才会是有效字符串
        int count=0;
        for(int i=0;i ans;
public:
      vector removeInvalidParentheses(string s) {
        int lRemove=0,rRemove=0;
        for(char c:s){
            if(c=='('){
                lRemove++;
            }else if(c==')'){
                if(lRemove==0){
                    rRemove++;
                }else{
                    lRemove--;
                }
            }
       }
       backTracking(s,0,lRemove,rRemove);
       return ans;
    }
};

• 时间复杂度：O(n×2^n)，其中 n 为字符串的长度。考虑到一个字符串最多可能有 2^n 个子序列，每个子序列可能需要进行一次合法性检测。

• 空间复杂度：O(n^2)，其中 n 为字符串的长度。返回结果不计入空间复杂度，考虑到递归调用栈的深度，并且每次递归调用时需要复制字符串一次，因此空间复杂度为 O(n^2)。

8.删除字符串中的所有相邻重复项

 解法1：栈

 思路：创建一个栈，然后结果转化为字符串输出

class Solution {
public:
    string removeDuplicates(string s) {
      stack stk;
      for(char &ch:s){
         if(!stk.empty() && ch==stk.top()){   //字符串使用的是back(),栈使用的是top()
             stk.pop();
         }
         else stk.push(ch);
      }

      string ans="";      //字符串要用双引号
      while(!stk.empty()){
          ans+=stk.top();
          stk.pop();
      }
      reverse(ans.begin(),ans.end());
      return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是字符串的长度。只需遍历整个字符串一次。

• 空间复杂度：O(n)，主要是栈占用的空间。

 解法2：栈（官方）

思路：在 C++ 代码中，由于 std::string 类本身就提供了类似「入栈」和「出栈」的接口，因此我们直接将需要被返回的字符串作为栈即可。

class Solution {
public:
    string removeDuplicates(string s) {
      string stk;
      for(char &ch:s){
         if(!stk.empty() && ch==stk.back()){
             stk.pop_back();
         }
         else stk.push_back(ch);
      }
      return stk;
    }
};

• 时间复杂度：O(n)，其中 n 是字符串的长度。只需遍历整个字符串一次。

• 空间复杂度：O(1)

9.逆波兰表达式求值

 

解法1：栈

思路：使用一个栈存储操作数，从左到右遍历逆波兰表达式：如果遇到操作数，则将操作数入栈；如果遇到运算符，则将两个操作数出栈，其中先出栈的是右操作数，后出栈的是左操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数入栈。整个逆波兰表达式遍历完毕之后，栈内只有一个元素，该元素即为逆波兰表达式的值。 

class Solution {
public:
    int evalRPN(vector& tokens) {
       stack stk;
       for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组 tokens 的长度。需要遍历数组 tokens一次，计算逆波兰表达式的值。

• 空间复杂度：O(n)，使用栈存储计算过程中的数，栈内元素个数不会超过逆波兰表达式的长度。

解法2：栈（官方）

class Solution {
public:
    bool isNumber(string& token){
        return !(token=="+"||token=="-"||token=="*"||token=="/");  //字符串，必是双引号
    }

    int evalRPN(vector& tokens) {
       stack stk;
       for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组 tokens 的长度。需要遍历数组 tokens一次，计算逆波兰表达式的值。

• 空间复杂度：O(n)，使用栈存储计算过程中的数，栈内元素个数不会超过逆波兰表达式的长度。

10. *滑动窗口最大值

解法1：单调队列

 双端队列deque函数，支持高效插入和删除容器的头部元素，支持高效插入和删除容器的头部元素。

void push_front(const T& x):双端队列头部增加一个元素X

void push_back(const T& x):双端队列尾部增加一个元素x

队列queue 常见用法：

1. push()  在队尾插入一个元素
2. pop()   删除队列第一个元素
3. size()  返回队列中元素个数
4. empty() 如果队列空则返回true
5. front()   返回队列中的第一个元素
6. back()   返回队列中最后一个元素

class Solution {
private:
    class MyQueue { //单调队列（从大到小）
    public:
        deque que; // 使用deque来实现单调队列
        void pop(int value) {
            // 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，同时pop之前判断队列当前是否为空。
            if (!que.empty() && value == que.front()) {
                que.pop_front();             //如果相等则弹出。
            }
        }
        // 如果push的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到push的数值小于等于队列入口元素的数值为止。
        // 这样就保持了队列里的数值是单调从大到小的了。
        void push(int value) {
            while (!que.empty() && value > que.back()) {
                que.pop_back();
            }
            que.push_back(value);
        }
        // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
        int front() {
            return que.front();
        }
    };
public:
    vector maxSlidingWindow(vector& nums, int k) {
        MyQueue que;
        vector ans;
        for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
            que.push(nums[i]);
        }
        ans.push_back(que.front()); // ans 记录前k的元素的最大值
        for (int i = k; i < nums.size(); i++) {
            que.pop(nums[i - k]);  // 滑动窗口移除最前面元素
            que.push(nums[i]);     // 滑动窗口前加入最后面的元素
            ans.push_back(que.front()); // 记录对应的最大值
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。

• 空间复杂度：O(k)，我们使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素，因此队列使用的空间为 O(k)。

解法2：单调队列（官方）

class Solution {
public:
    vector maxSlidingWindow(vector& nums, int k) {
       deque dq;   //记录下标
       for(int i=0;i=nums[dq.back()]){
               dq.pop_back();
           }
           dq.push_back(i);    //推入 i 
       }

       vector ans={nums[dq.front()]};
       for(int i=k;i=nums[dq.back()]){
               dq.pop_back();
           }
           dq.push_back(i);
           //删除队首的元素，保证队列长度不超过k
           while(dq.front()<=i-k){
               dq.pop_front();
           }
           ans.push_back(nums[dq.front()]);    //队首下标对应的元素就是滑动窗口中的最大值
       }
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。

• 空间复杂度：O(k)，我们使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素，因此队列使用的空间为 O(k)。

解法3：优先队列

class Solution {
public:
    vector maxSlidingWindow(vector& nums, int k) {
        int n = nums.size();
        priority_queue> q;   //优先队列 priority_ 不能省

        for (int i = 0; i < k; ++i) {
            q.emplace(nums[i], i);  //元素和元素在数组中的下标
        }

        vector ans = {q.top().first};     //堆顶的元素就是堆中所有元素的最大值

        for (int i = k; i < n; ++i) {
            q.emplace(nums[i], i);

            while (q.top().second <= i - k) {   //重点理解
                q.pop();
            }
            ans.push_back(q.top().first);

        }
        return ans;
    }
};

• 时间复杂度：O(nlogn)，其中 n 是数组 nums 的长度。在最坏情况下，数组 nums 中的元素单调递增，那么最终优先队列中包含了所有元素，没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O(log⁡n)，因此总时间复杂度为 O(nlog⁡n)。

• 空间复杂度：O(n)，即为优先队列需要使用的空间。

11.#滑动窗口的最大值

 解法1：单调队列

class Solution {
private:
    class MyQueue { //单调队列（从大到小）
    public:
        deque que; // 使用deque来实现单调队列
        void pop(int value) {
            // 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，同时pop之前判断队列当前是否为空。
            if (!que.empty() && value == que.front()) {
                que.pop_front();             //如果相等则弹出。
            }
        }
        // 如果push的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到push的数值小于等于队列入口元素的数值为止。
        // 这样就保持了队列里的数值是单调从大到小的了。
        void push(int value) {
            while (!que.empty() && value > que.back()) {
                que.pop_back();
            }
            que.push_back(value);
        }
        // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
        int front() {
            return que.front();
        }
    };
public:
    vector maxSlidingWindow(vector& nums, int k) {
        if(nums.size()==0) return {};//重要
        MyQueue que;
        vector ans;
        for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
            que.push(nums[i]);
        }
        ans.push_back(que.front()); // ans 记录前k的元素的最大值
        for (int i = k; i < nums.size(); i++) {
            que.pop(nums[i - k]);  // 滑动窗口移除最前面元素
            que.push(nums[i]);     // 滑动窗口前加入最后面的元素
            ans.push_back(que.front()); // 记录对应的最大值
        }
        return ans;
    }
};

12.#队列的最大值

 解法1：暴力

class MaxQueue {
private:
    int begin=0,end=0;
    int que[20000];
public:
    MaxQueue() {}
    
    int max_value() {
        int ans=-1;
        for(int i=begin;imax_value();
 * obj->push_back(value);
 * int param_3 = obj->pop_front();
 */

• 时间复杂度：O(1)（插入，删除），O(n)（求最大值）。插入与删除只需要普通的队列操作，为 O(1)，求最大值需要遍历当前的整个队列，最坏情况下为 O(n)。

• 空间复杂度：O(n)，需要用队列存储所有插入的元素。

解法2：单调的双端队列

class MaxQueue {
    queue q;
    deque d;
public:
    MaxQueue() {
    }
    
    int max_value() {
        if (d.empty())
            return -1;
        return d.front();
    }
    
    void push_back(int value) {
        while (!d.empty() && d.back() < value) {
            d.pop_back();
        }
        d.push_back(value);
        q.push(value);
    }
    
    int pop_front() {
        if (q.empty())
            return -1;
        int ans = q.front();
        if (ans == d.front()) {
            d.pop_front();
        }
        q.pop();
        return ans;
    }
};

13.*前 K 个高频元素

解法1：小顶堆+优先队列+哈希

堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆，即大顶堆（堆头是最大元素），小顶堆（堆头是最小元素）。

优先级队其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。而且优先级队列内部元素是自动依照元素的权值排列。

优先队列包括头文件#include , 和queue不同的就在于可以自定义其中数据的优先级, 让优先级高的排在队列前面,优先出队

定义：priority_queue
Type 就是数据类型，Container 就是容器类型（Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list。STL里面默认用的是vector），Functional 就是比较的方式，当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆

priority_queue a;   // 对于基础类型 默认是大顶堆
//等同于
priority_queue, less > a;   // 降序队列
     
priority_queue, greater > b;  //小顶堆

我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

class Solution {
public:
    // 重写仿函数方式，实现一个小顶堆
    class minHeap{
        public:
              bool operator()(const pair &m, const pair &n){
                  return m.second>n.second;  // 结果为true，n的优先级高
              }
    };
    vector topKFrequent(vector& nums, int k) {
       //1、利用map统计元素出现的频率,  map
       unordered_map map;
       for(auto &num:nums){
           map[num]++;
       }

       //2、对频率进行排序，定义一个小顶堆（堆头是最小元素），大小是k
       //   借用优先队列实现，从小到大
       // pair 的第一个元素代表数组的值，第二个元素代表了该值出现的次数
       priority_queue, vector>, minHeap>  pq;   //类名后怎么不加（）

       for(auto it=map.begin();it!=map.end();++it){
           pq.push(*it);
           // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
           if(pq.size()>k){
               pq.pop();
           }
       }

       // 3、找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒叙来输出到数组
       vector ans;
       while(!pq.empty()){
           ans.emplace_back(pq.top().first);  // top访问堆头元素
           pq.pop();   // pop() 弹出堆头元素
       }
       return ans;
    }
};

• 时间复杂度：O(nlogk)，其中 n 是数组 nums 的长度。我们首先遍历原数组，并使用哈希表记录出现次数，每个元素需要 O(1) 的时间，共需 O(n) 的时间。随后，我们遍历「出现次数数组」，由于堆的大小至多为 k，因此每次堆操作需要 O(log⁡k) 的时间，共需 O(nlog⁡k) 的时间。二者之和为 O(nlog⁡k)。

• 空间复杂度：O(n)，哈希表的大小为 O(n)，而堆的大小为 O(k)，共计为 O(n)。

14.*数组中的第K个最大元素

 解法1：堆排序

class Solution {
public:
    //大顶堆，建堆
    void maxHeap(vector &a,int i,int heapsize){
        int m=i*2+1,n=i*2+2,largest=i; 
        // 如果左子点在数组内，且比当前父节点大，则将最大值的指针指向左子点  
        if(ma[largest]){
            largest=m;
        }
        if(na[largest]){
            largest=n;
        }
        // 如果最大值的指针不是父节点，则交换父节点和当前最大值指针指向的子节点
        if(largest!=i){
            swap(a[i],a[largest]);
            // 由于交换了父节点和子节点，因此可能对子节点的子树造成影响，所以对子节点的子树进行调整
            maxHeap(a,largest,heapsize);
        }
    }
    //大顶堆，调整
    void buildMaxHeap(vector &a,int heapsize){
        // 从最后一个父节点位置开始调整每一个节点的子树。
        // 数组长度为heasize，因此最后一个节点的位置为heapsize-1，所以父节点的位置为(heapsize-1-1)/2
        for(int i=(heapsize-2)/2;i>=0;--i){
            maxHeap(a,i,heapsize);
        }
    }

    int findKthLargest(vector& nums, int k) {
      int heapsize=nums.size();
      buildMaxHeap(nums,heapsize);
      for(int i=nums.size()-1; i>=nums.size()-k+1;--i){      //k-1次删除操作后，堆顶元素就是我们要找的答案
          // 将堆顶元素与最后一个元素交换，即大顶堆的删除堆顶元素的操作，数量减一
          swap(nums[0],nums[i]); 
          --heapsize;
          // 从堆头处开始修正大顶堆
          maxHeap(nums,0,heapsize);
      }
      return nums[0];
    }
};

• 时间复杂度：O(nlog⁡n)，建堆的时间代价是 O(n)，删除的总代价是 O(klog⁡n)，因为 k

• 空间复杂度：O(log⁡n)，即递归使用栈空间的空间代价。

解法2：sort函数排序

class Solution {
public:
    int findKthLargest(vector& nums, int k) {
       sort(nums.begin(),nums.end(),greater());
       return nums[k-1];
    }
};

15.#最小的k个数

 解法1：sort函数排序

class Solution {
public:
    vector getLeastNumbers(vector& arr, int k) {
        vector ans(k, 0);
        sort(arr.begin(), arr.end());
        /*for (int i = 0; i < k; ++i) {
            ans[i] = arr[i];
        }*/
        ans.assign(arr.begin(),arr.begin()+k);
        return ans;
    }
};

• 时间复杂度：O(nlog⁡n)，其中 n 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂度。

• 空间复杂度：O(log⁡n)，排序所需额外的空间复杂度为 O(log⁡n)。

16.数据流的中位数

 

 解法1：堆+优先队列

class MedianFinder {
private:
    //降序队列，大顶堆：存放小于中位数的数据，堆顶为最大元素
    priority_queue,less> maxHeap; 
    //升序队列，小顶堆：存放大于中位数的数据，堆顶为最小元素
    priority_queue,greater> minHeap; 
public:
    /** initialize your data structure here. */
    MedianFinder() {}  

    // 维持堆数据平衡，并保证左边堆的最大值 <= 右边堆的最小值 
    void addNum(int num) {
        if(maxHeap.size() == minHeap.size()){
            // 两堆的数量相等时，小顶堆添加元素：为防止元素可能属于大顶堆的，因此不是直接将元素加入小顶堆
            // 而是先将元素加入大顶堆后，再添加入小顶堆，并记得将大顶堆的堆顶元素删除
            maxHeap.push(num);
            minHeap.push(maxHeap.top());
            maxHeap.pop();
        }else{
            minHeap.push(num);
            maxHeap.push(minHeap.top());
            minHeap.pop();
        }
    }   
    double findMedian() {
        if(maxHeap.size() != minHeap.size()){
            return minHeap.top();  // 两堆元素相等，往小顶堆添加元素，所以奇数时一定是小顶堆的元素多
        }
        return (minHeap.top()+maxHeap.top())/2.0;
    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */

• 时间复杂度：addNum: O(log⁡n)，其中 n 为累计添加的数的数量。findMedian: O(1)。

• 空间复杂度：O(n)，主要为优先队列的开销。

17.#数据流中的中位数

 

 解法1：堆+优先队列

class MedianFinder {
private:
    priority_queue,less> maxHeap; 
    priority_queue,greater> minHeap; 
public:
    MedianFinder() {}  
    void addNum(int num) {
        if(maxHeap.size() == minHeap.size()){
            maxHeap.push(num);
            minHeap.push(maxHeap.top());
            maxHeap.pop();
        }else{
            minHeap.push(num);
            maxHeap.push(minHeap.top());
            minHeap.pop();
        }
    }   
    double findMedian() {
        if(maxHeap.size() != minHeap.size()){
            return minHeap.top();  
        }
        return (minHeap.top()+maxHeap.top())/2.0;
    }
};

• 时间复杂度：addNum: O(log⁡n)，其中 n 为累计添加的数的数量。findMedian: O(1)。

• 空间复杂度：O(n)，主要为优先队列的开销。

18.*最小栈

 

 解法1：栈

思路：因为栈是先进后出的，所以需要构建辅助栈。辅助栈：用于存储与每个元素对应的最小值，与元素栈同步插入与删除。

class MinStack {  
private:
    stack x_stack;
    stack min_stack;
public:
    //在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。
    MinStack() {
        min_stack.push(INT_MAX);
    }   
    //当一个元素要入栈时，我们取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；
    void push(int val) {
        x_stack.push(val);
        min_stack.push(min(min_stack.top(),val));
    }    
    //当一个元素要出栈时，我们把辅助栈的栈顶元素也一并弹出；
    void pop() {
        x_stack.pop();
        min_stack.pop();
    }  
    int top() {
        return x_stack.top();
    }   
    int getMin() {
        return min_stack.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();*/

• 时间复杂度：O(1)，因为栈的插入、删除与读取操作都是 O(1)，我们定义的每个操作最多调用栈操作两次。

• 空间复杂度：O(n)，其中 n 为总操作数。最坏情况下，我们会连续插入 n 个元素，此时两个栈占用的空间为 O(n)。

19.#包含min函数的栈

 解法1：栈

class MinStack {
private:
    stack x_stack,min_stack;
public:
    /** initialize your data structure here. */
    MinStack() {
        min_stack.push(INT_MAX);
    }
    
    void push(int x) {
        x_stack.push(x);
        min_stack.push(::min(min_stack.top(),x));
    }
    
    void pop() {
        x_stack.pop();
        min_stack.pop();
    }
    
    int top() {
        return x_stack.top();
    }
    
    int min() {
        return min_stack.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->min();
 */

20.*字符串解码

 解法1：栈

class Solution {
public:
    string getDigits(string &s, size_t &ptr) {
        string ret = "";
        while (isdigit(s[ptr])) {
            ret.push_back(s[ptr++]);
        }
        return ret;
    }
    string getString(vector  &v) {
        string ret;
        for (const auto &s: v) {
            ret += s;
        }
        return ret;
    }
    string decodeString(string s) {
        vector  stk;
        size_t ptr = 0;
        while (ptr < s.size()) {
            char cur = s[ptr];
            if (isdigit(cur)) {
                // 获取一个数字并进栈
                string digits = getDigits(s, ptr);
                stk.push_back(digits);
            } else if (isalpha(cur) || cur == '[') {
                // 获取一个字母并进栈
                stk.push_back(string(1, s[ptr++])); 
            } else {
                ++ptr;
                vector  sub;
                while (stk.back() != "[") {
                    sub.push_back(stk.back());
                    stk.pop_back();
                }
                reverse(sub.begin(), sub.end());
                // 左括号出栈
                stk.pop_back();
                // 此时栈顶为当前 sub 对应的字符串应该出现的次数
                int repTime = stoi(stk.back()); 
                stk.pop_back();
                string t, r = getString(sub);
                // 构造字符串
                while (repTime--) t += r; 
                // 将构造好的字符串入栈
                stk.push_back(t);
            }
        }
        return getString(stk);
    }
};

• 时间复杂度：O(S)，记解码后得出的字符串长度为 S，除了遍历一次原字符串 s，我们还需要将解码后的字符串中的每个字符都入栈，并最终拼接进答案中，故渐进时间复杂度为 O(S+|s|)，即 O(S)。

• 空间复杂度：O(S)，记解码后得出的字符串长度为 S，这里用栈维护 TOKEN，栈的总大小最终与 S 相同，故渐进空间复杂度为 O(S)。

解法2：递归

class Solution {   //涉及到编码原理：不懂
public:
    string src; 
    size_t ptr;
    int getDigits() {
        int ret = 0;
        while (ptr < src.size() && isdigit(src[ptr])) {
            ret = ret * 10 + src[ptr++] - '0';
        }
        return ret;
    }
    string getString() {
        if (ptr == src.size() || src[ptr] == ']') {
            // String -> EPS
            return "";
        }
        char cur = src[ptr]; int repTime = 1;
        string ret;
        if (isdigit(cur)) {
            // String -> Digits [ String ] String
            // 解析 Digits
            repTime = getDigits(); 
            // 过滤左括号
            ++ptr;
            // 解析 String
            string str = getString(); 
            // 过滤右括号
            ++ptr;
            // 构造字符串
            while (repTime--) ret += str; 
        } else if (isalpha(cur)) {
            // String -> Char String
            // 解析 Char
            ret = string(1, src[ptr++]);
        }       
        return ret + getString();
    }
    string decodeString(string s) {
        src = s;
        ptr = 0;
        return getString();
    }
};

• 时间复杂度：O(S)，记解码后得出的字符串长度为 S，除了遍历一次原字符串 s，我们还需要将解码后的字符串中的每个字符都拼接进答案中，故渐进时间复杂度为 O(S+|s|)，即 O(S)。

• 空间复杂度：O(|s|)，若不考虑答案所占用的空间，那么就只剩递归使用栈空间的大小，这里栈空间的使用和递归树的深度成正比，最坏情况下为 O(∣s∣)，故渐进空间复杂度为 O(|s|)。

21.验证栈序列

 

 解法1：辅助栈+模拟

思路：栈的所有数字均不相等 ，因此在循环入栈中，每个元素出栈的位置的可能性是唯一的（若有重复数字，则具有多个可出栈的位置）

class Solution {
public:
    bool validateStackSequences(vector& pushed, vector& popped) {
        stack stk;
        int i=0;
        for(int num:pushed){
            stk.push(num);
            while(!stk.empty() && stk.top()==popped[i]){
                //若 stack 的栈顶元素 = 弹出序列元素 popped[i] ，则执行出栈与 i++ ；
                stk.pop();
                i++;
            }
        }
        return stk.empty();//若 stack 为空，则此弹出序列合法。
    }
};

• 时间复杂度：O(n)，其中 n 为列表 pushed 的长度；每个元素最多入栈与出栈一次，即最多共 2n 次出入栈操作。

• 空间复杂度：O(n)，辅助栈 stack 最多同时存储 n 个元素。

22.#栈的压入、弹出序列

 解法1：辅助栈+模拟

class Solution {
public:
    bool validateStackSequences(vector& pushed, vector& popped) {
        stack stk; //辅助栈
        int i=0;
        for(int num:pushed){
            stk.push(num);
            while(!stk.empty() && stk.top()==popped[i]){
                //若 stack 的栈顶元素 = 弹出序列元素 popped[i] ，则执行出栈与 i++ ；
                stk.pop();
                i++;
            }
        }
        return stk.empty();//若 stack 为空，则此弹出序列合法。
    }
};

23.基础计算器

 

 解法1：栈

class Solution {
public:
    int calculate(string s) {
        int len=s.length();
        int sign=1;
        int ans=0;

        stack stk;
        stk.push(1);
        for(int i=0;i='0' && s[i]<='9'){
                    num=10*num+s[i]-'0';
                    i++;
                }
                ans+=sign*num;
            }
        }
        return ans;
    }
};

24.基础计算器II

 

解法1：栈

class Solution {
public:
    int calculate(string s) {
        int len=s.length();
        int num=0;
        vector stk;
        char pre='+';
        for(int i=0;i

25.行星碰撞

 解法1：栈

class Solution {
public:
    vector asteroidCollision(vector& asteroids) {
        vector stk;
        for(auto a:asteroids){
            if(a>0){
                stk.push_back(a);
            }else{
                bool exist=true;
                while(exist && !stk.empty() && stk.back()>0){
                    exist=stk.back() < -a;
                    if(stk.back()<= -a)  stk.pop_back();
                }
                if(exist)  stk.push_back(a);
            }
        }
        return stk;
    }    
};

题型六：单调栈

1.*每日温度

 解法1:单调栈

思路: 通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，

此时我们就要想到可以用   单调栈    时间复杂度 O(n)

单调栈中元素，从栈顶到栈底单调递增 (即栈底元素最大); 栈中只存放元素的下标 i

class Solution {
public:
    vector dailyTemperatures(vector& temperatures) {
        stack stk;
        vector ans(temperatures.size(),0);
        stk.push(0);
        for(int i=1;itemperatures[stk.top()]){//注意栈不能为空

                    ans[stk.top()]=i-stk.top();  // 栈中存放的是元素的下标

                    stk.pop();
                }
                stk.push(i);
            }
        }
        return ans;
    }
};

class Solution {
public:
    vector dailyTemperatures(vector& temperatures) {
        stack stk;
        vector ans(temperatures.size(),0);
        stk.push(0);
        for(int i=1;itemperatures[stk.top()]){
                    ans[stk.top()]=i-stk.top();
                    stk.pop();
                }
                stk.push(i);
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是温度列表的长度。正向遍历温度列表一遍，对于温度列表中的每个下标，最多有一次进栈和出栈的操作。
• 空间复杂度：O(n)，其中 n 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。

2.链表中的下一个更大的节点

解法1：单调栈

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    vector nextLargerNodes(ListNode* head) {
        stack stk;
        int len=0;
        vector vec;
        while(head){
            len++;
            vec.push_back(head->val);
            head=head->next;
        }
        vector ans(len,0);
        stk.push(0);
        for(int i=1;i vec[stk.top()]){
                ans[stk.top()]=vec[i];
                stk.pop();
            }
            stk.push(i);
        }
        return ans;
    }
};

3. 股票价格跨度

 解法1：单调栈

思路：价格序列prices维持一个栈顶到栈底单调递增的单调栈，ans 存储离上一个价格之间的天数

class StockSpanner {
public:
    stack stk,prices;
    StockSpanner() {}
      
    int next(int price) {
        int ans=1;
        while(!prices.empty() && price >= prices.top()){
            prices.pop();
            ans+=stk.top();
            stk.pop();
        }
        prices.push(price);
        stk.push(ans);
        return ans;
    }
};

/**
 * Your StockSpanner object will be instantiated and called as such:
 * StockSpanner* obj = new StockSpanner();
 * int param_1 = obj->next(price);
 */

4.最多能完成排序的块 

解法1：单调栈

思路：维护单调递增的单调栈，遍历每一个元素，如果当前元素大于栈顶元素说明找到了一个新的分段。如果当前元素小于栈顶元素，保存栈顶元素在栈中，最后返回栈中元素的个数即可。

class Solution {
public:
    int maxChunksToSorted(vector& arr) {
        stack stk;
        stk.push(0);
        for(int i=1; iarr[stk.top()]){
                stk.push(i);
                continue;
            }
            
            int mx=stk.top();
            while(!stk.empty() && arr[i] < arr[stk.top()]){
                stk.pop();
            }
            stk.push(mx);
        }
        return stk.size();
    }
};

解法2：贪心

class Solution {
public:
    int maxChunksToSorted(vector& arr) {
        int ans=0;
        int mx=0;
        for(int i=0;i

5.最多能完成排序的块II

 解法1：单调栈

class Solution {
public:
    int maxChunksToSorted(vector& arr) {
        stack stk;
        stk.push(0);
        for(int i=1; iarr[stk.top()]){
                stk.push(i);
                continue;
            }
            
            int mx=stk.top();
            while(!stk.empty() && arr[i] < arr[stk.top()]){
                stk.pop();
            }
            stk.push(mx);
        }
        return stk.size();
    }
};

6.下一个更大元素I

解法1：单调栈+哈希

class Solution {
public:
    vector nextGreaterElement(vector& nums1, vector& nums2) {
        stack stk;
        vector ans(nums1.size(),-1);

        //不重复的元素，利用哈希表存放nums1 的元素 ：key:下标元素，value：下标
        unordered_map umap;
        for(int i=0;inums2[stk.top()]){
                    //判断栈顶元素是否在nums1里出现过，（注意栈里的元素是nums2的元素），如果出现过，开始记录结果。
                    if(umap.count(nums2[stk.top()])>0){  // 看map里是否存在这个元素
                        int index=umap[nums2[stk.top()]];// 根据map找到nums2[stk.top()] 在 nums1中的下标
                        ans[index]=nums2[i];
                    }
                    stk.pop();
                }
                stk.push(i);
            }
        }
        return ans;
    }
};

class Solution {
public:
    vector nextGreaterElement(vector& nums1, vector& nums2) {
        stack stk;
        vector ans(nums1.size(),-1);
        unordered_map umap;
        for(int i=0;inums2[stk.top()]){
                    if(umap.count(nums2[stk.top()])>0){  // 看map里是否存在这个元素
                        int index=umap[nums2[stk.top()]];// 根据map找到nums2[stk.top()] 在 nums1中的下标
                        ans[index]=nums2[i];
                    }
                    stk.pop();
                }
                stk.push(i);
            }
        return ans;
    }
};

• 时间复杂度：O(m+n)，其中 m 是 nums1​ 的长度，n 是 nums2​ 的长度。我们需要遍历 nums2 以计算 nums2​ 中每个元素右边的第一个更大的值；需要遍历 nums1​ 以生成查询结果。
• 空间复杂度：O(n)，用于存储哈希表。

7.下一个更大元素II

解法1：单调栈 + 循环数组

class Solution {    //重点是如何处理循环数组
public:
    vector nextGreaterElements(vector& nums) {
        stack stk;
        int len=nums.size();
        vector ans(len,-1);
        for(int i=0;inums[stk.top()]){
                ans[stk.top()]=nums[i%len];
                stk.pop();
            }
            stk.push(i%len);
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是序列的长度。我们需要遍历该数组中每个元素最多 2 次，每个元素出栈与入栈的总次数也不超过 4 次。
• 空间复杂度：O(n)，其中 n 是序列的长度。空间复杂度主要取决于栈的大小，栈的大小至多为 2n−1。

8.*接雨水

解法1：双指针

class Solution { // 双指针按 列 记录雨水
public:
    int trap(vector& height) {
        int sum=0;
        int leftMax=0,rightMax=0;
        int left=0,right=height.size()-1;
        while(left

• 时间复杂度：O(n)，其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。
• 空间复杂度：O(1)，只需要使用常数的额外空间。

解法2：单调栈

class Solution {
public:
    int trap(vector& height) {
        stack stk;  //单调栈是按照行的方式来记录雨水的
        int ans=0;
        for(int i=0;iheight[stk.top()]  保证单调栈中，从栈顶到栈底是单调递增的
            while(!stk.empty() && height[i]>height[stk.top()]){
                //记栈顶元素为top，栈顶左边的元素下标 left, 栈顶右边的元素（即入栈的元素）下标 i
                int top=stk.top();
                stk.pop();   //为了得到 left，需要将 top 出栈。
                if(!stk.empty()){   //必须保证 非空
                    int left=stk.top();
                    int h=min(height[left],height[i]) - height[top];
                    int w=i-left-1; // 注意减一，只求中间宽度
                    ans+=h*w;
                }
            }
            stk.push(i);   //此处需要将元素下标入栈
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 height 的长度。从 0 到 n−1 的每个下标最多只会入栈和出栈各一次。
• 空间复杂度：O(n)，其中  是数组 height 的长度。空间复杂度主要取决于栈空间，栈的大小不会超过 n。

解法3：动态规划

class Solution {
public:
    int trap(vector& height) {
        int n=height.size();
        if(n<=2) return 0;
        // leftMax[i] 表示下标 i 及其左边的位置中，height 的最大高度
        // rightMax[i] 表示下标 i 及其右边的位置中，height 的最大高度
        // 1、记录每个柱子左边柱子最大高度
        vector leftMax(n);
        leftMax[0]=height[0];
        for(int i=1;i rightMax(n);
        rightMax[n-1]=height[n-1];
        for(int i=n-2;i>=0;--i){
            rightMax[i]=max(height[i],rightMax[i+1]);
        }
        // 3、求和
        int sum=0;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组 height 的长度。计算数组 leftMax 和 rightMax 的元素值各需要遍历数组 height 一次，计算能接的雨水总量还需要遍历一次。
• 空间复杂度：O(n)，其中 n 是数组 height 的长度。需要创建两个长度为 n 的数组 leftMax 和 rightMax。

9.*柱状图中最大的矩形

解法1：单调栈

class Solution {
public:
    //42.接雨水是找每个柱子左右两边第一个  大于  该柱子高度的柱子，
    //   而本题是找每个柱子左右两边第一个  小于  该柱子高度的柱子
    //故 单调栈中元素是 栈顶到栈底是单调递减（栈底元素最小）
    int largestRectangleArea(vector& heights) {
        //重点理解首尾加入两元素
        heights.insert(heights.begin(),0);    // 数组头部加入元素0
        heights.push_back(0);                 // 数组尾部加入元素0     
        int n=heights.size();     //此步必须放在前两步的下面，因为加入元素，使得size有变化
        stack stk;
        int ans=0;
        stk.push(0);
        for(int i=1;i

解法2：动态规划

class Solution {
public:
    int largestRectangleArea(vector& heights) {
        int n = heights.size();
        // 记录每个柱子 左边第一个小于该柱子的下标
        vector minLeftIndex(heights.size());
        minLeftIndex[0] = -1; // 注意这里初始化，防止下面while死循环
        for (int i = 1; i < n; i++) {
            int t = i - 1;
            // 这里不是用if，而是不断向左寻找的过程
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];

            minLeftIndex[i] = t;
        }
        // 记录每个柱子 右边第一个小于该柱子的下标
        vector minRightIndex(heights.size());
        minRightIndex[n - 1] = n; // 注意这里初始化，防止下面while死循环
        for (int i = n - 2; i >= 0; i--) {
            int t = i + 1;
            // 这里不是用if，而是不断向右寻找的过程
            while (t < n && heights[t] >= heights[i]) t=minRightIndex[t];
        
            minRightIndex[i] = t;  //记录下标
        }
        // 求和
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            ans = max(sum, ans);
        }
        return ans;
    }
};

10.*最大矩形

 解法1：单调栈+动态规划

class Solution {
public:
    int maximalRectangle(vector>& matrix) {
        int row=matrix.size(),col=matrix[0].size();
        if(row==0) return 0;
        //left[i][j] 为矩阵第 i 行第 j 列元素的左边连续 1 的数量
        vector> left(row,vector(col,0));
        //统计每一列的连续1的数量，即柱状图的高度
        for(int i=0;i up(row,0),down(row,0);
            stack stk;
            //求上边第一个小
            for(int i=0;i=left[i][j]){
                    stk.pop();
                }
                up[i]=stk.empty() ?-1:stk.top();
                stk.push(i);
            }
            //求下边第一个小
            stk=stack();  //栈清空
            for(int i=row-1;i>=0;--i){
                while(!stk.empty() && left[stk.top()][j]>=left[i][j]){
                    stk.pop();
                }
                down[i]=stk.empty() ?row:stk.top();   //注意这里栈为空，返回的是行数，而不是-1
                stk.push(i);
            }

            for(int i=0;i

• 时间复杂度：O(mn)，其中 m 和 n 分别是矩阵的行数和列数。计算 left 矩阵需要 O(mn) 的时间；对每一列应用柱状图算法需要 O(m) 的时间，一共需要 O(mn) 的时间。
• 空间复杂度：O(mn)，其中 m 和 n 分别是矩阵的行数和列数。我们分配了一个与给定矩阵等大的数组，用于存储每个元素的左边连续 1 的数量

 题型七：模拟

1.螺旋矩阵

 解法1：按层模拟

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        //考虑空矩阵
        if(matrix.size()==0||matrix[0].size()==0){   // 行 或 列 为0
            return {};
        }
        int rows=matrix.size(),cols=matrix[0].size();
        int left=0,right=cols-1,top=0,bottom=rows-1;
        vectorans;
        while(left<= right && top<= bottom){
              for(int col=left;col<= right;col++){
                    ans.push_back(matrix[top][col]); 
              }
              for(int row=top +1;row<= bottom;row++){
                    ans.push_back(matrix[row][right]); 
              }
              if(left<  right && top<  bottom){
                    for (int col = right -1 ; col >= left; col--) {
                         ans.push_back(matrix[bottom][col]); 
                    }
                    for (int row = bottom-1; row > top; row--) {
                         ans.push_back(matrix[row][left]); 
                    }
              }
              ++left;
              --right;
              ++top;
              --bottom;
        } 
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

• 空间复杂度：O(1)，除了返回的数组以外，空间复杂度是常数。

解法2：模拟

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        if(matrix.size()==0 || matrix[0].size()==0){
            return {};
        }
        vector> directions{{0,1},{1,0},{0,-1},{-1,0}};//右 下 左 上       
        int row=0,col=0,directionIdx=0;
        int rows=matrix.size(),cols=matrix[0].size();
        vector> visited(rows, vector(cols));  //判定是否被访问过
        vector ans(rows*cols);
        for(int i=0;i=rows || nextCol<0 || nextCol>=cols || visited[nextRow][nextCol]){
                directionIdx=(directionIdx+1)%4;
            }
            row+=directions[directionIdx][0];
            col+=directions[directionIdx][1];
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

• 空间复杂度：O(mn)，需要创建一个大小为 m×n 的矩阵 visited 记录每个位置是否被访问过。

2.螺旋矩阵II

 解法1：按层模拟

 思路：由外层向内层不断的填充矩阵，直到填入矩阵最内层的元素，每一层又按照上右下左的顺序填充。特别注意每次填充的首尾的边界。

class Solution {
public:
    vector> generateMatrix(int n) {
      vector>matrix(n,vector(n));
      int left=0,right=n-1,top=0,bottom=n-1;
      int num=1;
      while(left<= right && top<= bottom){
          for(int col=left;col<= right;col++){
              matrix[top][col]=num;
              num++;
          }
          for(int row=top +1;row<= bottom;row++){
              matrix[row][right]=num;
              num++;
          }

          if(left<  right && top<  bottom){ //满足此条件才可以：从右到左填入下侧元素，从下到上填入左侧元素
                for (int col = right -1 ; col >= left; col--) {
                    matrix[bottom][col] = num;
                    num++;
                }
                //前三步到头，最后一步在中间。  最后一步剩一个元素：这样免去讨论奇偶
                for (int row = bottom-1; row > top; row--) {      
                    matrix[row][left] = num;
                    num++;
                }
          }
          ++left;
          --right;
          ++top;
          --bottom;
        } 
        return matrix;     
    }
};

• 时间复杂度：O(n^2)，其中 n 是给定的正整数。矩阵的大小是 n×n，需要填入矩阵中的每个元素。

• 空间复杂度：O(1)，除了返回的矩阵以外，空间复杂度是常数。

 解法2：模拟

思路：初始位置设为矩阵的左上角，初始方向设为向右。若下一步的位置超出矩阵边界，或者是之前访问过的位置，或者下一个位置不为0，则顺时针旋转，进入下一个方向。

class Solution {
public:
    vector> generateMatrix(int n) {
        vector> matrix(n,vector(n));
        int row=0,col=0,num=1;
        //{0,1} 代表方向位置上 （行+0，列+1） 即向右
        vector> direction{{0,1},{1,0},{0,-1},{-1,0}};//右下左上
        int directionIdx=0;
        while(num <= n*n){
            matrix[row][col]=num;
            ++num;
            int nextRow=row+direction[directionIdx][0];
            int nextCol=col+direction[directionIdx][1];
            //若下一步的位置超出矩阵边界，或者是之前访问过的位置， 或者下一个位置不为0，则顺时针旋转，进入下一个方向
            if(nextRow<0 || nextRow>=n || nextCol<0 || nextCol>=n || matrix[nextRow][nextCol]!=0){
                directionIdx=(directionIdx+1)%4;  // 顺时针旋转至下一个方向
            }
            row+=direction[directionIdx][0];
            col+=direction[directionIdx][1];
        }
        return matrix;
    }
};

• 时间复杂度：O(n^2)，其中 n 是给定的正整数。矩阵的大小是 n×n，需要填入矩阵中的每个元素。

• 空间复杂度：O(1)，除了返回的矩阵以外，空间复杂度是常数。

3. #顺时针打印矩阵

 

与旋转矩阵完全相同

 解法1：按层模拟

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        //考虑空矩阵
        if(matrix.size()==0||matrix[0].size()==0){   // 行 或 列 为0
            return {};
        }
    int rows=matrix.size(),cols=matrix[0].size();
    int left=0,right=cols-1,top=0,bottom=rows-1;
    vectorans;
    while(left<= right && top<= bottom){
        for(int col=left;col<= right;col++){
              ans.push_back(matrix[top][col]); 
        }
        for(int row=top +1;row<= bottom;row++){
              ans.push_back(matrix[row][right]); 
        }
        if(left<  right && top<  bottom){
            for (int col = right -1 ; col >= left; col--) {
                    ans.push_back(matrix[bottom][col]); 
                }
            for (int row = bottom-1; row > top; row--) {
                    ans.push_back(matrix[row][left]); 
                }
        }
        ++left;
        --right;
        ++top;
        --bottom;
      } 
      return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

• 空间复杂度：O(1)，除了返回的数组以外，空间复杂度是常数。

解法2：模拟

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        if(matrix.size()==0 || matrix[0].size()==0){
            return {};
        }
        vector> directions{{0,1},{1,0},{0,-1},{-1,0}};       
        int row=0,col=0,directionIdx=0;
        int rows=matrix.size(),cols=matrix[0].size();
        vector> visited(rows, vector(cols));  //判定是否被访问过
        vector ans(rows*cols);
        for(int i=0;i=rows || nextCol<0 || nextCol>=cols || visited[nextRow][nextCol]){
                directionIdx=(directionIdx+1)%4;
            }
            row+=directions[directionIdx][0];
            col+=directions[directionIdx][1];
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

• 空间复杂度：O(mn)，需要创建一个大小为 m×n 的矩阵 visited 记录每个位置是否被访问过。 

4.*旋转图像

 解法1：使用辅助数组

思路：对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。代码对应于matrix_new[ j ][ (n-1)-i ]=matrix[ i ][ j ]

class Solution {
public:
    void rotate(vector>& matrix) {
        int n=matrix.size();
        auto matrix_new=matrix;  //值拷贝
        for(int i=0;i

• 时间复杂度：O(n^2)，其中 n 表示 matrix 的边长。

• 空间复杂度：O(n^2)，我们需要使用一个和 matrix 大小相同的辅助数组。 

解法2：用翻转代替旋转

class Solution {
public:
    void rotate(vector>& matrix) {
        int n=matrix.size();
        //1、水平翻转
        for(int i=0;i

• 时间复杂度：O(n^2)，其中 n 表示 matrix 的边长。

• 空间复杂度：O(1)，为原地翻转得到的原地旋转。 

5. 机器人能否返回原点

 解法1：模拟

class Solution {
public:
    bool judgeCircle(string moves) {
        int x=0,y=0;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 表示 moves 指令串的长度。我们只需要遍历一遍字符串即可。

• 空间复杂度：O(1)，我们只需要常数的空间来存放若干变量。

6.*下一个排列

 解法1：模拟

class Solution {
public:
    void nextPermutation(vector& nums) {
        for(int i=nums.size()-2;i>=0;--i){
            for(int j=nums.size()-1;j>i;--j){
                if(nums[i]

• 时间复杂度：O(n)，其中 n 表示 nums 字符串的长度。我们只需要遍历一遍字符串即可。

• 空间复杂度：O(1)，我们只需要常数的空间来存放若干变量。

7.*两数相加

 

解法1：模拟

 思路：由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };*/
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *prev = new ListNode();  // 定义新链表头部，用于返回结果
        ListNode *cur = prev;   // cur是可移动指针，用于指向存储两个数之和的位置
        int carry=0;           // 进位值初始化为0,每次相加之后计算carry,并用于下一位的计算
        while(l1 || l2){       // 直到计算到两链表最后一位
            // 如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个 0 
            carry += (l1==nullptr ?0: l1->val)+(l2==nullptr ?0: l2->val);

            /*将求和数赋值给新链表的节点，
              注意这个时候不能直接将sum赋值给cur->next = carry%10。这时候会报，类型不匹配。
              所以这个时候要创一个新的节点，将值赋予节点*/
            cur->next = new ListNode(carry%10);
            cur = cur->next;
            
            carry/=10;  //新的进位值

            l1 = l1!=nullptr ? l1->next : nullptr;
            l2 = l2!=nullptr ? l2->next : nullptr;   
        }
        //如果链表遍历结束后，有 carry>0，还需要在答案链表的后面附加一个节点，节点的值为 carry   
        if(carry > 0) cur->next = new ListNode(carry);
        return prev->next;
    }
};

• 时间复杂度：O(max⁡(m,n))，其中 m 和 n 分别为两个链表的长度。我们要遍历两个链表的全部位置，而处理每个位置只需要 O(1) 的时间。

• 空间复杂度：O(1)，注意返回值不计入空间复杂度。

8.*任务调度器

 解法1：模拟+哈希

class Solution {
public:
    int leastInterval(vector& tasks, int n) {
        unordered_map freq;
        for(char ch:tasks){
            ++freq[ch];    //将不同种类的任务出现的次数 放进哈希表中
        }
        int m=freq.size(); // 任务总数
        // nextValid​ 表示任务i因冷却限制，最早 可以执行的时间；
        // rest​ 表示任务i剩余执行次数。
        //初始时，所有的 nextValid​ 均为 1，而 rest​ 即为任务i在数组 tasks 中出现的次数。
        vector nextValid, rest;
        for (auto [_, v]: freq) {
            nextValid.push_back(1);
            rest.push_back(v);
        }

        //用 time 记录当前的时间
        //需要找到满足 nextValid≤time 的并且 rest​ 最大的索引 i
        int time = 0;
        for (int i = 0; i < tasks.size(); ++i) {
            ++time;
            int minNextValid = INT_MAX;
            for (int j = 0; j < m; ++j) {
                if (rest[j]) {
                    minNextValid = min(minNextValid, nextValid[j]);
                }
            }
            time = max(time, minNextValid);
            int best = -1;
            for (int j = 0; j < m; ++j) {
                if (rest[j] && nextValid[j] <= time) {
                    if (best == -1 || rest[j] > rest[best]) {
                        best = j;
                    }
                }
            }
            nextValid[best] = time + n + 1;
            --rest[best];
        }
        return time;
    }
};

• 时间复杂度：O(∣tasks∣⋅∣Σ∣)，其中 ∣Σ∣ 是数组 task 中出现任务的种类，在本题中任务用大写字母表示，因此 ∣Σ∣ 不会超过 26。在对 time 的更新进行优化后，每一次遍历中我们都可以安排一个任务，因此会进行 ∣tasks∣ 次遍历，每次遍历的时间复杂度为 O(∣Σ∣)，相乘即可得到总时间复杂度。

• 空间复杂度：O(∣Σ∣)。我们需要使用哈希表统计每种任务出现的次数，以及使用数组 nextValid 和 test 帮助我们进行遍历得到结果，这些数据结构的空间复杂度均为 O(∣Σ∣)。

9. #打印从1到最大的n位数

 解法1：模拟

class Solution {
public:
    vector printNumbers(int n) {      
        int N=(int)pow(10,n)-1;
        vector num(N);
        for(int i=0;i

• 时间复杂度：O(10^n)，生成长度为 10^n 的列表需使用 O(10^n) 时间。

• 空间复杂度：O(1)，建立列表需使用 O(1) 大小的额外空间（ 列表作为返回结果，不计入额外空间 ）。

10.数字1的个数

 解法1：数学规律（模拟）

 

 

当前位中 1 出现次数的计算方法：

(1)当 cur=0 时:此位 1 的出现次数只由高位 high 决定，计算公式为:high×digit

(2)当 cur=1 时:此位 1 的出现次数由高位 high 和低位 low 决定，计算公式为:high×digit+low+1

(3)当 cur=2,3,⋯ ,9 时:此位 1 的出现次数只由高位 high 决定，计算公式为:(high+1)×digit

class Solution {
public:
    int countDigitOne(int n) {
        int ans=0,high=n/10,cur=n%10,low=0;
        long digit=1; //digit 类型必须是 long
        while(high!=0 || cur!=0){
            if(cur==0){
                ans+=high*digit;
            }else if(cur==1){
                ans+=high*digit+low+1;
            }else{
                ans+=high*digit+digit;
            }
            //更新从个位到最高位的变量
            low+=cur*digit;
            cur=high%10;
            high=high/10;
            digit*=10;
        }
        return ans;
    }
};

• 时间复杂度：O(logn)，n 包含的数位个数与 n 呈对数关系。

• 空间复杂度：O(1)。

11.#1~n 整数中1出现的次数

 

 解法1：数学规律（模拟）

class Solution {
public:
    int countDigitOne(int n) {
        int ans=0,high=n/10,cur=n%10,low=0;
        long digit=1; //digit 类型必须是 long
        while(high!=0 || cur!=0){
            if(cur==0){
                ans+=high*digit;
            }else if(cur==1){
                ans+=high*digit+low+1;
            }else{
                ans+=high*digit+digit;
            }
            //更新从个位到最高位的变量
            low+=cur*digit;
            cur=high%10;
            high=high/10;
            digit*=10;
        }
        return ans;
    }
};

• 时间复杂度：O(logn)，n 包含的数位个数与 n 呈对数关系。

• 空间复杂度：O(1)。

12.第N位数字

解法1：数学规律（模拟）  

1. 确定所求数位的所在数字的位数

2. 确定所求数位所在的数字：所求数位在从数字 start 开始的第 [(n−1)/digit] 个 数字 中（ start 为第 0 个数字）。=>   num = start + (n - 1) / digit

3. 确定所求数位在 num 的哪一数位：所求数位为数字 num 的第 (n−1)%digit 位（ 数字的首个数位为第 0 位）。

class Solution {
public:
    int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { 
            n -= count;
            digit += 1;
            start *= 10;
            count = 9 * start * digit;
        }
        long num = start + (n - 1) / digit; 
        string s=to_string(num);
        return s[(n - 1) % digit] - '0'; 
    }
};

• 时间复杂度：O(logn)，所求数位 n 对应数字 num 的位数。digit 最大为 O(log⁡n) ；第一步最多循环 O(log⁡n) 次；第三步中将 num 转化为字符串使用 O(log⁡n) 时间；因此总体为 O(log⁡n) 。

• 空间复杂度：O(logn)，将数字 num 转化为字符串 str(num) ，占用 O(log⁡n) 的额外空间。

13.#数字序列中某一位的数字

解法1：数学规律（模拟）

class Solution {
public:
    int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { 
            n -= count;
            digit += 1;
            start *= 10;
            count = 9 * start * digit;
        }
        long num = start + (n - 1) / digit; 
        string s=to_string(num);
        return s[(n - 1) % digit] - '0'; 
    }
};

14. #圆圈中最后剩下的数字（约瑟夫环）

 解法1：数学+迭代

思路：输入 n,m，记此约瑟夫环问题为 「n,m 问题」 ，设解（即最后留下的数字）为 f(n)，则有：

「n,m问题」：数字环为 0,1,2,...,n−1，解为 f(n)；
「n−1,m问题」：数字环为 0,1,2,...,n−2，解为 f(n−1)；
  以此类推……

对于「n,m问题」，首轮删除环中第 m 个数字后，得到一个长度为 n−1 的数字环。由于有可能 m>n，因此删除的数字为 (m−1)%n，删除后的数字环从下个数字（即 m%n ）开始。

长度为 n 的序列最后一个删除的元素，应当是从 m % n 开始数的第 f(n-1,m)个元素。因此有 f(n, m) = (m % n + f(n-1,m)) % n = (m + f(n-1,m)) % n。

class Solution {
public:
    int lastRemaining(int n, int m) {
        int f=0;   // 无论 m 为何值，长度为 1 的数字环留下的是一定是数字 0
        for(int i=2;i<=n;++i){
            f=(f+m)%i;
        }
        return f;
    }
};

• 时间复杂度：O(n)，状态转移循环 n−1 次使用 O(n) 时间，状态转移方程计算使用 O(1) 时间；

• 空间复杂度：O(1)，只使用常数个变量。

15.@对角线遍历

 解法1：模拟

class Solution {
public:
    vector findDiagonalOrder(vector>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        vector res;
        for (int i = 0; i < m + n - 1; i++) {
            if (i % 2) {
                int x = i < n ? 0 : i - n + 1;
                int y = i < n ? i : n - 1;
                while (x < m && y >= 0) {
                    res.emplace_back(mat[x][y]);
                    x++;
                    y--;
                }
            } else {
                int x = i < m ? i : m - 1;
                int y = i < m ? 0 : i - m + 1;
                while (x >= 0 && y < n) {
                    res.emplace_back(mat[x][y]);
                    x--;
                    y++;
                }
            }
        }
        return res;
    }
};

• 时间复杂度：O(mn)，其中 m 为矩阵行的数量，n 为矩阵列的数量。需要遍历一遍矩阵中的所有元素，需要的时间复杂度为 O(mn)。

• 空间复杂度：O(1)，除返回值外不需要额外的空间。

解法2：ACM

#include
using namespace std;

vector> inputTwoMatrix(){
	string line, word;
	getline(cin, line);
	string subLine = line.substr(1, line.size() - 2);
	stringstream sin1(subLine);
	vector> map;
	int count = 0;
	while (getline(sin1, word, ']')) {
		string subWord;
		if (count == 0) {
			subWord = word.substr(1, word.size() - 1);
		}
		else {
			subWord = word.substr(2, word.size() - 2);
		}
		stringstream sin2(subWord);
		vector vec;
		while (getline(sin2, word, ',')) {
			vec.push_back(stoi(word));
		}
		map.push_back(vec);
		++count;
	}
	return map;
}

void printVecWithSpace(const vector& vec) {
	for (int i = 0; i != vec.size(); ++i) {
		cout << vec[i];
		if (i != vec.size() - 1) cout << " ";
	}
	cout << endl;
}

class Solution {
public:
	vector order(vector>& mat) {
		int m = mat.size();
		int n = mat[0].size();
		vector ans;
		for (int i = 0; i < m + n - 1; ++i) {
			if (i % 2) {
				int x = i < n ? 0 : i - n + 1;
				int y = i < n ? i : n - 1;
				while (x < m && y >= 0) {
					ans.emplace_back(mat[x][y]);
					x++;
					y--;
				}
			}
			else {
				int x = i < m ? i : m - 1;
				int y = i < m ? 0 : i - m + 1;
				while (x >= 0 && y < n) {
					ans.emplace_back(mat[x][y]);
					x--;
					y++;
				}
			}
		}
		return ans;
	}
};
int main() {
	
	vector> matrix = inputTwoMatrix();
	vector ret = Solution().order(matrix);
	printVecWithSpace(ret);

	system("pause");
	return 0;

}

16.整数转罗马数字

 解法1：模拟

const pair valueSymbols[] = {
    {1000, "M"},
    {900,  "CM"},
    {500,  "D"},
    {400,  "CD"},
    {100,  "C"},
    {90,   "XC"},
    {50,   "L"},
    {40,   "XL"},
    {10,   "X"},
    {9,    "IX"},
    {5,    "V"},
    {4,    "IV"},
    {1,    "I"},
};

class Solution {
public:
    string intToRoman(int num) {
        string roman;
        for (const auto &[value, symbol] : valueSymbols) {
            while (num >= value) {
                num -= value;
                roman += symbol;
            }
            if (num == 0) {
                break;
            }
        }
        return roman;
    }
};

 

题型八：十大排序

1.*课程表 （拓扑排序）

拓扑排序：给定一个包含 n 个节点的有向图 G，我们给出它的节点编号的一种排列，满足：

对于图 G 中的任意一条有向边 (u,v)，u 在排列中都出现在 v 的前面。

特点1：如果图 G 中存在环，那么图 G 不存在拓扑排序

特点2：如果图 G 是有向无环图，那么它的拓扑排序可能不止一种

解法1：深度优先搜索

思路：深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点

对于一个节点 u，如果它的所有相邻节点都已经搜索完成，那么在搜索回溯到 u 的时候，u 本身也会变成一个已经搜索完成的节点。相邻节点在栈中， u 在栈顶位置。

深度优先搜索：任取一个「未搜索」的节点开始进行深度优先搜索。

1、将当前搜索的节点 u 标记为「搜索中」，遍历该节点的每一个相邻节点 v：

    a.如果 v 为「未搜索」，那么我们开始搜索 v，待搜索完成回溯到 u；

    b.如果 v 为「搜索中」，那么我们就找到了图中的一个环，因此是不存在拓扑排序的；

    c.如果 v 为「已完成」，那么说明 v 已经在栈中了，而 u 还不在栈中，因此 u 无论何时入栈都不会影响到 (u,v) 之前的拓扑关系，以及不用进行任何操作。

2、当 u 的所有相邻节点都为「已完成」时，我们将 u 放入栈中，并将其标记为「已完成」

在整个深度优先搜索的过程结束后，如果我们没有找到图中的环，那么栈中存储这所有的 n 个节点，从栈顶到栈底的顺序即为一种拓扑排序。

优化：只需要判断是否存在一种拓扑排序，而栈的作用仅仅是存放最终的拓扑排序结果，因此我们可以只记录每个节点的状态，而省去对应的栈。

class Solution {
private:
    void dfs(int u){
        visited[u]=1;  //1 表示  搜索中
        for(int v:paths[u]){
            if(visited[v]==0){   //0表示  未搜索
                dfs(v);
                if(!flag)  return;
            }else if(visited[v]==1){
                flag=false;
                return;
            }
        }
        visited[u]=2;    //2表示  已完成
    }
    vector> paths;
    vector visited;
    bool flag=true;
public:
    bool canFinish(int numCourses, vector>& prerequisites) {
        paths.resize(numCourses);
        visited.resize(numCourses);
        for(const auto &pre:prerequisites){
            paths[pre[1]].push_back(pre[0]);
        }
        for(int i=0;i

class Solution {
private:
    bool DFS(int i, vector>& paths, vector& visited){
        if(visited[i]==2) return true;   // 当前访问节点已被其他节点启动的 DFS 访问，无需再重复搜索，直接返回 True
        if(visited[i]==1) return false;  // 在本轮 DFS 搜索中节点 i 被第 2 次访问，即 课程安排图有环 ，直接返回 False

        visited[i]=1;
        for(auto j:paths[i]){ // 递归访问当前节点 i 的所有邻接节点 j，当发现环直接返回 False
            if(!DFS(j, paths, visited)) return false;
        }
        // 当前节点所有邻接节点已被遍历，并没有发现环，则将当前节点 flag 置为 2 并返回 True
        visited[i]=2;
        return true;
    }   
public:
    bool canFinish(int numCourses, vector>& prerequisites) {
        vector> paths(numCourses);            // 确定行，列不确定
        vector visited(numCourses);                  // 用于判断节点是否已经被访问
        for(int i=0; i

• 时间复杂度：O(n+m)，其中 n 为课程数，m 为先修课程的要求数。这其实就是对图进行深度优先搜索的时间复杂度。

• 空间复杂度：O(n+m)，题目中是以列表形式给出的先修课程关系，为了对图进行深度优先搜索，我们需要存储成邻接表的形式，空间复杂度为 O(n+m)。在深度优先搜索的过程中，我们需要最多 O(n) 的栈空间（递归）进行深度优先搜索，因此总空间复杂度为 O(n+m)。

解法2：广度优先搜索

 思路：广度优先搜索：取出队首的节点 u：1、将 u 放入答案中

2、移除 u 的所有出边，也就是将 u 的所有相邻节点的入度减少 1。如果某个相邻节点 v 的入度变为 0，那么我们就将 v 放入队列中

class Solution {
private:
    vector> paths;
    vector visited;
public:
    bool canFinish(int numCourses, vector>& prerequisites) {
        paths.resize(numCourses);
        visited.resize(numCourses);
        for(const auto &pre:prerequisites){
            paths[pre[1]].push_back(pre[0]);
            ++visited[pre[0]];
        }

        queue q;
        for(int i=0;i

• 时间复杂度：O(n+m)，其中 n 为课程数，m 为先修课程的要求数。这其实就是对图进行广度优先搜索的时间复杂度。

• 空间复杂度：O(n+m)，题目中是以列表形式给出的先修课程关系，为了对图进行广度优先搜索，我们需要存储成邻接表的形式，空间复杂度为 O(n+m)。在广度优先搜索的过程中，我们需要最多 O(n) 的 队列 空间（迭代）进行广度优先搜索，因此总空间复杂度为 O(n+m)。

2.课程表II

 解法1：深度优先搜索

class Solution {
private:
    bool DFS(int i, vector>& paths,vector& visited){
        if(visited[i]==2) return true;
        if(visited[i]==1) return false;
        visited[i]=1;
        for(auto j:paths[i]){
            if(!DFS(j, paths, visited)) return false;
        }
        visited[i]=2;
        ans.push_back(i);
        return true;
    }
    vector ans;
public:
    vector findOrder(int numCourses, vector>& prerequisites) {
        vector> paths(numCourses);
        vector visited(numCourses);
        for(int i=0;i

3.课程顺序

解法1：深度优先搜索（拓扑）

class Solution {
private:
    bool DFS(int i, vector>& paths, vector& visited){
        if(visited[i]==2) return true;
        if(visited[i]==1) return false;
        visited[i]=1;
        for(const auto&j:paths[i]){
            if(!DFS(j, paths, visited)){
                return false;
            }
        }
        visited[i]=2;
        ans.push_back(i);
        return true;
    }
    vector ans;
public:
    vector findOrder(int numCourses, vector>& prerequisites) {
        vector> paths(numCourses);
        vector visited(numCourses);
        for(auto &pre:prerequisites){
            paths[pre[0]].push_back(pre[1]);
        }
        for(int i=0; i< numCourses; ++i){
            if(!DFS(i,paths,visited)) return {};
        }
        return ans;
    }
};

4.课程表IV

解法1：深度优先搜索（拓扑）

class Solution {
public:
    vector> visited;
    bool DFS(int u, int v, vector>& paths){
        if(visited[u][v]==2) return true;
        if(visited[u][v]==1) return false;
        for(auto &mid:paths[u]){    // 通过其他课程中转
            if(DFS(mid, v, paths)){
                visited[u][v]=2;
                return true;
            }
        }
        visited[u][v]=1;
        return false;
    }
public:
    vector checkIfPrerequisite(int numCourses, vector>& prerequisites, vector>& queries) {
        vector> paths(numCourses);
        visited = vector>(numCourses, vector(numCourses));
        
        for(const auto&pre:prerequisites){
            paths[pre[0]].push_back(pre[1]);
            visited[pre[0]][pre[1]]=2;
        }

        vector ans;
        for(auto &query:queries){
            ans.push_back(DFS(query[0], query[1], paths));
        }
        return ans;
    }
};

5.有向无环图中一个节点的所有祖先

 解法1：深度优先搜索（拓扑）

思路：（1） 从每个点i出发，寻找可以到达的其他点；
           （2）中间经过的点，点i即为其祖先节点；
           （3）注意遍历过程中，使用vis保证不重复访问，最后排序输出(已经排好序，不需要再排序)；

class Solution {
private:
    vector> paths;
    vector> ans;
    void DFS(int i, int u, vector& visited) {    
        for (const auto&v: paths[u]){
            if (!visited[v]){
                visited[v] = true;
                ans[v].push_back(i);
                DFS(i, v, visited);
            }
        }     
    }
public:
    vector> getAncestors(int n, vector>& edges) {
        paths = vector>(n);
        ans = vector>(n);
        for (auto &edge : edges){
            paths[edge[0]].push_back(edge[1]);
        }
        for (int i = 0; i < n; i++){
            vector visited(n);
            DFS(i, i, visited);
        }
        return ans;
    }
};

6.#将数组排成最小的数

 解法1：内置函数（sort排序）

class Solution {
public:
    string minNumber(vector& nums) {
        string ans;
        vector strs;
        for(int i=0;i

解法2：快排

class Solution {
public:
    string minNumber(vector& nums) {
        vector strs;
        for(int i = 0; i < nums.size(); i++)
            strs.push_back(to_string(nums[i]));
        quickSort(strs, 0, strs.size() - 1);
        string res;
        for(string s : strs)
            res.append(s);
        return res;
    }
private:
    void quickSort(vector& strs, int l, int r) {
        if(l >= r) return;
        int i = l, j = r;
        while(i < j) {
            while(strs[j] + strs[l] >= strs[l] + strs[j] && i < j) j--;
            while(strs[i] + strs[l] <= strs[l] + strs[i] && i < j) i++;
            swap(strs[i], strs[j]);
        }
        swap(strs[i], strs[l]);
        quickSort(strs, l, i - 1);
        quickSort(strs, i + 1, r);
    }
};

• 时间复杂度：O(nlogn)，n 为最终返回值的字符数量（ strs 列表的长度 ≤n ）；使用快排或内置函数的平均时间复杂度为 O(nlogn) ，最差为 O(n^2) 。

• 空间复杂度：O(n)，字符串列表 strs 占用线性大小的额外空间。

7.#数组中的逆序对

 解法1：归并排序

class Solution {
private:
    int mergeSort(vector& nums,vector& tmp,int left,int right){
        if(left>=right) return 0;
        int mid=left+(right-left)/2;
        int count=mergeSort(nums,tmp,left,mid)+mergeSort(nums,tmp,mid+1,right);
        int i=left,j=mid+1,pos=0;
        while(i<=mid && j<=right){
            if(nums[i]<=nums[j]){
                tmp[pos]=nums[i];
                i++;
                /*当前 lPtr 指向的数字比 rPtr 小，但是比 R 中 [0 ... rPtr - 1] 的其他数字大，
                  [0 ... rPtr - 1] 的其他数字本应当排在 lPtr 对应数字的左边，但是它排在了右边，
                  所以这里就贡献了 rPtr 个逆序对。*/
                count+=j-(mid+1);
            }else{
                tmp[pos]=nums[j];
                j++;
            }
            pos++;
        }

        for(int k=i;k<=mid;++k){ //右边遍历完事了   左边还剩呢
            tmp[pos++]=nums[k];
            count+=(j-(mid+1));
        }
        while(j<=right){ //左边遍历完事了   右边还剩了
            tmp[pos++]=nums[j++];
        }
        
        pos=0;
        while(left<=right){//将tmp中的元素  全部都copy到原数组里边去
            nums[left++]=tmp[pos++];
        }
        return count;
    }
public:
    int reversePairs(vector& nums) {
        vector tmp(nums.size());       
        return mergeSort(nums,tmp,0,nums.size()-1);
    }
};

• 时间复杂度：O(nlogn)，其中 n 为序列长度。

• 空间复杂度：O(n)，其中 n 为序列长度。因为归并排序需要用到一个临时数组。

8、排序数组

 解法1：快速排序

class Solution {
public:
    void quickSort(vector& nums,int low, int high){
        if(low& nums,int low, int high){
        int pivot=rand()%(high-low+1)+low;
        swap(nums[low], nums[pivot]);
        int temp= nums[low];
        while(low=temp)  high--;
            nums[low]=nums[high];
            while(low sortArray(vector& nums) {
        quickSort(nums,0,nums.size()-1);
        return nums;
    }
};

9、寻找第K大

解法1：快排

class Solution {
public:
    int partition(vector& nums,int low,int high){
        int pivot=rand()%(high-low+1)+low;
        swap(nums[pivot],nums[low]);
        int tmp=nums[low];
        
        while(low=tmp) low++;
            nums[high]=nums[low];
        }
        nums[low]=tmp;
        return low;
    }
    int quickSort(vector& nums,int low,int high,int K){
        //先进行一轮划分，p下标左边的都比它大，下标右边都比它小
        int index=partition(nums, low, high);
        //若p刚好是第K个点，则找到
        if(K==index-low+1){
            return nums[index];
        }else if(K a, int n, int K) {
        // write code here
        return quickSort(a, 0, n-1, K);
    }
};

题型九：位运算

1.根据数字二进制下 1 的数目排序

 解法1：暴力

class Solution {
private:
    //两个函数必须是static，不然会报错
    //计算n的二进制中 1 的数量
    static int get(int n){
        int count=0;
        while(n){
            count+=n%2;
            n/=2;
        }
        return count;
    }
    static bool cmp(int a,int b){
        int bitA=get(a);
        int bitB=get(b);
        if(bitA==bitB) return a sortByBits(vector& arr) {
        sort(arr.begin(),arr.end(),cmp);
        return arr;
    }
};

• 时间复杂度：O(nlogn)，其中 n 为整数数组 arr 的长度。

• 空间复杂度：O(n)，其中 n 为整数数组 arr 的长度。

2.*只出现一次的数字

位运算的异或运算 ⊕ 有以下三个性质：

1、任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a

2、任何数和其自身做异或运算，结果是 0，即 a⊕a=0

3、异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b

 解法1：位运算

class Solution {
public:
    int singleNumber(vector& nums) {
        int ans=0;
        for(const int&num:nums){   //等价于for(auto num:nums)
            ans ^= num;
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组长度。只需要对数组遍历一次。

• 空间复杂度：O(1)。

3.#数组中数字出现的次数

 解法1：分组异或

思路：如果我们可以把所有数字分成两组，使得：（1）两个只出现一次的数字在不同的组中；

（2）相同的数字会被分到相同的组中。那么对两个组分别进行异或操作，即可得到答案的两个数字。这是解决这个问题的关键。

记这两个只出现了一次的数字为 a 和 b，那么所有数字异或的结果就等于 a 和 b 异或的结果，我们记为 x。如果我们把 x 写成二进制的形式 ​，其中 xi∈{0,1}，xi=1 表示 ai​ 和 bi​ 不等，xi=0 表示 ai​ 和 bi​ 相等。假如我们任选一个不为 0 的 xi，按照第 i 位给原来的序列分组，如果该位为 0 就分到第一组，否则就分到第二组，这样就能满足以上两个条件。

class Solution {
public:
    vector singleNumbers(vector& nums) {
        //1、先对所有数字进行一次异或，得到两个出现一次的数字的异或值。
        int ans=0;
        for(int num:nums){
            ans^=num;
        }
        //2、在异或结果中找到任意为 1 的位。
        int one=1;
        while((one&ans)==0){
            one<<=1;  //相当于二进制左移1位
        }
        //3、根据这一位对所有的数字进行分组。在每个组内进行异或操作，得到两个数字。
        int a=0,b=0;
        for(int num:nums){
            if(one&num){
                a^=num;
            }else{
                b^=num;
            }
        }
        return vector{a,b};
    }
};

• 时间复杂度：O(n)，我们只需要遍历数组两次。

• 空间复杂度：O(1)，只需要常数的空间存放若干变量。

4.#数组中数字出现的次数II

解法1：位运算

class Solution {
public:
    int singleNumber(vector& nums) {
        vector counts(32); // 因为 int 最大到 2^31，所以二进制形式最大为 32 位
        for(int num:nums){
            for(int j=0;j<32;++j){
                counts[j]+=num&1;  // 更新第 j 位
                num>>=1;   // 第 j 位 --> 第 j + 1 位
            }
        }
        int ans=0,m=3;
        for(int i=0;i<32;++i){
            ans<<=1;  // 左移 1 位
            ans |= counts[31-i]%m; //当i为0时，counts[31]存的位加入res，最后移到最高位
        }
        return ans;
    }
};

• 时间复杂度：O(n)， 其中 n 位数组 nums 的长度；遍历数组占用 O(n) ，每轮中的常数个位运算操作占用 O(1) 。

• 空间复杂度：O(1)，数组 counts 长度恒为 32 ，占用常数大小的额外空间。

5.*比特位计数

解法1：Brian Kernighan 算法

 Brian Kernighan 算法的原理是：对于任意整数 x，令 x=x & (x−1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则  操作次数  即为 x 的「一比特数」。

class Solution {
private:
    int countOnes(int x){
        int ones=0;
        while(x>0){
            x=x&(x-1);
            ones++;
        }
        return ones;
    }
public:
    vector countBits(int n) {
        vector ans(n+1);
        for(int i=0;i<=n;++i){
            ans[i]=countOnes(i);
        }
        return ans;
    }
};

• 时间复杂度：O(nlog⁡n)，对于给定的 n，计算从 0 到 n 的每个整数的「一比特数」的时间都不会超过 O(log⁡n)。

• 空间复杂度：O(1)。

解法2：动态规划

思路：对于正整数 x，如果可以知道最大的正整数 y，使得 y≤x 且 y 是 2 的整数次幂，则 y 的二进制表示中只有最高位是 1，其余都是 0，此时称 y 为 x 的「最高有效位」。令 z=x−y，显然 0≤z

class Solution {     //动态规划——最高有效位
public:
    vector countBits(int n) {
        vector dp(n+1);
        int highBit=0;
        for(int i=1;i<=n;++i){
            //如果 i & (i−1)=0，则令 highBit=i，更新当前的最高有效位
            if ((i & (i - 1)) == 0) {   //&优先级低于==
                highBit = i;
            }
            dp[i] = dp[i - highBit] + 1;
        }
        return dp;
    }
};

• 时间复杂度：O(n) ， 对于每个整数，只需要 O(1) 的时间计算「一比特数」。

• 空间复杂度：O(1)。

6.*汉明距离

 解法1：Brian Kernighan 算法

Brian Kernighan 算法：记 f(x) 表示 x 和 x−1 进行与运算所得的结果（即 f(x)=x & (x−1)），那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。

class Solution {
public:
    int hammingDistance(int x, int y) {
        int s=x^y,ans=0;
        while(s){  //直到 s=0 为止
            s &= s-1;  //Brian Kernighan 算法优化：只遍历1，不遍历0
            ans++; //这样每循环一次，s 都会删去其二进制表示中最右侧的 1，最终循环的次数即为 s 的二进制表示中 1 的数量。
        }
        return ans;
    }
};

• 时间复杂度：O(log⁡C)，其中 C 是元素的数据范围，在本题中 log C=log 2^{31} = 31。

• 空间复杂度：O(1)。

解法2：位运算

class Solution {
public:
    int hammingDistance(int x, int y) {
        int s=x^y,ans=0;
        while(s){  //直到 s=0 为止
            ans+= s&1; //如果最低位为 1，那么令计数器加一
            s>>=1;
        }
        return ans;
    }
};

• 时间复杂度：O(log⁡C)，其中 C 是元素的数据范围，在本题中 log C=log 2^{31} = 31。

• 空间复杂度：O(1)。

解法3：内置函数

class Solution {
public:
    int hammingDistance(int x, int y) {
        return __builtin_popcount(x^y);  //先异或运算，再使用内置函数
    }
};

• 时间复杂度：O(1)。

• 空间复杂度：O(1)。

7.#二进制中1的个数 

  解法1：Brian Kernighan 算法

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int ans=0;
        while(n){
            n&=n-1;
            ans++;
        }
        return ans;
    }
};

• 时间复杂度：O(n)，需要求解的函数值有 n 个。

• 空间复杂度：O(n)，函数的递归深度为 n，需要使用 O(n) 的栈空间。

8.#求1+2+…+n

 解法1：递归

思路：使用逻辑运算符确定递归出口。以逻辑运算符 && 为例，对于 A && B 这个表达式，如果 A 表达式返回 False ，那么 A && B 已经确定为 False ，此时不会去执行表达式 B。我们可以将判断是否为递归的出口看作 A && B 表达式中的 A 部分，递归的主体函数看作 B 部分。如果不是递归出口，则返回 True，并继续执行表达式 B 的部分，否则递归结束。

class Solution {
public:
    int sumNums(int n) {
        //return n == 0 ? 0 : n + sumNums(n - 1);  无限制
         n && (n += sumNums(n-1));
         return n;
    }
};

• 时间复杂度：O(n)，递归函数递归 n 次，每次递归中计算时间复杂度为 O(1)，因此总时间复杂度为 O(n)。

• 空间复杂度：O(n)，递归函数的空间复杂度取决于递归调用栈的深度，这里递归函数调用栈深度为 O(n)，因此空间复杂度为 O(n)。

 9.#不用加减乘除做加法

 

解法1：位运算

class Solution {
public:
    int add(int a, int b) {
        //因为不允许用+号，所以求出异或部分和进位部分依然不能用+号，所以只能循环到没有进位为止
        while(b!=0){  // 当进位为 0 时跳出
            //c表示进位，a表示非进位
            int c=(unsigned int)(a&b)<<1; //C++中负数不支持左移位，因为结果是不定的
            a^=b;
            b=c;
        }
        return a;
    }
};

• 时间复杂度：O(1)，最差情况下（例如 a = 0x7fffffff ,b = 1 时），需循环 32 次，使用 O(1) 时间；每轮中的常数次位操作使用 O(1) 时间。

• 空间复杂度：O(1)，使用常数大小的额外空间。

10.最大单词长度乘积

解法1：位运算

class Solution {
public:
    int maxProduct(vector& words) {
        int n = words.size();
        vector masks(n);
        for (int i = 0; i < n; i++) {
            string word = words[i];
            for (int j = 0; j < word.size(); j++) {
                // 用数组 masks 记录每个单词的位掩码表示
                masks[i] |= ( 1 << (word[j] - 'a') );
            }
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // 判断第 i 个单词和第 j 个单词是否有公共字母
                if ((masks[i] & masks[j]) == 0) {
                    ans = max(ans, int(words[i].size() * words[j].size()));
                }
            }
        }
        return ans;
    }
};

• 时间复杂度：O(L + n^2)，其中 L 是数组 words 中的全部单词长度之和，n 是数组 words 的长度。预处理每个单词的位掩码需要遍历全部单词的全部字母，时间复杂度是 O(L)，然后需要使用两重循环遍历位掩码数组 masks 计算最大单词长度乘积，时间复杂度是 O(n^2)，因此总时间复杂度是 O(L + n^2)。

• 空间复杂度：O(n)，其中 n 是数组 words 的长度。需要创建长度为 n 的位掩码数组 masks。

题型十：并查集

1.*除法求值

题型十一：图论

题型十二：数论