算法——前缀和与差分

前缀和

1.一维前缀和

     前缀和相当于高中的数列求和，对于数列an来说，前n项的和即为Sn。
     有公式Sn=Sn-1+an。通常我们的下标从1开始，这是为了方便进行数据的处理。给定一个区间（l，r），求下标l到r的数据和，通常我们采用数组遍历的方法，这里如果用前缀和的话，就是直接Sr-Sl-1就可得出答案。

两者的时间复杂度为O（n）和O（1）。

下面先给出代码模板（源自Acwing）：

S[n]=S[n-1]+a[n];
a[l]+...+a[r]=S[r]-S[l-1];

具体代码：

#include
#include
using namespace std;
//一维前缀和
int a[10],s[10];
int sum(int l,int r)
{
    if(l>r) return 0;
    if(l==r) return a[r];
    return s[r]-s[l-1];     //l-1前一项
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        s[i]=s[i-1]+a[i];
    cout<<s[3]<<endl;   //前三项和
    cout<<sum(2,5); //区间2到5数的和
    system("pause");
    return 0;
}

2.二维前缀和

代码模板（源自Acwing）

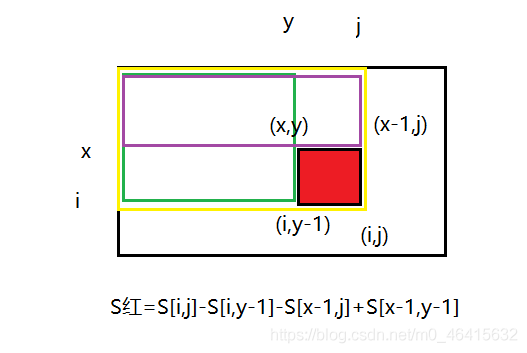
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1] ;
S[i,j]=S[i-1,j]+S[i,j-1]-S[i-1,j-1]+a[i,j];

先上图

这里的话，要是理解不了的话就用excel来理解 ，每行每列都是一个具体的数，而不是一条线，这样的话（i，y-1）（x-1,j）就很好理解了。

二位前缀和实例：

Acwing 99.激光炸弹
AC代码（关于边界那块看不太懂yxc大佬的讲解）

#include
using namespace std;
const int N=5000+10;    //区域的最大范围
int s[N][N];            //二维数组
int main()
{
    int n,r,x,y,w;
    scanf("%d%d",&n,&r);
    for(int i=1;i<=n;i++)
    {
        cin >> x >> y >> w;
        s[x+1][y+1]+=w;     //价值可以累加
    }
    for(int i=1;i<N;i++)
        for(int j=1;j<N;j++)
            s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+s[i][j];    //二维前缀和 i，j点的和
            
    int res=0;  //最大值
    if(r>=N) res=s[N][N];   //超过边界，最大值即为边界的
    for(int i=r;i<N;i++)
        for(int j=r;j<N;j++)
            res=max(res,s[i][j]-s[i-r][j]-s[i][j-r]+s[i-r][j-r]);   //从（r,r）开始遍历，
                                                                    //两点坐标为（i-r+1,j-r+1）(i,j) 二维前缀和公式
    
    cout << res;
    return 0;
        
}

差分

     读者熟悉等差数列：a1 a2 a3……an……，其中an+1= an + d（ n = 1,2,…n ）d为常数，称为公差， 即 d = an+1 -an , 这就是一个差分, 通常用D(an) = an+1- an来表示，于是有D(an)= d , 这是一个最简单形式的差分方程。

1.一维差分

首先给出差分的模板（源自Acwing）：

一维差分：给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c
二维差分：给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

     差分和前缀和相当于是一个逆运算的过程，下面来对差分进行具体的讲解。

首先我们给定一个数组 a：a[1],a[2],…a[n];
然后我们构建一个数组 b：b[1],b[2],…b[n];

使得b[i]=a[i]-a[i-1] 即 a[i]=b[1]+b[2]+…b[n];
容易看出，a是b的前缀和数组，这里我们把b叫做a的差分数组。

我们在构建差分数组时，往往使数组下标从1开始，这是因为让a[0]=0,b[1]=a[1]-a[0]，差分数组容易构建，且代码容易实现。

差分数组到底有什么用？

有这样一个例子，给定一个数组a，然后给定一个（l，r，c）操作序列，序列的意思是，在 [l,r] 这个区间内，实现相应的 c 操作，我们这里假设让l到r的区间内的数都加 c（其他操作类似）：
我们首先会想到暴力，直接遍历 l 到 r 区间，如果是m次，时间复杂度即为O（m*n）；但是这里我们就可以使用差分数组，时间复杂度则为O（1）。

要对 l 到 r 的 a 数组的数进行改变，我们可以通过改变 b 数组就可以实现，这是因为对 b[i] 的修改则会影响到 a[i] 之后的每一个数。

下面有这样两个操作：
在 b 数组中，让 b[l] + c ，而 a[l] 及其后开始的每一项都加上了一个c；
然后 b[r+1] - c,则 a[r+1]及其后开始的每一项都减去了一个c；

于是我们有结论：给区间[l, r]中的每个数加上c：

b[l] += c, b[r + 1] -= c

差分实例：Acwing 差分

AC代码：

#include
using namespace std;
const int N=1e5+10;
int a[N],b[N]; //前缀和数组a，差分数组b
/*void f(int l,int r,int c)
{
	b[l]+=c;
	b[r+1]-=c;
}
*/
int main()
{
    int n,m,l,r,c;
    cin>> n >> m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=n;i++)
        b[i]=a[i]-a[i-1];   //构建差分数组
    /*
    for(int i=1;i<=n;i++)	//另一种构建差分数组，只需要一个数组即可
    {
    	int x;
    	cin>>x;
    	f(i,i,x);
    }
    */
    while(m--)
    {
        cin>> l >> r >> c;
        b[l]+=c;            //关键操作
        b[r+1]-=c;
        //f(l,r,c);
    }
    
    for(int i=1;i<=n;i++)
    {
        a[i]=b[i]+a[i-1];
        cout<<a[i]<< ' ';
    }
    return 0;
}

2.二维差分

二维差分模板：

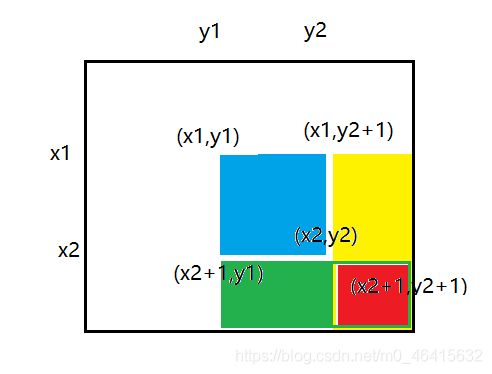
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

差分拓展成二维，即给二维数组的子矩阵每个元素加上c。
同理，有两个二维数组：a[ ][ ] 和 b[ ][ ]a是b的前缀和数组，b还是a的差分数组。
对b数组b[ i ][ j ]的修改，会影响a数组中a[ i ][ j ]及其之后的每个数。

进行如下的操作：

//等价于对a数组中从（x1,y1）到（x2,y2）每个数加c
void f(int x1,int y1,int x2,int y2,int c)
{
	b[x1][y1]+=c;	//x1,y1以后的每一个点+c
    b[x2+1][y1]-=c;	//绿色矩阵-c
    b[x1][y2+1]-=c;	//黄色矩阵-c
    b[x2+1][y2+1]+=c;	//红色被减了两次，再+c
}

//构建差分数组b
for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++)
		f(i,j,i,j,a[i][j]);

以上，欢迎大家指出其中的不足，相互交流。