PyTorch随笔 - Glow: Generative Flow with Invertible 1×1 Convolutions

欢迎关注我的CSDN：https://spike.blog.csdn.net/
本文地址：https://blog.csdn.net/caroline_wendy/article/details/129939225

论文：Glow - Generative Flow with Invertible 1×1 Convolutions

• 作者Kingma，来源于OpenAI，2018.7.10
• 最早的Flow Paper，承上启下

摘要：

Flow-based generative models (Dinh et al., 2014) are conceptually attractive due to tractability of the exact log-likelihood, tractability of exact latent-variable inference, and parallelizability of both training and synthesis.

• 基于流的生成模型（Dinh et al., 2014）在概念上具有吸引力，因为可以精确地计算对数似然值，可以精确地推断隐变量，而且训练和合成都可以并行化。

In this paper we propose Glow, a simple type of generative flow using an invertible 1 × 1 convolution.

• 在本文中，我们提出了一种简单的生成流类型，使用可逆的 1 × 1 卷积。

Using our method we demonstrate a significant improvement in log-likelihood on standard benchmarks.

• 使用我们的方法，我们在标准的基准测试上展示了对数似然值的显著提高。

Perhaps most strikingly, we demonstrate that a generative model optimized towards the plain log-likelihood objective is capable of efficient realisticlooking synthesis and manipulation of large images.

• 也许最引人注目的是，我们展示了一种优化了普通对数似然目标的生成模型，能够有效地合成和操作大型图像，并且看起来很真实。”

1x1卷积主要作用是通道融合。Flow-based Generative Models，基于流的生成模型。PDF，Probability Density Function，概率密度函数；CDF，Cumulative Distribution Function，累积分布函数

标准流，可见数据分布转换为标准分布。

概率密度函数：

输入 x -> log-det1(变换) -> z -> log-det2(变换) -> x，则 log-det1 + log-det2 = 0，即相反数的关系。

置换矩阵，行列式是0，三角矩阵（上三角或下三角都是0），对角线元素相乘，log就是对角线元素相加，即：

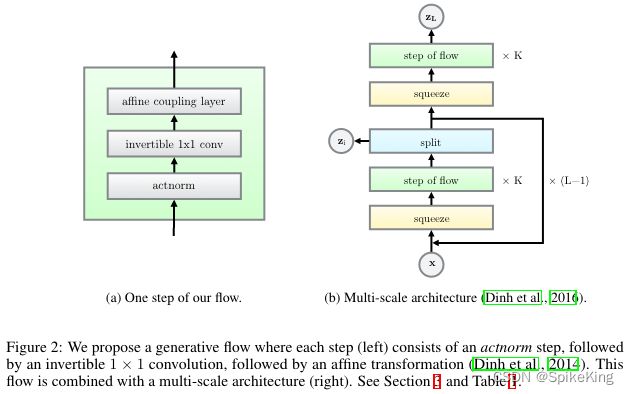
Multi-scale architecture，Flow：Actnorm、Invertible 1x1 Conv、Affine coupling layer

函数和逆函数，以及对数行列式（对数似然的增量），NN是非线性变换（神经网络），$\odot$ 表示element-wise操作，即Hadamard product

• x, y 都长度为c的向量

[x1, x2, x3] $\odot$ [w1, w2, w3] = [y1, y2, y3]，初始的y是服从标准分布。

Jacobi矩阵

[ w 1 0 0 0 w 2 0 0 0 w 3 ] \begin{bmatrix} w_{1} & 0 & 0\\ 0 & w_{2} & 0\\ 0 & 0 & w_{3}\\ \end{bmatrix} ​w1​00​0w2​0​00w3​​ ​

1x1的卷积操作，即一个点乘操作，一个矩阵操作。LU Decomposition(分解)，L是下三角矩阵，U是上三角矩阵，复杂度从$O(C^3)$降低为$O(C)$。

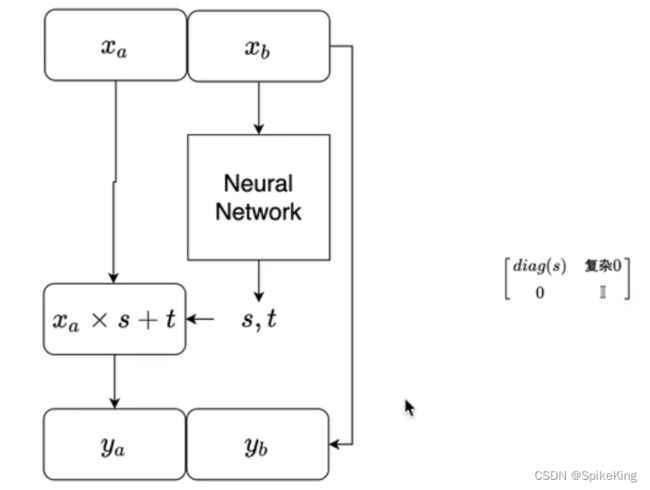
Affine Coupling Layer，仿射耦合层，Jacobi矩阵是分块矩阵，左上角和右上角有关。简易图如下：

关于Real NVP，即real-valued Non-Volume Preserving，实值非体积保持。

• Paper：Density Estimation using real NVP，来源于Google Brain

摘要：

Unsupervised learning of probabilistic models is a central yet challenging problem in machine learning. Specifically, designing models with tractable learning, sampling, inference and evaluation is crucial in solving this task. We extend the space of such models using real-valued non-volume preserving (real NVP) transformations, a set of powerful, stably invertible, and learnable transformations, resulting in an unsupervised learning algorithm with exact log-likelihood computation, exact and efficient sampling, exact and efficient inference of latent variables, and an interpretable latent space. We demonstrate its ability to model natural images on four datasets through sampling, log-likelihood evaluation, and latent variable manipulations.

• 无监督学习概率模型是机器学习中一个核心而又具有挑战性的问题。具体来说，设计具有可处理的学习、采样、推理和评估的模型是解决这一任务的关键。我们使用实值非体积保持（real NVP）变换，一种强大、稳定可逆、可学习的变换，扩展了这类模型的空间，从而得到了一种无监督学习算法，该算法可以精确地计算对数似然，精确而高效地进行采样，精确而高效地推断潜在变量，并且具有可解释的潜在空间。我们通过在四个数据集上进行采样、对数似然评估和潜在变量操作，展示了它对自然图像建模的能力。

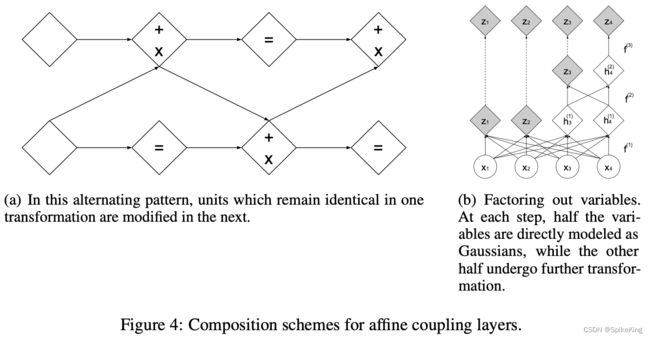
其中，Multi-scale architecture，$z_i$的相关计算，即：

Flow也可以引入条件生成。