关于时间复杂度O，T，Ω，θ以及它们的计算方法

时间复杂度有三种表示方法，分别是：T,O,θ

一.定义：

1.T
T就是程序需要执行的次数

for(int i=1;i<=n+2;i++)
   ans+=i;

T=n+2

2.O (程序时间上限------渐进时间复杂度)

设函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数c和n0，使得当n≥n0时，有f(n)≤cg(n)，则记做f(n) = O(g(n))

上面的例子如此枯燥无味，实际上就是把最高项系数化为1，其他项省略即可
（其他的上限，比如T=O（n），那么T=O(n^2)

比如还是上面那个例子，T=O(n)

且：
O(max(f(n),g(n)))=O(f(n))+O(g(n))
O(f)+O(g)=O(f+g)
O(f)O(g)=O(fg)

3.Ω (下限)
设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数 c和n0，使得当n≥n0时，有f(n)≥c g(n)，则记做f(n) = Ω (g(n))

其实就是和O的定义放过来了而已
还是上面那个例子，T=Ω (n)

4.θ（紧渐近界)
设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正常数c1，c2和n0，使得当n≥n0时，有c1 g(n)≤f(n)≤c2 g(n)，则记做f(n) = θ(g(n))

二.计算方法
有一类题类似T(n)=xxxxxxxx,问T(n)=???
这里不带递归类型的题目比较简单，不再赘述

1递归树

1.1 定义
递归树是迭代过程的一种图像表述。递归树往往被用于求解递归方程

//生成方法
初始：递归树只有根结点，其值为W(n)
不断继续下述过程：
将函数项叶结点的迭代式W(m)表示成二层子树
用该子树替换该页结点继续递归树的生成，直至树中无函数项（只有初值）为止。

那么时间复杂度就是每一层所有点的值的和（递归）

1.1 方法
这里用一个简单的例子说明：
令T(n)=T(n/4)+T(3n/4)+θ(n)
那么画图有：

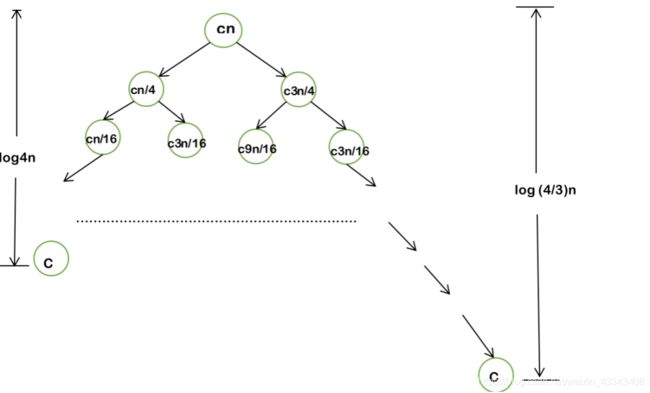
则，右半边层数比左半边层数少
则：
T(n) >= nlog4 n (假设只有左半边全满)
T(n) <= nlong(4/3)n (假设最大层全满)

那么T(n)=θ(nlog n)
（ps: 如果θ(n)变成O(n)，那么最后的结果也是O(nlogn)）

2.展开法
个人感觉这个方法比较麻烦，一般不太常用

其实这个方法就是递归树运用到了式子中

2.1 直接举个例子吧
T(n)=4T(n/2)+Θ(n)

解：
T(n)=2T(n/2)4^2T(n/2)+Θ(n)
       =2((n/2)^2+2T(n/4))+Θ(n)
       =2((n/2)^2+2(n/4)^2+……+2((n/2^i)^2+T(n/2^(I+1)))))+Θ(n)
可知当（n/2^(I+1)）=1时递归结束
则
T(n)=n^2(1/2+1/4+……)+Θ(n)
       =n^2+Θ(n)
       =Θ(n^2)
       =Ω(n^2)      

3.代入法（好评）
个人觉得最简单的方法
根据上述介绍的O，T，Ω，θ的定义，你可以直接设c1,c2等参数看是否可以满足条件
举个
T(n)=2T(n/4)+T(3n/4)+θ(nlogn),证明：T(n)=O(nlog^2n)

设T(n)<=c1nlog^2 n
  T(n)<=c1n/4 log^2(n/4)+c1(3n/4)log^2(3n/4)+dnlog(n)
  T(n)<=c1nlog^2n+(c1*1/2log(1/4)+c1*3/2*log(3/4)+d)nlogn+
  c1*(1/4log^2(1/4)+3/4*log^2(3/4))n
  (代入法的关键就是把它换成T(n)>=O(xxx)(你设的)+f(一个参数组成的表达式))
  只要有c1满足f>=0，那么这个设定就成立

4.总结
做题多了发现了一个规律：
T(n)=T()+T()+…T()+θ(f)
1）如果括号内数字✖️系数的和=n，那么就是f✖️logn
2） 如果括号内数字✖️系数的和>n,那么就是f✖️n
可以知道如果>n 每一层往下分别计算就相当于是等差数列求和
3）如果括号内数字✖️系数的和