二叉树的四种遍历 以及代码实现，看这一篇就够了

★ 前言：
二叉树的遍历，是我们数据结构 重点中的重点 ，90% 的笔试题都是二叉树遍历的变形
但是呢，有很多小伙伴对它的遍历方式还是有些模糊
那么，接下来我就为大家详细介绍各种遍历方式的区别：

何为 遍历 ：
就是把二叉树中的每个结点，一个不落的都走一遍。。

我们先封装一个 二叉树 的对象类：

public class TreeNode {
    int v;
    TreeNode left; // 左子树
    TreeNode right; // 右子树

    public TreeNode(int v) {
        this.v = v;
    }

    @Override
    public String toString() {
        return String.format("%c",v);
    }
}

1、DFS（Depth First Search）：深度优先遍历 – 栈

第一种视角看三种遍历：

（1）前序遍历：

遍历顺序：（递归）
把根结点放前面处理：

1、首先，处理 根结点
2、接着，完整地遍历根的 左子树（采用先序）
3、最后，完整地遍历根的 右子树（采用先序）

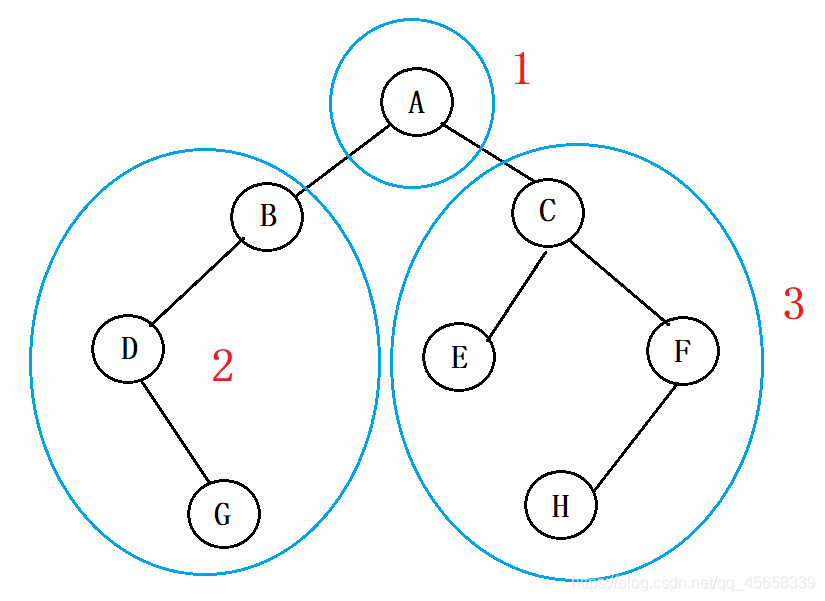
具体实现： 根 { 左子树 } { 右子树 }

① 我们是从 根结点 开始，
即 ： A{ } { }

② 由于我们是先遍历 左子树
所以， A { B{}{} } { }

A { B{ D{}{} }{} } { }

A { B{ D{}{G} }{} } { }

③ 最后遍历 右子树：

A { B{ D{}{G} }{} } { C{}{} }

A { B{ D{}{G} }{} } { C{E}{} }

A { B{ D{}{G} }{} } { C{E}{ F{}{} } }

A { B{ D{}{G} }{} } { C{E}{ F{H}{} } }

这样我们就得出了我们先序遍历出来的结果：
A B D G C E F H

① 代码实现：（递归）

// 前序遍历
    public static void preTraversal(TreeNode root) {
        // 前提：这颗树不是空树（根结点存在）
        if (root != null) {
            // 1、首先处理根结点
            System.out.printf("%c",root.v);
            // 2、按照前序的方式，递归处理该结点的左子树
            preTraversal(root.left);
            // 3、按照前序的方式，递归处理该结点的右子树
            preTraversal(root.right);
        } 
    }

② 代码实现：（非递归）

    public static void preOrder(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        while (!stack.isEmpty() || cur != null) {
            //遍历左子树
            while (cur != null) {
                System.out.println(cur.v);
                stack.push(cur);
                cur = cur.left;
            }
            //取出栈顶元素
            TreeNode top = stack.pop();
            //遍历右子树
            cur = top.right;
        }
    }

（2）中序遍历：

遍历顺序：（递归）
1、先遍历整颗树的 左子树（采用中序）
2、中间再处理 根结点 （根放到中间处理）
3、再遍历整棵树的 右子树 （采用中序）

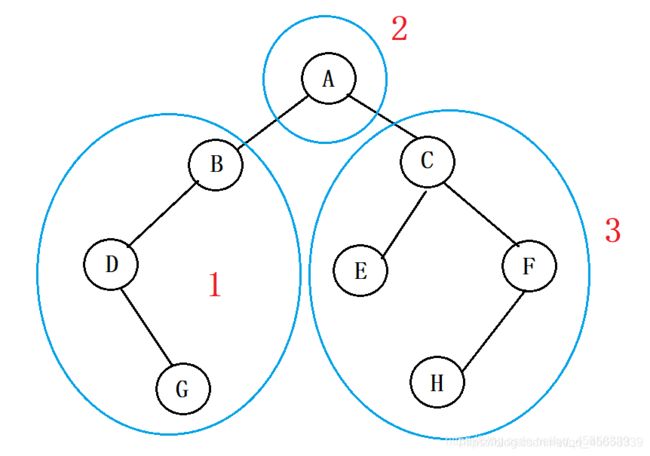
具体实现： { 左子树 } 根 { 右子树 }
即： { } A { }

我们先来遍历 左子树， 遍历的方式采用 中序遍历

{ {}B{} } A { }

{ { {}D{} }B{} } A { }

{ { {}D{G} }B{} } A { }

我们再来遍历 右子树，遍历的方式仍然采用 中序遍历

{ { {}D{G} }B{} } A { {}C{} }

{ { {}D{G} }B{} } A { {E}C{} }

{ { {}D{G} }B{} } A { {E}C{ {}F{} } }

{ { {}D{G} }B{} } A { {E}C{ {H}F{} } }

这样我们就得出了我们 中序遍历 出来的结果：
D G B A E C H F

① 代码实现：（递归）

// 中序遍历
    public static void inTraversal(TreeNode root) {
        if (root != null) {
            // 1、中序遍历左子树
            inTraversal(root.left);
            // 2、处理根
            System.out.printf("%c",root.v);
            // 3、中序遍历右子树
            inTraversal(root.right);
        }
    }

② 代码实现：（非递归）

public static void inOrder(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        while (!stack.isEmpty() || cur != null) {
            //遍历左子树
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            //取出栈顶元素
            TreeNode top = stack.pop();
            //回来的时候打印他
            System.out.println(top.v);
            //遍历右子树
            cur = top.right;
        }
    }

（3）后序遍历：

遍历顺序：（递归）
1、先遍历整颗树的 左子树（采用后序）
2、再遍历整棵树的 右子树 （采用后序）
3、最后再处理 根结点 （根放到最后处理）

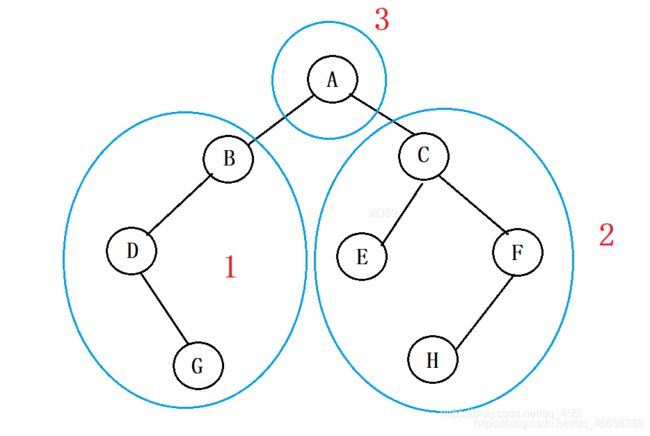
具体实现： { 左子树 } { 右子树 } 根
即： { } { } A

我们先来遍历 左子树， 遍历的方式采用 后序遍历：

{ {}{}B } { }A

{ { {}{}D }{}B } { }A

{ { {}{G}D }{}B } { }A

我们再来遍历 右子树，遍历的方式仍然采用 后序遍历

{ { {}{G}D }{}B } { }A

{ { {}{G}D }{}B } { {}{}C }A

{ { {}{G}D }{}B } { {E}{}C }A

{ { {}{G}D }{}B } { {E}{ {}{}F }C }A

{ { {}{G}D }{}B } { {E}{ {H}F}{}C }A

这样我们就得出了我们 后序遍历 出来的结果：
G D B E H F C A

① 代码实现：（递归）

// 后序遍历
    public static void postTraversal(TreeNode root) {
        if (root != null) {
            // 1、后续遍历左子树
            postTraversal(root.left);
            // 2、后续遍历右子树
            postTraversal(root.right);
            // 3、处理根
            System.out.printf("%c",root.v);

        }
    }

② 代码实现：（非递归）

    public static void postOrder(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        TreeNode last = null;//记录上次遍历的结点
        while (!stack.isEmpty() || cur != null) {
            //遍历左子树
            while (cur != null) {
                //第一次经过 cur 这个结点
                stack.push(cur);
                cur = cur.left;
            }
            //取出栈顶元素但不删除
            TreeNode top = stack.peek();
            if(top.right == null) {
                //第二次经过 top 这个结点（因为右边为空，所以可以看作第三次）
                //从左子树中回来，但是右子树为空，可以看作从右子树回来
                stack.pop();
                last = top;
                System.out.println(top.v);
            } else if (top.right == last){
                //第三次经过 top
                //说明从右子树中回来的
                stack.pop();
                last = top;
                System.out.println(top.v);
            } else {
                //第二次经过 top
                //说明从左子树中回来的
                cur = top.right;
            }
        }
    }

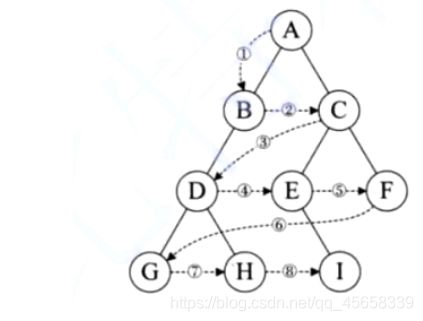
第二种视角看三种遍历：

前序 / 中序 / 后序，都是沿着红色的虚线前进

根据每次结点 经过的次数 来进行判断是 什么 类型 的遍历：

• 前序：A B D C E F
• 中序：D B A E C F
• 后序：D B E F C A

2、BFS（Broadcast First Search）：广度优先遍历

层次遍历： - - （队列）

按照从上到下，从左到右依次将二叉树遍历一遍

步骤：准备一个队列

1、启动阶段 : 把根节点放入队列

2、开启循环，直到队列为空（isEmpty）

• （1）从队列中取出队首结点
• （2）层序遍历经过该结点（打印）
• （3）把该结点的 左 / 右 孩子放入队列中（如果存在）

重复上述循环，即可层序遍历完二叉树

最终打印的结果是：A B C D E F G H I

代码实现：

//层序遍历
public class TreeLevelOrder {
    public static void levelOrderTraversal(TreeNode root) {
        if (root == null) {
            return;
        }
        //队列的元素的类型是树的结点
        Queue<TreeNode> queue = new LinkedList<>();
        //1、把根节点放入队列
        queue.add(root);
        //2、开启循环
        while (!queue.isEmpty()) {
            //（1）从队列中取出队首元素
            //node 就是层序遍历时经过的结点
            TreeNode node = queue.remove();
            //（2）打印遍历结点的值
            System.out.println(node.v);
            //（3）把该结点的左右子树放入队列中
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }
}

用途：（判断完全二叉树）