二叉树遍历之morris遍历
我们在遍历树时使用的 递归遍历 或者 迭代遍历,其实都是用到了堆栈来存储,增加了空间复杂度
有没有办法连这个空间都不要额外分配呢?
考虑一棵树:
1. 如果有 N 个节点,那么就有 2N 个指针(分别指向左子节点,右子节点)
2. 每一个节点,其实只有 1 个指针指向他,根节点没有节点指向,那么用到的指针个数:N-1
3. 结合1,2我们可以得知,还有 2N - (N - 1) = N + 1 个指针是空闲的
比如节点可能有 0,1,2个子节点,对应空闲指针 2,1,0 个
如果我们能够利用这些空闲指针,就可以降低额外的空间复杂度
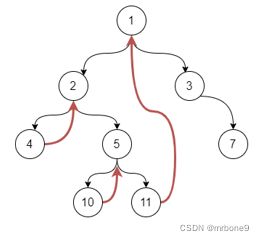
以前序遍历来看:1,2,4,5,10,11,3,7
以 节点 4 来讲
前缀节点:2
后缀节点:5
节点4 访问 节点5 需要回溯到其父节点 2;
节点10 访问 节点11 需要回溯到其父节点 5;
节点11 访问 节点3 需要回溯到其父节点 1;
当树的深度够大时,回溯的过程会很长,我们期望利用空闲指针,达成这样的效果
这种方式相当于利用空闲指针建立了一个索引,我们称之为 线索二叉树
前序方式的构建方式,称之为 前序线索二叉树,但是还存有一个问题:
我们方便的知道后缀节点,但是这样不容易知道 前缀节点是多少
后续方式比较复杂,用的最多的构建方式还是 中序线索二叉树
能够方便的得到前缀及后缀节点,我们来看看怎么做到的
其实中序遍历就是对每个节点的垂直投影
我们构建的线索是这样的:
前缀节点:当前节点的左子树最右的那个节点
比如 节点 1 的前缀节点,左子树 2 的最右节点 = 11
后缀节点:线索指针指向节点 或者原本右子树遍历到的最左节点
比如 节点 4 的后缀节点=2,节点 10 的后缀节点=5,节点 11 的后缀节点 = 1
我们在遍历时,构建的线索二叉树会破坏整个树的形态,所以在构建过程中,还会同时删除构建的线索,这样才能还原本来的样子。
中序线索二叉树 的构建过程:
1. 当前根节点如果为 NULL,直接返回
2.找当前节点的左子树的最右节点 // 节点 1
2.1 找到当前节点的 左子节点 // 节点 2
2.2 递归 左子节点的 右子节点,直到为NULL // 节点 11
2.3 将找到的该最右的子节点的 right 指向当前节点 // 节点 11->right = 节点 1
3. 继续构建,以 2 为 根节点,得到了 节点 4->right = 2
4. 以 2 为根节点的左子树完成,开始处理其右子树,同理,得到了 节点 10->right = 节点 5
5. 最后 节点 1 的整个左子树构建完成,开始处理其右子树
前序遍历:
void preorderMorris(struct TreeNode* cur)
{
if(cur == NULL)
return;
struct TreeNode *mostRight = NULL;
while(cur != NULL)
{
mostRight = cur->left;
if(mostRight != NULL)
{
while(mostRight->right != NULL && mostRight->right != cur) // 1
{
mostRight = mostRight->right;
}
if(mostRight->right == NULL) // 2
{
mostRight->right = cur;
printf("val=%d\n", cur->val);
cur = cur->left; // 3
continue;
}
else // 4
{
mostRight->right = NULL;
}
}
else
{
printf("val=%d\n", cur->val);
}
cur = cur->right; // 5
}
}1) 最右节点可能已经有构建,所以只有不为空并且不等于当前的根节点时才继续右子节点遍历
2)找到最右节点,指向当前根节点
3)继续根节点的余下左子节点构建过程
4)已经构建好了,我们需要删除该线索,维持原本树的形态。打印节点过程会在此前完成
5) 继续处理当前节点的右子树
中序遍历:框架不变,改变打印的地方
void inorderMorris(struct TreeNode* cur)
{
if(cur == NULL)
return;
struct TreeNode *mostRight = NULL;
while(cur != NULL)
{
mostRight = cur->left;
if(mostRight != NULL)
{
while(mostRight->right != NULL && mostRight->right != cur)
{
mostRight = mostRight->right;
}
if(mostRight->right == NULL)
{
mostRight->right = cur;
cur = cur->left;
continue;
}
else
{
mostRight->right = NULL;
printf("val=%d\n", cur->val);
}
}
else
{
printf("val=%d\n", cur->val);
}
cur = cur->right;
}
}后序遍历:框架不变,不同于前序,中序在构建中打印
一如既往的不走寻常路,我们需要观察下遍历顺序
1. 前缀节点刚好是左子节点时,打印然后删除索引,比如:4,10
2. 但是 11 不符合这个情况,是 1 的前缀节点,但不是其左子节点(2)
但是 11,5,2 的打印顺序正好是:以当前节点 1的左子节点开始的链 (2,5,11)的反序
3. 处理完左子树后,右子树节点 7 都不符合 1,2 条件,但是也是翻转即可
我们可以合并1,2的打印都作 翻转 (因为 1 个节点的翻转也是自己)
4. 翻转完成,记得再次翻转,否则树的这个链被反向了
struct TreeNode* reverse(struct TreeNode* head)
{
struct TreeNode *prev = NULL;
struct TreeNode *cur, *next;
cur = head;
while(cur != NULL)
{
next = cur->right;
cur->right = prev;
prev = cur;
cur = next;
}
return prev;
}
void printNode(struct TreeNode* head)
{
struct TreeNode* tail = reverse(head);
while(tail)
{
printf("val=%d\n", tail->val);
tail = tail->right;
}
reverse(tail);
}打印的时间就在删除索引的时刻
void postorderMorris(struct TreeNode* cur)
{
if(cur == NULL)
return;
struct TreeNode *root = cur; // last chain
struct TreeNode *mostRight = NULL;
while(cur != NULL)
{
mostRight = cur->left;
if(mostRight != NULL)
{
while(mostRight->right != NULL && mostRight->right != cur)
{
mostRight = mostRight->right;
}
if(mostRight->right == NULL)
{
mostRight->right = cur;
cur = cur->left;
continue;
}
else
{
mostRight->right = NULL;
printNode(cur->left);
}
}
cur = cur->right;
}
printNode(root);
}-------preorder Morris------
val=1
val=2
val=4
val=5
val=10
val=11
val=3
val=7
-------inorder Morris------
val=4
val=2
val=10
val=5
val=11
val=1
val=3
val=7
-------postorder Morris------
val=4
val=10
val=11
val=5
val=2
val=7
val=3
val=1
更多数据结构详解