leetcode python刷题记录（九）（81~90）

leetcode python刷题记录（九）（81~90）

81. 搜索旋转排序数组 II

class Solution:
    def search(self, nums: List[int], target: int) -> bool:

        left,right=0,len(nums)-1

        while left<=right:
            mid=(left+right)//2

            if nums[mid]==target:
                return True
            
            if nums[mid]>nums[left]: # 左半部分必然有序：
                if nums[left]<=target<nums[mid]: # 如果target在这个范围内，则舍弃右半部分
                    right=mid-1
                else: # 如果target不在这个范围内，舍弃左半部分
                    left=mid+1

            elif nums[mid]<nums[left]: # 右半部分必然有序
                if nums[mid]<target<=nums[right]:
                    left=mid+1
                else:
                    right=mid-1

            else:
                left=left+1

        return False  

82. 删除排序链表中的重复元素 II

class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        dummy=ListNode(0)
        dummy.next=head

        cur=dummy
        while cur.next and cur.next.next:
            if cur.next.val==cur.next.next.val:
                t=cur.next.val
                while cur.next and cur.next.val==t:
                    cur.next=cur.next.next
            else:
                cur=cur.next

        return dummy.next

83. 删除排序链表中的重复元素

class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:

        if head is None:
            return None
        
        cur=head

        while cur.next:
            if cur.val==cur.next.val:
                cur.next=cur.next.next
            else:
                cur=cur.next

        return head

84. 柱状图中最大的矩形

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n=len(heights)
        l,r=[0]*(n+1),[0]*(n+1)

        # 我们栈中元素存储的是下标，而对于两端的柱子，它们两侧的边界分别为-1和n。
        # 先从左往右循环，找到每个元素左边第一个比它矮的元素，并放入left数组。再从右往左循环，找到右边第一个比它矮的元素，并放入right数组
        st=[]
        for i in range(n):
            while len(st) and heights[st[-1]]>=heights[i]: # 维护一个单调递增的栈，元素如果比栈顶元素小则弹出栈顶元素，反复执行
                st.pop()
            if not len(st): # 栈为空则直接为左边界
                l[i]=-1
            else: # 不为空则此时栈顶元素即离heights[i]左边最近的小于它的值
                l[i]=st[-1]
            st.append(i)

        st=[]
        for i in range(n-1,-1,-1):
            while len(st) and heights[st[-1]]>=heights[i]:
                st.pop()
            if not len(st):
                r[i]=n
            else:
                r[i]=st[-1]
            st.append(i)

        res=0
        for i in range(n):
            res=max(res,heights[i]*(r[i]-l[i]-1))

        return res

85. 最大矩形

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        # 思路：先使用前缀和求出每一行每个位置连续1的个数
        # 之后参考84题的方法，用单调栈求出最大矩阵面积
        if not matrix:
            return 0
        
        m,n=len(matrix),len(matrix[0])
        pre=[0]*(n+1)
        res=0

        for i in range(m):
            # 前缀和
            for j in range(n):
                if matrix[i][j]=='1':
                    pre[j]=pre[j]+1
                else:
                    pre[j]=0

            # 单调栈
            stack=[-1]
            for k,num in enumerate(pre):
                while stack and pre[stack[-1]]>num:
                    index=stack.pop()
                    res=max(res,pre[index]*(k-stack[-1]-1))
                stack.append(k)

        return res

86. 分隔链表

class Solution:
    def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:
        
        p_head=p=ListNode(0)
        q_head=q=ListNode(0)

        cur=head

        while cur:
            if cur.val<x:
                p.next=cur
                p=p.next

            if cur.val>=x:
                q.next=cur
                q=q.next

            cur=cur.next

        q.next=None
        p.next=q_head.next

        return p_head.next

87. 扰乱字符串

参考：https://leetcode.cn/problems/scramble-string/solution/fu-xue-ming-zhu-ji-yi-hua-di-gui-by-fuxu-r98z/

class Solution:
    @functools.lru_cache(None) 
    # 可以把函数的输入和输出结果缓存住，在后续调用中如果遇到了相同的输入，直接从缓存里面读
    # 递归
    def isScramble(self, s1: str, s2: str) -> bool:
        if len(s1)==0:
            return True
        if len(s1)==1:
            return s1==s2
        if sorted(s1)!=sorted(s2):
            return False
        
        for i in range(1,len(s1)):
            if self.isScramble(s1[:i],s2[:i]) and self.isScramble(s1[i:],s2[i:]):
                return True
            if self.isScramble(s1[:i],s2[-i:]) and self.isScramble(s1[i:],s2[:-i]):
                return True
        
        return False

88. 合并两个有序数组

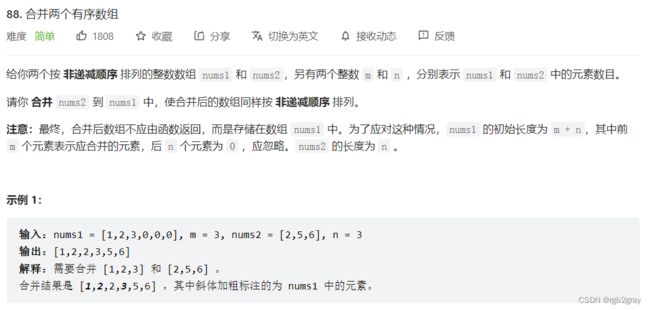
因为2个输入都是递增排列，所以倒着比大小，把大的放在最后即可

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        k=m+n-1

        while m>0 and n>0:
            if nums1[m-1]>nums2[n-1]:
                nums1[k]=nums1[m-1]
                m=m-1
            else:
                nums1[k]=nums2[n-1]
                n=n-1
            k=k-1
        # 当nums2比nums1长的时候，需要把nums2剩下的补到前面。nums1比nums2长的话则无需操作
        nums1[:n]=nums2[:n]

89. 格雷编码

class Solution:
    def grayCode(self, n: int) -> List[int]:
        if n==1:
            return [0,1]
        
        # 为得到第n个格雷编码，则需要将第n-1个编码作反转操作
        left=self.grayCode(n-1)
        right=left.copy() # 镜面对称
        right.reverse() # 反转
        right=[x+(1<<(n-1)) for x in right] #反转后首位补1

        return left+right

90. 子集 II

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:

        # 前面和78题一致，最后加了去重
        def dfs(step):
            if step==len(nums):
                res.append(path[:])
                return
            
            path.append(nums[step])
            dfs(step+1)
            path.pop()
            dfs(step+1)

        res=[]
        path=[]
        nums.sort()
        dfs(0)
        
        # 去重
        r=[]
        for x in res:
            if x not in r:
                r.append(x)

        return r