【CF1764C】Doremy‘s City Construction（二分图，贪心）

【题目描述】
有$n$个点，每个点的点权为$a_i$，你可以在任意两个点之间连边，最终连成的图需要满足：不存在任意的三个点，满足$a_u\le a_v\le a_w$（非降序）且边$(u,v)$和$(v,w)$存在。求最多能连的边数。

【输入格式】
第一行一个整数$t(1\le t\le 10^4)$，表示测试样例的数量。
对于每组测试样例第一行输入一个整数$n(2\le n\le 2\times 10^5)$，表示点的数量。
第二行输入$n$个整数$a_1,a_2,\dots ,a_n(1\le a_i\le 10^6)$，表示每个点的权值。
数据保证每组测试用例中的$n$的和不超过$2\times 10^5$。

【输出格式】
对于每组测试用例，输出一行共一个整数，即连出的图的最大边数。

【输入样例】

4
4
2 2 3 1
6
5 2 3 1 5 2
12
7 2 4 9 1 4 6 3 7 4 2 3
4
1000000 1000000 1000000 1000000

【输出样例】

3
9
35
2

【说明/提示】
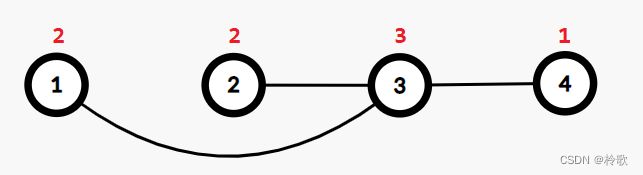
In the first test case, there can only be at most 3 edges in the graph. A possible construction is to connect $(1,3),(2,3),(3,4)$. In the picture below the red number above node $i$ is $a_i$.

The following list shows all such $u,v,w$ that the edges $(u,v)$ and $(v,w)$ exist.

• $u=1,v=3,w=2$
• $u=1,v=3,w=4$
• $u=2,v=3,w=1$
• $u=2,v=3,w=4$
• $u=4,v=3,w=1$
• $u=4,v=3,w=2$

【分析】

---

假如某个点与权值严格大于它的点相连，那么这个点就不能再连接权值小于等于它的点，反之同理。

那么我们考虑将所有点分成两个集合$S_1,S_2$，其中$S_1$中的所有点（数量为$c_1$）权值均小于等于该集合中的最大值$v_1$，$S_2$中的所有点（数量为$c_2$）权值均大于等于该集合中的最小值$v_2$，且$v_1<v_2$。那么$S_1$中的所有点均可以与$S_2$中的所有点相连，根据乘法原理可知边数为$c_1\ast c_2$。因此两个集合中点数乘积的最大值即为答案。

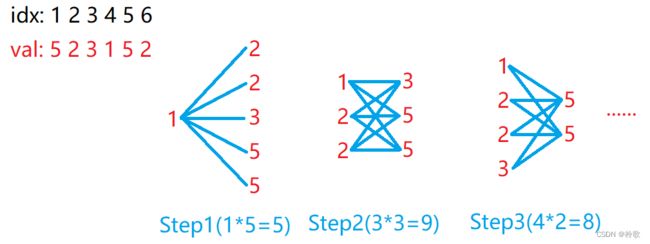
注意，如果每个点权值都相同最优解只能按下图这样连边，答案为$\lfloor n/2\rfloor$。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 200010;
int a[N];
int n;

int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n;
        for (int i = 0; i < n; i++) cin >> a[i];
        sort(a, a + n);
        if (a[0] == a[n - 1]) { cout << n / 2 << endl; continue; }
        LL res = 0;
        int idx = 0, cnt = 1;  // cnt表示较小数集合中的元素数量
        while (idx < n)
        {
            while (idx + 1 < n && a[idx + 1] == a[idx]) idx++, cnt++;
            res = max(res, LL(idx + 1) * (n - idx - 1));
            idx++, cnt++;
        }
        cout << res << endl;
    }
    return 0;
}