【C++】STL之stack、queue的使用和模拟实现+优先级队列（附仿函数）+容器适配器详解
之前的一段时间，我们共同学习了STL中一些容器，如string、vector和list等等。本章我们将步入新阶段的学习——容器适配器。本章将详解stack、queue的使用和模拟实现+优先级队列（附仿函数）+容器适配器等。
目录
（一）stack的使用和模拟实现
（1）stack的使用
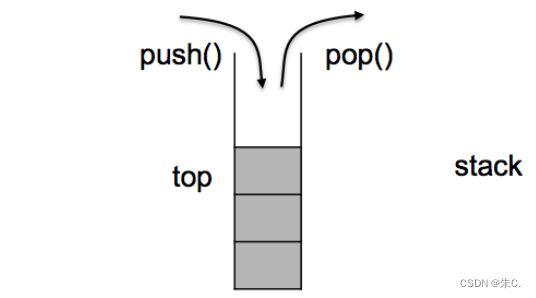
1、stack的介绍
2、stack的使用
（2）经典OJ题（最小栈、栈的弹出与压入序列、逆波兰表达式）
（3）stack的模拟实现
（二）queue的使用和模拟实现
（1）queue的使用
1、queue的介绍
2、queue的使用
（2）queue的模拟实现
（三）优先级队列（priority_queue）的使用、介绍和模拟实现
（1）优先级队列的介绍
（2）优先级队列的使用
（3）仿函数的介绍
（4）优先级队列的模拟实现
（四）容器适配器
（1）容器适配器的定义
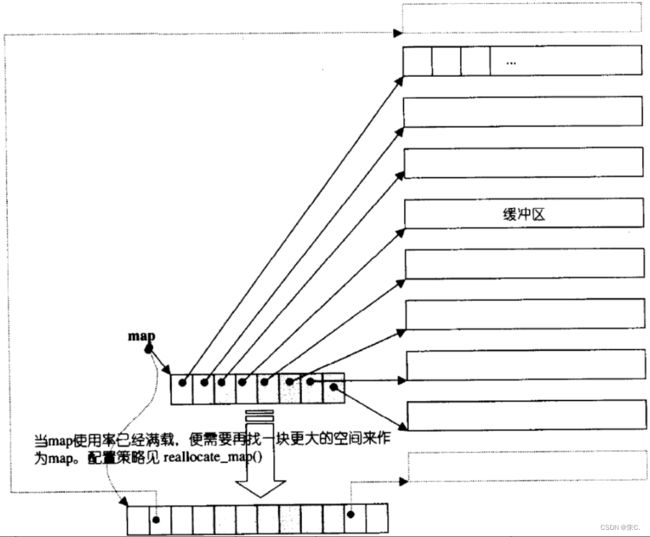
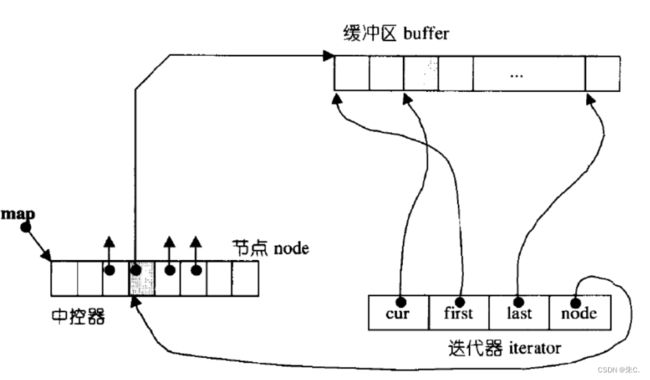
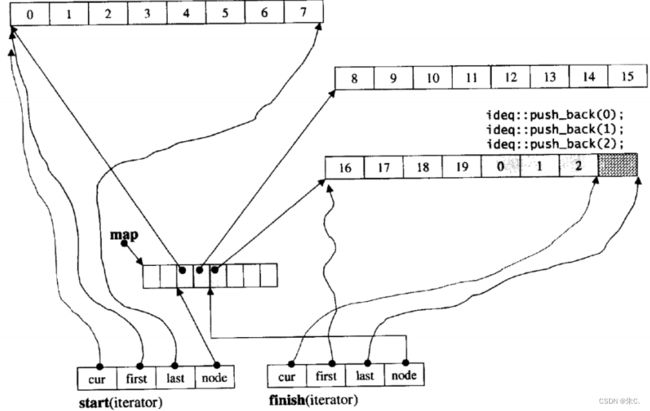
（2）stack、queue的底层架构——deque
（3）deque的介绍
（一）stack的使用和模拟实现
（1）stack的使用
1、stack的介绍
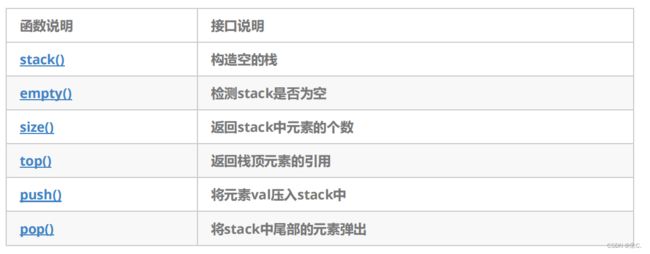
stack文档
stack文档
1. stack是一种容器适配器，专门用在具有后进先出操作的上下文环境中，其删除只能从容器的一端进行元素的插入与提取操作。
2. stack是作为容器适配器被实现的，容器适配器即是对特定类封装作为其底层的容器，并提供一组特定的成员函数来访问其元素，将特定类作为其底层的，元素特定容器的尾部(即栈顶)被压入和弹出。
3. stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类，这些容器类应该支持以下操作：
- empty：判空操作
- back：获取尾部元素操作
- push_back：尾部插入元素操作
- pop_back：尾部删除元素操作
4. 标准容器vector、deque、list均符合这些需求，默认情况下，如果没有为stack指定特定的底层容器，默认情况下使用deque（下文讲）。
2、stack的使用
我们查文档得：
其实这些操作我们在C语言数据结构中已经详细学过了，这里主要是复习一下。
操作大家都很熟悉啦，这里作者就浅浅演示一下如何历遍栈中的元素吧。
历遍栈中元素：
void test_stack()
{
std::stack> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
cout << endl;
}
输出为：4 3 2 1
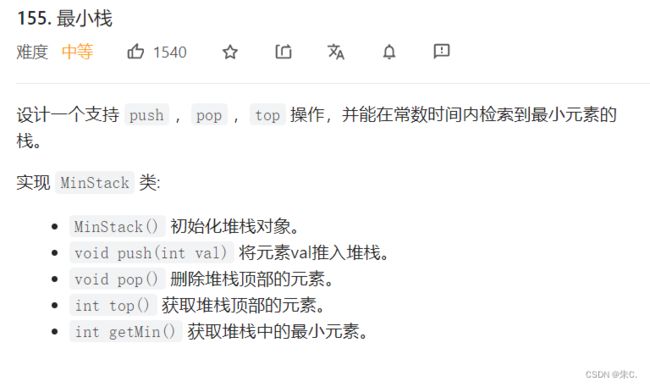
（2）经典OJ题（最小栈、栈的弹出与压入序列、逆波兰表达式）
力扣
https://leetcode.cn/problems/min-stack/
这道题我们要着重考虑的是如何获取栈中最小的元素。
思路：
- 设计两个栈，一个普通栈实现正常的插入删除操作，一个最小栈——为空时入一个数，后续栈中元素插入时比栈顶元素小的才可以进去最小栈，因为栈符合先进后出规则，这样操作后，最小栈的栈顶元素就是最小数。
- pop操作是如果普通栈栈顶元素和最小栈相同，则一起弹出，如果不同，普通栈弹出即可。
- top操作是直接获取普通栈栈顶元素即可。
代码：
class MinStack {
public:
MinStack() {
}
void push(int val) {
_st.push(val);
if(_minst.empty()||val<=_minst.top())
{
_minst.push(val);
}
}
void pop() {
if(_minst.top()==_st.top())
{_st.pop();
_minst.pop();
}
else
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack _st;
stack _minst;
};
===============================================================
栈的压入、弹出序列_牛客题霸_牛客网【牛客题霸】收集各企业高频校招笔面试题目，配有官方题解，在线进行百度阿里腾讯网易等互联网名企笔试面试模拟考试练习,和牛人一起讨论经典试题,全面提升你的技术能力https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
这和我们数据结构中的一类选择题很像。
思路为：
题目要我们判断两个序列是否符合入栈出栈的次序，我们就可以用一个栈来模拟。对于入栈序列，只要栈为空，序列肯定要依次入栈。那什么时候出来呢？自然是遇到一个元素等于当前的出栈序列的元素，那我们就放弃入栈，让它先出来。
写法：
我们创建一个栈，按照入栈顺序入，每次入栈时对比栈顶和出栈顺序是否一样，一样则弹出（出栈的序列往后加一），然后进行下一次循环比对。最后判断栈是否为空即可或者是否走到了出栈序列的末尾。
class Solution {
public:
bool IsPopOrder(vector pushV,vector popV) {
int pushi=0;
int popi=0;
stack st;
while(pushi ===============================================================
力扣https://leetcode.cn/problems/evaluate-reverse-polish-notation/
前言：我们平时的运算表达式都是中缀表达式，如：
中缀表达式我们人可以看懂，但机器不能，所以要设计一套机器能读懂的表达式，即逆波兰表达式，也称后缀表达式。
上面的中缀表示式转化成后缀表达式是2 1 + 3 *
转化流程如下：
我们有固定的一套逻辑：
- 遇到操作数，输出/存储
- 遇到操作符，跟栈顶操作符比较 a.栈为空或者比栈顶优先级高 – 入栈 b.比栈顶运算符优先级低或者一样 – 出栈顶操作符 -->然后跳到2、继续比较（依次再执行 a.b.）
- 后一个运算符来确定前一个运算符的优先级
- 最后将栈中操作符全部出栈
流程图：
那么逆波兰表达式怎么求值呢？
逆波兰表达式求值过程也相对固定，用到了我们的栈：
- 操作数，入栈
- 操作符，取连续两个栈顶数据运算，运算结果继续入栈，最后的结果就在栈里面
这道题的思路就是这样，代码如下：
class Solution {
public:
int evalRPN(vector& tokens) {
stack s1;
for(int i=0;i （3）stack的模拟实现
从栈的接口中可以看出，栈实际是一种特殊的 vector ，因此使用 vector 完全可以模拟实现 stack 。
代码如下：
amespace zc
{
template>
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
const T& top()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
（二）queue的使用和模拟实现
（1）queue的使用
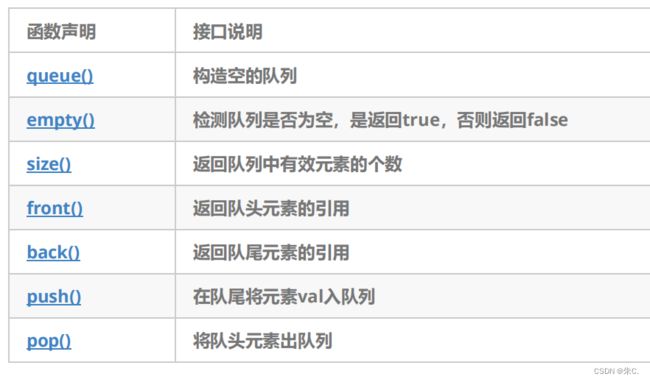
1、queue的介绍
1. 队列是一种容器适配器，专门用于在FIFO上下文(先进先出)中操作，其中从容器一端插入元素，另一端提取元素。
2. 队列作为容器适配器实现，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从队尾入队列，从队头出队列。
3. 底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
- empty：检测队列是否为空
- size：返回队列中有效元素的个数
- front：返回队头元素的引用
- back：返回队尾元素的引用
- push_back：在队列尾部入队列
- pop_front：在队列头部出队列
4. 标准容器类deque和list满足了这些要求。默认情况下，如果没有为queue实例化指定容器类，则使用标准容器deque。
2、queue的使用
我们查文档得：
这些接口的使用方法：
使用的代码：
void test_queue()
{
queue q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
//不支持迭代器了，因为栈让随便遍历是不好的
//后进先出不好保证，性质就无法维护了
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
输出的结果1 2 3 4（符合先进先出）
（2）queue的模拟实现
因为 queue 的接口中存在头删和尾插，因此使用 vector 来封装效率太低，故可以借助 list 来模拟实现 queue。
具体如下：
namespace zc
{
template>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
}; （三）优先级队列（priority_queue）的使用、介绍和模拟实现
（1）优先级队列的介绍
1. 优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。
2. 此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)。
3. 优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出，其称为优先队列的顶部。
4. 底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问，并支持以下操作：
- empty()：检测容器是否为空
- size()：返回容器中有效元素个数
- front()：返回容器中第一个元素的引用
- push_back()：在容器尾部插入元素
- pop_back()：删除容器尾部元素
5. 标准容器类vector和deque满足这些需求。默认情况下，如果没有为特定的priority_queue类实例化指定容器类，则使用vector。
6. 需要支持随机访问迭代器，以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作。
（2）优先级队列的使用
我们查文档可知：
优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。
注意：默认情况下priority_queue是大堆。
如果不熟悉堆的同学，可以回顾博主之前的博文——> 堆的详解
操作使用代码：
//底层是个堆（默认是个大堆） -- 底层用了vector
void test_priority_queue()
{
//greater库里写好了的仿函数
priority_queue, greater> pq;
pq.push(2);
pq.push(5);
pq.push(1);
pq.push(6);
pq.push(8);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
这里调用了greater的仿函数，所以是小堆。
运行结果：1 2 5 6 8
注意：
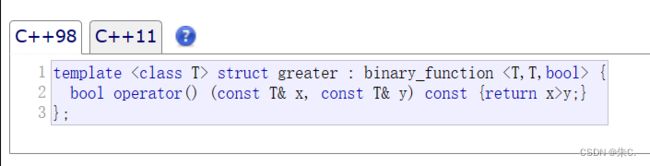
默认仿函数传的是less 仿函数，默认是大堆
- 优先级队列默认大的优先级高，传的是less仿函数，底层是一个大堆
- 想控制成小的优先级高，传greater仿函数，底层是一个小堆，这个是反过来的
- 算是设计的一个失误，但是我们没有质疑的能力，大家记住即可。
说到这里，什么是仿函数呢？？？这个模板参数的本质是什么呢？我们来进一步的探索：
（3）仿函数的介绍
仿函数 – 更高维度的泛型思想（不仅是数据类型的控制，更是逻辑的控制）
在使用仿函数之前，我们要包一下头文件#include< functional > 这个头文件
什么是仿函数：
看着像函数名，其实是个对象， 可以像调用函数一样去使用，实际上调用的是运算符重载。
我们以greater为例：
他是一个类，类中重载了()，所以可以像调用函数一样来调用这个类对象。
我们以sort函数为例：
这里就用到了仿函数（其实有点类似函数指针）
- 默认排的是升序 – 默认传的是less
- 我们还可以自己写仿函数，然后传过去
注意：
- 当我们要给一个顺序表排序的时候，当每个元素都是内置类型时，直接用库里的仿函数就可以
- 但是要排的元素是自定义类型的时候，就需要我们自己写一个仿函数了
例：
我们自定义一个日期类，这里要用到仿函数就必须我们呢自己重载>、<了：
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
friend ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
private:
int _year;
int _month;
int _day;
};
class PDateLess
{
public:
bool operator()(const Date* p1, const Date* p2)
{
return *p1 < *p2;
}
};
class PDateGreater
{
public:
bool operator()(const Date* p1, const Date* p2)
{
return *p1 > *p2;
}
};
void test_priority_queue2()
{// 大堆，需要用户在自定义类型中提供<的重载
priority_queue date;
date.push(Date(2023,4,1));
date.push(Date(2023, 4, 7));
date.push(Date(2023, 4, 2));
date.push(Date(2023, 4, 4));
while (!date.empty())
{
cout << date.top()<< " ";
date.pop();
}
cout << endl;
priority_queue,PDateGreater> date1;
date1.push(new Date(2023, 4, 1));
date1.push(new Date(2023, 4, 7));
date1.push(new Date(2023, 4, 2));
date1.push(new Date(2023, 4, 4));
cout << *(date1.top()) << endl;
} 补充：
- 只是一个普通类，重载了括号，可以像函数一样使用所以叫仿函数
- 是一个空类，只有一个字节
（4）优先级队列的模拟实现
其实主要就是堆的模拟实现的底层构想————>之前博主的博文：堆的模拟实现
主要是插入push的操作和弹出pop的操作的实现方法：
- push：我们把元素插入尾端，然后进行向上调整，也就是把它和它的父亲节点比较交换，直到找到资格核实的位置；
- pop：我们为了顺利把顶元素弹出，可以把顶部元素和末尾元素交换，然后弹出，然后再对交换上去的元素进行向下调整。
namespace zc
{
//仿函数/函数对象
template
struct less
{
bool operator()(const T& x,const T& y)
{
return x < y;
}
};
template
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
template,class Compare=less>
class priority_queue
{
public:
void adjust_up(int child)
{
int parent = (child - 1) / 2;
Compare com;
while (child>0)
{
if (com(_con[parent],_con[child]))
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down(int parent)
{
int child = parent * 2 + 1;
while (child < _con.size())
{
Compare com;
if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
{
child++;
}
if (com(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size()-1);
}
const T& top()
{
return _con[0];
}
size_t size()
{
return _con.size();
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
}; （四）容器适配器
（1）容器适配器的定义
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结)，该种模式是将一个类的接口转换成客户希望的另外一个接口。
其实stack、queue就是容器适配器，他将以前容器中存放的元素经过他的接口变成了有特殊作用的一组操作数据。
（2）stack、queue的底层架构——deque
虽然stack和queue中也可以存放元素，但在STL中并没有将其划分在容器的行列，而是将其称为容器适配器，这是因为stack和queue只是对其他容器的接口进行了包装，STL中stack和queue默认使用deque，比如：
（3）deque的介绍
deque(双端队列)：是一种双开口的"连续"空间的数据结构。
双开口的含义是：
可以在头尾两端进行插入和删除操作，且时间复杂度为O(1)，与vector比较，头插效率高，不需要搬移元素；与list比较，空间利用率比较高。
deque并不是真正连续的空间，而是由一段段连续的小空间拼接而成的，实际deque类似于一个动态的二维数组，其底层结构如下图所示：
双端队列底层是一段假象的连续空间，实际是分段连续的，为了维护其“整体连续”以及随机访问的假象，落在了deque的迭代器身上，因此deque的迭代器设计就比较复杂，如下图所示：
那deque是如何借助其迭代器维护其假想连续的结构呢？
deque的缺陷
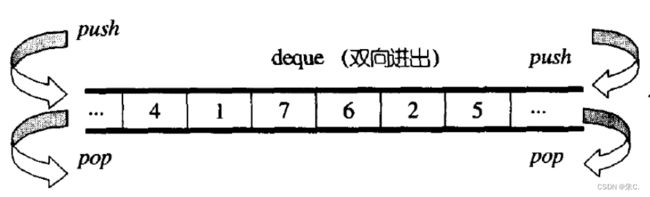
- 与vector比较，deque的优势是：头部插入和删除时，不需要搬移元素，效率特别高，而且在扩容时，也不需要搬移大量的元素，因此其效率是必vector高的。
- 与list比较，其底层是连续空间，空间利用率比较高，不需要存储额外字段。
但是，deque有一个 致命缺陷 ： 不适合遍历 ，因为在遍历时，deque的迭代器要频繁的去检测其是否移动到某段小空间的边界，导致效率低下，而序列式场景中，可能需要经常遍历，因此在实际中，需要线性结构时，大多数情况下优先考虑vector和list，deque的应用并不多，而目前能看到的一个应用就是，STL用其作为stack和queue的底层数据结构。
为什么选择deque作为stack和queue的底层默认容器？
stack是一种后进先出的特殊线性数据结构，因此只要具有push_back()和pop_back()操作的线性结构，都可 以作为stack的底层容器，比如vector和list都可以；queue是先进先出的特殊线性数据结构，只要具有 push_back和pop_front操作的线性结构，都可以作为queue的底层容器，比如list。但是STL中对stack和 queue默认选择deque作为其底层容器，主要是因为：
- 1. stack和queue不需要遍历(因此stack和queue没有迭代器)，只需要在固定的一端或者两端进行操作。
- 2. 在stack中元素增长时，deque比vector的效率高(扩容时不需要搬移大量数据)；queue中的元素增长 时，deque不仅效率高，而且内存使用率高。 结合了deque的优点，而完美的避开了其缺陷。
所以库中stack和queue的容器适配器接口是deque，而不是vector和list：
stack为例：
namespace zc
{
template>
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
const T& top()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};