《Rank-LIME: Local Model-Agnostic Feature Attribution for Learning to Rank》论文精读

一、论文信息

论文来源：https://arxiv.org/abs/2212.12722
原文下载：https://arxiv.org/pdf/2212.12722.pdf

摘要

Understanding why a model makes certain predictions is crucial when adapting it for real world decision making. LIME is a popular model-agnostic feature attribution method for the tasks of classification and regression. However, the task of learning to rank in information retrieval is more complex in comparison with either classification or regression. In this work, we extend LIME to propose Rank-LIME, a model-agnostic, local, post-hoc linear feature attribution method for the task of learning to rank that generates explanations for ranked lists. We employ novel correlation-based perturbations, differentiable ranking loss functions and introduce new metrics to evaluate ranking based additive feature attribution models. We compare Rank-LIME with a variety of competing systems, with models trained on the MS MARCO datasets and observe that Rank-LIME outperforms existing explanation algorithms in terms of Model Fidelity and Explain-NDCG. With this we propose one of the first algorithms to generate additive feature attributions for explaining ranked lists.

关键词：interpretability,post-hoc explanations model-agnostic interpretability, learning to rank, local explanations, LIME

二、要解决的问题

现有工作存在的问题

• 现有的解释方法对学习排名模型的解释少有研究。Singh and Anand扩展了 LIME 以解释⽂档与查询的相关性。但是，它们
  （i） 不评估⽣成的解释的质量
  （ii）不解释通过学习排名模型查询检索的⽂档生成的排序背后的原因。

• Singh等⼈提出了⼀种贪婪的⽅法来确定负责⽣成排名列表的top fearures（最相关的特征）。
  然⽽，他们的⽅法
  （i）只被建议⽤于以⼈⼯⼯程特征作为输⼊的rankers
  （ii）不能很好地扩展到⼤量特征。相⽐之下，论文作者认为⼀般的、事后排名解释技术（post-hoc ranking explanation techniques）对于理解深度学习排名模型（ learning-to-rank models）的⾏为具有巨⼤价值。

论文给出的方法（Rank-LIME）介绍

论文提出了Rank-LIME，这是⼀种为学习排名（ learning to rank）的任务⽣成与模型⽆关（model-agnostic）的局部（local）加性特征归因（ additive feature attributions）的⽅法。
给定⼀个架构未知的⿊盒排名器、⼀个查询、⼀组⽂档和解释特征，以及⼀⼩部分训练数据，Rank-LIME 返回⼀组最重要的特征的权重，测量这些特征对决定排名的相对贡献。我们专注于为最先进的基于transformer的排名器（例如BERT和T5）⽣成Rank-LIME解释，但Rank-LIME也可⽤于⽣成其他排名模型的解释。我们提出了基于Kendall’s Tau和NDCG的指标，以计算学习排名模型⽣成的解释的准确性，并将其与强基线进⾏⽐较。

贡献

论文的主要贡献是
（i）扩展LIME以解释List-Wise相关性函数，
（ii）引⼊基于相关性的实例扰动
（iii）在LIME中使⽤排名重建损失函数
（iv）提出评估排名特征属性的措施。
是最早使⽤特征归因解释列表相关性函数的作品之⼀。

三、前置知识

LIME

机器学习相对简单线性模型有更优异的效果，但是其复杂的原理让模型并不容易理解和解释。可解释的方法有很多种，大概可以分为全局解释和局部解释，以及与模型适配和与模型无关的方法,LIME是一种局部的、与模型无关的方法。

Lime（Local Interpretable Model-Agnostic Explanations）原理是使用训练的局部代理模型来对单个样本进行解释。假设对于需要解释的黑盒模型，取关注的实例样本，在其附近进行扰动生成新的样本点，并得到黑盒模型的预测值使用新的数据集训练可解释的模型（如线性回归、决策树），得到对黑盒模型良好的局部近似。

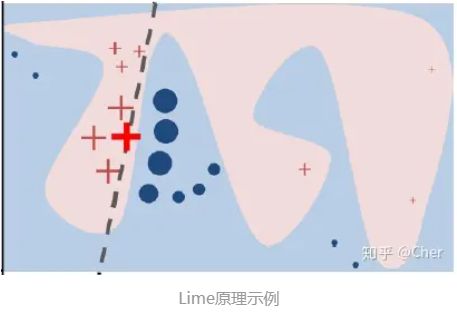
Local: 基于想要解释的预测值及其附近的样本，构建局部的线性模型或其他代理模型；
Interpretable: LIME 做出的解释易被人类理解。利用局部可解释的模型对黑盒模型的预测结果进行解释，构造局部样本特征和预测结果之间的关系；
Model-Agnostic: LIME 解释的算法与模型无关，无论是用 Random Forest、SVM 还是 XGBoost 等各种复杂的模型，得到的预测结果都能使用 LIME 方法来解释；
Explanations: LIME 是一种事后解释方法。

参考文章：https://zhuanlan.zhihu.com/p/193152643
黑盒模型事后归因解析：LIME 方法

Feature Attribution

归因方法主要是指输入特征的解释能力进行排名或度量，并以此来解释任务模型，有时也称为特征/变量重要性，相关性或影响力方法。大多数post-hoc都属此类，临床医生比较喜欢，因为有助于了解哪些功能可导致预期的结果，且能快速与自己的先验知识进行比较。我们可以根据解释产生机制将归因方法分为扰动和反向传播方法。基于反向传播的方法不是模型不可知的，因为它们通常是为特定的模型类设计的，或者要求模型的功能可区分。
参考文章：https://blog.csdn.net/weixin_38072029/article/details/117634867

Model-Agnostic

model agnostic指方法可以应用于任何模型，同时也是后验的（post hoc）。这种方法是分析输入和输出，而不能分析到模型内部。

参考文章：https://zhuanlan.zhihu.com/p/258988892

Local

模型无关的局部解释（Local Interpretable Model-Agnostic Explanations，LIME）指使用一个Interpretable Model拟合一个Uninterpretable Model的局部，比如使用Linear Model或者Decision Tree模拟Neural Network。

具体来讲，对于局部范围内的相同输入，我们希望两个模型的输出尽可能接近。这里要重点强调局部范围的概念，因为实际上Linear Model并不能模拟整个Neural Network但却可以模拟其中的一个Local Region，这也是LIME可行的原因。

参考文章：链接

Learning to Rank（LTR）

利用机器学习技术来对搜索结果进行排序，LTR的核心还是机器学习，只是目标不仅仅是简单的分类或者回归了，最主要的是产出文档的排序结果

步骤为：训练数据获取->特征提取->模型训练->测试数据预测->效果评估。

其中模型训练部分：
L2R算法主要包括三种类别：单文档方法（PointWise Approach），文档对方法（PairWise Approach)和文档列表方法（ListWise Approach)。

单文档方法（PointWise Approach）

单文档方法的处理对象是单独的一篇文档，将文档转换为特征向量后，机器学习系统根据从训练数据中学习到的分类或者回归函数对文档打分，打分结果即是搜索结果。下面我们用一个简单的例子说明这种方法。

下图是人工标注的训练集合，在这个例子中，我们对于每个文档采用了3个特征：査询与文档的Cosme相似性分值、査询词的Proximity值及页面的PageRank数值，而相关性判断是二元的，即要么相关要么不相关，当然，这里的相关性判断完全可以按照相关程度扩展为多元的，本例为了方便说明做了简化。

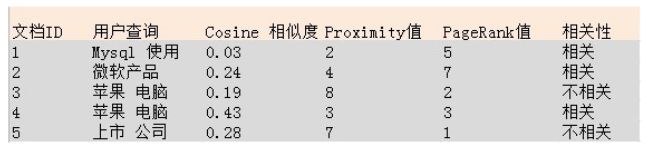
例子中提供了5个训练实例，每个训练实例分别标出来其对应的查询，3个特征的得分情况及相关性判断。对于机器学习系统来说，根据训练数据，需要如下的线性打分函数：

这个公式中，cs代表Cosine相似度变量，PM代表Proximity值变量，PR代表pageRank， 而a、b、c、d则是变量对应的参数。

如果得分大于设定阈值，则可以认为是相关的， 如果小于设定阈值则可以认为不相关。通过训练实例，可以获得最优的a、b、c、d参数组合，当这些参数确定后，机器学习系统就算学习完毕，之后即可利用这个打分函数进行相关性判断。对于某个新的查询Q和文档D，系统首先获得其文档D对应的3个特征值，之后利用学习到的参数组合计算两者得分，当得分大于设定的阈值，即可判断文档是相关文档，否则判断为不相关文档。

微软给定的数据如下在2.3节中给出了链接。
pointwise形式
– 输入：doc 的特征向量
– 输出：每个doc的相关性分数
– 损失函数: 回归loss，分类loss，有序分类loss

优点:
– 速度快，复杂度低.

缺点:
– 效果一般
– 没有考虑到文档之间的相对关系
– 在排序中，排在最前的几个文档对排序效果的影响非常重要，Pointwise没有考虑这方面的影响

pointwise常用算法

· Classification

Discriminative model for IR (SIGIR 2004)
McRank (NIPS 2007)

· Regression

Least Square Retrieval Function (TOIS 1989)
Regression Tree for Ordinal Class Prediction (Fundamenta Informaticae, 2000)
Subset Ranking using Regression (COLT 2006)

· Ordinal Classification

Pranking (NIPS 2002)
OAP-BPM (EMCL 2003)
Ranking with Large Margin Principles (NIPS 2002)
Constraint Ordinal Regression (ICML 2005)

文档对方法（PairWise Approach)

对于搜索任务来说，系统接收到用户查询后，返回相关文档列表，所以问题的关键是确定文档之间的先后相对顺序关系， 而Pairwise则将重点转向对文档关系是否合理的判断。

Pairwise主要是将排序问题转为了文档对顺序的判断。

对于查询Q1进行人工标注之后,Doc2=5的分数最高，其次是Doc3为4分，最差的是Doc1为3分，将此转为相对关系之后有:Doc2>Doc1、Doc2>Doc3、Doc3>Doc1，而根据这个顺序关系逆向也可以得到相关性的排序顺序，所以排序问题可以很自然的转为任意两个文档关系的判断,而任意两个文档顺序的判断就称为了一个很熟悉的分类问题.

Pairwise形式

输入：

排序函数给出文档对的计算得分

输出:

同一查询的一对文档
标注两个文档的相对关系，如果文档比更加相关，则
分别保留同一查询下的文档间关系

Pairwise常用算法:

Learning to Retrieve Information (SCC 1995)
Learning to Order Things (NIPS 1998)
Ranking SVM (ICANN 1999)
RankBoost (JMLR 2003)
LDM (SIGIR 2005)
RankNet (ICML 2005)
Frank (SIGIR 2007)
MHR(SIGIR 2007)
GBRank (SIGIR 2007)
QBRank (NIPS 2007)
MPRank (ICML 2007)
IRSVM (SIGIR 2006)
LambdaRank (NIPS 2006)
LambdaMART (inf.retr 2010)

虽然Pairwise方法对Pointwise方法做了改进，但是也明显存在两个问题:

1. 只考虑了两个文档的先后顺序，没有考虑文档出现在搜索列表中的位置

2. 不同的查询，其相关文档数量差异很大，转换为文档对之后，有的查询可能有几百对文档，有的可能只有几十个，最终对机器学习的效果评价造成困难。

文档列表方法（ListWise Approach)

与Pointwise和Pairwise不同，Listwise是将一个查询对应的所有搜索结果列表作为一个训练实例，因此也称为文档列方法。

文档列方法根据K个训练实例训练得到最优的评分函数F，对于一个新的查询，函数F对每一个文档进行打分，之后按照得分顺序高低排序，就是对应的搜索结果。所以关键问题是：拿到训练数据，如何才能训练得到最优的打分函数？

Listwise主要有两类:

• Measure specific: 损失函数与评估指标相关,比如:
  
• Non-measure specific:损失函数与评估指标不是显示相关,考虑了信息检索中的一些独特性
  这里介绍一种训练方法，它是基于搜索结果排列组合的概率分布情况来训练的，下图是这种方式训练过程的图解示意。
  

首先解释下什么是搜索结果排列组合的概率分布，我们知道，对于搜索引擎来说，用户输入査询Q， 搜索引擎返回搜索结果，我们假设搜索结果集合包含A. B 和C 3个文档，搜索引擎要对搜索结果排序，而这3个文档的顺序共有6种排列组合方式:

ABC, ACB, BAG, BCA, CAB和CBA,

而每种排列组合都是一种可能的搜索结果排序方法。

对于某个评分函数F来说，对3个搜索结果文档的相关性打分，得到3个不同的相关度得分F(A)、 F(B)和F©， 根据这3个得分就可以计算6种排列组合情况各自的概率值。不同的评分函数，其6种搜索结果排列组合的概率分布是不一样的。

了解了什么是搜索结果排列组合的概率分布，我们介绍如何根据训练实例找到最优的评分函数。上图展示了一个具体的训练实例，即査询Q1及其对应的3个文档的得分情况，这个得分是由人工打上去的，所以可以看做是标准答案。可以设想存在一个最优的评分函数g，对查询Q1来说，其打分结果是：A文档得6分，B文档得4分，C文档得3分， 因为得分是人工打的，所以具体这个函数g是怎样的我们不清楚，我们的任务就是找到一 个函数，使得函数对Q1的搜索结果打分顺序和人工打分顺序尽可能相同。既然人工打分 (虚拟的函数g) 已知，那么我们可以计算函数g对应的搜索结果排列组合概率分布，其具体分布情况如上图中间的概率分布所示。假设存在两个其他函数h和f，它们的计算方法已知，对应的对3个搜索结果的打分在图上可以看到，由打分结果也可以推出每个函数对应的搜索结果排列组合概率分布，那么h与f哪个与虚拟的最优评分函数g更接近呢？一般可以用两个分布概率之间的距离远近来度量相似性，KL距离就是一种衡量概率分布差异大小的计算工具，通过分别计算h与g的差异大小及f与g的差异大小，可以看出f比h更接近的最优函数g，那么在这个函数中，我们应该优先选f作为将来搜索可用的评分函数，训练过程就是在可能的函数中寻找最接近虚拟最优函数g的那个函数作为训练结果，将来作为在搜索时的评分函数。

上述例子只是描述了对于单个训练实例如何通过训练找到最优函数，事实上我们有K个训练实例，虽然如此，其训练过程与上述说明是类似的，可以认为存在一个虚拟的最优评分函数g (实际上是人工打分），训练过程就是在所有训练实例基础上，探寻所有可能的候选函数，从中选择那个KL距离最接近于函数g的，以此作为实际使用的评分函数。经验结果表明，基于文档列表方法的机器学习排序效果要好于前述两种方法。

Listwise常用算法:

· Measure-specific

AdaRank (SIGIR 2007)
SVM-MAP (SIGIR 2007)
SoftRank (LR4IR 2007)
RankGP (LR4IR 2007)
LambdaMART (inf.retr 2010)（也可以做Listwise）

· Non-measure specific

ListNet (ICML 2007)
ListMLE (ICML 2008)
BoltzRank (ICML 2009)

三种方法的对比

在工业界用的比较多的应该还是Pairwise，因为构建训练样本相对方便，并且复杂度也还可以。

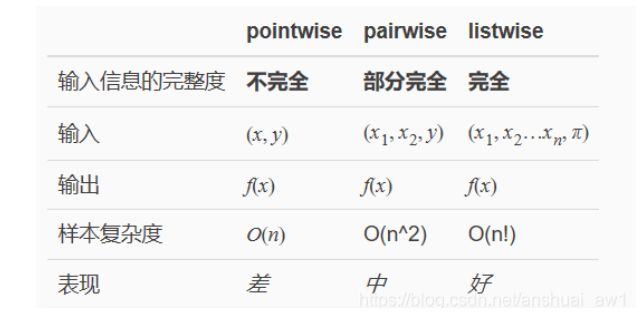
参考文章：【综述专栏】排序学习（Learning to rank）综述

post-hoc

事后(post-hoc)可解释性

指通过==开发可解释性技术解释已训练好的机器学习模型。==根据解释目标和解释对象的不同，post-hoc可解释性又可分为全局可解释性(global interpretability)和局部可解释性(local interpretability)。全局可解释性旨在帮助人们理解复杂模型背后的整体逻辑以及内部的工作机制，局部可解释性旨在帮助人们理解机器学习模型针对每一个输入样本的决策过程和决策依据。

post-hoc可解释性旨在利用解释方法或构建解释模型，解释学习模型的工作机制、决策行为和决策依据。

1. 全局解释

• 规则提取
  规则提取技术以难以理解的复杂模型或黑盒模型作为手点，利用可理解的规则集合生成可解释的符号描述，或从中提取可解释模型(如决策树、基于规则的模型等)，使之具有与原模型相当的决策能力。然而，规则提取方法提取的规则往往不够精确，因而只能提供近似解释，不一定能反映待解释模型的真实行为。

• 模型蒸馏
  当模型的结构过于复杂时，要想从整体上理解受训模型的决策逻辑通常是很困难的。解决该问题的一个有效途径是降低待解释模型的复杂度，而模型蒸馏(model distillation)则是降低模型复杂度的一个最典型的方法。然而，蒸馏模型只是对原始复杂模型的一种全局近似，它们之间始终存在差距。

• 激活最大化
  激活最大化方法思想较为简单，即通过寻找有界范数的输入模式，最大限度地激活给定的隐藏单元，而一个单元最大限度地响应的输入模式可能是 一个单元正在做什么的良好的一阶表示。激活最大化解释方法是一种模型相关的解释方法，相比规则提取解释和模型蒸馏解释，其解释结果更准确，更能反映待解释模型的真实行为。然而，激活最大化方法只能用于优化连续性数据，无法直接应用于诸如文本、图数据等离散型数据，故该方法难以直接用于解释自然语言处理模型和图神经网络模型。

2. 局部解释
   与全局可解释性不同，模型的局部可解释性以输入样本为导向，通常可以通过分析输入样本的每一维特征对模型最终决策结果的贡献来实现。经典的局部解释方法包括敏感性分析解释、局部近似解释、梯度反向传播解释、特征反演解释以及类激活映射解释等。

• 敏感性分析
  核心思想是通过逐一改变自变量的值来解释因变量受自变量变化影响大小的规律。敏感性分析作为一种模型局部解释方法，被用于分析待解释样本的每一维特征对模型最终分类结果的影响，以提供对某一个特定决策结果的解释。
  根据是否需要利用模型的梯度信息，敏感性分析方法可分为模型相关方法和模型无关方法。模型相关方法利用模型的局部梯度信息评估特征与决策结果的相关性。在模型无关敏感性分析方法中，待解释模型可以看作是黑盒，我们无需利用模型的梯度信息，只关注待解释样本特征值变化对模型最终决策结果的影响。
  敏感性分析方法提供的解释结果通常相对粗糙且难以理解。此外，敏感性分析方法无法解释特征之间的相关关系对最终决策结果的影响。

• 局部近似
  核心思想是利用结构简单的可解释模型拟合待解释模型针对某一输入实例的决策结果，然后基于解释模型对该决策结果进行解释。该解释方法实现简单，易于理解且不依赖待解释模型的具体结构，适于解释黑盒机器学习模型。但解释模型只是待解释模型的局部近似，因而只能捕获模型的局部特征，无法解释模型的整体决策行为。针对每一个输入实例，局部近似解释方法均需要重新训练一个解释模型来拟合待解释模型针对该实例的决策结果，因而此类方法的解释效率通常不高。此外，大多数的局部近似解释方法假设待解释实例的特征相互独立，因此无法解释特征之间的相关关系对决策结果的影响。

• 反向传播
  核心思想是利用DNN的反向传播机制将模型的决策重要性信号从模型的输出层神经元逐层传播到模型的输入以推导输入样本的特征重要性。然而，从理论上易知，如果预测函数在输入附近变得平坦,那么预测函数相对于输入的梯度在该输入附近将变得很小，进而导致无法利用梯度信息定位样本的决策特征。此外，梯度信息只能用于定位重要特征，而无法量化特征对决策结果的重要程度，利用基于重要性或相关性反向传播的解释方法则可以解决该问题。

• 特征反演
  尽管敏感性分析、局部近似以及梯度反向传播等方法在一定程度上可以提供对待解释模型决策结果的局部解释，但它们通常忽略了待解释模型的中间层，因而遗漏了大量的中间信息。而利用模型的中间层信息，我们能更容易地表征模型在正常工作条件下的决策行为，进而可提供更准确的解释结果。特征反演(feature inversion)作为一种可视化和理解DNN 中间特征表征的技术，可以充分利用模型的中间层信息，以提供对模型整体行为及模型决策结果的解释。特征反演解释方法可分为模型级(model-level) 解释方法和实例级(instance-level)解释方法。

参考文章：机器学习的可解释性（总结）

post-hoc linear feature attribution method

后验线性化特征归因⽅法不需要了解模型的内部结构，⽽是基于模型的输⼊和输出之间的关系来确定哪些特征对输出结果产⽣了显著的贡献。这些方法通常通过使用模型的输⼊和输出来拟合⼀个线性模型，然后使用该模型来计算每个输⼊特征的权重，从而确定其对输出结果的贡献。

四、论文中的方法介绍

论文提出了Rank-LIME，这是⼀种为学习排名（ learning to rank）的任务⽣成与模型⽆关（model-agnostic）的局部（local）加性特征归因（ additive feature attributions）的⽅法。
给定⼀个架构未知的⿊盒排名器、⼀个查询、⼀组⽂档和解释特征，以及⼀⼩部分训练数据，Rank-LIME 返回⼀组最重要的特征的权重，测量这些特征对决定排名的相对贡献。我们专注于为最先进的基于transformer的排名器（例如BERT和T5）⽣成Rank-LIME解释，但Rank-LIME也可⽤于⽣成其他排名模型的解释。我们提出了基于Kendall’s Tau和NDCG的指标，以计算学习排名模型⽣成的解释的准确性，并将其与强基线进⾏⽐较。

设 f 表示⼀个⿊盒学习排名模型，给定⼀个查询 q和⼀组⽂档 D ={d1,…,dN}，返回 D 中⽂档的排名 R，即 f (q，D) = R。排名模型 f 可以是单变量或多变量，使⽤逐点、成对或列表损失函数 [6] 进⾏训练。学习排名模型的主要⽅法是单变量评分函数，其中排名者分别对每个⽂档进⾏评分di∈D，然后根据其分数对⽂档进⾏排序。然⽽，由于我们的⽬标是解释⿊盒排名器，我们不对排名器做出任何假设，因此想要解释从⿊盒学习排名模型f 获得的排名 R。

查询对单个排名列表的学习排名模型⾏为的局部解释。具体来说，⽬标是为单个实例 = (, ) 解释从 (.) 获得的排名。解释模型通常在可解释（或简化）的输⼊ ′ 上⼯作，这些输⼊通过映射函数映射到原始输⼊

这⾥的Documents表示为⼀袋⽂字。对于 N 个单词的词汇表，每个document都由⼀个N维向量表示，其中第 i 个元素表示该⽂档中第 i个单词的频率

我们对 x ′ 周围的实例进⾏采样，以近似 f 的局部决策边界。扰动的实例⽤ z′ 表示。将受扰动的实例 z′ 馈送到排名器 f （hx （z′）），获得排名 Rz′ 。

我们将解释定义为模型 g ∈ G，其中 G 是线性模型的类，使得 然后通过最⼩化以下⽬标函数来获得 Rank-LIME 解释

Ω（g）：表示可解释模型的复杂性，
g : 对黑盒模型的解释定义为模型 g ∈ G，其中 G 是线性模型的类
f : f 表示⼀个⿊盒学习排名模型，给定⼀个查询 q和⼀组⽂档 D ={d1,…,dN}，返回 D 中⽂档的排名 R，即 f (q，D) = R
πx′：测量扰动实例的局部性。
：在LIME中，损失函数定义为均⽅误差，不适用于学习排名模型作为文档排名的输出。因此后面会讨论到损失、复杂性和局部性函数的选择。

让这个损失函数最小时的解释模型g即为最符合的解释模型

局部性函数

Δ（.）： 表示要解释的实例与解释特征空间中的扰动实例之间的距离函数，即 。我们将距离函数实例化为

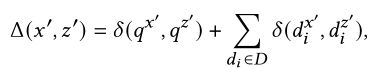
函数δ：根据解释特征测量查询或⽂档的向量表示之间的余弦距离
：方差

特征扰动

ΣC：来⾃训练数据集⼀部分特征的协⽅差矩阵，并将它们合并以在 Rank-LIME算法中⽣成扰动

原始 LIME 算法中的扰动是随机的。每个特征的采样都独⽴于以实例为中⼼的正态分布，µ= 0 且 σ = 1。然⽽，在 Rank-LIME中，我们在实例 x附近进⾏扰动，具有 µ = 0 和 Σ =ΣC 。这些包括单特征扰动和群扰动。

这有助于在扰动实例中保持训练集的特征相关
性，并避免噪声的流形外或分布外扰动。在存在⼤型⽂档和相关功能的情况下，这⼀点尤其重要。

损失函数

Rank-LIME 解释模型需要⼀个可微损失函数来量化两个排名列表之间的分歧，特别是原始排名 Rx 和扰动实例的排名 Rz。通常⽤于⽐较或评估排名列表的指标是 Kendall’s Tau和normalized discounted cumulative gain
(NDCG)。但是，这两个指标都不是可微的，因此不能⽤于训练回归模型以⽣成解释。因此，我们在 Rank-LIME 框架中使⽤上述不可微分指标的代理，如下所示：
ListNet： 表示每个具有概率分布的排名列表 – top-1 概率作为排列概率的近似值。然后，它使⽤交叉熵来衡量两个排名列表之间的差异。
RankNet：是⼀个成对概率损失函数，聚合以计算列表⽐较分数。
ApproxNDCG： 是 NDCG 的列表代理丢失，它⽤基于⽂档位置的平滑函数替换了 NDCG 的位置和截断功能。
NeuralNDCG： 是NDCG 的新代理，它使⽤NDCG 中排序函数的可微近似替代⽅法，然后将其插⼊ NDCG 公式以计算相关性。其神经排序功能能够以⾼精度和有限的错误率对⽂档进⾏排序。

五、实验与结果

数据集

我们将BM25，BERT 和T5排名器视为要解释的⿊盒排名器。微调后的BERT和T5排名器在先前的研究基础上使⽤MS MARCO passage排名数据集进⾏实验。为了进⾏实验，我们为数据集的测试集中的查询⽣成解释。我们根据每个排名者为⼗个最相关的⽂档列表⽣成解释。我们使⽤PyGaggle实现BM25，BERT和T5排名器。

不同扰动方法和损失函数比较

表 1：⽐较 Rank-LIME 的不同扰动⽅法（Perturbation）和损失函数（Loss Function），⽤于基于词的基于BERT 的排名器的解释。⽣成时间（Gen-Time）以秒为单位。

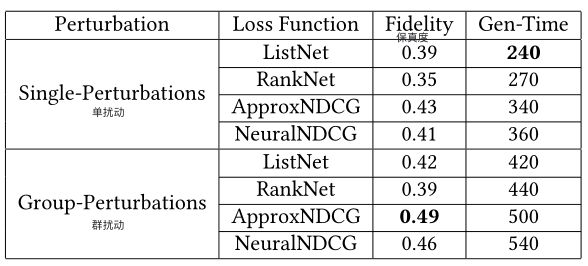
表1显示了当使⽤不同的扰动和损失函数时，基于BERT的rankers的基于词的解释中Rank-LIME的保真度。单扰动是指我们⼀次扰动单个特征值的扰动。群扰动是指我们⼀次扰动正在解释的实例中的特征组的扰动。我们发现ApproxNDCG 损失函数的性能⾄少优于其他⽤于⽣成 Rank-LIME 解释的列表式损失函数4.8%。在群扰动设置中，我们在每次扰动时屏蔽特征⼦集，其保真度⽐单个扰动场景⾼13.9%，但代价是⽣成时间（47%开销）。

评估指标

Model Faithfulness/Fidelity（模型忠实度/保真度）

评估解释模型在为给定查询重建⿊盒模型输出⽅⾯的效果。我们通过线性组合特征乘以其权重来构建解释模型的排名以形成排序。然后，我们计算⿊盒模型的排序和获得的排序之间的 Kendall’s Tau。

Explain-NDCG@10

Explain-NDCG@10还评估解释模型重建⿊盒模型输出的能⼒。与 Kendall’s Tau 不同，该指标对位置敏感，对于更好地解释排名靠前的⽂档的模型，可以获得更⾼的分数。我们使⽤学习排名模型（LTR model）获得的分数为每个⽂档分配NDCG 相关性。但是，⽂档的分数可能是负数，从⽽导致 NDCG 值不受限制。因此，我们对分数使⽤最小-最大归⼀化来决定相关性标签，同时保持统计显著性，正如Gienapp等⼈所建议的那样。分数越⾼，⽂档越相关。然后，我们使⽤这些相关性分数计算重建排名的 NDCG。我们会对所有查询的NDCG@10值求平均值，以报告此指标。

不同Competing Systems比较

竞争系统（Competing Systems）：指的是具有相同或者类似主要功能的工程系统，即具有相同或类似设计目的的工程系统。

表 2：⽐较不同竞争系统在基于模型保真度和 Explain-NDCG 的⽂本排名器基于词的解释⽅⾯的性能。

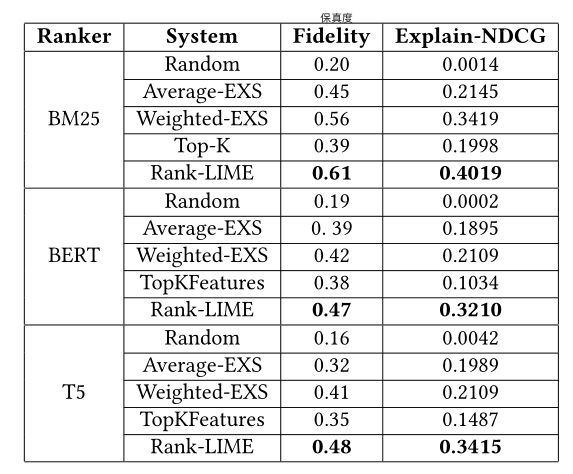
Rank-Lime与Competing systems：接下来，我们将Rank-LIME与表2中的竞争系统进⾏⽐较。报告的结果是从数据集的测试集中随机选择的 50 个实例中计算得出的。我们观察到加权EXS 的表现优于平均 EXS 24.4%。但是，Rank-LIME的表现⽐最佳基线⾼出11.9%。我们看到Rank-LIME在解释NDCG上的优势更⼤，⽐最强基线⾼出17.6%。与Kendall’s Tau（保真度）相⽐，Rank-LIME在Explain-NDCG上的更⼤优势直观地表明，与其他解释算法相⽐，Rank-LIME更注重解释⾼分⽂档。我们还观察到，与解释 BERT 排名器相⽐，解释算法在解释 BM25 排名器时的保真度提⾼了29.7%。这表明，与解释简单的排名模型相⽐，⽣成线性解释的基于 LIME 的算法在解释具有复杂决策边界的神经模型⽅⾯表现更差。

六、总结与Future Work

可解释性的概念以及我们如何量化它在很⼤程度上是主观的。然⽽，⾼度忠实和可解释的解释模型可以作为好的解释模型。在这项⼯作中，我们提出了⼀种与模型⽆关的算法，为学习排名任务中的结果提供线性特征归因。我们的⽅法是通⽤的，迎合 pointwise, pairwise, and listwise技术。我们提出了适合排名解释任务的新颖特征归因技术和评估指标，并表明我们的⽅法优于竞争基线。

未来的⼯作将在解释⽣成中纳⼊因果关系，⽽不是仅仅考虑相关性，因为相关性并不总是表明因果关系。通过⽤户研究，看看每个竞争系统的解释如何影响⼈类对⿊盒模型的理解也会很有趣。

---

以上内容仅代表本人对该论文的理解，仅供参考！
原论文阅读与下载：https://arxiv.org/pdf/2212.12722.pdf
个人批注版论文下载：https://download.csdn.net/download/GCTTTTTT/87685412（论文Rank-LIME: Local Model-Agnostic Feature Attribution for Learning to Rank的个人批注版本，涵盖对该论文的翻译、部分专有名词解释等内容）