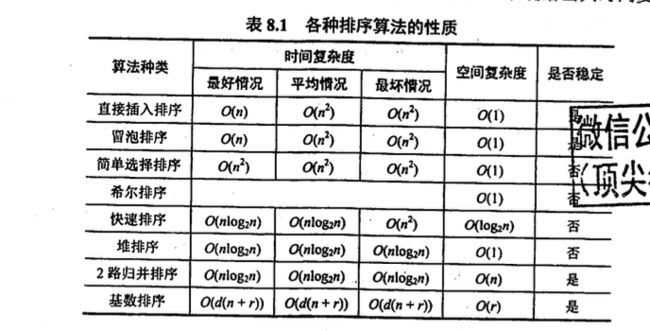
各种排序算法的思想和比较

对一个序列按关键字排列，使列表有序就是排序。
排序算法的稳定性：是指两个两个相同的元素，在排序之后，他两的相对位置是否会发生改变。

直接插入排序

算法思想：假设L[1~i-1]有序，将L[i]插入序列当中，使得该序列依然有序。
时间复杂度：最好情况 $O(n)$,最坏情况和平均情况$O(n^2)$
空间复杂度：$O(1)$
排序的趟数和序列的初始状态无关。
算法稳定。

折半插入排序

将直接插入排序中的查找过程换成了，二分查找。但是平均时间复杂度还是$O(n^2)$.

希尔排序

希尔排序是基于插入排序的改进。
算法思想：将待排序表分割成若干个形如L[i,i+d,i+2d,...,i+kd]的子表，然后分别对每个子表进行插入排序。
例如：

例如第一趟，划分成了[49,13],[38,27],[65,49],[97,55],[76,04],对于每一个子数组进行一个排序，在放入原来位置，结果就成了[13,27,49,55,04,49,38,65,97,76]。
**时间复杂度：**当n在某个特定的范围的时候，时间复杂度是$O(n^{1.3})$,最坏情况时间复杂度，$O(n^2)$
空间复杂度：$O(1)$
希尔排序是不稳定的排序算法。

冒泡排序

冒泡排序是基于交换排序的一种。
**算法思想：**从前往后或者从后往前两两相邻的互相比较，不符合要的排序规则，则交换，不断交换，将最小或者最大冒泡出去。
例如下面：

**时间复杂度：**最好情况$O(n)$,平均和最坏情况$O(n^2)$
注：冒泡排序每一趟排序之后都会将一个元素放置到最终位置上。
冒泡排序是一种稳定的算法。

快速排序

快速排序也是基于交换排序的一种。
算法思想：选择一个中枢（基准），和这个中枢进行比较，将比中枢大的和比中枢小的进行交换。然后递归的去排序左边区间的数，和右边区间的数。

在这里取第一个数为中枢，j指针往左找，找到第一个小于中枢的位置，和i位置交换，i指针往右找，找到第一个大于中枢的位置，交换到j的位置。以此类推。
**时间复杂度：**序列基本有序或者逆序的时候，时间复杂度最高$O(n^2)$,平均情况下时间复杂度$O(nlogn)$
空间复杂度：因为使用了递归，平均情况下$O(lo{g}_{2}n)$,最坏情况$O(n)$
快速排序算法是一种不稳定的算法。
注：在快速排序算法中，并不产生子序列，但每一趟排序后会将枢轴（基准）放在最终位置上。

选择排序

算法思想：每次从后面没有排序的数中选择一个最小的和当前数进行一个交换。
时间复杂度：$O(n^2)$
空间复杂度：$O(1)$
选择排序是一种不稳定的算法，例如：**2**,2,**1**经过一趟排序之后，第一个和第三个交换变成**1**,2,**2**。两个相同的2的相对位置明显发生了变化。

堆排序

大根堆，小跟堆，大根堆堆顶元素最大，小跟堆对顶元素最小。
是一颗完全二叉树，大根堆父节点大于所有子节点元素的值。
算法思想：先建堆，然后不断输出堆顶的元素，调整堆。
建大根堆的过程：

1. 将数组序列写成二叉树的形式
2. 从n/2向下取整的非终端结点开始调整，[n/2]之前是非终端结点，后面是叶子结点。
3. 将父节点和左右孩子更大的那个进行交换。从[n/2]到0的顺序依次调整。
4. 重复3,就可以得到一个大根堆。

例如：建成的堆87,45,78,32,17,65,53,09

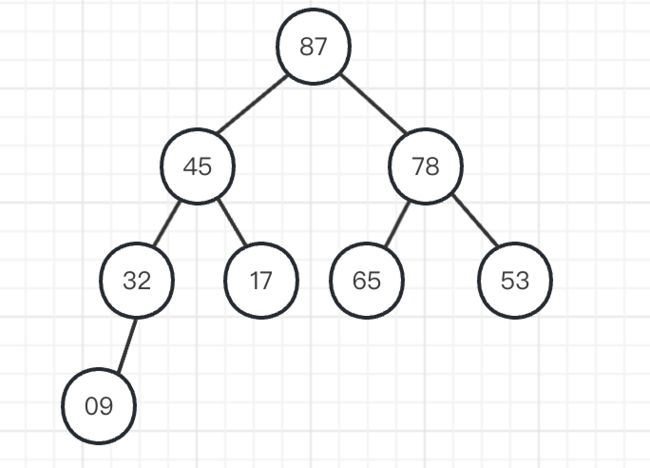
输出堆顶之后：
将最左下角的叶子节点放到堆顶，然后开始向下调整



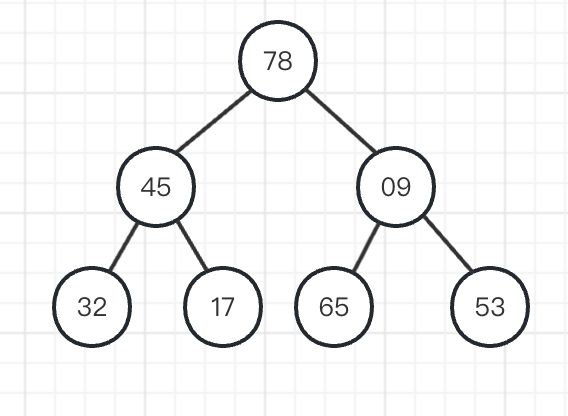
输出第一个就完成了，剩下类似。
时间复杂度：建堆时间复杂度$O(n)$，插入删除时间复杂度：$O(lo{g}_{2}n)$总得排序时间复杂度最坏最好平均都一样，$O(nlo{g}_{2}n)$
空间复杂度：$O(1)$
堆排序不稳定。

归并排序

二路归并，每次两个数组合成一个有序的数组。递归的合成每一个子区间。

空间复杂度：$O(n)$
时间复杂度：每趟归并的时间复杂度为$O(n)$,需要进行$logn$次归并，所以时间复杂度为$O(nlogn)$
二路归并排序算法是稳定的。

基数排序

• MSD最高位优先
• LSD最低位优先

算法思想：将一个数分成若干个关键字进行收集排序。收集若干轮，数组有序。

时间复杂度：$O(d(n+r))$
空间复杂度：$O(r)$
基数排序是稳定的。

各种排序算法性质的比较