深度学习之图像分类（二十）-- Transformer in Transformer(TNT)网络详解

深度学习之图像分类（二十）Transformer in Transformer(TNT)网络详解

本节学习 Transformer 嵌入 Transformer 的融合网络 TNT，思想自然，源于华为，值得一看。

1. 前言

Transformer in Transformer(TNT) 是华为团队 2021 的文章，论文为 Transformer in Transformer，并且表达的思想非常简单和自然。在原始的 Transformer 中，例如 ViT 中，对图片进行切片处理，切成了 $16\times 16$ 的 patch，Multi-Head Self-Attention 编码的是 patch 与 patch 之间的信息，也就是例如一个人脸图片，编码眼睛和嘴巴之间的相应权重。但是对于 patch 内部却没有进行很精细的编码，也就是说图片输入本身的“局部性”特性没有很好的利用上。一个很自然的想法就是，那我把 patch 直接变小好了，例如变为 $4\times 4$ 的大小，但是这样的话大大增加了 token 的数量，也增加了 Transformer 模型的计算量。此外之前微软团队的 Swin 工作也提到说，考虑把 key 值共享在一个小的 location 里可以对应于图像的局部性。那么，我们可以将大的 patch 再进行切片，在 patch 内部做一个 Multi-Head Self-Attention，将 key 值共享在 patch 内部，这样就能够兼顾“局部性”以及计算量。

事实上，Transformer in Transformer 和 U2Net (Unet in Unet) 有异曲同工之妙！

2. TNT Block

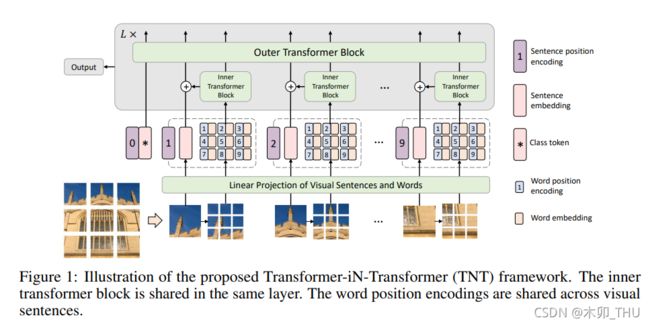
patch 内部的信息交流也非常重要，特别是对于精细结构而言。作者将 $16\times 16$ 的 patch 称为 visual sentences，将 patch 再进行切片出来的例如 $4\times 4$ 的更小的 patch 称为 visual word。这样 patch 内部进行自注意力机制研究哪里比较重要，patch 之间通过自注意力机制研究彼此之间的关系，能帮助我们增强特征的表示能力。此外，这样的小范围的 transformer 并不会增加太大的计算量。

让我们一步一步看看它是怎么实现的。

首先给定一个 2D 图像，我们通常将其进行切片形成 $\mathcal{X}=\left[X^1,X^2,\cdots ,X^n\right]\in {\mathbb{R}}^{n\times p\times p\times 3}$， 即切成 $n$ 个 patch，每个 patch 是 $p\times p\times 3$，3 为 RGB 通道，$p$ 为 patch 的分辨率。此后我们对单个 patch 再进行切分，切成 $m$ 个 sub-patch，得到 visual sentence 对应的一系列的 visual words：
$$X^i\to \left[x^{i,1},x^{i,2},\cdots ,x^{i,m}\right]$$
其中 $x^{i,j}\in {\mathbb{R}}^{s\times s\times 3}$，3 为 RGB 通道，$s$ 为 sub-patch 的分辨率，$x^{i,j}$ 表示第 $i$ 个 patch 的第 $j$ 个 sub-patch。例如一个 $16\times 16$ 的 patch 可以再被切为 16 个 $4\times 4$ 的 patch，则 $m=16,s=4$。对于每个 sub-patch，首先将它们进行展平（向量化 vectorization），然后经过一个全连接层进行编码：
$$Y^i=\left[y^{i,1},y^{i,2},\cdots ,y^{i,m}\right],y^{i,j}=FC\left(\mathrm{Vec}\left(x^{i,j}\right)\right)$$
然后将它们经过一个非常普通的由 Multi-Head Self-Attention 和 MLP 组成的 Transformer block 进行 patch 内部的 Transformer 操作，LN 则是 Layer Normalization 层，其中下标 $l$ 表示第几个 inner transform block：
$$\begin{array}{rl}{Y}_l^{\prime i}& =Y_{l-1}^i+\mathrm{MSA}\left(LN\left(Y_{l-1}^i\right)\right)\\ Y_l^i& =Y_l^{\prime i}+\mathrm{MLP}\left(LN\left(Y_l^{\prime i}\right)\right)\end{array}$$
得到 patch 内部经过注意力机制变换后的新的 sub-patch 表示，对其进行编码得到和对应 patch 相同大小的编码，与原始 patch 进行加和。这里的 $W_{l-1},b_{l-1}$ 对应的就是一个全连接层的权重和偏置，但是在源码中这里并没有使用偏置 self.proj = nn.Linear(num_words * inner_dim, outer_dim, bias=False)。
$$Z_{l-1}^i=Z_{l-1}^i+\mathrm{Vec}\left(Y_{l-1}^i\right)W_{l-1}+b_{l-1}$$
patch token 结合了自身切片后进行变换后的信息在馈入 outer transformer block 就得到了下一层的新 token。
$$\begin{array}{rl}{\mathcal{Z}}_l^{\prime i}& ={\mathcal{Z}}_{l-1}^i+\mathrm{MSA}\left(LN\left({\mathcal{Z}}_{l-1}^i\right)\right)\\ {\mathcal{Z}}_l^i& ={\mathcal{Z}}^{\prime i}+\mathrm{MLP}\left(LN\left({\mathcal{Z}}_l^{\prime i}\right)\right)\end{array}$$
这些总结出来就是：
$${\mathcal{Y}}_l,{\mathcal{Z}}_l=\mathrm{TNT}\left({\mathcal{Y}}_{l-1},{\mathcal{Z}}_{l-1}\right)$$
在 TNT block 中，inner transformer block 用于捕捉局部区域之间的特征关系，而 outer transformer block 则用于捕捉区域之间的联系。将 inner transformer block 的输出加到 outer transformer block 的输入上，这其实就像类似上级向下级传达任务（分类猫狗），下级首先形成一个初步意见（初始token），然后每个小组内部先进行讨论沟通交流，整合意见之后交给小组长（token 相加），小组长共同开会进行交流沟通得到一个意见之间的融合，再传递给上级。这种组内部的交流沟通在生活中非常常见。

In our TNT block, the inner transformer block is used to model the relationship between visual words for local feature extraction, and the outer transformer block captures the intrinsic information from the sequence of sentences. By stacking the TNT blocks for L times, we build the transformerin-transformer network. Finally, the classification token serves as the image representation and a fully-connected layer is applied for classification.

TNT 网络结构如下所示，Depth 为 block 重复的次数。

3. Position encoding

很多工作表示了，位置编码非常重要，那么每个 sub-patch 对应的 token 怎么进行位置编码呢？在 TNT 中，不同 sentence 中的 words 共享位置编码，即 $E_{word}$ 表示的是 sub-patch 在 patch 中的位置，这个在各个大 patch 中是一致的。
$$\begin{gathered} {\mathcal{Z}}_0\leftarrow {\mathcal{Z}}_0+E_{\text{sentence }} \\ {Y}_0^i\leftarrow Y_0^i+E_{word},i=1,2,\cdots ,n \end{gathered}$$

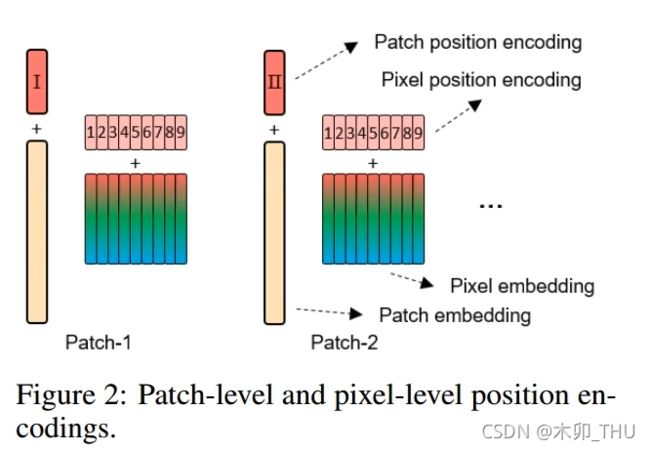
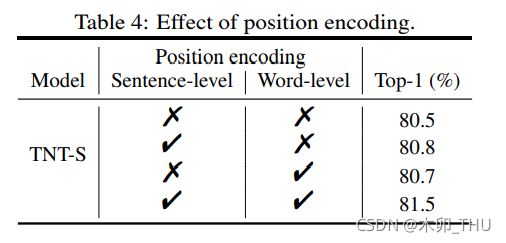
实验也发现，两个都使用位置编码可以得到更好的效果，但是在这篇 paper 中就没有去讨论使用绝对还是相对位置编码，1D 还是 2D 位置编码，以及把位置编码和 query 点乘构建 Attention 的一部分了。

4. 复杂度计算分析

对于原论文的描述，我一直存在疑惑，希望得到大家的解答。

一个标准的 Transformer block 包含两部分，Multi-head Self-Attention 和 multi-layer perceptron. 其中 Multi-head Self-Attention 的计算 FLOPs 为 $2nd\left(d_k+d_v\right)+n^2\left(d_k+d_v\right)$，其中 $n$ 为 token 的数量，$d$ 为 token 的维度，query 和 key 的维度都是 $d_k$，value 的维度为 $d_v$。MLP 对应的 FLOPs 则为 $2n{d}_{v}r{d}_v$，其中 $r$ 通常取 4，为第一个 全连接层维度扩展的倍数。通常呢这个 $d_k=d_v=d$ 。当不考虑 bias 以及 LN 时，一个标准的 transformer block 的 FLOPs 为 ：
$${\mathrm{FLOPs}}_T=2nd\left(d_k+d_v\right)+n^2\left(d_k+d_v\right)+2nddr=2nd(6d+n)$$
MLP 对应的 FLOPs 很好理解，一个 $nddr$ 是第一个全连接层从 $d$ 扩展维度到 $rd$；一个 $nddr$ 是第一个全连接层从 $rd$ 还原到 $d$。但是 MSA 的 FLOPs 就不是那么好理解了。$2nd{d}_k$ 是计算 $n$ 个 token 对应的 key 和 query，$nd{d}_v$ 是计算 $n$ 个 token 对应的 value，那前面的 2 怎么理解呢？此外，$n^2\left(d_k+d_v\right)$ 应该对应的是计算 Attention 矩阵以及对 $d_v$ 进行加权求和。计算 Attention 是会得到 $n^2$ 对 key 和 query 点乘，也应该是 $n^2{d}_k$？$n$ 个新 token，每个源自 $n$ 个 value 的加权求和，那么很自然是 $n^2{d}_v$。其中 $n{d}_v$ 表示一个新 token 是 $n$ 个 value 的加权求和。

我认为的一个标准的 transformer block 的 FLOPs 为 ：

• 计算 query：$W_{q}X=ndd$
• 计算 key：$W_{k}X=ndd$
• 计算 value：$W_{v}X=ndd$
• 计算 Attention $Q{K}^T$：$n^{2}d$
• 计算 value 的加权平均：$n^{2}d$
• 两层全连接层：$W_2{W}_{1}X=2ndrd$
• 所以应该是 $3ndd+2n^{2}d+8ndd=2nd(5.5d+n)$?
• 忽略了 残差 $nd$ 级别，忽略了偏置 $nd$ 级别，忽略了 LN。

一个标准的 transformer block 的参数量为 ：
$${\text{ Params }}_T=12dd\text{. }$$
而在 TNT 中，新增的一个 inner transformer block 的计算量和一个全连接层，所以 TNT 的 FLOPs 为 ：
$${\mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{S}}_{TNT}=2nmc(6c+m)+nmcd+2nd(6d+n)$$
其中 $2nmc(6c+m)$ 为 inner transformer block，$2nd(6d+n)$ 为 outer transformer block，$nmcd$ 为那个全连接层，需要从 $m\times c$ 维转为 $n\times d$ 维。相应的 TNT 的参数量为:
$${\text{ Params }}_{TNT}=12cc+mcd+12dd\text{. }$$
当 $c\ll d$ 且 $O(m)\approx O(n)$ 时候，例如 $d=384,n=196,c=24,m=16$ 时，TNT 的 FLOPs 为 1.14x，Params 为 1.08x。

但是 FLOPs 原论文算正确了吗？

5. 可视化结果

TNT 做分类等实验都表现出了一定的性能，其中和 DeiT 对比的可视化结果比较可观的反映出来了提升。可见局部信息在浅层得到了很好的保留，而随着网络的深入，表征逐渐变得更加抽象。

inner transformer 中不同的 query 位置（sub-patch）对应的激活部位可见，局部交流还是很有用的！

6. 代码

代码出处见 此处。

# 2021.06.15-Changed for implementation of TNT model
#            Huawei Technologies Co., Ltd. 
""" Vision Transformer (ViT) in PyTorch
A PyTorch implement of Vision Transformers as described in
'An Image Is Worth 16 x 16 Words: Transformers for Image Recognition at Scale' - https://arxiv.org/abs/2010.11929
The official jax code is released and available at https://github.com/google-research/vision_transformer
Status/TODO:
* Models updated to be compatible with official impl. Args added to support backward compat for old PyTorch weights.
* Weights ported from official jax impl for 384x384 base and small models, 16x16 and 32x32 patches.
* Trained (supervised on ImageNet-1k) my custom 'small' patch model to 77.9, 'base' to 79.4 top-1 with this code.
* Hopefully find time and GPUs for SSL or unsupervised pretraining on OpenImages w/ ImageNet fine-tune in future.
Acknowledgments:
* The paper authors for releasing code and weights, thanks!
* I fixed my class token impl based on Phil Wang's https://github.com/lucidrains/vit-pytorch ... check it out
for some einops/einsum fun
* Simple transformer style inspired by Andrej Karpathy's https://github.com/karpathy/minGPT
* Bert reference code checks against Huggingface Transformers and Tensorflow Bert
Hacked together by / Copyright 2020 Ross Wightman
"""
import torch
import torch.nn as nn
from functools import partial
import math

from timm.data import IMAGENET_DEFAULT_MEAN, IMAGENET_DEFAULT_STD
from timm.models.helpers import load_pretrained
from timm.models.layers import DropPath, to_2tuple, trunc_normal_
from timm.models.resnet import resnet26d, resnet50d
from timm.models.registry import register_model


def _cfg(url='', **kwargs):
    return {
        'url': url,
        'num_classes': 1000, 'input_size': (3, 224, 224), 'pool_size': None,
        'crop_pct': .9, 'interpolation': 'bicubic',
        'mean': IMAGENET_DEFAULT_MEAN, 'std': IMAGENET_DEFAULT_STD,
        'first_conv': 'patch_embed.proj', 'classifier': 'head',
        **kwargs
    }


default_cfgs = {
    'tnt_s_patch16_224': _cfg(
        mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5),
    ),
    'tnt_b_patch16_224': _cfg(
        mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5),
    ),
}


def make_divisible(v, divisor=8, min_value=None):
    min_value = min_value or divisor
    new_v = max(min_value, int(v + divisor / 2) // divisor * divisor)
    # Make sure that round down does not go down by more than 10%.
    if new_v < 0.9 * v:
        new_v += divisor
    return new_v


class Mlp(nn.Module):
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x


class SE(nn.Module):
    def __init__(self, dim, hidden_ratio=None):
        super().__init__()
        hidden_ratio = hidden_ratio or 1
        self.dim = dim
        hidden_dim = int(dim * hidden_ratio)
        self.fc = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, hidden_dim),
            nn.ReLU(inplace=True),
            nn.Linear(hidden_dim, dim),
            nn.Tanh()
        )

    def forward(self, x):
        a = x.mean(dim=1, keepdim=True) # B, 1, C
        a = self.fc(a)
        x = a * x
        return x


class Attention(nn.Module):
    def __init__(self, dim, hidden_dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.num_heads = num_heads
        head_dim = hidden_dim // num_heads
        self.head_dim = head_dim
        # NOTE scale factor was wrong in my original version, can set manually to be compat with prev weights
        self.scale = qk_scale or head_dim ** -0.5

        self.qk = nn.Linear(dim, hidden_dim * 2, bias=qkv_bias)
        self.v = nn.Linear(dim, dim, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop, inplace=True)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop, inplace=True)

    def forward(self, x):
        B, N, C = x.shape
        qk = self.qk(x).reshape(B, N, 2, self.num_heads, self.head_dim).permute(2, 0, 3, 1, 4)
        q, k = qk[0], qk[1]   # make torchscript happy (cannot use tensor as tuple)
        v = self.v(x).reshape(B, N, self.num_heads, -1).permute(0, 2, 1, 3)

        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, -1)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x


class Block(nn.Module):
    """ TNT Block
    """
    def __init__(self, outer_dim, inner_dim, outer_num_heads, inner_num_heads, num_words, mlp_ratio=4.,
                 qkv_bias=False, qk_scale=None, drop=0., attn_drop=0., drop_path=0., act_layer=nn.GELU,
                 norm_layer=nn.LayerNorm, se=0):
        super().__init__()
        self.has_inner = inner_dim > 0
        if self.has_inner:
            # Inner
            self.inner_norm1 = norm_layer(inner_dim)
            self.inner_attn = Attention(
                inner_dim, inner_dim, num_heads=inner_num_heads, qkv_bias=qkv_bias,
                qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
            self.inner_norm2 = norm_layer(inner_dim)
            self.inner_mlp = Mlp(in_features=inner_dim, hidden_features=int(inner_dim * mlp_ratio),
                                 out_features=inner_dim, act_layer=act_layer, drop=drop)

            self.proj_norm1 = norm_layer(num_words * inner_dim)
            self.proj = nn.Linear(num_words * inner_dim, outer_dim, bias=False)
            self.proj_norm2 = norm_layer(outer_dim)
        # Outer
        self.outer_norm1 = norm_layer(outer_dim)
        self.outer_attn = Attention(
            outer_dim, outer_dim, num_heads=outer_num_heads, qkv_bias=qkv_bias,
            qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
        self.outer_norm2 = norm_layer(outer_dim)
        self.outer_mlp = Mlp(in_features=outer_dim, hidden_features=int(outer_dim * mlp_ratio),
                             out_features=outer_dim, act_layer=act_layer, drop=drop)
        # SE
        self.se = se
        self.se_layer = None
        if self.se > 0:
            self.se_layer = SE(outer_dim, 0.25)

    def forward(self, inner_tokens, outer_tokens):
        if self.has_inner:
            inner_tokens = inner_tokens + self.drop_path(self.inner_attn(self.inner_norm1(inner_tokens))) # B*N, k*k, c
            inner_tokens = inner_tokens + self.drop_path(self.inner_mlp(self.inner_norm2(inner_tokens))) # B*N, k*k, c
            B, N, C = outer_tokens.size()
            outer_tokens[:,1:] = outer_tokens[:,1:] + self.proj_norm2(self.proj(self.proj_norm1(inner_tokens.reshape(B, N-1, -1)))) # B, N, C
        if self.se > 0:
            outer_tokens = outer_tokens + self.drop_path(self.outer_attn(self.outer_norm1(outer_tokens)))
            tmp_ = self.outer_mlp(self.outer_norm2(outer_tokens))
            outer_tokens = outer_tokens + self.drop_path(tmp_ + self.se_layer(tmp_))
        else:
            outer_tokens = outer_tokens + self.drop_path(self.outer_attn(self.outer_norm1(outer_tokens)))
            outer_tokens = outer_tokens + self.drop_path(self.outer_mlp(self.outer_norm2(outer_tokens)))
        return inner_tokens, outer_tokens


class PatchEmbed(nn.Module):
    """ Image to Visual Word Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_chans=3, outer_dim=768, inner_dim=24, inner_stride=4):
        super().__init__()
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)
        num_patches = (img_size[1] // patch_size[1]) * (img_size[0] // patch_size[0])
        self.img_size = img_size
        self.patch_size = patch_size
        self.num_patches = num_patches
        self.inner_dim = inner_dim
        self.num_words = math.ceil(patch_size[0] / inner_stride) * math.ceil(patch_size[1] / inner_stride)
        
        self.unfold = nn.Unfold(kernel_size=patch_size, stride=patch_size)
        self.proj = nn.Conv2d(in_chans, inner_dim, kernel_size=7, padding=3, stride=inner_stride)

    def forward(self, x):
        B, C, H, W = x.shape
        # FIXME look at relaxing size constraints
        assert H == self.img_size[0] and W == self.img_size[1], \
            f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
        x = self.unfold(x) # B, Ck2, N
        x = x.transpose(1, 2).reshape(B * self.num_patches, C, *self.patch_size) # B*N, C, 16, 16
        x = self.proj(x) # B*N, C, 8, 8
        x = x.reshape(B * self.num_patches, self.inner_dim, -1).transpose(1, 2) # B*N, 8*8, C
        return x


class TNT(nn.Module):
    """ TNT (Transformer in Transformer) for computer vision
    """
    def __init__(self, img_size=224, patch_size=16, in_chans=3, num_classes=1000, outer_dim=768, inner_dim=48,
                 depth=12, outer_num_heads=12, inner_num_heads=4, mlp_ratio=4., qkv_bias=False, qk_scale=None,
                 drop_rate=0., attn_drop_rate=0., drop_path_rate=0., norm_layer=nn.LayerNorm, inner_stride=4, se=0):
        super().__init__()
        self.num_classes = num_classes
        self.num_features = self.outer_dim = outer_dim  # num_features for consistency with other models

        self.patch_embed = PatchEmbed(
            img_size=img_size, patch_size=patch_size, in_chans=in_chans, outer_dim=outer_dim,
            inner_dim=inner_dim, inner_stride=inner_stride)
        self.num_patches = num_patches = self.patch_embed.num_patches
        num_words = self.patch_embed.num_words
        
        self.proj_norm1 = norm_layer(num_words * inner_dim)
        self.proj = nn.Linear(num_words * inner_dim, outer_dim)
        self.proj_norm2 = norm_layer(outer_dim)

        self.cls_token = nn.Parameter(torch.zeros(1, 1, outer_dim))
        self.outer_tokens = nn.Parameter(torch.zeros(1, num_patches, outer_dim), requires_grad=False)
        self.outer_pos = nn.Parameter(torch.zeros(1, num_patches + 1, outer_dim))
        self.inner_pos = nn.Parameter(torch.zeros(1, num_words, inner_dim))
        self.pos_drop = nn.Dropout(p=drop_rate)

        dpr = [x.item() for x in torch.linspace(0, drop_path_rate, depth)]  # stochastic depth decay rule
        vanilla_idxs = []
        blocks = []
        for i in range(depth):
            if i in vanilla_idxs:
                blocks.append(Block(
                    outer_dim=outer_dim, inner_dim=-1, outer_num_heads=outer_num_heads, inner_num_heads=inner_num_heads,
                    num_words=num_words, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale, drop=drop_rate,
                    attn_drop=attn_drop_rate, drop_path=dpr[i], norm_layer=norm_layer, se=se))
            else:
                blocks.append(Block(
                    outer_dim=outer_dim, inner_dim=inner_dim, outer_num_heads=outer_num_heads, inner_num_heads=inner_num_heads,
                    num_words=num_words, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale, drop=drop_rate,
                    attn_drop=attn_drop_rate, drop_path=dpr[i], norm_layer=norm_layer, se=se))
        self.blocks = nn.ModuleList(blocks)
        self.norm = norm_layer(outer_dim)

        # NOTE as per official impl, we could have a pre-logits representation dense layer + tanh here
        #self.repr = nn.Linear(outer_dim, representation_size)
        #self.repr_act = nn.Tanh()

        # Classifier head
        self.head = nn.Linear(outer_dim, num_classes) if num_classes > 0 else nn.Identity()

        trunc_normal_(self.cls_token, std=.02)
        trunc_normal_(self.outer_pos, std=.02)
        trunc_normal_(self.inner_pos, std=.02)
        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    @torch.jit.ignore
    def no_weight_decay(self):
        return {'outer_pos', 'inner_pos', 'cls_token'}

    def get_classifier(self):
        return self.head

    def reset_classifier(self, num_classes, global_pool=''):
        self.num_classes = num_classes
        self.head = nn.Linear(self.outer_dim, num_classes) if num_classes > 0 else nn.Identity()

    def forward_features(self, x):
        B = x.shape[0]
        inner_tokens = self.patch_embed(x) + self.inner_pos # B*N, 8*8, C
        
        outer_tokens = self.proj_norm2(self.proj(self.proj_norm1(inner_tokens.reshape(B, self.num_patches, -1))))        
        outer_tokens = torch.cat((self.cls_token.expand(B, -1, -1), outer_tokens), dim=1)
        
        outer_tokens = outer_tokens + self.outer_pos
        outer_tokens = self.pos_drop(outer_tokens)

        for blk in self.blocks:
            inner_tokens, outer_tokens = blk(inner_tokens, outer_tokens)

        outer_tokens = self.norm(outer_tokens)
        return outer_tokens[:, 0]

    def forward(self, x):
        x = self.forward_features(x)
        x = self.head(x)
        return x


def _conv_filter(state_dict, patch_size=16):
    """ convert patch embedding weight from manual patchify + linear proj to conv"""
    out_dict = {}
    for k, v in state_dict.items():
        if 'patch_embed.proj.weight' in k:
            v = v.reshape((v.shape[0], 3, patch_size, patch_size))
        out_dict[k] = v
    return out_dict


@register_model
def tnt_s_patch16_224(pretrained=False, **kwargs):
    patch_size = 16
    inner_stride = 4
    outer_dim = 384
    inner_dim = 24
    outer_num_heads = 6
    inner_num_heads = 4
    outer_dim = make_divisible(outer_dim, outer_num_heads)
    inner_dim = make_divisible(inner_dim, inner_num_heads)
    model = TNT(img_size=224, patch_size=patch_size, outer_dim=outer_dim, inner_dim=inner_dim, depth=12,
                outer_num_heads=outer_num_heads, inner_num_heads=inner_num_heads, qkv_bias=False,
                inner_stride=inner_stride, **kwargs)
    model.default_cfg = default_cfgs['tnt_s_patch16_224']
    if pretrained:
        load_pretrained(
            model, num_classes=model.num_classes, in_chans=kwargs.get('in_chans', 3), filter_fn=_conv_filter)
    return model


@register_model
def tnt_b_patch16_224(pretrained=False, **kwargs):
    patch_size = 16
    inner_stride = 4
    outer_dim = 640
    inner_dim = 40
    outer_num_heads = 10
    inner_num_heads = 4
    outer_dim = make_divisible(outer_dim, outer_num_heads)
    inner_dim = make_divisible(inner_dim, inner_num_heads)
    model = TNT(img_size=224, patch_size=patch_size, outer_dim=outer_dim, inner_dim=inner_dim, depth=12,
                outer_num_heads=outer_num_heads, inner_num_heads=inner_num_heads, qkv_bias=False,
                inner_stride=inner_stride, **kwargs)
    model.default_cfg = default_cfgs['tnt_b_patch16_224']
    if pretrained:
        load_pretrained(
            model, num_classes=model.num_classes, in_chans=kwargs.get('in_chans', 3), filter_fn=_conv_filter)
    return model