代码随想录算法训练营第二十天| LeetCode654. 最大二叉树、LeetCode617. 合并二叉树、LeetCode700. 二叉搜索树中的搜索、LeetCode98. 验证二叉搜索树

一、LeetCode654. 最大二叉树

        1：题目描述（654. 最大二叉树）

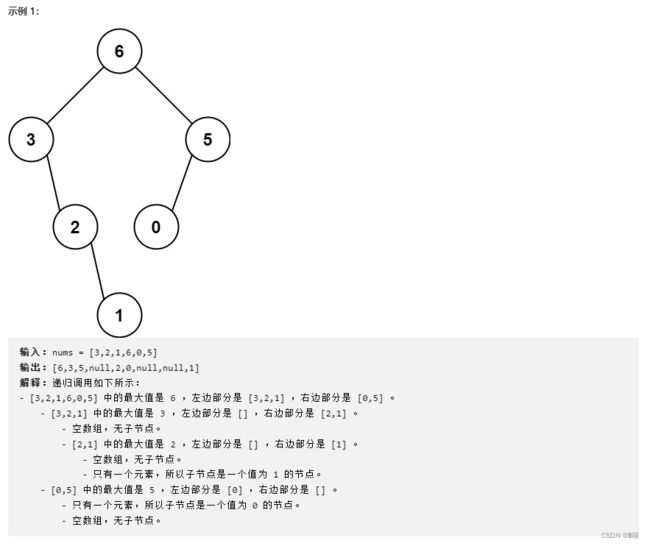
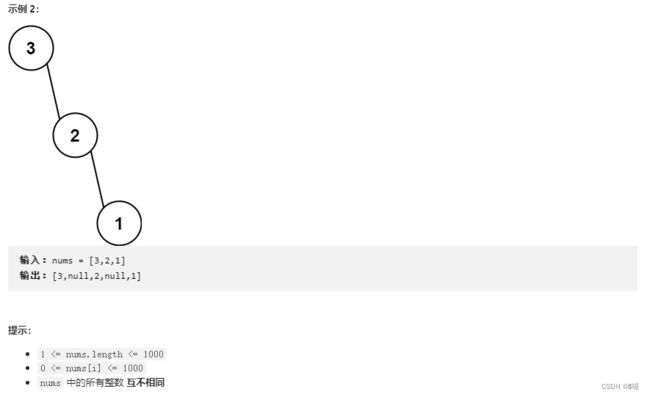
        给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

• 创建一个根节点，其值为 nums 中的最大值。
• 递归地在最大值 左边 的 子数组前缀上 构建左子树。
• 递归地在最大值 右边 的 子数组后缀上 构建右子树。

        返回 nums 构建的 最大二叉树 。

        2：解题思路

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        # 第一步：树为空（递归结束条件）
        if not nums:
            return None
        
        # 第二步：获取数组中，最大节点的值
        root_val = max(nums)
        root = TreeNode(root_val)

        # 第三步：获取最大值的下标
        max_ids = nums.index(root_val)

        # 第四步：进行分割数组，分割为左右子树
        nums_left = nums[:max_ids]
        nums_right = nums[max_ids+1:]

        # 第五步：递归
        root.left = self.constructMaximumBinaryTree(nums_left)
        root.right = self.constructMaximumBinaryTree(nums_right)

        return root

二、LeetCode617. 合并二叉树

        1：题目描述（617. 合并二叉树）

        给你两棵二叉树： root1 和 root2 。

        想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

        返回合并后的二叉树。

        注意: 合并过程必须从两个树的根节点开始。

        2：解题思路

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        if root1 == None:
            # 当root1为空，直接返回root2
            return root2
        if root2 == None:
            # 当root2为空，直接返回root1
            return root1
        # # 将root1和root2的值相加，得到新节点的值
        # root_val = root1.val + root2.val
        # # 定义一个新节点
        # root = TreeNode(root_val)

        # 直接使用root1，在root1的基础上进行操作
        root1.val += root2.val
        
        # 直接使用root1
        root1.left = self.mergeTrees(root1.left, root2.left)
        root1.right = self.mergeTrees(root1.right, root2.right)
        # 使用root
        # root.left = self.mergeTrees(root1.left, root2.left)
        # root.right = self.mergeTrees(root1.right, root2.right)

        return root1

三、LeetCode700. 二叉搜索树中的搜索

        1：题目描述（700. 二叉搜索树中的搜索）

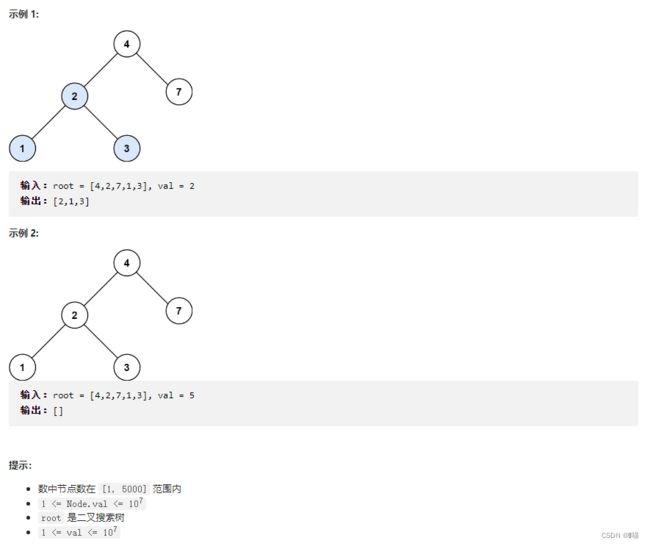
        给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

        你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

        2：解题思路

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        # 二叉搜索数-左子树的节点值小于根节点，右子树的节点值大于根节点
        # 树为空（递归终止条件）
        if not root:
            return None
        
        if root.val == val:
            return root          # 当前节点的值等于val，则直接返回当前节点
        if root.val > val:
            # 当前节点的值大于val，说明符合条件的节点在左子树，去遍历左子树
            node = self.searchBST(root.left, val)
            return node
        elif root.val < val:
            # 当前节点的值小于val，说明符合条件的节点在右子树，去遍历右子树
            node = self.searchBST(root.right, val)
            return node
        return None

四、LeetCode98. 验证二叉搜索树

        1：题目描述（98. 验证二叉搜索树）

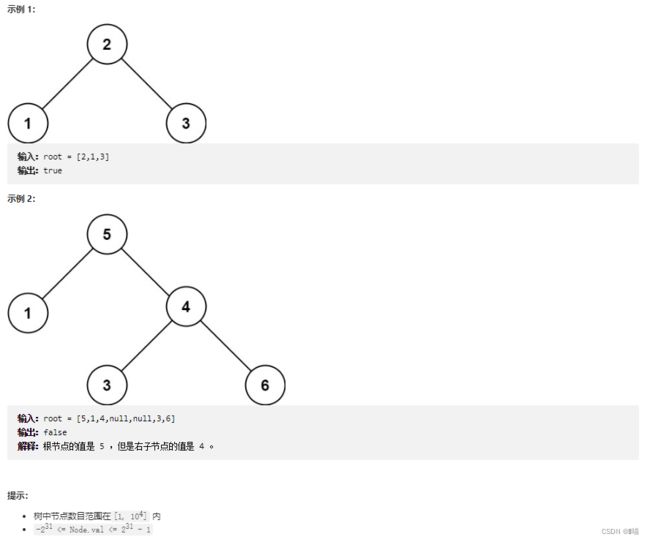
        给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

        有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

        2：解题思路

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        # 二叉搜索数的特性，使用中序遍历，遍历的结果中，节点的值是递增的

        # 递归
        # 定义一个变量，初始化的值为最小int值
        # 使用中序遍历，然后去比较变量的值是否小于当前节点的值，小于则将节点的值赋值给变量继续遍历，不小于则返回False
        min_value = -float("INF")
        def isvalid(root):
            nonlocal min_value
            if root == None:
                return True
            # 遍历左子树
            left_value = isvalid(root.left)
            # 比较前一个节点和当前节点
            if min_value >= root.val:
                # 若变量min_value的值大于等于当前节点的值，则说明不是二叉搜索树
                return False
            # 若变量min_value的值小于当前节点的值
            # 就将当前节点的值复制给min_value，进行下一个遍历节点的比较
            min_value = root.val
            # 遍历右子树
            right_value = isvalid(root.right)
            return left_value and right_value
        return isvalid(root)