数字逻辑理论——组合电路

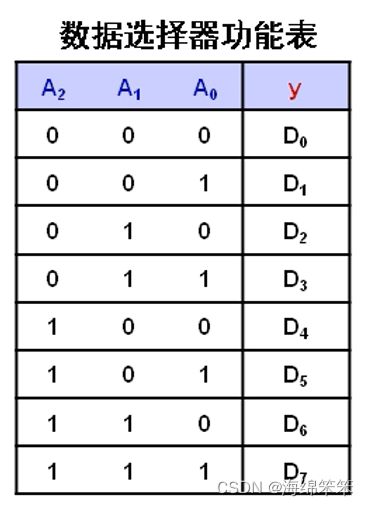
利用数据选择器设计组合逻辑电路

m：组合电路输入变量个数
n：数据选择器的控制端个数
（1）m=n
利用8选1数据选择器设计函数：F=AB’+A’C+BC’


待设计卡诺图：

F=∑(1,2,3,4,5,6)

（2）m>n
利用8选1数据选择器设计函数：F(A.B.C.D)=∑m(1,5,6,7,9,11,12,13,14)
卡诺图为：

根据数据选择器的结构，我们需要压缩成三变量（3输入：A,B,C）。
如何降维呢？ 使用展开定理

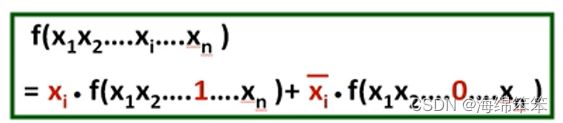
我们将变量D的取值拆出来：F(ABCD)=D*F(ABC)+D’*F(ABC)。
我们得到结果：

再对应数据选择器

可得到设计结果：

根据所需变量的情况灵活调整压缩变量；降维次数不宜超过2次，会大量增加电路复杂度。

利用中规模译码器芯片设计组合逻辑电路

实现方法：1、将逻辑函数描述为最小项之和的形式F= $\Sigma$m；2、若$\Sigma$项中包含最小项$m_i$，则相同序号值的译码器输出端Yi连接与非门的输入端。（译码输出低有效）

设计一个地址译码器，利用地址线$A_9,A_8,...,A_0$选择外设A,B,C。三个外设的地址分别是20H ~ 2FH，40H ~ 4FH，70H ~ 7FH。

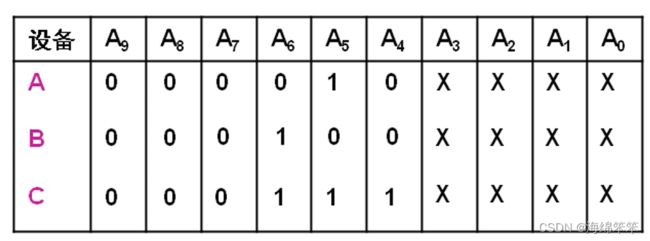
其中$A_6,A_5,A_4$可以唯一分别的对应A,B,C，可以用3-8译码器来进行选择。

奇偶校验器

检测数据传送和存取过程中是否产生错误的组合逻辑电路。

校验方式分为：奇（偶）校验，一般用异或门的运算检测结果。