代码随想录算法训练营第三十一天| 455.分发饼干、376. 摆动序列、53. 最大子序和
参考文章:代码随想录
参考视频:贪心算法,你想先喂哪个小孩?| LeetCode:455.分发饼干_哔哩哔哩_bilibili
解题思路:
为了满足更多的小孩,就不要造成饼干尺寸的浪费。
大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子,那么就应该优先满足胃口大的。
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
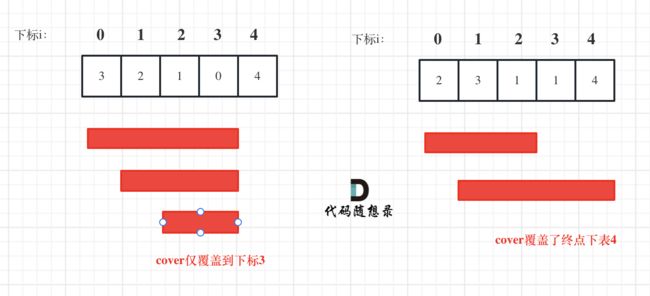
可以尝试使用贪心策略,先将饼干数组和小孩数组排序。
然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。
如图:
public class Leetcode455 {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int res = 0;
int index = s.length - 1;
for (int i = g.length - 1; i >= 0; i--) {
if (index >= 0 && s[index] >= g[i]) {
res++;
index--;
}
}
return res;
}
public int findContentChildren1(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int res = 0;
int index1 = g.length - 1;
int index2 = s.length - 1;
while (index1 >= 0 && index2 >= 0) {
if (s[index2] >= g[index1]) {
res++;
index1--;
index2--;
} else {
index1--;
}
}
return res;
}
}
376. 摆动序列
参考文章:代码随想录
参考视频:贪心算法,寻找摆动有细节!| LeetCode:376.摆动序列_哔哩哔哩_bilibili
解题思路:
本题要求通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
相信这么一说吓退不少同学,这要求最大摆动序列又可以修改数组,这得如何修改呢?
来分析一下,要求删除元素使其达到最大摆动序列,应该删除什么元素呢?
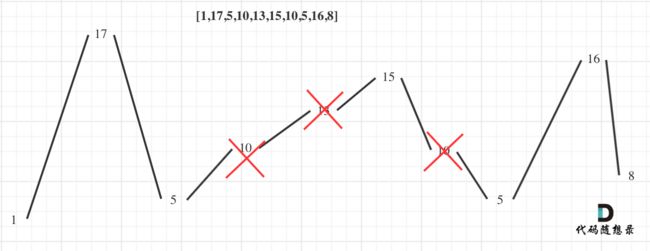
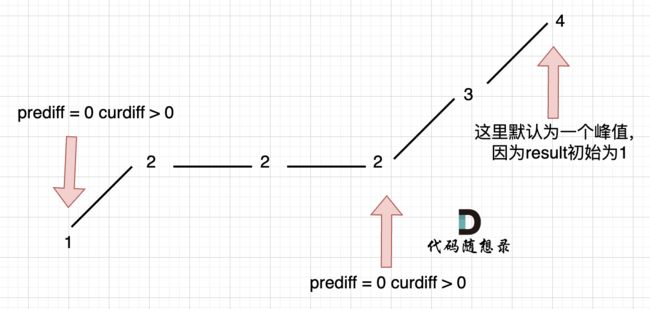
用示例二来举例,如图所示:
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
局部最优推出全局最优,并举不出反例,那么试试贪心!
(为方便表述,以下说的峰值都是指局部峰值)
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点
在计算是否有峰值的时候,大家知道遍历的下标i ,计算prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
这是我们思考本题的一个大题思路,但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
#情况一:上下坡中有平坡
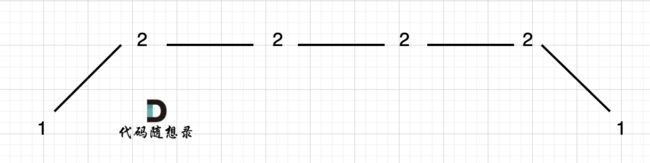
例如 [1,2,2,2,1]这样的数组,如图:
它的摇摆序列长度是多少呢? 其实是长度是3,也就是我们在删除的时候 要不删除左面的三个2,要不就删除右边的三个2。
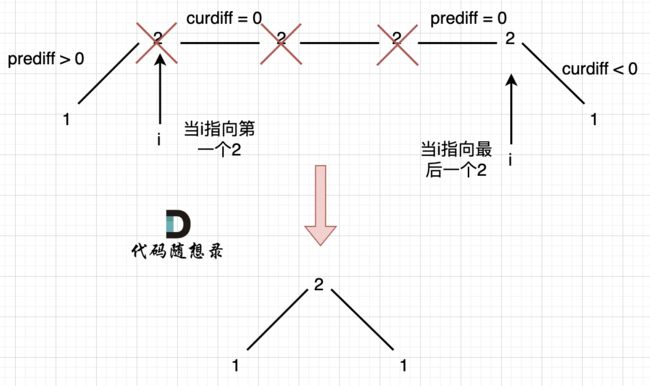
如图,可以统一规则,删除左边的三个2:
在图中,当i指向第一个2的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个2的时候 prediff = 0 && curdiff < 0。
如果我们采用,删左面三个2的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
#情况二:数组首尾两端
所以本题统计峰值的时候,数组最左面和最右面如果统计呢?
题目中说了,如果只有两个不同的元素,那摆动序列也是2。
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为2。
不写死的话,如果和我们的判断规则结合在一起呢?
可以假设,数组最前面还有一个数字,那这个数字应该是什么呢?
之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。
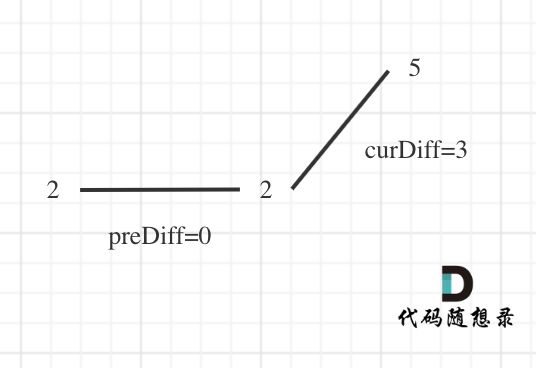
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即preDiff = 0,如图:
针对以上情形,result初始为1(默认最右面有一个峰值),此时curDiff > 0 && preDiff <= 0,那么result++(计算了左面的峰值),最后得到的result就是2(峰值个数为2即摆动序列长度为2)
情况三:单调坡度有平坡
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是2,因为 单调中的平坡 不能算峰值(即摆动)。
之所以版本一会出问题,是因为我们实时更新了 prediff。
那么我们应该什么时候更新prediff呢?
我们只需要在 这个坡度 摆动变化的时候,更新prediff就行,这样prediff在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
public class Leetcode376 {
public int wiggleMaxLength(int[] nums) {
int pre = 0;
int cur = 0;
int res = 0;
if (nums.length == 1) return 1;
for (int i = 0; i < nums.length - 1; i++) {
cur = nums[i + 1] - nums[i];
if (pre >= 0 && cur < 0 || pre <= 0 && cur > 0) {
res++;
pre = cur;
}
}
return res;
}
}53. 最大子序和
参考文章:代码随想录
参考视频:贪心算法的巧妙需要慢慢体会!LeetCode:53. 最大子序和_哔哩哔哩_bilibili
解题思路:
贪心贪的是哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
这相当于是暴力解法中的不断调整最大子序和区间的起始位置。
那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?
区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
if (count > result) result = count;
1
这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)。
public class Leetcode53 {
public int maxSubArray(int[] nums) {
int res = Integer.MIN_VALUE;
int count = 0;
for (int i = 0; i < nums.length; i++) {
count += nums[i];
if (count > res) {
res = count;
}
if (count < 0) count = 0;
}
return res;
}
}