写点题目(练习线段树)
昨天的学习要有更深的理解
来洛谷的第二块板子
如题,已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上 �x
-
将某区间每一个数加上 �x
-
求出某区间每一个数的和
输入格式
第一行包含三个整数 �,�,�n,m,p,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 �n 个用空格分隔的整数,其中第 �i 个数字表示数列第 �i 项的初始值。
接下来 �m 行每行包含若干个整数,表示一个操作,具体如下:
操作 11: 格式:1 x y k 含义:将区间 [�,�][x,y] 内每个数乘上 �k
操作 22: 格式:2 x y k 含义:将区间 [�,�][x,y] 内每个数加上 �k
操作 33: 格式:3 x y 含义:输出区间 [�,�][x,y] 内每个数的和对 �p 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 33 的结果。
输入输出样例
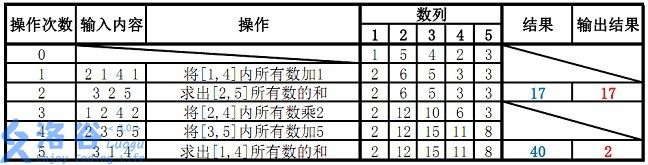
输入 #1复制
5 5 38 1 5 4 2 3 2 1 4 1 3 2 5 1 2 4 2 2 3 5 5 3 1 4
输出 #1复制
17 2
说明/提示
【数据范围】
对于 30%30% 的数据:�≤8n≤8,�≤10m≤10
对于 70%70% 的数据:�≤103n≤103,�≤104m≤104
对于 100%100% 的数据:�≤105n≤105,�≤105m≤105
除样例外,�=571373p=571373
(数据已经过加强^_^)
样例说明:
故输出应为 1717、22( 40 mod 38=240mod38=2 )
出自洛谷:https://www.luogu.com.cn/problem/P3373
看下面的图理解题目
和昨天的题目不一样,
由于题目对区间的处理不仅仅只有加减了,加了乘法了,所以要有两个lazy数组
一个记录加的系数
一个记录积的系数
而且对lazy数组的时候
要满足先处理乘法后处理加
这样不会影响精度,而且计算的时候要每次对p取余,便于后面的计算
ll lazy1[maxsize*4+50]={0};//lazy數組(乘法上的)
ll lazy2[maxsize*4+50]={0};//lazy数组(加法上的)
简单的定义
void lazyr(int l,int r,int p,ll la1,ll la2){//改变区间的和,并打上lazy标记
lazy1[p]=(lazy1[p]*la1)%mo;
lazy2[p]=(lazy2[p]*la1)%mo;
tree[p]=(tree[p]*la1)%mo;
lazy2[p]=(lazy2[p]+la2)%mo;
tree[p]=(tree[p]+la2*(r-l+1))%mo;
}对lazy数组以及tree的值的维护
子节点的lazy数组根据数学的方法更新自己的lazy数组就还原
void donm(int p,int l,int r){//k就是p节点的lazy值,向下传递lazy值
int mid=(l+r)/2;
lazyr(l,mid,lchid(p),lazy1[p],lazy2[p]);
lazyr(mid+1,r,rchid(p),lazy1[p],lazy2[p]);
lazy1[p]=1;//把lazy向下传递后自己的lazy清空
lazy2[p]=0;
}
//lazy下传的函数理解了lazy数组的话 对数组的处理基本上马上就可以看懂
然后和昨天就没有任何的区别了
上完整的代码看看
#include
#define maxsize 100000
typedef long long ll;//long long 麻烦好长的就用ll
ll tree[maxsize*4];//用數字模擬樹
ll lazy1[maxsize*4+50]={0};//lazy數組(乘法上的)
ll lazy2[maxsize*4+50]={0};//lazy数组(加法上的)
int a[100050];
ll ans=0;
void star(){
for(int h=1;h=r){//修改的区间完全包含当前区间
if(q==1){
lazyr(l,r,p,k,0);
return ;
}
if(q==2){
lazyr(l,r,p,1,k);
return ;
}
}
if(lazy1[p]!=1||lazy2[p]!=0)
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) updata(ll,rr,l,mid,lchid(p),k,q);
if(rr>mid) updata(ll,rr,mid+1,r,rchid(p),k,q);
sum(p);//对当前的节点要更新的
}
//区间修改
ll find(int ll,int rr,int l,int r,int p){
if(ll<=l&&rr>=r){//修改的区间完全包含当前区间
return ans=(ans+tree[p])%mo;
}
if(lazy1[p]!=1||lazy2[p]!=0)
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) find(ll,rr,l,mid,lchid(p));
if(rr>mid) find(ll,rr,mid+1,r,rchid(p));
return ans;
}
//区间求和
int main(){
int n,m;
star();
scanf("%d%d%d",&n,&m,&mo);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,1,n);//起始点为1,区间为1到n的建树
while(m--){
int q,w,e,r;
scanf("%d",&q);
if(q==2){
scanf("%d%d%d",&w,&e,&r);
updata(w,e,1,n,1,r,2);
}
else if(q==3){
ans=0;
scanf("%d%d",&w,&e);
find(w,e,1,n,1);
printf("%lld\n",ans);
}
else if(q==1){
scanf("%d%d%d",&w,&e,&r);
updata(w,e,1,n,1,r,1);
}
}
return 0;
} 和上一个很像(就是在上个题目 答案上进行了改动)
感觉难度并没上升多少,但是确实差点要了我的小命
数据有点大,对精度的要求有点高,我开的是long long 但是我忘记传参数的时候用了int
哎.2个小时的痛,反反复复的看代码7八遍,抓了折磨就得头发
void lazyr(int l,int r,int p,int la1,int la2){//改变区间的和,并打上lazy标记
lazy1[p]=(lazy1[p]*la1)%mo;
lazy2[p]=(lazy2[p]*la1)%mo;
tree[p]=(tree[p]*la1)%mo;
lazy2[p]=(lazy2[p]+la2)%mo;
tree[p]=(tree[p]+la2*(r-l+1))%mo;
}就一点点,就是ac和wa, 算是被上了一课
牢牢得记住!!!!!!!!!!!!!!!!
再来一个
# 【深基16.例1】淘汰赛
## 题目描述
有 $2^n$($n\le7$)个国家参加世界杯决赛圈且进入淘汰赛环节。已经知道各个国家的能力值,且都不相等。能力值高的国家和能力值低的国家踢比赛时高者获胜。1 号国家和 2 号国家踢一场比赛,胜者晋级。3 号国家和 4 号国家也踢一场,胜者晋级……晋级后的国家用相同的方法继续完成赛程,直到决出冠军。给出各个国家的能力值,请问亚军是哪个国家?
## 输入格式
第一行一个整数 $n$,表示一共 $2^n$ 个国家参赛。
第二行 $2^n$ 个整数,第 $i$ 个整数表示编号为 $i$ 的国家的能力值($1\leq i \leq 2^n$)。
数据保证不存在平局。
## 输出格式
仅一个整数,表示亚军国家的编号。
## 样例 #1
### 样例输入 #1
```
3
4 2 3 1 10 5 9 7
```
### 样例输出 #1
```
1
```
出自洛谷:P4715 【深基16.例1】淘汰赛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
一看题目,方法有点多
但是由于刚学了,线段树
灵光一闪!
哎,不就是取最大吗,把线段求和变成求线段最大就可以了
亚军就是tree[2]和tree[3]比较谁得能力小谁就是亚军
tree[2]就是冠军(没用)
但是每个节点要定义的就不只有一个值了
要有当前区间的最大值,以及最大值的编号(用结构体,就完全可以)
题目没有修改
连lazy标记都没有 直接薄纱!
上代码
#include
#include
struct node
{
int pow;
int naem;
} tree[100000*4];
void star()
{
for(int h=1; h<100000*4; h++)
{
tree[h].pow=0;
}
}
int powe[100000];
void bulid(int l,int r,int p)
{
if(l==r)
{
tree[p].pow=powe[l];
tree[p].naem=l;
return ;
}
int mid=(l+r)/2;
bulid(l,mid,p*2);
bulid(mid+1,r,p*2+1);
if(tree[p*2].pow>tree[p*2+1].pow)
{
tree[p].pow=tree[p*2].pow;
tree[p].naem=tree[p*2].naem;
}
else
{
tree[p].pow=tree[p*2+1].pow;
tree[p].naem=tree[p*2+1].naem;
}
}
int main()
{
int n;
scanf("%d",&n);
star();
for(int h=1; h<=(int)pow(2,n); h++)
scanf("%d",&powe[h]);
bulid(1,(int)pow(2,n),1);
if(tree[2].pow 没啥可讲的,板子都写出来了,这个完全没啥难度
耗时15m
下一个
# [USACO16DEC]Cities and States S
## 题目描述
To keep his cows intellectually stimulated, Farmer John has placed a large map of the USA on the wall of his barn. Since the cows spend many hours in the barn staring at this map, they start to notice several curious patterns. For example, the cities of Flint, MI and Miami, FL share a very special relationship: the first two letters of "Flint" give the state code ("FL") for Miami, and the first two letters of "Miami" give the state code ("MI") for Flint.
Let us say that two cities are a "special pair" if they satisfy this property and come from different states. The cows are wondering how many special pairs of cities exist. Please help them solve this amusing geographical puzzle!
为了训练奶牛们的智力,Farmer John 在谷仓的墙上放了一张美国地图。由于奶牛在谷仓里花了很多时间看这张地图,他们开始注意到一些奇怪的关系。例如,Flint 的前两个字母就是 Miami 所在的 `FL` 州,Miami 的前两个字母则是 Flint 所在的 `MI` 州。
确切地说,对于两个城市,它们的前两个字母互为对方所在州的名称。
我们称两个城市是一个一对“特殊的”城市,如果他们具有上面的特性,并且来自不同的省。奶牛想知道有多少对“特殊的”城市存在。请帮助他们解决这个有趣的地理难题!
## 输入格式
The first line of input contains $N$ ($1 \leq N \leq 200,000$), the number ofcities on the map.
The next $N$ lines each contain two strings: the name of a city (a string of at least 2 and at most 10 uppercase letters), and its two-letter state code (a string of 2 uppercase letters). Note that the state code may be something like ZQ, which is not an actual USA state. Multiple cities with the same name can exist, but they will be in different states.
第一行一个正整数 $N$,表示地图上的城市的个数。
接下来 $N$ 行,每行两个字符串,分别表示一个城市的名称($2 \sim 10$个大写字母)和所在州的代码($2$ 个大写字母)。可能出现类似 `ZQ` 的州代码,即并不真的是美国的一个州的代码。同一个州内不会有两个同名的城市。
## 输出格式
Please output the number of special pairs of cities.
输出特殊的城市对数。
## 样例 #1
### 样例输入 #1
```
6
MIAMI FL
DALLAS TX
FLINT MI
CLEMSON SC
BOSTON MA
ORLANDO FL
```
### 样例输出 #1
```
1
```
这题目看了一会
就是问你,要输出
字符串前两个字母调换的对数
大佬就是厉害,我还在想暴力,大佬的思路就是强
开一个地图,对字符前两个字母进行hash的简单变换(只要不计算到比你开的地图还大就可以了)
地图开二维的,因为我们讲地图的两个下标互换刚刚好就可以表示与自己匹配的特殊对(但是二维浪费了不少的空间,没关系题目的数据不大)
上代码
#include
int a[999][999];
int n,x,y,ans;
void star(){
for(int j=1;j<=998;j++){
for(int k=1;k<=998;k++){
a[j][k]=0;
}
}
}
int main(){
int n;
scanf("%d",&n);
getchar();
char lk[20],li[20];
for(int j=1;j<=n;j++){
scanf("%s",lk);
scanf("%s",li);
x=(lk[0]-'A')*27+lk[1];
y=(li[0] -'A')*27 + li[1];
if(x!=y){
a[y][x]++;
ans+=a[x][y];
}
}
printf("%d",ans);
return 0;
} 每次讲两个字符串录入的时候就判断一下与自己匹配的点有没有数有就代表有几队可以匹配,ans加上即可(没有的话j加0也是没关系的)
ok ok
今天撒花写谢幕!!!!!!