MOPSO 多目标粒子群算法
MOPSO 多目标粒子群算法
1、算法简介
多目标粒子群(MOPSO)算法是由CarlosA. Coello Coello等人在2004年提出,目的是将原来只能用在单目标上的粒子群算法(PSO)应用于多目标上。
1.1、相关知识点
支配(Dominance ) :在多目标优化问题中,如果个体p至少有一个目标比个体q好,而且个体p的所有目标都不比q差;那么称个体p支配个体q
序值(Rank):如果p支配q,那么p的序值比q低;如果p和q互不支配,那么p和q有相同的序值
拥挤距离(Crowding Distance):表示个体之间的拥挤程度,测量相同序值个体之间的距离。
帕累托(Pareto):https://blog.csdn.net/m0_59838738/article/details/121588306
粒子群算法(PSO):承接我的博客
2、算法描述
2.1、PSO 对比 MOPSO
PSO:
MOPSO注:
- 根据pareto支配原则,计算得到Archive集(存放当前的非劣解)计算局部最优pbest
- 计算Archive集中的拥挤度在Archive集选择全局最优gbest
- 更新粒子的速度和位置,并计算适应值更新Archive集(需注意防止溢出)
结论:可以看出PSO和MOPSO的大框架一致,MOPSO只是根据多目标问题改进了PSO中的pbest和gbest的选取方法
- pbest的选取:
- 单目标问题中,PSO可以根据适应度直接找出该粒子历史最好的位置;
- 多目标问题中,MOPSO找出该粒子历史最好的位置(保存于该粒子结构体的一个属性中);
- 如果在更新当前粒子的历史最好位置发现当前位置与历史最佳互不支配,0.5概率随机选一个;
- gbest的选取
- 单目标问题中,PSO可以根据适应度直接找出当前最好的粒子;
- 多目标问题中,MOPSO根据Pareto找出当前最好的粒子集合,至于最后精确到哪个粒子,找到最不拥挤的那个粒子;
2.2、密度的计算
与我的NSGA-II的博客的2.3拥挤距离类似,这里采用了网格法:
把目标空间用网格等分成小区域,以每个区域中包含的粒子数作为粒子的密度信息。粒子所在网格中包含的粒子数越多,其密度值越大,反之越小。
以二维目标空间最小化优化问题为例,密度信息估计算法的具体实现过程如下:
(1)假设我们现在得到一代种群粒子如下:
(2)根据输入的粒子坐标,可以确定每个维度的最大最小值,计算成坐标保存:即图示的两个黑点坐标
(3)划分格子,一般情况下我们会对边界进行一次膨胀,然后根据nGrid参数进行每个维度的等额划分:假设我们设置了参数nGrid = 3即每个维度划分3个网格
(4)存储格子信息,如上下界,格子编号等。然后根据粒子坐标即可统计格子内的粒子数。
3、算法流程图
4、代码实操
下面展示ZDT1~4系列问题的求解代码
4.1、代码
(1)文件目录:
(2)网格创建函数
function Grid = CreateGrid(pop, nGrid, alpha)
c = [pop.Cost];
%M = min(A,[],dim) 返回维度 dim 上的最小元素。例如,如果 A 为矩阵,则 min(A,[],2) 是包含每一行的最小值的列向量。
cmin = min(c, [], 2);
cmax = max(c, [], 2);
dc = cmax-cmin;
%网格边界外扩
cmin = cmin-alpha*dc;
cmax = cmax+alpha*dc;
nObj = size(c, 1);
%网格上下界
empty_grid.LB = [];
empty_grid.UB = [];
Grid = repmat(empty_grid, nObj, 1);
for j = 1:nObj
%y = linspace(x1,x2,n) 生成 n 个点。这些点的间距为 (x2-x1)/(n-1)。
cj = linspace(cmin(j), cmax(j), nGrid+1); % nGrid是设置好的参数
Grid(j).LB = [-inf cj];
Grid(j).UB = [cj +inf];
end
end
(3)支配计算函数1
function pop = DetermineDomination(pop)
nPop = numel(pop);
for i = 1:nPop
pop(i).IsDominated = false;
end
for i = 1:nPop-1
for j = i+1:nPop
% b = all(x <= y) && any(x(4)支配计算函数2
function b = Dominates(x, y)
if isstruct(x)
x = x.Cost;
end
if isstruct(y)
y = y.Cost;
end
b = all(x <= y) && any(x(5)网格查找函数,遍历粒子,统计网格
function particle = FindGridIndex(particle, Grid)
nObj = numel(particle.Cost);
nGrid = numel(Grid(1).LB);
particle.GridSubIndex = zeros(1, nObj);
for j = 1:nObj
particle.GridSubIndex(j) = ...
find(particle.Cost(j)(6)轮盘选择函数
function i = RouletteWheelSelection(P)
r = rand;
C = cumsum(P);
i = find(r <= C, 1, 'first');
end
(7)gbest选择函数,选一个当全局最优
function leader = SelectLeader(rep, beta)
% Grid Index of All Repository Members
GI = [rep.GridIndex];
% Occupied Cells
OC = unique(GI);
% Number of Particles in Occupied Cells
N = zeros(size(OC));
for k = 1:numel(OC)
N(k) = numel(find(GI == OC(k)));
end
% Selection Probabilities
P = exp(-beta*N);
P = P/sum(P);
% Selected Cell Index 轮盘选择
sci = RouletteWheelSelection(P);
% Selected Cell
sc = OC(sci);
% Selected Cell Members
SCM = find(GI == sc);
% 网格里可能还有多个粒子 再随机选一个
% Selected Member Index
smi = randi([1 numel(SCM)]);
% Selected Member
sm = SCM(smi);
% Leader
leader = rep(sm);
end
(8)绘图函数
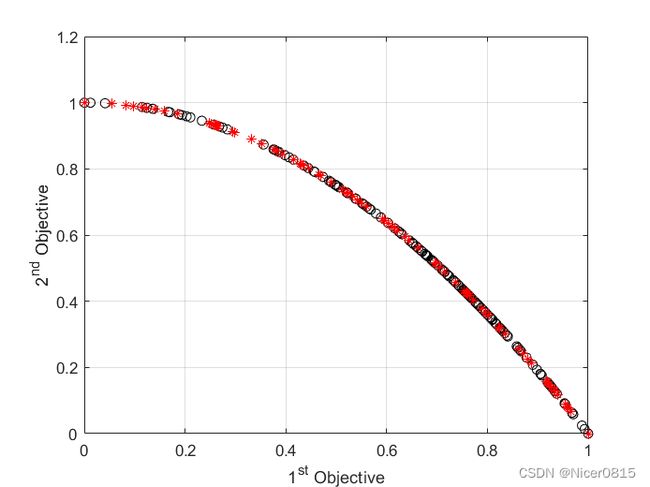
function PlotCosts(pop, rep)
pop_costs = [pop.Cost];
plot(pop_costs(1, :), pop_costs(2, :), 'ko');
hold on;
rep_costs = [rep.Cost];
plot(rep_costs(1, :), rep_costs(2, :), 'r*');
xlabel('1^{st} Objective');
ylabel('2^{nd} Objective');
grid on;
hold off;
end
(9)ZDT1~4
function z = ZDT1(x)
n = numel(x);
f1 = x(1);
g = 1+9/(n-1)*sum(x(2:end));
h = 1-sqrt(f1/g);
f2 = g*h;
z = [f1
f2];
end
function z = ZDT2(x)
n = numel(x);
f1 = x(1);
g = 1+9/(n-1)*sum(x(2:end));
h = 1-(f1/g)^2;
f2 = g*h;
z = [f1
f2];
end
function z = ZDT3(x)
n = numel(x);
f1 = x(1);
g = 1+9/(n-1)*sum(x(2:end));
%h = 1-(f1/g)^2; % ZDT2与3的不同之处
h = (1-(f1/g)^0.5-(f1/g)*sin(10*pi*f1));
f2 = g*h;
z = [f1
f2];
end
function z = ZDT4(x)
n = numel(x);
f1 = x(1);
sum=0;
for i=2:n
sum = sum+(x(i)^2-10*cos(4*pi*x(i)));
end
g = 1+9*10+sum;
h = (1-(f1/g)^0.5);
f2 = g*h;
z = [f1
f2];
end
(10)主函数
clc;
clear;
close all;
%% Problem Definition
CostFunction = @(x) ZDT3(x); % Cost Function
nVar = 5; % 5个决策变量
VarSize = [1 nVar]; % Size of Decision Variables Matrix
VarMin = 0; % Lower Bound of Variables
VarMax = 1; % Upper Bound of Variables
%% MOPSO Parameters
MaxIt = 200; % 迭代次数
nPop = 200; % 种群大小
nRep = 100; % 精英库
w = 0.5; % 惯性权重
wdamp = 0.99; % 惯性权重的衰减因子(阻尼)
c1 = 1; % 个体学习因子
c2 = 2; % 全局学习因子
nGrid = 7; % 每个维度的网格数
alpha = 0.1; % 膨胀率 网格边界外扩大小的因子
beta = 2; % Leader Selection Pressure
gamma = 2; % Deletion Selection Pressure
mu = 0.1; % 变异率
%% Initialization
empty_particle.Position = [];
empty_particle.Velocity = [];
empty_particle.Cost = [];
empty_particle.Best.Position = [];
empty_particle.Best.Cost = [];
empty_particle.IsDominated = [];
empty_particle.GridIndex = [];
empty_particle.GridSubIndex = [];
pop = repmat(empty_particle, nPop, 1);
for i = 1:nPop
pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
pop(i).Velocity = zeros(VarSize);
pop(i).Cost = CostFunction(pop(i).Position); % CostFunction = @(x) ZDT(x); 适应度
% Update Personal Best
pop(i).Best.Position = pop(i).Position;
pop(i).Best.Cost = pop(i).Cost;
end
% 计算种群的支配情况
pop = DetermineDomination(pop);
% 取出没有被支配的pop元素,存放到rep
rep = pop(~[pop.IsDominated]);
% 根据粒子分布画出网格
Grid = CreateGrid(rep, nGrid, alpha);
% 根据粒子位置确定所处网格
for i = 1:numel(rep)
rep(i) = FindGridIndex(rep(i), Grid);
end
%% MOPSO Main Loop
for it = 1:MaxIt
for i = 1:nPop
gbest = SelectLeader(rep, beta);
pop(i).Velocity = w*pop(i).Velocity ...
+c1*rand(VarSize).*(pop(i).Best.Position-pop(i).Position) ...
+c2*rand(VarSize).*(gbest.Position-pop(i).Position);
pop(i).Position = pop(i).Position + pop(i).Velocity;
pop(i).Position = max(pop(i).Position, VarMin);
pop(i).Position = min(pop(i).Position, VarMax);
pop(i).Cost = CostFunction(pop(i).Position);
% 更新i粒子历史最优
if Dominates(pop(i), pop(i).Best)
pop(i).Best.Position = pop(i).Position;
pop(i).Best.Cost = pop(i).Cost;
elseif Dominates(pop(i).Best, pop(i))
% Do Nothing
else
if rand<0.5
pop(i).Best.Position = pop(i).Position;
pop(i).Best.Cost = pop(i).Cost;
end
end
end
% Add Non-Dominated Particles to REPOSITORY
% 把更新后的rank = 1的粒子再加到rep
rep = [rep
pop(~[pop.IsDominated])]; %#ok
% Determine Domination of New Resository Members
% 上一代的Non-Dominated粒子和当前代的粒子进行支配判断
rep = DetermineDomination(rep);
% Keep only Non-Dminated Memebrs in the Repository
rep = rep(~[rep.IsDominated]);
% Update Grid
Grid = CreateGrid(rep, nGrid, alpha);
% Update Grid Indices
for i = 1:numel(rep)
rep(i) = FindGridIndex(rep(i), Grid);
end
% Check if Repository is Full
if numel(rep)>nRep
Extra = numel(rep)-nRep;
for e = 1:Extra
% 轮盘删一个,类似选取pbest的流程
rep = DeleteOneRepMemebr(rep, gamma);
end
end
% Plot Costs
figure(1);
PlotCosts(pop, rep);
pause(0.01);
% Show Iteration Information
disp(['Iteration ' num2str(it) ': Number of Rep Members = ' num2str(numel(rep))]);
% Damping Inertia Weight
w = w*wdamp;
end
之前漏掉的函数DeleteOneRepMemebr【sorry】
function rep = DeleteOneRepMemebr(rep, gamma)
% Grid Index of All Repository Members
GI = [rep.GridIndex];
% Occupied Cells
OC = unique(GI);
% Number of Particles in Occupied Cells
N = zeros(size(OC));
for k = 1:numel(OC)
N(k) = numel(find(GI == OC(k)));
end
% Selection Probabilities
P = exp(gamma*N);
P = P/sum(P);
% Selected Cell Index
sci = RouletteWheelSelection(P);
% Selected Cell
sc = OC(sci);
% Selected Cell Members
SCM = find(GI == sc);
% Selected Member Index
smi = randi([1 numel(SCM)]);
% Selected Member
sm = SCM(smi);
% Delete Selected Member
rep(sm) = [];
end