【数据结构】队列（循环队列和链队列）详细讲解各种操作

专栏【数据结构】

喜欢的诗句：更喜岷山千里雪 三军过后尽开颜。

音乐分享【勋章】

大一同学小吉，欢迎并且感谢大家指出我的问题

---

图片来源网络，如果侵权，请联系我 

目录

⭐队列的分类 

✨循环队列

优点

缺点

✨链队列

优点

缺点

⭐基本概念

✨队列

✨队头

✨队尾

⭐循环队列  详细操作 

定义

算法步骤

算法描述

为什么要“循环”

队空

队满

初始化

算法步骤

算法描述

求队列长度

算法步骤

算法描述

入队

算法步骤

算法描述

出队

算法步骤

算法描述

取队头元素

算法步骤

算法描述

遍历队列

算法步骤

算法描述

完整代码

⭐链队列  详细操作

定义

初始化

算法步骤

算法描述

入队

算法步骤

算法描述

出队

算法步骤

算法描述

取队头元素

算法步骤

算法描述

遍历队列

算法步骤

算法描述

完整代码

附加题

核心代码

---

⭐队列的分类 

✨循环队列

优点

1. 有效利用存储空间：因为循环队列可以重复使用已经出队的空间，所以相对于普通队列，它更能有效地利用存储空间。

2. 提高队列操作效率：由于循环队列的队尾和队头可以相连，所以插入和删除元素的操作都可以在 O(1) 的时间内完成，使得队列操作效率提高。

3. 方便实现算法：循环队列广泛应用于各种算法中，如 BFS（广度优先搜索）、模拟程序、操作系统等。这是因为循环队列具有较好的随机读取性能，方便实现算法。

缺点

1. 队列长度固定：循环队列的队列长度是固定的，无法动态扩容或缩小。如果队列长度过小，可能会导致入队操作失败，而队列长度过大则会浪费存储空间。

2. 难以判断队列是否为空：由于循环队列的队头和队尾可以相连，因此当队头指针和队尾指针重合时，无法判断队列是空还是满。为了解决这个问题，通常需要在循环队列中增加一个计数器，记录队列中元素的个数。

3. 不易实现动态删除操作：循环队列的底层存储结构通常采用数组实现，如果要删除队列中的某个元素，需要将该元素之后的所有元素依次前移，并将队尾指针重新指向前一个位置。这个操作比较繁琐，不如链式队列方便。

✨链队列

优点

1. 队列长度没有限制：链队列没有固定长度的限制，可以动态添加和删除队列中的元素，满足不同场景下的需求。

2. 插入和删除操作方便：由于链队列是采用链式存储结构实现的，因此在插入和删除操作时，只需要改变指针的引用即可，而不必像顺序队列那样进行元素的搬移操作。

3. 存储空间使用灵活：链队列只需要在堆上动态分配内存，因此它可以更灵活地使用存储空间，可以通过释放已经不再需要的节点来减少存储空间的浪费。

4. 难以出现队列满的情况：链队列不会出现队列满的情况，因为它可以动态增长，只要内存允许，就可以无限添加元素。

缺点

1. 空间开销：在使用链式存储结构时，每个节点需要额外的空间来存储指向下一个节点的指针，因此链队列的空间开销相对于顺序队列要大。

2. 难以实现随机访问：由于链队列的存储方式是链式的，因此在进行随机访问时，查找某个位置的节点需要从头节点开始依次遍历，效率比顺序队列低。

3. 无法利用CPU缓存：链队列中每个节点的存储空间不连续，因此使用CPU缓存会出现严重缓存不命中问题，导致效率降低。

综上所述，链队列适合插入、删除操作频繁，而对于需要快速随机访问的场景则不是很适合。当然，数据结构的选择需要综合考虑业务需求和实际情况，选择最适合的数据结构。

⭐基本概念

✨队列

一种先进先出的线性表，只允许在表的一端进行插入，另一端进行删除，类似于平时日常生活的排队

✨队头

允许删除的一端是队头（别搞反了）

✨队尾

允许插入的一端的队尾（别搞反了）

⭐循环队列  详细操作 

定义

算法步骤

1.使用一组地址连续的存储单元依次存放从队头到队尾的元素

2.定义头指针front  尾指针rear

算法描述

typedef struct SqQueue
{
	int *base;
	int front;//头指针
	int rear;//尾指针	
}SqQueue;

为什么要“循环”

初始化创建空队列时，令front = rear = 0 ,

每当插入新的队尾元素时，尾指针rear+1,

每当删除队头元素时，头指针front+1

因此，头指针始终指向队头元素，尾指针始终指向队尾元素的下一个位置

如图所示

 

假设当前队列分配的最大空间为6，那么当队列在上图（d）状态时，就不能再继续插入新的队尾元素，否则会出现溢出现象（数组非法越界），但是现在队列实际可用的空间还没有占满，那么这种现象就被叫做“假溢出”

变成“循环队列”就可以解决这个问题

循环队列里面，头，尾指针以及队列元素之间的关系不变，但是头，尾指针“按照环状+1”的操作可以通过“模”运算来实现。通过取模，头指针和尾指针就可以在顺序表空间里面以头尾衔接的方式“循环”移动

这样子

队空

S.front==S.rear

队满

(S.rear+1)%MAXSIZE==S.front

初始化

初始化就是动态分配一个预定义大小为MAXSIZE的数组空间

算法步骤

1.分配一个预定义大小为MAXSIZE的数组空间，base指向数组空间的首地址

2.将头指针和为指针置为0，表示空队列

算法描述

int init(SqQueue &S)
{
	S.base=new int[maxsize];
	if(!S.base) return -1;
	S.front=S.rear=0;//空队列
	return 1;
}

求队列长度

算法步骤

对于非循环队列，尾指针和头指针的差值就是队列长度，但是对于循环队列，这样子算出的长度可能为负数，所以得把差值加上maxsize，然后与maxsize求余

算法描述

int QueueLength(SqQueue S)
{
	return (S.rear-S.front+maxsize)%maxsize;
}

入队

在队尾插入一个新的元素

算法步骤

1.判断队列是否满，如果满，返回-1

2.将新元素插入队尾

（S.base[S.rear]=num）

3.队尾指针+1

算法描述

int EnQueue(SqQueue &S,int num)
{
	if((S.rear+1)%maxsize==S.front) return -1;
	S.base[S.rear]=num;
	S.rear=(S.rear+1)%maxsize;//入  队尾指针+1
	return 1;
}

出队

删除队头元素

算法步骤

1.判断队列是否满，如果满，返回-1

2.保存队头元素

3.队头指针+1

算法描述

int DeQueue(SqQueue &S)
{
	if(S.front==S.rear) return -1;
	cout<

取队头元素

算法步骤

当队列非空时，取出队头元素的值，队头指针不变

算法描述

int GetHead(SqQueue S)
{
    if(S.front!=S.rear)    //非空
        return S.base[S.front];
}

遍历队列

算法步骤

1.判断队列是否空，如果空，返回-1

2.头指针+1，向下遍历队列

算法描述

int Trance(SqQueue &S)
{
	if(S.front==S.rear) return -1;
	while(S.rear!=S.front)
	{
		cout<

完整代码

#include
using namespace std;

typedef struct SqQueue
{
	int *base;
	int front;//头指针
	int rear;//尾指针	
}SqQueue;

#define maxsize 16

//1
int init(SqQueue &S)
{
	S.base=new int[maxsize];
	if(!S.base) return -1;
	S.front=S.rear=0;
	return 1;
}
//3
int EnQueue(SqQueue &S,int num)
{
	if((S.rear+1)%maxsize==S.front) return -1;
	S.base[S.rear]=num;
	S.rear=(S.rear+1)%maxsize;//入  队尾指针+1
	return 1;
}
//4
int DeQueue(SqQueue &S)
{
	if(S.front==S.rear) return -1;
	cout<>num;
		switch(num)
		{
			case 1:
				if(init(S)) cout<<"初始化成功"<>n;
				for(int i=0;i>m;
					if(EnQueue(S,m)) cout<<"入队成功"<

⭐链队列  详细操作

定义

通常，链队列使用单链表来表示

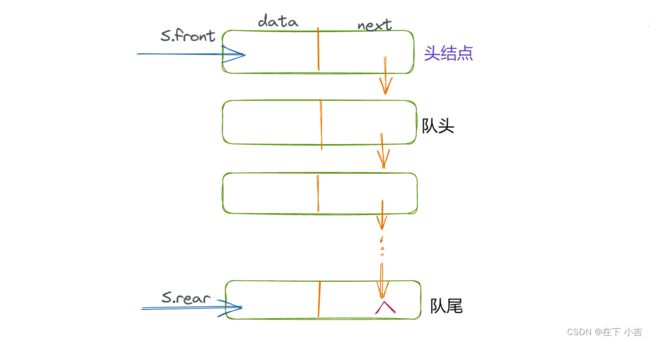
这里为了操作方便，在队头前面加上一个头结点，并且令头指针始终指向头结点 

typedef struct QNode{
	int data;
	struct QNode *next;
}QNode,*QueuePtr;

typedef struct{
	QueuePtr front;
	QueuePtr rear;
}LinkQueue;

初始化

初始化就是构造一个只有头结点的空队列

算法步骤

1.生成新结点作为头结点，️‍队头和队尾指针都指向这个结点️‍

2.头结点的指针域置空

算法描述

int init(LinkQueue &S)
{
	S.front=S.rear=new QNode;
	S.front->next=NULL;
	return 1;
}

入队

尾插法 

与循环队列入队不同，链队列入队不用判断队是否满，只要为入队元素动态分配一个内存空间即可

算法步骤

1.为入队元素分配一个内存空间，用指针p指向

2.将新结点的数据域置为e

3.将新结点插入到队尾

4.修改队尾指针为p

 

算法描述

int EnQueue(LinkQueue &S,int e)
{
	QNode *P;//注意是*P 不是 P
	P=new QNode;
	P->data=e;
	
	P->next=NULL;
	
	S.rear->next=P;//插入队尾
	S.rear=P;//修改队尾指针
	return 1;
}

出队

输出队头元素

出队前要判断队是否为空，出队后要释放队头元素的空间

算法步骤

1.判断队列是否为空，如果为空，那么返回-1

2.临时保存队头元素的值，方便释放空间

3.修改头指针的指针域，方便指向下一个结点

4.判断出队元素是否为最后一个结点，如果是，那么就将队尾指针重新赋值，指向头结点

5.释放原队头元素的空间

️‍注意：S.front->next为队头，S.front不为队头️‍

算法描述

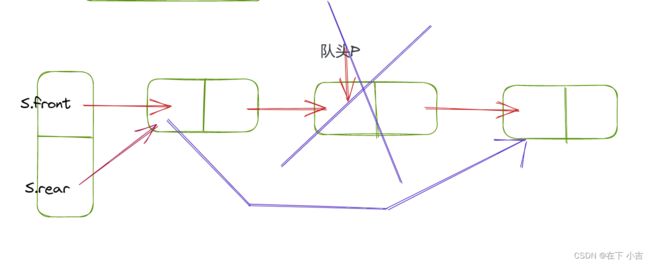
需要判断当队列中的最后一个元素被删后，队尾指针也会丢失，因此要对队尾指针重新赋值（指向头结点）

int DeQueue(LinkQueue &S)
{
	QNode *P;
	if(S.front==S.rear) return -1;
	
	P=S.front->next;//p指向队头元素
	cout<data<next=P->next;//修改头结点的指针域
	
	if(S.rear==P) S.rear=S.front;//如果最后一个元素被删，队尾指针指向头结点
	delete P;
	
	return 1;
}

取队头元素

算法步骤

1.判断队是否为空

2.输出队头元素

（S.front->next->data，不是S.front->data）

算法描述

int GetHead(LinkQueue S)
{
    if(S.front!=S.rear)    //非空
        return S.front->next->data;
}

遍历队列

算法步骤

1.创建新结点P

2.新结点P指向队头S.front->next

3.从队头遍历到队尾

算法描述

int Trance(LinkQueue &S)
{
	QNode *P;
	
	if(S.front==S.rear) return -1;
	P=S.front->next;
	while(P)
	{
		cout<data<<" ";
		P=P->next;
	}
	return 1;
}

完整代码

#include
using namespace std;

#define maxsize 16

typedef struct QNode{
	int data;
	struct QNode *next;
}QNode,*QueuePtr;

typedef struct{
	QueuePtr front;
	QueuePtr rear;
}LinkQueue;

//1
int init(LinkQueue &S)
{
	S.front=S.rear=new QNode;
	S.front->next=NULL;
	return 1;
}
//3
int EnQueue(LinkQueue &S,int e)
{
	QNode *P;//注意是*P 不是 P
	P=new QNode;
	P->data=e;
	
	P->next=NULL;
	
	S.rear->next=P;//插入队尾
	S.rear=P;//修改队尾指针
	return 1;
}
//4
int DeQueue(LinkQueue &S)
{
	QNode *P;
	if(S.front==S.rear) return -1;
	
	P=S.front->next;//p指向队头元素
	cout<data<next=P->next;//修改头结点的指针域
	
	if(S.rear==P) S.rear=S.front;//如果最后一个元素被删，队尾指针指向头结点
	delete P;
	
	return 1;
}
//5
int Trance(LinkQueue &S)
{
	QNode *P;
	
	if(S.front==S.rear) return -1;
	P=S.front->next;
	while(P)
	{
		cout<data<<" ";
		P=P->next;
	}
	return 1;
}
int main()
{
	LinkQueue S;
	int n,m;
	cout<<"请选择:"<>num;
		switch(num)
		{
			case 1:
				if(init(S)) cout<<"初始化成功"<>n;
				for(int i=0;i>m;
					if(EnQueue(S,m)) cout<<"入队成功"<

附加题

        假设以数组Q[m]存放循环队列中的元素，同时设置一个标志tag，以tag= 0 和tag= 1来区别在队头指针(front)和队尾指针(rear)相等时，队列状态为“空” 还是“满＂。

试编写与此结构相应的插入(Enqueue) 和删除(Dequeue) 算法。

核心代码

#define m 10                                    // 定义循环队列的长度
int Q[m];                                       // 循环队列数组
int front = 0, rear = 0;                        // 队头指针和队尾指针
int tag = 0;                                    // 标志位，用于区分队空和队满状态

void Enqueue(int x) {                           // 插入元素到队尾
    if ((rear + 1) % m == front && tag == 0) {   // 判断队满
        cout << "队列已满" << endl;
        return;
    }
    Q[rear] = x;                                // 插入元素到队尾
    rear = (rear + 1) % m;                      // 队尾指针加1
    tag = 0;                                    // 标志为0表示队列不为空
}

int Dequeue() {                                 // 删除队头元素
    if (front == rear && tag == 1) {            // 判断队空
        cout << "队列已空" << endl;
        return -1;
    }
    int x = Q[front];                           // 取出队头元素
    front = (front + 1) % m;                    // 队头指针加1
    tag = 1;                                    // 标志为1表示队列不为满
    return x;
}

如果大家有不明白的地方，或者文章有问题，欢迎大家在评论区讨论，指正 

Code over！