吴恩达深度学习第二周编程练习--识别猫的逻辑回归神经网络

吴恩达深度学习第二周编程练习--识别猫的逻辑回归神经网络

【识别猫】 的简单的神经网络，用python实现

注：开始编程前需要下载两个.h5文件，并将它们放到和python文件统一目录下（可到我的资源里下载）

百度云pycharm项目源码：https://pan.baidu.com/s/12q_Er1vJpeo-O8h_KQYgCQ

csdn .h5文件资源链接：https://download.csdn.net/download/qq_34290470/11583959

接下来就直接按照步骤将代码复制到python编程软件中即可（我这里使用的是Pycharm）

接下来我们一起来开始编程实现吧！！！

 

1.引入库：

numpy ：是用Python进行科学计算的基本软件包。
h5py：是与H5文件中存储的数据集进行交互的常用软件包。
matplotlib：是一个著名的库，用于在Python中绘制图表。

使用代码导入需要用到的库

import numpy as np
import matplotlib.pyplot as plt
import h5py

 

2.数据处理

• 定义load_dataset（）函数用于从.h5文件中导入数据
• 返回

  train_set_x_orig ：保存的是训练集里面的图像数据（本训练集有209张64x64的图像）。
  train_set_y_orig ：保存的是训练集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。
  test_set_x_orig ：保存的是测试集里面的图像数据（本训练集有50张64x64的图像）。
  test_set_y_orig ： 保存的是测试集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。
  classes ： 保存的是以bytes类型保存的两个字符串数据，数据为：[b’non-cat’ b’cat’]。

def load_dataset():
    train_dataset = h5py.File('train_catvnoncat.h5', "r")
    
    # 保存的是训练集里面的图像数据（本训练集有209张64x64的图像）。
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) 
    
    # 保存的是训练集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) 

    test_dataset = h5py.File('test_catvnoncat.h5', "r")
    
    # 保存的是测试集里面的图像数据（本训练集有50张64x64的图像）。
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    
    # 保存的是测试集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    # 保存的是以bytes类型保存的两个字符串数据，数据为：[b’non-cat’ b’cat’]。
    classes = np.array(test_dataset["list_classes"][:]) 

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
 

测试一下：

index=25
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset() # 加载数据集
plt.imshow(train_set_x_orig[index]) # 查看训练集中的图片
plt.show()

 测试结果：

 

打印出当前的训练标签值 

#打印出当前的训练标签值
# train_set_y是二维数组，使用np.squeeze的目的是压缩维度,即去掉shape中的1
# classe[0]='non-cat',classes[1]='cat'
print("y=" + str(train_set_y[:,index]) 
           + ", it's a "
           + classes[np.squeeze(train_set_y[:,index])].decode("utf-8") 
           + "' picture")

输出结果：

y=[1], it's a cat' picture

 

打印训练集信息：

m_train=train_set_x_orig.shape[0] # 训练集内的图片数量
m_test=test_set_x_orig.shape[0] # 测试集内的图片数量
num_px=train_set_x_orig.shape[1] #训练、测试集里面的图片的宽度和高度（均为64x64）

print("训练集中的数量：m_train=",m_train)
print("测试集中的数量：m_test=",m_test)
print("每张图片的宽/高：num_px=",num_px)
print("每张图片的大小：",train_set_x_orig[0].shape)
print("训练集_图片的维数：",train_set_x_orig.shape)
print("训练集_标签的维数: ",train_set_y.shape)
print("测试集_图片的维数：",test_set_x_orig.shape)
print("测试集_标签的维数：",test_set_y.shape)
 

输出结果：

训练集中的数量：m_train= 209
测试集中的数量：m_test= 50
每张图片的宽/高：num_px= 64
每张图片的大小： (64, 64, 3)
训练集_图片的维数： (209, 64, 64, 3)
训练集_标签的维数:  (1, 209)
测试集_图片的维数： (50, 64, 64, 3)
测试集_标签的维数： (1, 50)

 

3.向量化

每张图片的维度是(64,64,3)，我们需要将维度降为(64x64x3,1);因此每列代表一张平坦的图片
将训练集和测试集都转化为（12288,1）列向量的形式

数据标准化，由于RGB实际是值为0到255的三个向量。因此数据直接除以255，就可以将值缩放到0到1之间

# 每张图片的维度是(64,64,3)，我们需要将维度降为(64x64x3,1);因此每列代表一张平坦的图片
# 将训练集和测试集都转化为如上形式

train_set_x_flatten=train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten=test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T

print ("训练集降维最后的维度： " + str(train_set_x_flatten.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集降维之后的维度: " + str(test_set_x_flatten.shape))
print ("测试集_标签的维数 : " + str(test_set_y.shape))

# 数据标准化，由于RGB实际是值为0到255的三个向量。因此数据直接除以255，就可以将值缩放到0到1之间
train_set_x=train_set_x_flatten/255
test_set_x=test_set_x_flatten/255

输出结果：

训练集降维最后的维度： (12288, 209)
训练集_标签的维数 : (1, 209)
测试集降维之后的维度: (12288, 50)
测试集_标签的维数 : (1, 50)
 

 

4.构建神经网络

sigmoid激活函数

需要使用 sigmoid（w ^ T x + b） 计算来做出预测。

# sigmoid函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

初始化参数w和b

# 初始化参数

def initialize_with_zeros(dim):
    '''
    此函数为w创建一个维度为(dim,1)的向量，并将b初始化为0

    参数
    dim - w的矢量大小

    返回
    w - 维度为(dim,1)的初始化向量(对应权重)
    b - 初始化标量（对应偏差）

    '''
    w = np.zeros((dim, 1))
    b = 0

    # 利用断言来确保使用数据的正确
    assert (w.shape == (dim, 1))
    assert (isinstance(b, int) or isinstance(b, float))

    return (w, b)

实现一个计算成本函数及其渐变的函数propagate（）

def propagate(w, b, X, Y):
    '''
    实现前向和后向传播的成本函数及其梯度

    参数
    w - 权重，维度(num_p * num_px * 3,1)
    b - 偏差，标量
    X - 训练集，维度(num_p * num_px * 3,m_train)
    Y - 真实标签，维度(1,m_train)

    返回
    cost- 逻辑回归的负对数似然成本
    dw  - 相对于w的损失梯度，维度与w相同
    db  - 相对于b的损失梯度，维度与b相同

    '''
    m = X.shape[1]

    # 正向传播
    A = sigmoid(np.dot(w.T, X) + b)
    cost = (-1 / m) * np.sum((1 - Y) * np.log(1 - A) + Y * np.log(A))
    cost = np.squeeze(cost)

    # 反向传播
    dw = (1 / m) * np.dot(X, (A - Y).T)
    db = (1 / m) * np.sum(A - Y)

    # 使用断言确保数据的准确性
    assert (dw.shape == w.shape)
    assert (db.dtype == float)

    # 创建一个字典存储dw和db
    grads = {
        'dw': dw,
        'db': db
    }

    return (grads, cost)

梯度下降函数optimize

使用渐变下降更新参数。

目标是通过最小化成本函数 J来学习 w和b 。对于参数 θ ，更新规则是 θ=θ−α dθ，其中 α 是学习率。

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost):
    '''此函数通过运行梯度下降算法来优化w和b

    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数组。
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据的数量)
        num_iterations  - 优化循环的迭代次数
        learning_rate  - 梯度下降更新规则的学习率
        print_cost  - 每100步打印一次损失值

    返回：
        params  - 包含权重w和偏差b的字典
        grads  - 包含权重和偏差相对于成本函数的梯度的字典
        成本 - 优化期间计算的所有成本列表，将用于绘制学习曲线。'''

    costs = []  # 用于存储每一百次迭代的误差
    for i in range(num_iterations):

        grads, cost = propagate(w, b, X, Y)

        dw = grads['dw']
        db = grads['db']

        w = w - learning_rate * dw
        b = b - learning_rate * db

        # 可以选择每迭代一百次就打印一次误差
        if i % 100 == 0:
            costs.append(cost)
        if (print_cost) and (i % 100 == 0):
            print("迭代次数：", i, "误差：", cost)

    params = {
        "w": w,
        "b": b
    }
    grads = {
        'dw': dw,
        'db': db
    }

    return (params, grads, costs)

测试一下优化函数：

#测试optimize
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
params , grads , costs = optimize(w , b , X , Y , num_iterations=100 , learning_rate = 0.009 , print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))

测试结果为：
w = [[ 0.1124579 ]
 [ 0.23106775]]
b = 1.55930492484
dw = [[ 0.90158428]
 [ 1.76250842]]
db = 0.430462071679 

 

预测函数predict（）

optimize函数会输出已学习的w和b的值，我们可以使用w和b来预测数据集X的标签。

现在我们要实现预测函数predict（）。计算预测有两个步骤：

计算 Y^=A=σ(wTX+b)Y^=A=σ(wTX+b)
将a的值变为0（如果激活值<= 0.5）或者为1（如果激活值> 0.5），

然后将预测值存储在向量Y_prediction中。

def predict(w , b , X ):
    """
    使用学习逻辑回归参数logistic （w，b）预测标签是0还是1，

    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数据

    返回：
        Y_prediction  - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组（向量）

    """

    m  = X.shape[1] #图片的数量
    Y_prediction = np.zeros((1,m)) 
    w = w.reshape(X.shape[0],1)

    #计预测猫在图片中出现的概率
    A = sigmoid(np.dot(w.T , X) + b)
    for i in range(A.shape[1]):
        #将概率a [0，i]转换为实际预测p [0，i]
        Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
    #使用断言
    assert(Y_prediction.shape == (1,m))

    return Y_prediction

 

model()函数

通过调用之前实现的函数来构建逻辑回归模型

把上述所有函数统统整合到一个model()函数中，我们就只需要调用一个model()函数

def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
    """
    通过调用之前实现的函数来构建逻辑回归模型

    参数：
        X_train  - numpy的数组,维度为（num_px * num_px * 3，m_train）的训练集
        Y_train  - numpy的数组,维度为（1，m_train）（矢量）的训练标签集
        X_test   - numpy的数组,维度为（num_px * num_px * 3，m_test）的测试集
        Y_test   - numpy的数组,维度为（1，m_test）的（向量）的测试标签集
        num_iterations  - 表示用于优化参数的迭代次数的超参数
        learning_rate  - 表示optimize（）更新规则中使用的学习速率的超参数
        print_cost  - 设置为true以每100次迭代打印成本

    返回：
        d  - 包含有关模型信息的字典。
    """
    w , b = initialize_with_zeros(X_train.shape[0])

    parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)

    #从字典“参数”中检索参数w和b
    w , b = parameters["w"] , parameters["b"]

    #预测测试/训练集的例子
    Y_prediction_test = predict(w , b, X_test)
    Y_prediction_train = predict(w , b, X_train)

    #打印训练后的准确性
    print("训练集准确性："  , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
    print("测试集准确性："  , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")

    d = {
            "costs" : costs,
            "Y_prediction_test" : Y_prediction_test,
            "Y_prediciton_train" : Y_prediction_train,
            "w" : w,
            "b" : b,
            "learning_rate" : learning_rate,
            "num_iterations" : num_iterations }
    return d

测试一下训练结果，令迭代次数为2000，学习率为0.005

# 测试一下训练结果
d=model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

 输出结果:

迭代次数： 0 误差： 0.6931471805599453
迭代次数： 100 误差： 0.5845083636993086
迭代次数： 200 误差： 0.46694904094655476
迭代次数： 300 误差： 0.37600686694802077
迭代次数： 400 误差： 0.3314632893282513
迭代次数： 500 误差： 0.30327306747438293
迭代次数： 600 误差： 0.2798795865826048
迭代次数： 700 误差： 0.26004213692587574
迭代次数： 800 误差： 0.24294068467796623
迭代次数： 900 误差： 0.22800422256726066
迭代次数： 1000 误差： 0.21481951378449635
迭代次数： 1100 误差： 0.20307819060644985
迭代次数： 1200 误差： 0.1925442771670686
迭代次数： 1300 误差： 0.18303333796883503
迭代次数： 1400 误差： 0.17439859438448876
迭代次数： 1500 误差： 0.16652139705400335
迭代次数： 1600 误差： 0.15930451829756614
迭代次数： 1700 误差： 0.15266732471296504
迭代次数： 1800 误差： 0.1465422350398234
迭代次数： 1900 误差： 0.14087207570310162
测试集的准确性： 99.7 %
训练集的准确性： 99.99043062200957 %

 

5.数据可视化

# 可视化
costs=d['costs']
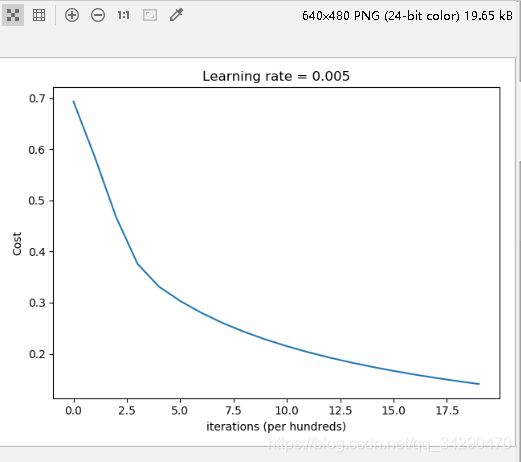
plt.plot(costs)
plt.title("Learning rate = 0.005")
plt.xlabel("iterations (per hundreds)")
plt.ylabel("Cost")
plt.show()

梯度下降优化

学习率α 决定了我们更新参数的速度。如果学习率过高，我们可能会“超过”最优值。同样，如果它太小，我们将需要太多迭代才能收敛到最佳值。这就是为什么使用良好调整的学习率至关重要的原因。

我们可以比较一下我们模型的学习曲线和几种学习速率的选择。也可以尝试使用不同于我们初始化的learning_rates变量包含的三个值，并看一下会发生什么。

learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
    print ("learning rate is: " + str(i))
    models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
    print ('\n' + "-------------------------------------------------------" + '\n')

for i in learning_rates:
    plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()

输出结果：

learning rate is: 0.01
测试集的准确性： 99.68 %
训练集的准确性： 99.99521531100478 %

-------------------------------------------------------

learning rate is: 0.001
测试集的准确性： 99.64 %
训练集的准确性： 99.88995215311004 %

-------------------------------------------------------

learning rate is: 0.0001
测试集的准确性： 99.36 %
训练集的准确性： 99.6842105263158 %

-------------------------------------------------------

 

注：有任何疑问请留言，看到了我就会回复。