AutoEncoder及Variational AutoEncoder模型

AutoEncoder及Variational AutoEncoder模型

一、AutoEncoder概述

• 作为一种无监督或者自监督算法，自编码器本质上是一种数据压缩算法。
• 从现有情况来看，无监督学习很有可能是一把决定深度学习未来发展方向的钥匙，在缺乏高质量打标数据的监督机器学习时代，若是能在无监督学习方向上有所突破对于未来深度学习的发展意义重大。
  
• 所谓自编码器（Autoencoder，AE），就是一种利用反向传播算法使得输出值等于输入值的神经网络，它先将输入压缩成潜在空间表征，然后将这种压缩后的空间表征重构为输出。
  
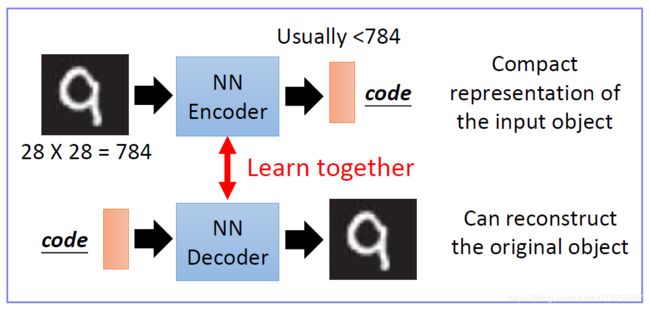
• 它的隐藏成层的向量具有降维的作用。所以，从本质上来讲，自编码器是一种数据压缩算法，其压缩和解压缩算法都是通过神经网络来实现的。
• AutoEncoder通常有两个方面的应用：
  1. 是数据去噪，
  2. 是为进行可视化而降维。
  3. 进行图像压缩
  4. 传统自编码器被用于降维或特征学习
• 自编码器在适当的维度和系数约束下可以学习到比PCA等技术更有意义的数据映射。

二、AutoEncoder结构

• 自编码器有如下三个特点：
  1. 数据相关性。就是指自编码器只能压缩与自己此前训练数据类似的数据，比如说我们使用mnist训练出来的自编码器用来压缩人脸图片，效果肯定会很差。
  2. 数据有损性。自编码器在解压时得到的输出与原始输入相比会有信息损失，所以自编码器是一种数据有损的压缩算法。
  3. 自动学习性。自动编码器是从数据样本中自动学习的，这意味着很容易对指定类的输入训练出一种特定的编码器，而不需要完成任何新工作。

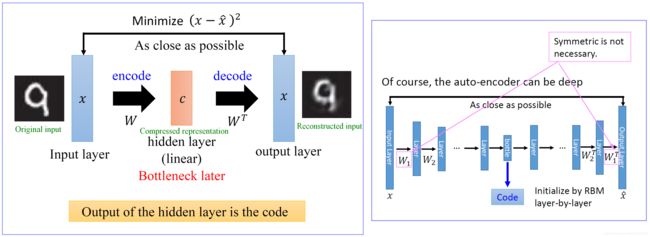
• 构建一个自编码器需要两部分：编码器（Encoder）和解码器（Decoder）。
  • 编码器将输入压缩为潜在空间表征，编码器会创建一个隐藏层（或多个隐藏层）包含了输入数据含义的低维向量。可以用函数 $f(x)$ 来表示，
  • 解码器将潜在空间表征重构为输出，即通过隐藏层的低维向量重建输入数据。可以用函数 $g(x)$ 来表示
• 编码函数 $f(x)$ 和解码函数 $g(x)$ 都是神经网络模型。
  

三、AutoEncoder模型的损失函数

• AE是一个自动编码器是一个非监督的学习模式，只需要输入数据，不需要label或者输入输出对的数据。
• 虽然AE是一个非监督学习算法，如果它的解码器是线性重建数据，可以用MSE来表示它的损失函数：
  
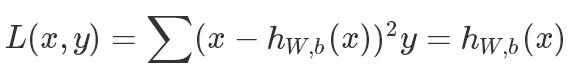
• 如果解码器用Sigmoid的激活函数，那主要用交叉上损失函数：
  

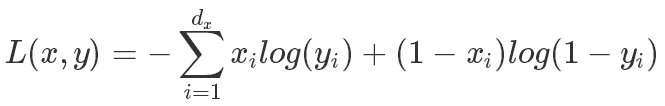
四、VAE 变分自动编码器

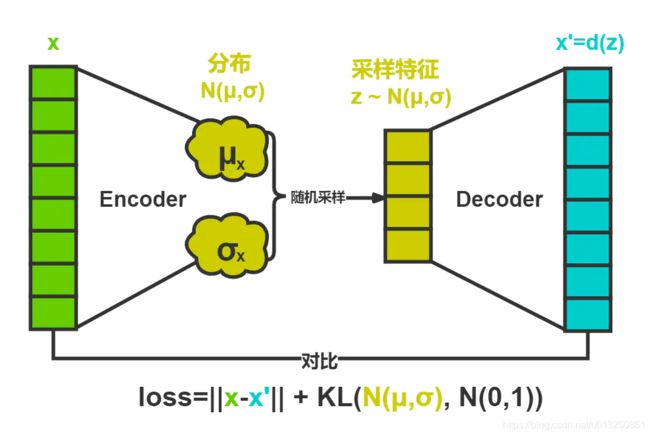
• VAE结构是一个经典的autocoder模型，网络的组成也是编码器、解码器、loss。
• VAE的机构和普通的AE结构有所不同。
• 普通的AE结构如下，解码器直接使用编码器的输出向量。
  
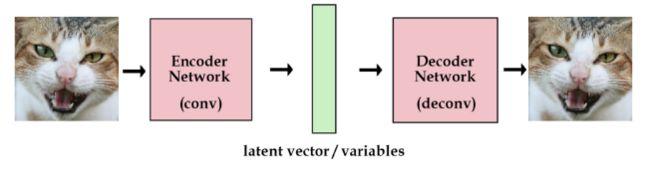
• 上面的模型已经可以训练任意图片了。但是，我们想建一个产生式模型，而不是一个只是储存图片的网络。
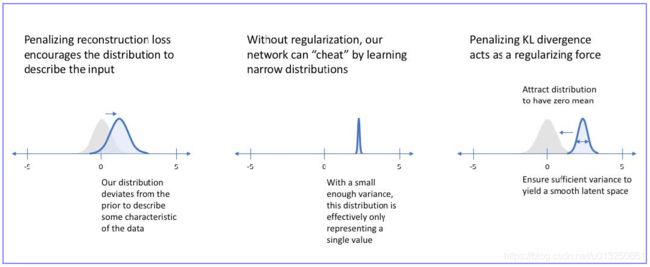
• 现在我们还不能产生任何未知的东西，因为我们不能随意产生合理的潜在变量。因为合理的潜在变量都是编码器从原始图片中产生的。这里有个简单的解决办法。我们可以对编码器添加约束，就是强迫它产生服从单位高斯分布的潜在变量。正是这种约束，把VAE和标准自编码器给区分开来了。
• VAE 的loss通常由两部分组成：首先是 reconstruction loss， 然后是KL散度($z$ 的分布和正态分布的差距)。
  
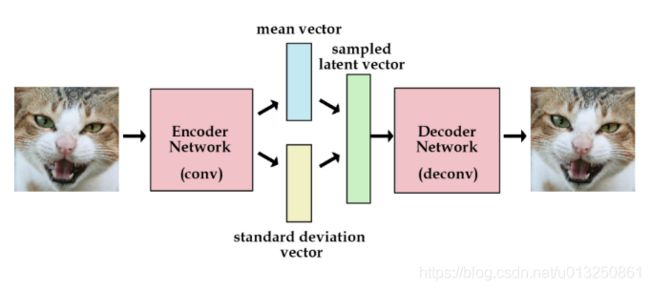
• 标准AutoEncoder的Encoder产生的是明确的、固定的 vector $h$，
• VAE 的 Encoder 会产生一个分布，这个分布用 均值 vector 和 标准差 vector来表示。
• VAE将经过神经网络编码后的隐藏层假设为一个标准的高斯分布，然后再从这个分布中采样一个特征，再用这个特征进行解码，期望得到与原始输入相同的结果，损失和AE几乎一样，只是增加编码推断分布与标准高斯分布的KL散度的正则项，显然增加这个正则项的目的就是防止模型退化成普通的AE，因为网络训练时为了尽量减小重构误差，必然使得方差逐渐被降到0，这样便不再会有随机采样噪声，也就变成了普通的AE。
  
  其中：第一项即为交叉熵；第二项为KL-Divergence
  $$\begin{array}{rl}KL(p,q)& =-\int p(x)\log q(x)dx+\int p(x)\log p(x)dx\\ & \\ & =\frac{1}{2}\log (2\pi {\sigma }_2^2)+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}(1+\log 2\pi {\sigma }_1^2)\\ & \\ & =\log \frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}\\ & \stackrel{q分布为\mathcal{N}(0,1)B标准正态分布}{}\log \frac{1}{{\sigma }_1}+\frac{{\sigma }_1^2+({\mu }_1-0{)}^2}{2\cdot (1{)}^2}-\frac{1}{2}\\ & =\log \frac{1}{{\sigma }_1}+\frac{{\sigma }_1^2+{\mu }_1^2}{2}-\frac{1}{2}\\ & =-\frac{1}{2}[2\log {\sigma }_1-({\sigma }_1^2+{\mu }_1^2)+1]\end{array}$$
• 它妙就妙在它为每个输入$x$, 生成了一个潜在概率分布 $p(z|x)$,然后再从分布中进行随机采样，从而得到了连续完整的潜在空间，解决了AE中无法用于生成的问题。
  
• VAE除了能让我们能够自己产生随机的潜在变量，这种约束也能提高网络的产生图片的能力。
• 但是，VAE的一个劣势就是没有使用对抗网络，所以VAE会更趋向于产生模糊的图片。

4.1 变分推断

• 变分自编码器（VAE）的想法和名字的由来便是变分推断了，那么什么是变分推断呢？
• 变分推断是MCMC搞不定场景的一种替代算法，它考虑一个贝叶斯推断问题，给定观测变量 $x\in {\mathbb{R}}^k$ 和潜变量 $z\in {\mathbb{R}}^d$，其联合概率分布为 $p(z,x)=p(z)p(x|z)$ , 目标是计算后验分布 $p(z|x)$。然后我们可以假设一个变分分布 $q(z)$ 来自分布族 $Q$，通过最小化KL散度来近似后验分布 $p(z|x)$ :
  $$\begin{array}{r}{q}^{\ast }=\underset{q(z)\in Q}{\mathrm{argmin}}KL(q(z)||p(z|x))\end{array}$$
• 这么一来，就成功的将一个贝叶斯推断问题转化为了一个优化问题~

4.2 变分推导过程

• 有了变分推断的认知，我们再回过头去看一下VAE模型的整体框架，VAE就是将AE的编码和解码过程转化为了一个贝叶斯概率模型：我们的训练数据即为观测变量 $x$， 假设它由不能直接观测到的潜变量 $z$ 生成， 于是，生成观测变量过程便是似然分布：$p(x|z)$ ，也就是解码器，因而编码器自然就是后验分布：$p(z|x)$ .
• 根据贝叶斯公式,建立先验、后验和似然的关系：
  $$p(z|x)=\frac{p(x|z)p(z)}{p(x)}={\int }_z\frac{p(x|z)p(z)}{p(x)}dz$$
• 接下来，基于上面变分推断的思想，我们假设变分分布 $q_x(z)$ , 通过最小化KL散度来近似后验分布 $p(z|x)$ ，于是，最佳的 $q_x^{\ast }$ ​便是：
  $$\begin{array}{rl}{q}_x^{\ast }& =argmin(KL(q_x(z)||p(z|x))\\ & =argmin(E_{q_x(z)}[log{q}_x(z)-logp(x|z)-logp(z)]+logp(x))\end{array}$$
• 因为训练数据 $x$ 是确定的，因此 $logp(x)$ 是一个常数，于是上面的优化问题等价于：
  $$\begin{array}{rl}{q}_x^{\ast }& =argmin(E_{q_x(z)}[log{q}_x(z)-logp(x|z)-logp(z)]\\ & =argmin(E_{q_x(z)}[-logp(x|z)+(logp(z)-log{q}_x(z))])\\ & =argmin(E_{q_x(z)}[-logp(x|z)+KL(q_x(z)||p(z))])\end{array}$$
• 此时，观察一下优化方程的形式…已经是我们前面所说的VAE的损失函数了~~
• 显然，跟我们希望解码准确的目标是一致的。要解码的准，则 $p(x|z)$ 应该尽可能的小，编码特征 $z$ 的分布 $q_x(z)$ 同 $p(z)$ 尽可能的接近，此时恰好 $-logp(x|z)$ 和 $KL(q_x(z)||p(z))$ 都尽可能的小，与损失的优化的目标也一致。

4.3 如何计算极值

• 正如前面所提到的AE潜变量的局限性，我们希望VAE的潜变量分布 $p(z)$ 应该能满足海量的输入数据 $x$ 并且相互独立，基于中心极限定理，以及为了方便采样，我们有理由直接假设 $p(z)$ 是一个标准的高斯分布 $\mathcal{N}(0,1)$ .

4.4 编码部分

• 我们先来看一下编码部分，我们希望拟合一个分布 $q_x(z)=\mathcal{N}(\mu ,\sigma )$ 尽可能接近 $p(z)=\mathcal{N}(0,1)$， 关键就在于基于输入 $x$ 计算 $\mu$ 和 $\sigma$, 直接算有点困难，于是就使用两个神经网络 $f(x)$ 和 $g(x)$ 来无脑拟合 $\mu$ 和 $\sigma$。
• 值得一提的是，很多地方实际使用的 $f(x)$、$g(x)$ 两部分神经网络并不是独立的，而是有一部分交集，即他们都先通过一个 $h(x)$ 映射到一个中间层 $h$, 然后分别对 $h$ 计算 $f(h)$ 和 $g(h)$. 这样错的好处的话一方面是可以减少参数数量，另外这样算应该会导致拟合的效果差一些，算是防止过拟合吧。

4.5 解码部分

• 解码，即从潜变量 $z$ 生成数据 $x$ 的过程，在于最大化似然 $p(x|z)$ ，那这应该是个什么分布呢？通常我们假设它是一个伯努利分布或是高斯分布。
• 知道了分布类型，那计算 $-logp(x|z)$ 最小值其实只要把分布公式带进去算就可以了.

4.5.1 高斯分布

$$\begin{array}{rl}argmin(-\log q(x|z))& =argmin\frac{1}{2}{\Vert \frac{x-\tilde{\mu }(z)}{\tilde{\sigma }(z)}\Vert }^2+\frac{c}{2}\log 2\pi +\frac{1}{2}\\ & =argmin\frac{1}{2}{\Vert \frac{x-\tilde{\mu }(z)}{\tilde{\sigma }(z)}\Vert }^2\end{array}$$

• 和预期一样，演变为了均方误差。

4.5.2 伯努利分布

• 假设伯努利的二元分布是 $P$ 和 $1-P$ (注意这里是输出没一维组成的向量)
  $$argmin(-\log q(x|z))=argmin(-x\log P-(1-x)\log (1-P))$$
• 正好就是交叉熵的损失。然后，将编码和解码部分组合到一起，就形成了完整的VAE网络。

4.6 Reparameterization trick

• 训练的时候似乎出了点问题。从编码得到的分布 $\mathcal{N}(\mu ,\sigma )$ 随机采样 $z$ 的这个过程没法求导，没法进行误差反向传播。
• Reparameterization trick ：解决VAE 的 Encoder 产生的分布函数无梯度可优化问题
  $$z=\mu +\epsilon \cdot \sigma =f(x)+\epsilon \cdot g(x),\epsilon \sim N(0,1)$$
  
• 这样一来将采样变成了一个数值变换，整个过程便可导了。
• 这样，训练好模型之后，我们可以直接将解码部分拿出来，通过标准高斯分布随机采样源源不断的生成数据了。